钢筋混凝土靶侵彻阻力模型研究进展

吴翰林,屈可朋,周 涛

(西安近代化学研究所， 西安 710065)

钢筋混凝土是现在常用的军事建筑材料。研究钢筋混凝土靶的侵彻问题可以为侵彻战斗部的设计和钢筋混凝土的配置提供一定的理论依据。钢筋混凝土的研究较素混凝土的研究的不同之处在于：加入了钢筋的混凝土的抗侵彻能力由混凝土基体和钢筋共同决定。钢筋的各类参量包括直径、网格尺寸、配筋率、配筋方式和弹体着靶点等都影响着钢筋混凝土抗侵彻的能力。复杂的参量给弹体侵彻混凝土靶的本构模型的确定造成了许多困难。

研究钢筋混凝土靶侵彻问题时，实验法、数值模拟与理论分析是最常见的3种方式。其中，理论分析是对实际复杂侵彻的问题进行假设与简化，建立相应的工程解析模型，求解微分方程组给出弹体侵彻阻力的表达式[1]。对于钢筋混凝土靶侵彻问题的理论分析，建立侵彻阻力模型是最为关键的步骤。在混凝土中加入高强度的钢筋，抗侵彻能力相对统一的素混凝土变得复杂，给侵彻过程中的力学响应分析和本构关系的确定带来不小的困难。国内外就钢筋混凝土侵彻阻力模型也开展较多的有关工作，本文就钢筋混凝土靶侵彻阻力模型对国内外的研究进展进行综述，分别分析了靶板的等效模型和基于钢筋混凝土空腔膨胀理论的侵彻阻力模型两大部分，并展望未来的研究发展方向。

1 钢筋混凝土靶等效模型

混凝土基体中添加了一定量的钢筋可以加强混凝土的力学性能，特别是抗侵彻能力。侵彻过程中，钢筋混凝土的抗侵彻强度有明显的分层现象，弹体在混凝土与钢筋混合层受到的阻力大于素混凝土层。早期的钢筋混凝土的研究手段是借鉴弹体侵彻素混凝土相关研究成果，忽略钢筋的作用或者忽略钢筋对混凝土的局部作用，从靶的整体或分层整体的角度出发，建立靶等效模型，将复杂的侵彻过程简化为侵彻素混凝土或者混凝土-钢板薄层复合材料的过程。按照上述的思路，可以将钢筋混凝土等效模型分为整体等效模型与钢筋分层等效模型。

1.1 整体等效模型

整体等效模型大部分是利用剩余速度等参数将钢筋混凝土等效为素混凝土的侵彻模型，早期国内外的学者对此做过大量的研究。有的学者直接忽略钢筋的作用，Forrestal等[2]在给出卵形弹侵彻钢筋混凝土靶的侵彻深度计算公式时，直接忽略钢筋的局部作用，将钢筋混凝土视为各向同性的材料。戴湘晖等[3]在前人的实验结论[3]的基础上，与Forrestal等[2]的研究方式类似，忽略钢筋的作用，建立弹体对钢筋混凝土薄靶的侵彻模型。部分学者通过增加混凝土的厚度来体现钢筋混凝土的抗侵彻能力。薛建锋等[4]和王茂英等[5]均采用入射速度和剩余速度均相同作为抗侵彻能力的等效依据，结合数值模拟将钢筋混凝土靶等效为具有一定厚度的素混凝土靶，研究入射速度如何影响混凝土的抗侵彻能力。另有部分学者通过增加混凝土的强度来体现钢筋混凝土的抗侵彻能力。Dancygier等[6]发现钢筋对附近的混凝土的抗拉能力的有加强效果，用增强的比例关系修正侵彻表达式。结果表明，增强比值越高，混凝土对弹体撞击的抗侵彻能力就越高。李守苍等[7]则是通过混凝土抗压强度试验[8]验证了整体等效模型的可行性：钢筋带来的钢筋混凝土抗压强度的提升与其配筋率成正比，可以将钢筋混凝土靶整体等效为强度增强的素混凝土靶。

整体等效模型将复杂的侵彻问题简化，聚焦于侵彻结果而非侵彻过程，适用于研究钢筋对混凝土整体强度的提高等问题。但整体等效模型的实质仅是素混凝土的侵彻问题，不能体现钢筋的局部约束作用。整体等效模型具体表现为两个缺点：1)当弹体直接与钢筋发生碰撞时，过载较与混凝土的碰撞更大，而此模型不能体现该过程中的力、速度等参量的变化过程；2)在钢筋的局部作用下，钢筋和混凝土复合层对弹道改变更为显著，影响的程度随靶厚的增加不断积累，而整体等效模型不能描述此累积过程。

1.2 钢筋分层等效模型

整体等效模型忽略了钢筋混凝土的非匀质性，用提升混凝土基体强度的方式等效钢筋的阻碍作用。若要研究出钢筋混凝土的非匀质性，可以采用仅等效钢筋的方式，建立钢筋分层等效模型。这类方法大部分是将钢筋层等效为一层或数层强度匹配的薄钢板，将钢筋混凝土视作素混凝土与钢板复合的材料。刘勇等[9]发现钢筋抗拉作用显著，类似于膜力，提出将钢筋层视为强度相近的钢板的等效方法。王明洋等[10]明确了等效系数，提出了钢筋网与钢板的等效计算公式

hs=1.25Aa

(1)

式中：hs为单位长度内钢板厚度，Aa为单位长度内钢筋总的横截面面积。

少部分学者未将钢筋等效为钢板层，而是将钢筋层等效为强度更高的混凝土。周宁等[11]建立卵形弹体侵彻钢筋混凝土的分层模型时，将钢筋层等效为强度更高的混凝土，其余部分按原混凝土层不作任何处理。李平[12]在研究钢筋配置方式和体积配筋率对材料力学性能的影响规律时，也是采用的相同方式，通过增加材料弹性模量和屈服强度等参数体现钢筋对混凝土的增强作用。若将素混凝土材料本构记为

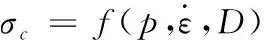
(2)

则钢筋混凝土等效本构可以记作

(3)

式中：λ为增强因子，λ=E/Ec，E和Ec分别是钢筋混凝土和素混凝土等效杨氏模量。在构建材料本构时，这种视为同类材质的等效方法，只需引入增强因子即可等效，这种方法更加方便简洁。

上述将钢筋所在层视作薄钢板或高强度混凝土的等效方法，既简化了过程又并未完全忽略过程，在一定程度上反映了侵彻过程中弹体与混凝土-钢筋碰撞时的过载特性。但是此方法不能描述实际的钢筋混凝土复杂的侵彻过程，钢筋的各项参量比如配筋率、钢筋直径，网格尺寸等对混凝土的抗侵彻能力的影响的原理也无法解释。

2 基于空腔膨胀理论的侵彻阻力模型

在混凝土的侵彻研究中，使用最广泛，也最成熟的是空腔膨胀理论。空腔膨胀理论假设侵彻造成的空腔在半无限混凝土介质中以一定速度向外膨胀，利用空穴膨胀过程传递的压缩波和空腔膨胀速度之间的关系来描述弹体侵彻过程，并由此计算出弹体加速度、速度以及侵彻深度等参量的变化。早期国内外的学者利用空腔膨胀理论对弹体侵彻素混凝土、岩石等材料建立阻力模型。比如，Forrestal等[13]和李志康等[14]研究素混凝土压力-应变的线性状态方程。图1所示的曲线为李志康、黄风雷等人的论文“高速长杆弹侵彻半无限混凝土靶的理论分析”中的曲线，他们利用Mohr-Coulomb屈服准则建立了素混凝土靶的动态空腔膨胀模型，将混凝土空腔的动态响应区两者也基本一致，划分为空腔区、压实区、开裂区、弹性区，如图2所示[14]。

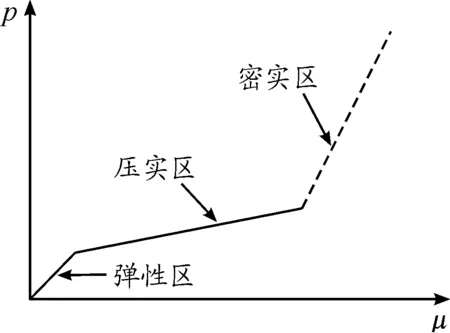
图1 压力-应变的线性状态方程曲线

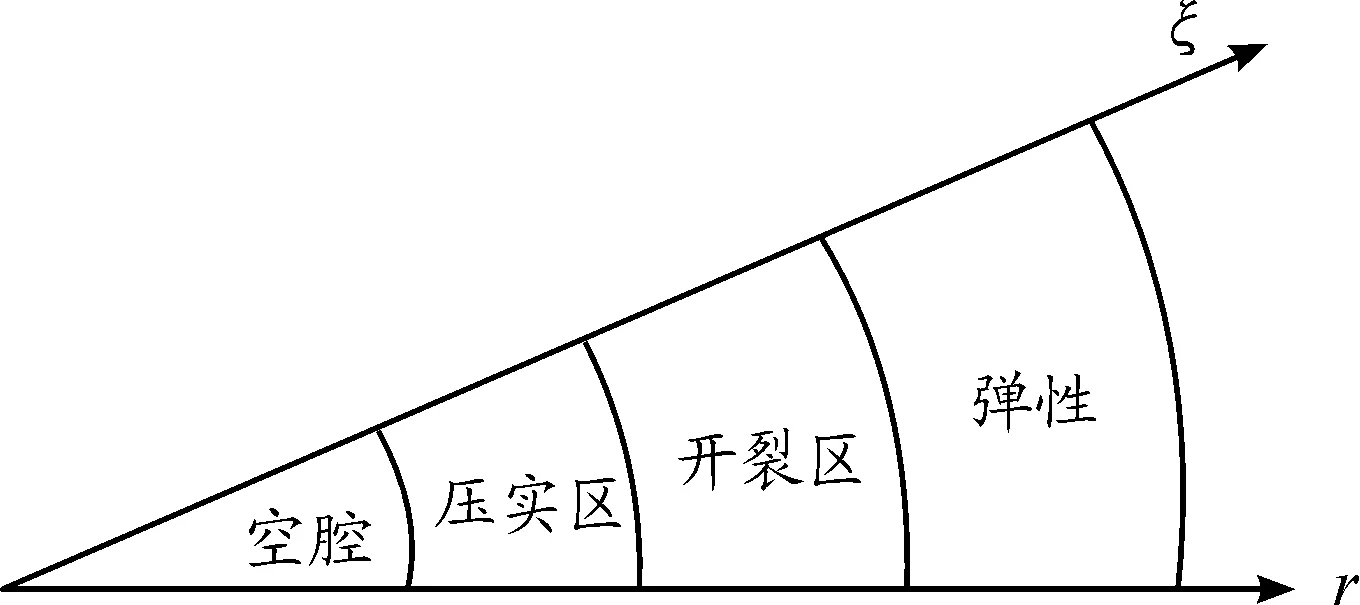
图2 动态响应区示意图

混凝土在加入钢筋后会出现额外侵彻阻力，主要从以下2个方面体现：1) 弹体侵彻过程中，钢筋扩张的形变小于混凝土扩张的形变，导致钢筋对混凝土基体起到较好的约束作用[15]，间接地增强了混凝土的侵彻阻力，这样的阻力被称为“额外间接侵彻阻力”；2) 钢筋的强度高于混凝土基体，当弹体与钢筋发生碰撞时，会消耗更多的动能，降低了弹体侵彻能力,这样的阻力被称为“额外直接侵彻阻力”。 基于空腔膨胀理论的侵彻阻力模型研究内容主要包括钢筋失效模式的选取、额外侵彻阻力和配筋参量与阻力的关系等，本文也将从这3个方面进行综述。

2.1 钢筋的失效模式

钢筋的失效模式主要有两种：1) 钢筋向内或两侧弯曲且在中段发生剪切断裂；2) 钢筋在交汇处弯曲且断裂处发生拉伸颈缩[16]。国内部分学者在建立基于空腔膨胀理论的侵彻阻力模型时仅采用上述某一种失效模式。钟大鹏[17]在建立钢筋混凝土侵彻失效准则时，提出了不考虑钢筋的剪切失效，仅考虑拉伸失效的假设，并由此推导出侵彻极限厚度和弹道极限的表达式。刘永佑等[18]在建立平头弹侵彻钢筋混凝土的阻力模型时也做了另一种的假设：将钢筋的失效模式考虑为弯曲剪切失效，忽略钢筋与弹体之间、钢筋与混凝土之间的摩擦力和拉伸失效。不少学者将两种失效模式都考虑在内。黄民荣[19]建立的侵彻钢筋混凝土的阻力模型考虑的便是弯曲剪切和拉伸断裂两种失效模式，并在后续的低中速侵彻试验中得到了验证。欧阳春等[20]考虑钢筋的两种弯曲失效，将侵彻时发生的弯曲变形简化为简支理想弹塑性梁受集中力作用的弯曲变形问题。

实际工况下，钢筋的断裂失效可能伴随着剪切断裂失效与拉伸断裂失效两种模式同时存在。判断失效模式时会存在一定的难度，目前还没有统一量化的判断方法，亟待开展后续的理论的研究。

2.2 额外侵彻阻力

确定钢筋的失效模式是建立钢筋混凝土空腔膨胀理论的必要条件。钢筋的失效模式选定后，接下来是计算钢筋对弹体的侵彻阻力。侵彻钢筋混凝土靶的阻力模型基于素混凝土靶的阻力模型的理论依据，除了需要考虑混凝土基体对弹体的阻力以外，还需要考虑前文所述两种的额外侵彻阻力：额外间接侵彻阻力和额外直接侵彻阻力。

钢筋的加入对混凝土基体起到较好的约束作用，属于间接地增强了混凝土的侵彻阻力。钟大鹏[17]通过数值模拟结果发现钢筋的主要约束效果是作用于混凝土背面，对开坑抑制效果较为明显，所以将所有的钢筋层简化等效为嵌在靶板背面的钢筋。黄民荣等[21]提出弯曲剪切断裂与弯曲拉伸断裂的侵彻阻力计算公式，若钢筋的破坏属于第一种失效模式，则阻力为

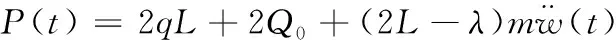
(4)

若属于第二种失效模式，则阻力为

(5)

式中：P(t)为钢筋对弹体的阻力，q为混凝土塑性流动时单位长度的极限压力，2L为梁的宽度，Q0为钢筋的塑性极限剪力，λ为已变形长度，m为单位长度质量，w(t)为钢筋的位移，N0为钢筋的塑性极限轴力，θ为固支端面的转角。

Zhang等[22]探究了钢筋对间接侵彻阻力的影响机理，发现约束作用来自于钢筋和混凝土在交界面处的粘结特性。在粘结作用下应力高效传递，弹体在未直接碰撞钢筋时也会受到额外的间接侵彻阻力作用。Deng等[23]就考虑钢筋产生的周向约束效应，用阻尼函数来描述单层钢筋对周围混凝土的约束作用，建立起钢筋混凝土靶的动态球腔膨胀模型，得到钢筋混凝土中径向应力的计算公式和理论解。张凡等[24]采用弹塑性不可压缩介质中的球腔膨胀模型来分析靶体对弹体侵彻的间接阻力作用，将钢板-钢纤维钢筋混凝土的间接阻力作用归纳为：钢纤维的增韧作用和钢板薄膜力作用。大部分研究思路均是基于传统球腔膨胀模型，部分学者修改了球腔膨胀模型的分区，在原有的分区基础上，加入了因引入钢筋而形成的特殊响应区。比如，张欣欣等[25]在素混凝土空腔膨胀模型的开裂区与密实区之间加入扩容区，建立含有钢筋的空腔膨胀模型，最后结合试验也证实钢筋对混凝土约束作用的存在。

上述的研究未考虑钢筋直接碰撞作用，参考素混凝土靶空腔膨胀理论，根据靶的形变程度将靶板划分成响应区，结合相邻分区的Hugoniot跳跃条件、材料本构方程、分区边界条件等，解出质量和动量守恒方程。但钢筋影响弹体侵彻过程的因素众多，而该理论仅反映了钢筋带来的间接作用，钢筋对弹体直接碰撞的过程有待进一步研究。

钢筋的强度高于混凝土基体，当弹体与钢筋发生碰撞时，会消耗更多的动能，降低了弹体侵彻能力。考虑钢筋直接碰撞作用的侵彻阻力模型就是将额外直接侵彻阻力的影响考虑在内的理论模型。弹体与钢筋直接碰撞的着靶点可以分为四种：钢筋网中心点，钢筋交汇点、单根钢筋中点和其他任意着靶点。大部分学者就前三种特殊着靶点进行研究，通过建立空腔膨胀理论，确定钢筋的各种参量与额外直接侵彻阻力的关系。通过弹体与钢筋在交汇处直接碰撞的试验[26]，发现钢筋直径和网格尺寸对侵彻深度的影响较大，间接证明钢筋直径和网格尺寸在直接碰撞的情况下为影响侵彻阻力的主要因素。刘志林等[27]考虑钢筋对弹体的直接阻力作用，应用空腔膨胀理论模型计算混凝土对弹体的侵彻阻力，分析了钢筋直径、网层间距以及撞击点位置对侵彻的影响。可以看出，钢筋直径、网格尺寸、网层间距及撞击点位置等配筋参数均会影响直接侵彻阻力。欧阳春等[8,20]简化弹体与钢筋的接触方式为点接触，将弹体与钢筋的碰撞问题转换为接触点在阻尼介质中受冲击荷载作用的动力响应问题。周宁等[11,28]提出更为全面的侵彻工程解析模型，同时考虑了侵彻过程中受到的直接碰撞作用与动静阻力，将钢筋产生的弯曲变形的过程简化为不必分析整个钢筋的动力响应的简支理想弹塑性梁受集中力作用的弯曲变形问题，提出在任意t时刻，单位长度钢筋对弹体的侵彻阻力为

(6)

式中：ρ为钢筋密度;d为钢筋直径，其他字母在前文中已作说明。

张爽等[29]结合钢筋的受力情况和失效模式，得到单根钢筋在弹体不同的着靶点的碰撞作用下的动态响应，最后类推得到弹体与单层或双层多根钢筋碰撞的响应规律，建立全面完整的钢筋混凝土靶侵彻阻力模型。但该模型未考虑钢筋网格的尺寸对阻力的影响，有待进一步研究。解决弹体直接碰撞钢筋的侵彻阻力问题的核心是解决单根钢筋受冲击荷载作用的动力响应问题。

建立考虑钢筋直接碰撞作用的侵彻阻力模型，可以反映各类配筋参数对钢筋混凝土靶侵彻过程中的抗侵彻能力的影响规律。弹体与钢筋直接碰撞的阻力模型研究目前存在3个的问题：1) 现有的试验设备与测量技术无法测试钢筋对弹体直接碰撞的作用力，上述模型不能很好地通过实弹试验进行验证。2) 对任意着靶点的研究较少，研究主要集中在钢筋网中心点，钢筋交汇点、单根钢筋中点。3) 着靶点的控制精度较为粗糙，研究特殊着靶点的实验易出现着靶位置偏差。

2.3 配筋参量与阻力的关系

如今的研究热点聚焦于将钢筋作用局限化，利用空腔膨胀理论解决钢筋的额外阻力，通过改变配筋参量，对比钢筋混凝土靶的抗侵彻能力的变化，得到对应的影响规律。配筋参量包括有钢筋直径、网格尺寸和弹体着靶点以外，还有配筋率和配筋方式，下面主要对这两类配筋参量进行综述。

Zhang等[22]以改进过的Griffith屈服准则为本构模型，进行了动态球腔膨胀分析，计算了不同重量的弹体在不同配筋率的钢筋混凝土靶中侵彻的实验，分析侵彻深度和速度等参数与配筋率的关系。邓勇军等[15]改进了钢筋混凝土空腔膨胀的理论模型，与Forrestal素混凝土模型不同之处在于：多出能反映钢筋对径向应力与速度的影响的两项代数式，这两项均与配筋率有关。牛振坤[30]则是细分了空腔膨胀的响应分区，得到随着配筋率的增加，破裂区和粉碎区的膨胀速度减小，径向应力显著增大的结论。楼建锋等[31]通过调整钢筋直径的大小改变体积配筋率，发现在弹体直径大于钢筋间距的情况时，钢筋越粗，含筋率越高，钢筋混凝土靶板的抗侵彻能力越强。配筋率是一项重要的配筋参数，影响着径向应力、侵彻深度和膨胀速度。对配筋率如何影响侵彻能力的研究是当今的热点之一，但改变钢筋直径、网层间距等参量会改变配筋率，如何解耦配筋率与其他因素是需要解决的问题。

上述研究涉及的是配筋率，不同配筋方式对侵彻阻力的影响同样不可忽略。通过落锤冲击钢筋混凝土实验[32]，发现在低速侵彻配筋率相同的混凝土靶时，钢筋排布方式影响着裂纹形式和失效模式的确定。对比实验[33]表明，在配筋率和靶板强度相近的前提下，配筋直径更小的钢丝网水泥靶比钢筋混凝土靶的抗侵彻能力更强，靶板损伤区域和破碎崩落的总质量更小。楼建锋等[31]通过调整钢筋排列的疏密进行侵彻对比试验，发现配筋率相同配筋方式不同的钢筋混凝土靶板将对弹体产生不同的侵彻阻力。配筋方式更多影响的是裂纹损伤的情况，配筋方式涉及的变化较多，值得更深入的探究。

目前基于空腔膨胀理论的侵彻阻力模型均是考虑钢筋的作用的前提下，探究配筋参量(钢筋直径、网格尺寸、配筋率、配筋方式和弹体着靶点等)对侵彻阻力(间接侵彻阻力与直接侵彻阻力)的影响规律。但现有的大部分理论模型结论是在垂直正侵彻的工况下得出，是否可以推广到更一般的斜侵彻值得进一步论证。同时，现有的理论模型的侵彻对象主要是半无限厚靶，弹体侵彻钢筋混凝土有限厚靶甚至薄靶时，还应考虑靶板侧面、背面的自由面效应[34-35]，空腔膨胀理论分区的修正等问题。

3 其他相关理论

除了上述两大类侵彻阻力模型外，部分学者还开展了侵彻钢筋混凝土靶的其他理论研究。

有的学者针对厚度方向的开裂情况或者靶板边界及背部等的影响进行研究。咸玉席等[36]就厚度方向开裂破坏问题建立二阶段模型，并确定钢筋混凝土靶板破坏模式发生转换的条件和能量临界的求解方程。张学伦等[34]和薛建锋等[35]通过侵彻深度分别判断靶板侧边界效应和自由边界对侵彻能力的影响。李江涛等[37]强调侵彻薄靶时会在其背面产生截锥形的塞块，同时给出了塞块的几何参数的关系式。有的学者建立了新的侵彻模型或者提出了新的计算侵彻阻力函数等。Chen等[38]提出钢筋混凝土靶常规侵彻的弹道性能的显式方程，引入钢筋无量纲参数，直接研究配筋率和钢筋抗拉强度对侵彻的影响。杨青顺[39]采用统一强度理论作为混凝土的破坏准则，求得弹塑性响应的空腔膨胀压力与侵彻深度。何翔等[40]采用抗侵彻系数描述在相同着靶速度的条件下侵彻混凝土和钢筋混凝土的深度的区别，并编写了相应的计算程序，推广到斜侵彻问题。王德荣等[41]将在低速撞击下的混凝土板的归一化临界震塌与贯穿厚度归纳为冲击因子、钢筋抗力系数和弹头形状等参量相关的函数，利用极限理论和滑移线场理论，提出阻力上限计算方法。无论其他相关理论的研究方法与角度如何不同，最终都是在解决复杂的钢筋混凝土参量与其抗侵彻能力的影响关系。

4 结论

1) 现有的理论模型对弹体直接碰撞钢筋的着靶位置的划分较为理想化，几乎都是分为钢筋网格中心点、钢筋交汇点与单根钢筋中点，对更一般的任意位置研究较少，对任意位置的侵彻阻力的规律也无文献提及。

2) 现有的试验设备控制着靶点的精确程度不高，导致特殊位置的着靶点的侵彻实验存在较大偏差。同时，对弹体所受的侵彻阻力进行直接测量也较为困难，需要更先进的试验设备和测试技术。

3) 目前研究的弹体侵彻速度偏低，弹体被视为刚体。经过高速侵彻后，弹坑中发现大量融化后又结晶的金属碎末，表明弹体已进入半流体侵彻阶段。一旦发生半流体侵蚀或流体侵蚀时，弹体的质量损失率将大大增加，弹体头部甚至整个弹体的形状无法保持原状，侵彻阻力的变化更加难以确定。有关高速/超高速侵彻时发生的质量侵蚀与侵彻阻力的关系的理论研究较少。