基于改进Merkle-Tree认证方法的可验证多关键词搜索方案

田有亮，骆琴

（1.公共大数据国家重点实验室（贵州大学），贵州 贵阳 550025；2.贵州大学计算机科学与技术学院，贵州 贵阳 550025；3.贵州大学密码学与数据安全研究所，贵州 贵阳 550025；4.贵州大学数学与统计学院，贵州 贵阳 550025）

1 引言

随着大数据的开放与共享，数据搜索结果的可验证性显得尤其重要。搜索结果的可验证性是指用户能够高效地对服务器返回的搜索结果进行认证。现有可搜索加密方案中的结果验证方法普遍存在成本高、效率低等问题，为实现多关键词搜索结果高效验证和安全性需求带来了巨大挑战。

可搜索加密的目的是解决云存储[1-3]条件下密文的高效搜索问题，一个安全的可搜索加密方案可以使云服务器在不知道用户明文数据信息的情况下，实现对密文的搜索。最早由Song等[4]提出的方案使用对称加密算法对文档中的每个单词进行加密，搜索时对关键词也同样加密，然后通过全文扫描，将加密的搜索关键词与加密的文档进行比对，匹配到具有相同密文单词的文件则是用户想要的文件。但是这种方法检索的效率较低，耗时较多。Goh[5]基于“文件-关键词”的思想，通过利用布隆过滤器来建立文件索引，对每个文件包含的关键词使用伪随机函数映射到该文件的布隆过滤器索引中，搜索时提交查询陷门，根据每个文件的索引判断该文件是否包含特定的查询关键词。这种建立安全索引的方法使搜索效率得到了显著提高，但云服务器需要与用户进行两次交互才能完成搜索，增加了用户的通信开销。Chang等[6]利用随机比特建立

关键词的索引，并在搜索时通过恢复索引的部分信息来匹配关键词。Curtmola等[7]提出了在整个文件集合上建立加密关键词的Hash索引，搜索令牌由

关键词陷门和文件拥有者的身份信息组成，可以通过关键词陷门与关键词密文的匹配来产生搜索结果，最初的研究者只关注单关键词搜索方案的实现。

考虑到单关键词不能精准定位到用户想要的文件，Golle等[8]提出2个连接关键词搜索方案。该方案假设对每次搜索的每个文件都有固定数量的关键词域，第一个方案需要为每个文件进行两次模幂运算，其陷门的大小与加密文件的总数成线性关系。第二个方案虽然使陷门的大小固定，但是却与关键词域的数量成正比。而且第二个方案的存储开销是第一个方案的两倍。Zheng等[9]提出加密数据的无证书关键词搜索（CLKS,certificateless keyword search on encrypted data）方案，该方案不仅支持对加密数据进行多关键词搜索，而且由于无证书加密技术避免了证书管理问题，但通信开销比较大。Zhang等[10]提出了一种排序的多关键词搜索方案，该方案支持在多所有者模型中进行结果相关性排序搜索，降低了返回所有搜索结果的需要，但不能对恶意云服务器返回的虚假搜索结果进行验证。

因此，应使用某种验证方法来确保用户搜索结果的正确性[11-12]。Sun等[13]提出了一种有效的基于树的索引结构来实现真实性验证。Wang等[14]提出了一个完全实现查询完整性验证的方案，该方案利用布隆过滤器[15]、MHT（Merkle Hash Tree）等数据结构，借助伪随机置换、哈希函数等工具来验证查询完整性。但该方案只适用于静态数据库，不支持数据库的动态更新。文献[16]提出了一种可验证的多关键词搜索方案，该方案借助私人审计服务器来验证搜索结果的正确性，但也不能实现动态性。考虑到用户需要经常更新存储到云端的数据，支持动态操作的可搜索加密方案[17-20]得到研究者们的广泛研究。Kurosawa[21]演示了如何以验证的方式支持文档的更新操作，以及检测恶意云服务器的攻击行为。

在传统的有效验证方案中，用户需要委托第三方来验证搜索结果，此方法虽然保证了搜索结果的正确性，但是增加了计算和通信开销。针对上述问题，本文采用文献[16]所提的验证思想，基于改进的Merkle-Tree认证方法[22]提出搜索结果高效验证的多关键词搜索方案，主要贡献如下。

1)在搜索阶段，基于Miao等[16]提出的（VMKS,verifiable multiple keywords search）方案构造多关键词的可搜索算法，实现高效精准的多关键词搜索，并且通过方案分析，证明其可行性。

2)在认证阶段，利用改进的Merkle-Tree认证方法构造搜索方案的验证及动态更新算法，实现高效认证和动态更新；与经典的MHT相比，计算成本从O(n)降低到O(logn)。

3)对所提方案的正确性、安全性和性能进行了详细证明与分析，并在决策线性假设和CDH（computational Diffie-Hellman）假设下证明所提方案满足密文不可区分性和不可伪造性。

2 预备知识

BLS（Boneh-Lynn-Shacham）短签名由文献[23]定义，它是用于消息签名的身份验证，使用双线性对[16]进行签名身份认证。与本文方案安全性相关的安全假设描述如下。

定义1CDH假设。假设G是阶为p的乘法循环群，g是G的生成元，给定三元组g,ga,gb∈G，且随机选择2个元素，对于任何概率多项式时间的敌手A，以不可忽略的优势ε，计算gab∈G是不可行的，其中A的优势满足

定义2决策线性假设。假设G是阶为p的群，g是G的生成元，给定元组和，其中u,v,l∈G，概率多项式时间敌手A的主要目标是区分与在群G里的随机元素l，如果A在打破DL（decisional linear）问题上的优势可以忽略不计，其优势定义为

2.1 经典的MHT

MHT是著名的二叉树数据结构，其中除叶子节点外的每个节点都是其叶子节点的串联，顶部的节点称为根节点。MHT中的叶子节点表示数据块的哈希值，根节点的身份验证可确保所有节点的完整性。图1描述了具有8个叶子节点的MHT，如果要对h(f[3])处的数据节点进行完整性验证，则需要知道辅助信息（AI,auxiliary information）和AI(f[3]):{(hC,L),h(f[3]),(h(f[4]),R),(hB,R)}，为了验证数据块f[3]的完整性，认证者执行以下操作。

1)计算hD←(h(f[3])||h(f[4]))。

2)计算hA←(hC||hD)。

3)计算根hR←(hA,hB)。

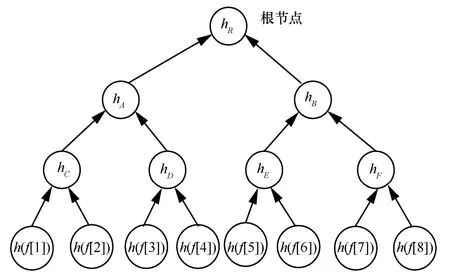
图1 经典的MHT

2.2 改进的Merkle-Tree认证方法

为了降低在运用MHT验证过程中节点搜索的计算成本，本文结合文献[22]改进的Merkle-Tree认证方法，将计算成本从经典的MHT的O(n)降低到O(logn)，树的每个节点都有2个信息：一个是数据块的哈希值；另一个是相对索引。与节点T关联的相对索引是指属于T的子树的叶子节点的数量，叶子节点的相对索引值设置为1。例如，如果L和R是左右子节点，其哈希值分别为ha和hb，相对索引字段分别为父节点T的ra和rb，则节点T的哈希值为(ha||hb)且相对索引字段值为(ra+rb)。时间戳字段与树的根节点串联，该时间戳是与根哈希值串联的树创建的日期和时间。改进的Merkle-Tree如图2所示，有hR:(hA||hB||dt)，其中dt是Merkle-Tree创建的日期和时间。由于hR总是针对树中任何数据块做任何修改而更新，因此最后修改的日期和时间会反映在hR，从而确保了数据的新鲜度。

图2 改进的Merkle-Tree

3 问题描述

3.1 方案模型

如图3所示，模型中有4个实体，即密钥生成中心（KGC,key generation center）、数据拥有者（DO,data owner）、用户（DU,data user）以及云服务器（CSP,cloud service provider）。首先，KGC根据用户相应标识生成部分私钥，其余部分私钥由用户自己生成。其次，DO先对文件加密并为文件创建索引，将文件F分割成n个数据块(f[1],f[2],…,f[n])，数据块f[i]作为Merkle-Tree的叶子节点生成完整的树并对根进行签名，然后将这些发送给CSP存储。DU按照自己的需求向服务器提交相应的查询陷门，CSP根据每个文件的索引判断该文件是否包含特定的查询关键词搜索匹配的结果。当用户收到服务器返回的结果时，向服务器提出质询消息验证结果的完整性。

图3 方案模型

3.2 方案定义

本文方案由以下7个算法组成。

1)GlobalSetup(λ)。输入安全参数λ，发布公共参数，保存主密钥，输出系统公共参数param和主密钥msk。

2)ParKeyGen(msk,ID)。给定用户ID，KGC运行该算法并为用户ID返回相应的部分私钥pskID=(psk1,psk2)。

3)KeyGen(param,pskID,ID,msk)。输入msk、ID、param、pskID，最后为用户输出公私钥(pk,sk)。

4）Encrypt(F,W,pk,pskID,ID)。给出数据文件集F和关键词集W，DO执行该算法，输出密文集CT、索引集I、文件标签τ和签名集δ，DO将这些元组(CT,I,τ,δ)上传至CSP中存储。

5)Trapdoor(sk,pkID,W',pk,ID)。输入搜索查询W'，用户DO执行该算法，生成搜索令牌TW'并发送给CSP。

6)Search(pk,TW',I,CT)。CSP收到用户的搜索请求后，搜索与关键词陷门TW'匹配的索引I的相关文件CT'及其相应的身份标识ID'，然后将(CT',ID')发送给用户。

7)Verify(CT',pk,ρ)。用户收到搜索结果CT'，向服务器提交质询消息，服务器返回相应的辅助消息，验证结果的完整性，如果CT'通过认证算法，用户输出1；否则，输出0。

3.3 安全模型

与方案[16,24]相似，本文首先假设CSP是半诚实且好奇的，这意味着它将诚实地执行算法，但会尝试学习尽可能多的私有信息。其次，假设不能完全信任KGC，那么KGC诚实地遵循算法规定，但可能会尝试使用其获得的信息来渗透更多的信息。本文考虑2种类型的敌手，即A1和A2。A1表示外部攻击者，除了主密钥msk以外允许控制用户ID的公钥；A2表示内部攻击者，可以访问主密钥KGC，而不需要控制用户ID的公钥。

本文通过下面的2个安全游戏来说明本文方案对以上2种不利因素都是安全的。设A1为Game1中的敌手，A2为Game2中的敌手，C是维护下面2个列表的挑战者。

Tlist：用于存储元组(ID,W)，这就意味着与用户ID的关键词W相关的搜索令牌已被(A1,A2)查询。

Ulist：用于存储元组(ID,psk,sk,pk,ϖ1,ϖ2,ϖ3)，ϖ1=1表示psk被(A1,A2)查询；否则，表示未被查询。同样地，ϖ2=1和ϖ3=1表示sk,pk被(A1,A2)查询；否则，表示敌手不会查询sk,pk。具体来说，本文的安全游戏是在敌手A1和挑战者C之间进行的。

初始化。挑战者运行GlobalSetup，输出公共参数param和主密钥msk，把公共参数param发送给敌手A1，并且设置列表为空。

阶段1。假设A1可以在多项式时间查询以下预言机，则C可以执行以下算法。

ParKeyGen。给定来自A1的用户标识ID，在Ulist中的psk不为空，C返回psk；否则，挑战者利用主密钥msk执行ParKeyGen算法以获得psk，将元组(ID,psk,*,*,1,0,0)添加到列表Ulist中，并将psk发送给A1，其中符号“*”表示为空。

KeyGen。给定A1的ID，如果sk不为空，则挑战者从Ulist中选择sk；如果psk在Ulist中不为空，则挑战者调用ParKeyGen算法利用psk生成sk，然后挑战者在Ulist中添加sk。假设上面2种情况都不成立，则C执行ParKeyGen和KeyGen算法获得psk和sk。然后，C在Ulist中添加元组(ID,psk,sk)。最后，C更新与用户ID关联的Ulist中的ϖ1=1，ϖ2=1并将sk发送给A1。

Ulist中的pk不为空，那么挑战者检索pk；如果Ulist中的sk不为空，则检索sk且挑战者运行KeyGen以输出pk并将其添加到与ID有关的Ulist中。

如果Ulist中的psk不为空，则C将检索psk，运行KeyGen生成sk和pk，并将sk、pk添加到Ulist中。

否则，C将同时运行ParKeyGen和KeyGen算法以生成psk、sk和pk，并将元组(ID,psk,sk,pk,0,0,0)添加到Ulist中，C将pk发送给A1。

Rplace-pk。给定用户ID和来自A1的替换公钥pk，C将Ulist中的pk更新为pk'，并针对ID设置ϖ3=1。

Trapdoor。给定用户ID和A1的关键词W，挑战者在Ulist中检索sk，执行Trapdoor算法，将元组(ID,W)添加到Tlist中，然后将陷门发送给A1。

挑战阶段。A1提交2个相同长度的不同关键词W0,W1以及用户ID。给定Ulist中的(ID*,psk*,sk*,ϖ1,ϖ2,ϖ3)，如果ϖ1=0，ϖ2=0，仍然要求psk*和sk*不能被A1查询。此外，(ID*,W0)和(ID*,W1)都没有存储在Tlist中。如果ϖ3=0则可以替换pk*，否则无法替换。C选择一个随机位λ∈(0,1)，通过运行Encrypt算法对Wλ进行加密并将密文I*返回给A1。

阶段2。该阶段与阶段1相似，唯一的限制是不能进行以下查询：A1不能查询ParKeyGen(ID*)、KeyGen(ID*)、Trapdoor(ID*,W0)或者Trapdoor(ID*,W1)。

猜测。A1输出为λ*，A1赢得游戏的条件是λ*=λ。

定义3对于任何概率多项式时间的算法A1，能以不可忽略的优势赢得Game1，则实现了针对A1的密文不可区分性。

4 方案构造

本节介绍方案的具体构造。首先，基于Miao等[16]提出的VMKS方案构造多关键词的可搜索算法，实现高效精准的多关键词搜索。其次，利用改进的Merkle-Tree认证方法构造搜索方案的验证及动态更新算法，防止数据篡改、删除和伪造等不法操作的高效验证，且时间戳与根节点的连接确保了数据的新鲜度，这是文献[16]没有的特点，具体算法如下。

4.1 初始化

GlobalSetup(λ)。输入安全参数λ，假设e:G×G→GT是双线性映射，G是生成元为g、阶数为p的一个群，KGC选择随机元素u,u1,…,un∈G，并且计算gx,gy，最后，选择2个哈希函数并且定义一个哈希函数，其中ID={ID1,ID2,…,IDn}，此外，KGC生成公私钥对(pk,sk)。系统公共参数param={g,h,H0,H1,g0,u,u1,…,un,gx,gy}，主密钥msk={x,y}，将系统参数param发布出来，msk由KGC自己保存。

4.2 密钥生成

密钥生成分为2个步骤。首先，KGC在ParKeyGen算法中为用户ID生成部分私钥；其次，用户ID在KeyGen算法中为自己生成最终的私钥。

1)ParKeyGen(msk,ID)。给出特定用户DU的身份ID，KGC选取随机元素，计算并将其通过安全通道发送给用户DU，则它的部分私钥为pskID=(psk1,psk2)。

2)KeyGen(param,pskID,ID,msk)。DU随机选取2个元素并且计算DU的公私钥对为

4.3 密文生成

DO将存储在服务器中的数据文件F分割成n个数据块(f[1],f[2],…,f[n])，并在上传之前对其加密，具体算法如下。

1)FileTagGen(fname,t,n,dt)。由DO执行该算法，为文件F生成标签，选择随机元素μ∈G，生成系统日期和时间，记为dt，系统日期和时间连接在文件标签τ后，确保文件的新鲜度，使π=(fname||n||μ||dt)，其中π∈G且τ=sigt(π)是文件F的标签，连接的字符串π被存储在本地是为了以后对文件标签的验证。

2)BlockSigGen(t,h(f[i]),dt,μ)。生成文件标签之后，DO每个文件块f[i]生成的BLS签名为ϕi=(h(f[i])μf[i])t，i∈{1,2,…,n}，签名集为δ={ϕi},1≤i≤n，DO用h(f[i])作为叶子节点生成树，其中，根节点hR是与系统日期和时间连接的，即hR=hR||dt，根的签名为ρ←(hR)t。

3)Encrypt(F,W,pk,pskID,ID)。DO从文件f[i]中提取关键词集Wi⊆W={w1,…,wn}并为这些文件创建索引Ii。DO选择2个随机数并且计算，最后，DO将{I,C,τ,δ,ρ}和相应的身份标识ID={ID1,…,IDd}上传给CSP。

4.4 陷门生成

用户想要搜索感兴趣的文件，需要将关键词加密向CSP请求查询，CSP收到相应的查询陷门执行搜索算法。

Trapdoor(sk,pkID,W',pk,ID)。给定查询的关键词集，用户DU选择元素s∈Zp，然后计算陷门TW'={T1,T2,T3,T4}，其中，

4.5 密文搜索

根据用户提交的相应查询陷门，CSP执行搜索算法，搜索与陷门匹配的结果。

Search(pk,TW',I,C)。收到陷门TW'之后，CSP计算三元组(σ1,σ2,σ3)，其中σ1=e(I2,T3)，CSP通过判断式(1)是否成立，来匹配陷门TW'和索引I，最后，返回相关的密文

4.6 结果认证

Verify(C′,pk,ρ)。用户收到结果C'时，向CSP提出质询消息返回相应辅助消息来验证C'的正确性，用户首先选择k个元素集Q={ς1,…,ςk},k∈[1,n]且∀i∈Q，其次选择一个随机元素bi∈Zp，最后，发送质询消息M←(i,bi)i∈Q给CSP。

2)用户对文件标签及根签名进行验证，当用户收到CSP回应的证明信息时，则需要计算以下3个式子来验证结果的正确性。

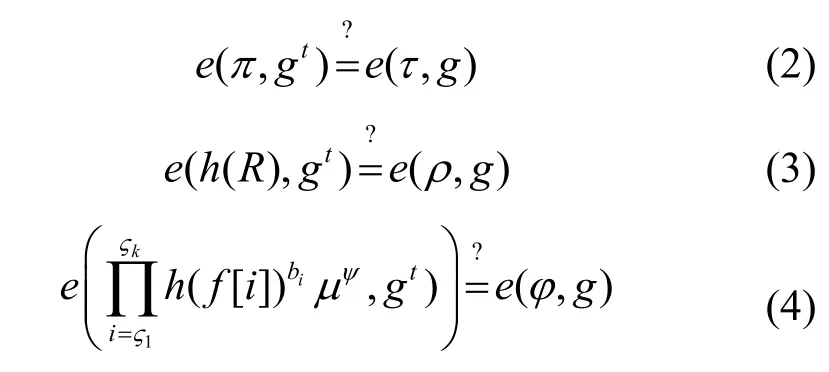
5 动态更新

允许数据动态过程是可搜索加密方案中数据完整性查询的一个重要特性。但是，现有的大多数方案都没有这个特性，本文将介绍利用改进的Merkle-Tree认证方法构造搜索方案的动态更新算法。

5.1 数据修改

DO向服务器发出请求，并按以下方式对数据进行修改。

首先，DO为新的文件生成标签ϕ'=(h(f[i]')μf[i]')t。

接下来，DO生成新的文件标签τ'←sigk(fname||n||μ||dt)，来验证修改的日期和时间，以确保数据的新鲜度。

数据修改的框架为(X,i,f[i]',h(f[i]'),ϕ',τ')，将这些信息传送给CSP，其中X表示修改操作，i表示要修改的数据块。收到以上消息后，CSP将执行以下替换：首先，用替换fi；其次，分别用φ'和τ′替换φ和τ；最后，用h(f[i]')替换h(f[i])。最终，CSP生成新的根哈希值R'并用h(f[i]')进行Merkle-Tree重建，CSP将修改过程的证明提供给数据拥有者进行验证，即Pf={ϕ,(h(f[i]),AI(i)),ρ,SIB(i),R'}，数据拥有者从CSP收到数据修改证明后，首先验证τ，其次通过式(3)使用{h(f[i]'),AI(i))i,ρ}验证根。如果认证成功，数据拥有者使用{h(f[i]'),AI(i))i}计算新生成的根并且将其与R'进行比较，若比较成功，数据拥有者通过签名私钥t认证R'，因此生成根的签名ρ'=h(R')t，并把它发送到CSP存储。最后，DO为新的数据块运行验证算法，如果结果为真，DO可以从本地删除{f[i]',τ',ρ'}。

5.2 数据添加

若DO想在一个特殊的位置添加一个数据块f*，则按以下操作执行。

首先，为新的数据块生成签名ϕ*=(h(f*)μf*))t。

其次，生成新的文件标签τ*←sigt(fname||n||μ||dt)。若DO插入（如图4所示）的数据消息为(I,V,i,f*,ϕ',τ')，其中，I表示数据插入，字段V表示要插入的新块的位置，V←A表示第i个位置之后的插入，V←B表示第i个位置之前的插入，并且把这些消息发送到CSP，收到消息后，CSP保存f*和对应的叶子节点h(f*)，CSP在Merkle-Tree中找到h(f[i])并保留AI(i)插入叶子节点h(f*)，如果将字段V设置为A，则具有哈希值(h(f[i])||h(f*))的内部节点将被连接到原始树中；如果将字段V设置为B，将具有哈希值(h(f*)||h(f[i]))的内部节点添加到索引设置为2的原始树中。

最后，CSP修改从第i个节点到最高节点（根节点）的路径上每个节点的详细信息。由于重新生成了Merkle-Tree，CSP产生了一个新的根R并且为DO提供了插入操作的证明消息，表示为Pf={ϕ,(h(f[i]),AI(i)),SIB(i),ρ,R'}，其中AI(i)表示先前树中f[i]的辅助信息。在收到插入过程的证明时，DO首先验证τ，验证成功后，使用{h(f[i]),AI(i)}产生根，然后通过式(3)验证这个新生成的根，如果式(3)成立，那么DO可以验证CSP是否正确地完成了文件插入过程，从而使用{h(f[i]),AI(i)，,h(f*)}生成新的根并与R'进行比较，若结果成功，DO将R'的认证(h(R'))t发送给CSP更新。最后，DO为新的数据块运行认证算法，如果结果为真，数据拥有者就可以从本地存储中移除{ρ',f*,τ'}。

6 方案分析

6.1 正确性分析

为了实现方案的安全性，本文必须保证CSP能够诚实地执行密文检索操作，通过验证式(1)和式(4)的成立，确定没有篡改结果。

对于式(1)，有

如果W'⊆W，有σ1=σ2σ3，因此式(1)成立，对搜索结果的完整性验证则需要验证式(4)的正确性。

则有式(4)成立，因此本文方案是正确的。

图4 数据添加

6.2 安全性分析

在决策线性假设和CDH假设下，实现了密文不可区分性和签名的不可伪造性，半诚实且好奇的CSP无法伪造有效的证明信息。通过利用与文献[22]方案相同的安全游戏实现安全目标。本文通过以下定理来保证本文方案的安全性。

定理1假设第1型敌手最多ξ1次查询预言机ParKeyGen，ξ2次查询预言机KeyGen，表示敌手A打破哈希函数H0的优势，AdvDL(λ)表示敌手A打破DL假设的优势，则第1型敌手打破密文不可区分性的优势为

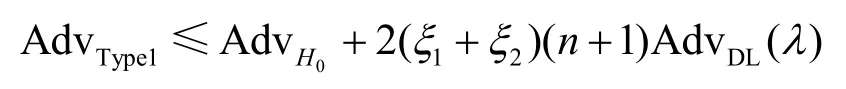
证明设Si表示敌手A想要赢得游戏i的事件，Advi表示敌手A的优势。假设除了预定义的事件EP发生，i+1轮游戏终止并输出一个随机位外，i+1轮游戏与i轮游戏执行相同的操作。如果EP是不可忽略的且它独立于Si，则有

接下来，本文将展示一系列安全游戏模拟。

Game1。在该轮游戏中，敌手A按照Game1中定义的步骤执行，即挑战者C生成主密钥、公共参数和用户部分私钥。令是挑战阶段用户的身份和公钥，是返回给敌手A的密文。

Game2。在该轮游戏中，A继续执行Game1中定义的步骤，除了H0是一个抗碰撞的哈希函数外，有

Game3。在该轮游戏中，除了生成的公共参数外，C执行的游戏与Game2相同。

1)C选择和ηu∈{0,…,p}，使ηu(n+1)＜p。

2)C选择其中Kuj∈Zηu,1≤j≤n。

3)C选择其中Tuj∈Zηu,1≤j≤n。

公共参数设置为

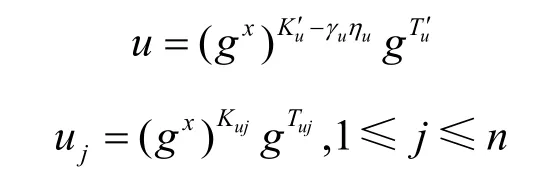
可以看到，生成过程中并没有改变公共参数，因此，有Pr[S3]=Pr[S2]且Adv3=Adv2。

Game4。在该轮游戏中，除了猜测阶段，C执行的游戏与Game3相同，其中C为输入ID=ID1,…,IDn。定义2个函数分别为

在猜测阶段，C检查Au(ID*)是否等于零，如果为零，则C终止并且输出b'∈{0,1}作为A的猜测；否则，C执行与Game3相同的步骤。

Game5。在该轮游戏中，除了猜测阶段，C执行的游戏与Game4相同，C检查以下2种情况是否发生。

1)对于身份ID，Au(ID)=0且对ParKeyGen预言机进行查询。

2)对于身份ID，Au(ID)=0且对KeyGen预言机进行查询。

如果以上2种情况发生了，则C终止并且输出b'∈{0,1}作为A的猜测，由于上述情况的发生不独立于Game4，则本文将估计Pr[¬E5]的下确界，即

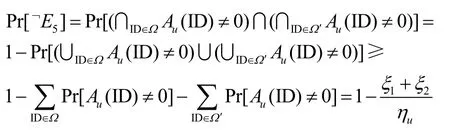
其中，Ω表示用户ID查询预言机ParKeyGen的集合，Ω′表示用户ID查询预言机KeyGen的集合，ξ1表示查询预言机ParKeyGen的次数，ξ2表示查询预言机KeyGen的次数。

如果ηu=2(ξ1+ξ2)，则因此，

Game6。在该轮游戏中，除了使用gx,gy作为公钥外，其中x,y是C不知道的，C执行的游戏与Game5相同；除了预言机ParKeyGen，C根据算法规范处理预言机。

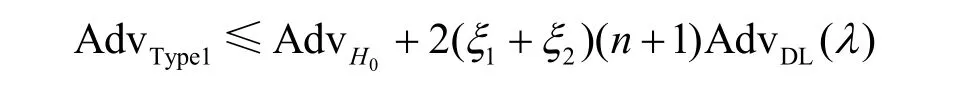
定理1证毕。

定理2假设第2型敌手最多ξ2次查询预言机KeyGen，ξ3次查询预言机Trapdoor，表示敌手A打破哈希函数H0的优势，AdvDL(λ)表示敌手A打破DL假设的优势，则第2型敌手打破密文不可区分性的优势为

定理2的证明过程与定理1相似，在此省略。

定理3如果敌手AI以ε的优势在数据块f[i]上产生时间跨度为t1的伪造，通过模拟GameI，并对哈希查询进行qH次查询、签名查询进行qS次查询和系统参数查询进行qparam次查询，则用以下的概率和多项式时间解决CDH问题

其中，tsm是G中的一个标量乘法的时间，e是自然对数的底数。

证明A为攻击者，A通过使用算法B模拟GameI与AI交互以解决CDH问题，这里哈希函数H被视为随机预言机，列表LH由B维护，该列表最初为空。

AI在GameI的各个阶段进行查询，而B在整个游戏中对AI的所有查询做出相应答复，B由A维护。

1)系统参数查询。首先AI请求B进行系统初始化，B回答此查询如下。B选择一个随机数t∈Zp作为密钥，生成公钥gt∈G，并将(g,gt,G)发送给AI，t保密。

2)哈希查询。AI可以在任何时间进行哈希查询，为了跟踪AI所查询过的每个数据块f[i]，B生成一个列表LH:{f[i],wi,ki,cl}，该列表最初是空的。要回答此查询B需执行以下操作。B检查列表LH对数据块f[i]之前是否查询过，如果找到，则B响应H(f[i])=wi作为答复；否则，B随机选择cl∈{0,1}使cl=0的概率为=δ。B选择一个随机数，并计算然后将元组添加到列表LH中，并响应作为AI回答。

3)签名查询。AI为数据块f[i]制作签名查询，B对此查询进行以下回答。B首先发出哈希查询以获得列表LH，然后检查cl，如果cl=0，则B报告失败并停止；否则，如果，并设置B对AI的伪造响应为σi，最终AI生成，假设AI为数据块f[k]生成一个伪造的签名，且没有为f[k]发出签名查询，现在B执行以下步骤生成一个伪造签名。

①B为f[k]发出哈希查询来获取列表LH，B检查cl的值，如果cl=1，B停止操作。

② 如果cl=0且h(f[k])=wi=gbϕ(g)k，则有

B知道的值，因此B可以计算gab或者可以在多项式时间内解决G中的CDH问题，这与CDH问题困难性的假设相矛盾。

B要成功需要3个事件。

E1：AI的任何签名查询都不会终止。

E2：AI为数据块f[k]生成真实且不重复的签名σk。

E3：AI会产生有效且不重要的伪造签名，B不终止是可能的。

推论1AI的任何签名查询都不会终止AI的概率至少为

证明如上所述，P[cl=1]=(1-δ)，因此B不会终止的概率为(1-δ)，因为它至少进行qS次签名查询，所以A查询后不会终止的概率至少为(1-δ)qS。

I

推论1证毕。

推论2AI签名查询后并为f[k]生成一个有效的签名且没有终止的概率为P(E2|E1)≥ε。

推论3在事件E1和E2发生并且B没有终止的情况下，AI产生有效且不重复伪造的概率为P(E3|(E1∩E2))≥δ。

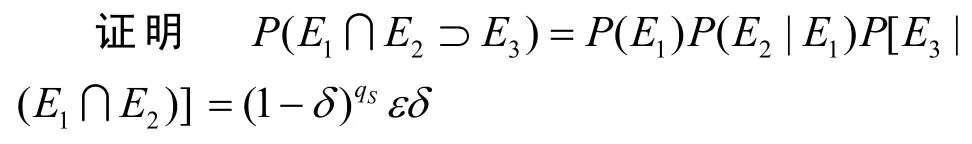
因此，有

为了找到ε'的最小值，对式(5)求偏微分

推论3证毕。

接下来，进一步证明B在多项式时间内解决CDH问题。

1)算法B的运行时间等于敌手AI的运行时间与对哈希查询(qH+qS)的响应时间以及签名查询(qS)的回应时间之和。

2)每个查询都需要计算群G中等于tsm的求幂运算。

根据1)和2)，算法B解决CDH问题的总时间为t1+tsm(qH+2qS)≤tc。

定理3证毕。

7 性能分析

7.1 计算量比较

在此，对文献[9,16,25]方案以及本文方案进行计算量比较。符号注释如表1所示。假设CSP能够诚实地执行操作，返回的结果为非空集合，本文对各个方案算法的计算量进行比较，如表2所示。

表1 符号注释

表2 计算量比较

通过表2可知，本文方案在搜索算法中的效率比文献[9]方案、文献[16]方案和文献[25]方案高。

7.2 功能比较

对文献[9]方案、文献[16]方案、文献[25]方案以及本文方案进行功能比较，如表3所示。

表3 功能比较

由表3可知，文献[9]方案和文献[16]方案不支持动态更新，虽然文献[25]方案和本文方案能够实现同样的功能，但是文献[25]方案是利用代理重加密技术更新数据拥有者以及部分密文实现方案的动态更新，大大增加了开销。而本文方案通过对Merkle-Tree的操作实现数据的动态更新（数据的添加和删除操作）。

7.3 仿真分析

在两台机器上进行了实验，其中一台CPU为Intel Core i5 3230M，内存为4 GB，操作系统为Windows10；另一台CPU为Intel Core i5 10210U，内存为8 GB。选用C++作为编程语言，分别来模拟运行Encrypt算法和Search算法。如图5所示，本文使用从0到1 000的不同数量的关键词运行了6个实验，比较了加密所有关键词和查找具有给定搜索令牌的匹配关键词密文的执行时间。结果显示，加密整个关键词与查找匹配的关键词密文相比，加密整个关键词的成本更高。但加密整个关键词只执行一次，而找到匹配的密文则需要对每个搜索请求执行一次。

由图6可知，在KeyGen算法中，文献[25]方案的计算成本几乎随着DO的数量线性增加，由于文献[25]方案利用代理重加密技术实现对数据拥有者和部分密文的更新，则对于不同的DO需要生成不同的密钥，因此增加了计算开销。而本文方案通过对Merkle-Tree的操作实现数据的动态更新，不需要对数据拥有者进行变更，所以本文方案在密钥生成算法中计算开销相对平稳，优于文献[25]方案。

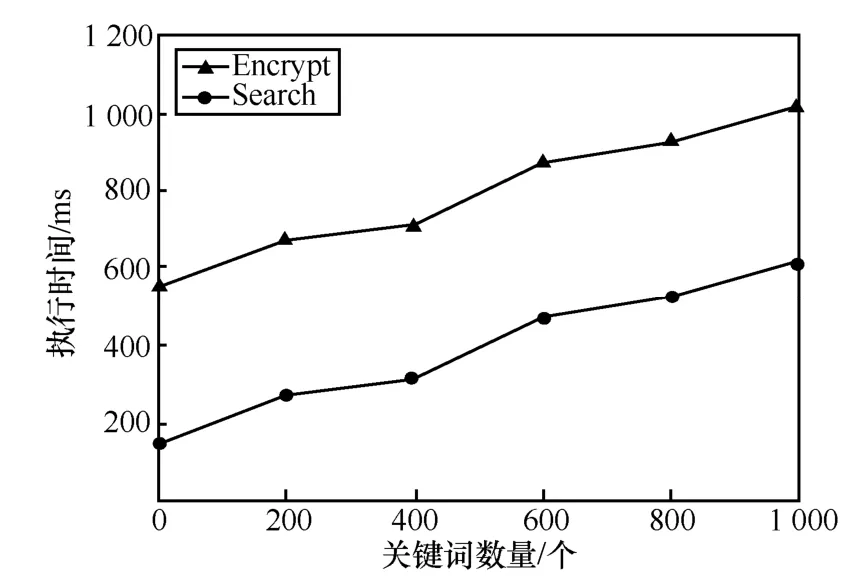
图5 执行时间

图6 密钥生成时间

为了实现一个高效的动态方案，本文利用改进的Merkle-Tree对文献[16]方案进行拓展实现动态更新。图7为更新数据块的数目在50到500变化的情况下进行文件更新的模拟实验。本文模拟了10个实验。从图7中可以看出，随着修改数据块数目的增加，计算成本逐渐增加，最后趋于平稳。故本文方案在计算成本上有一定的优势。

8 结束语

本文提出了搜索结果高效验证的多关键词搜索方案，实现了文献[16]方案不能实现的动态更新功能。首先，利用改进的Merkle-Tree认证方法构造搜索方案的验证及更新算法，不但防止了数据篡改、删除和伪造等不法操作的高效验证，而且时间戳字段与根节点的连接保证了数据的新鲜度；其次，对方案的正确性和安全性进行了详细的分析与证明，证明了本文方案满足密文不可区分性和不可伪造性；最后，性能分析表明，本文方案满足高效验证需求下具有低计算成本和更多安全功能的优势。

图7 修改数据块的计算成本