互操作性与自治性平衡的跨域访问控制策略映射

诸天逸，李凤华，金伟，郭云川，房梁，成林

（1.中国科学院信息工程研究所，北京 100093；2.中国科学院大学网络空间安全学院，北京 100049；3.中国信息安全测评中心，北京 100085）

1 引言

不同机构独立运维现状要求必须对信息系统与数据进行分域管理，这些信息系统呈现域内互联、域间孤立特征，使这些系统的数据不能被充分利用，这与系统互联的信息传播与共享协同本质相悖。为了消除当前信息系统域间孤立特征，需要将现有孤立系统进行物理/逻辑连接，提升数据共享能力。这种物理/逻辑连接打破原有信息系统在管理上数据隔离现状，带来了新的访问控制问题：如何确保跨域的数据访问者只有在受控模式下才能获得完成业务功能所需的数据。针对该问题，同时为了降低系统建设成本，需要设计恰当的访问控制策略跨域映射机制，将各系统已有的访问控制系统进行逻辑连接，为跨域用户分配完成任务所必需的最小权限，实现数据受控交换。例如，若域A用户需要访问域B的某些资源，可根据域A用户在本域已有的角色和域B中拟访问的资源，将域B内相应的角色分配给域A用户，使域A用户通过域B角色访问这些资源，通过这种方式实现成本约束的数据受控使用。

跨域访问控制策略映射机制包括2种：运行时策略映射机制[1-5]和配置时策略映射机制[6-11]。运行时策略映射机制是指用户跨域访问时与交互域在线协商授权策略，交互域结合当前自身角色层次的激活等情况，评估其请求操作中完成预期任务所需的最小权限或角色，并将之返回给跨域访问请求用户，以此保障域间互操作的动态授权。这种机制动态协商访问权限，应用场景广泛。但是由于交互域策略语法和语义方面差异巨大，域间的松散耦合性质不同，使多域策略无法集成融合，因此难以生成适用多个交互域的访问控制策略。此外该机制采用在线多次交互方式协商权限，授权效率低。针对该问题，研究者提出了目前使用较为广泛的配置时策略映射机制，该机制将各个自治域的访问控制策略和人为设定的权限或角色映射关系作为输入，并采用整数规划等方式以域内自治性等为代价消解这些映射可能导致的策略冲突，提升互操作性。该方式能生成全局适用且无冲突控制策略，适用于数据资源高频访问场景。但现有配置时策略映射机制存在如下问题。

1)未平衡互操作性和自治性损失。仅仅将自治域的自治性损失作为约束条件，以此获得最大化互操作性，不能动态平衡互操作性和自治性损失。

2)不能自动生成目标函数和约束函数。依赖大量人工操作，在庞杂的现实权限映射关系中，约束规则错综复杂，无法通过人工操作有效处理。

3)模型开销大、实际可行性低。现有方案以多种方式建模解决策略映射中冲突消解等典型问题，考虑的权限关系简单、典型，但是当角色、用户、权限等数量庞大关系复杂时，模型开销极大，可行性低。

为了解决上述问题，本文提出了域间访问控制策略映射与冲突检测消解方法，该方法基于具有约束的NSGA-III（non-dominated sorting genetic algorithm,the third version）算法来平衡域间互操作性和域内自治性损失，并消解跨域策略冲突。本文的主要贡献如下。

1)建立了最大化域间互操作、最小化域内自治性损失的整数规划方程，在传统域间访问控制约束的基础上加入前提条件与基数等约束，使模型更接近实际应用。

2)提出了带约束的NSGA-III进化算法，用二进制编码方式求解所建立的整数规划方程，加入惩罚函数降低不符合约束的个体的环境适应度。算法的时间复杂度为O(n2m)，其中，m为目标函数个数，n为种群大小。

3)在接近现实机构的数据集上测试了所提出的方案，实验数据表明，改进的算法在解决具有1 950维决策变量的问题时，仅用3 200代就使目标函数达到收敛，并且解的种类数目维持在300（种群大小为300），运行快速、收敛高效、非劣解多样。

2 相关工作

多域异构的访问控制策略、语义、表示、组织方式等让跨域授权问题成为研究难点，策略映射作为广泛应用的一种跨域访问控制机制已在许多场景实现安全互操作。

2.1 运行时策略映射机制

Joshi等[1]关注多域角色映射的冲突问题，将角色划分为激活、继承等多种约束层次关系，提出的GTRBAC（generalized temporal role based access control）约束模型是域间运行时策略映射的基础模型。但该模型局限于对层次关系的讨论，烦琐的角色关系不便于跨域互操作的实现。Du等[2]在此基础上，将角色层次关系简化为激活层次关系、继承层次关系和继承激活层次关系，讨论松散耦合环境中的运行时策略映射问题，解决多域环境中这3种混合层次结构的安全互操作问题。但整体策略维护困难，角色层次的管理问题突出，对松散耦合环境的普适性不高。Zhang等[3]针对新兴环境的松散耦合环境提出一种请求驱动的运行时策略映射安全互操作框架，实现在RBAC（role based access control）松散耦合环境中的安全互操作。但松散耦合环境下的域间信任问题还未解决。Shahraki等[4]认为依靠中央管理的授权不安全，提出分散、多权限的基于属性的访问控制模型DMA-ABAC（decentralized multi-authority attribute-based access control），其跨域运行时授权结合基于属性的访问控制和基于属性的组签名，能抵抗第三方攻击，但处理效率有限、无法同时处理大量访问请求。Unal等[5]结合移动网络的运行时环境，提出多域运行时策略映射模型FPM-RBAC（formal policy model for mobility with role based access control），能根据域间策略运行时指定和检查移动用户跨域互操作的安全性，但是该方案不能自动验证移动网络的安全策略，框架的集成规范需要完善。

运行时策略映射机制为跨域互操作提供灵活性、便捷性，适用于多种新兴的分布式环境，如移动网络、医疗服务等领域。但需要管理员的干预较多，策略的运行时维护也较复杂。

2.2 配置时策略映射机制

Kapadia等[6-7]提出的IRBAC2000（interoper-able role-based access control 2000）模型及A-IRBAC 2000（administrative IRBAC 2000）模型是跨域策略映射的开端，联合2个自治域，建立了一套全局配置时角色层次关系，但模型未解决因此产生的策略冲突。Shehab等[8]在IRBAC 2000基础上提出SEART（secure role mapping technique）模型，结合有向图并增加角色禁止访问关系，用路径签名算法实现分布式环境下配置时的多域全局映射的互操作，但该算法需用户枚举目标域角色路径，角色关系复杂时选择标准效率低。Shafiq等[9]将角色冲突分类，提出IP（integer programming）整数规划的方法进行冲突消解，将多域的策略两两映射合成，从而形成多域通用的配置时映射策略，但其仅考虑部分典型跨域冲突，角色映射关系极大丰富时，基于图形的规范模型实现困难，策略映射合并算法拥有指数复杂度。为解决社交网络中不同域内的用户跨域访问的安全性问题，Fan等[10]使用基于对称加密和CP-ABE（ciphertext policy attribute based encryption）混合加密算法，提出一种基于多权限属性加密的跨域访问控制方案，该方案尽管使用了代理用户以减少部分开销，但对规模庞大的社交网络用户来说，系统整体效率较低，对用户的分级授权不易实现。Diao等[11]指出目前策略映射的过程是一项劳动密集型任务，需要大量人工操作，因此提出一种智能角色映射推荐过程，可以根据角色的相似性自动生成2个域间的配置时策略映射，但提出的映射技术并没有得到验证，且未评估其可用性。

配置时策略映射机制让用户能在不同域间用统一方式进行访问控制授权，解决特定场景跨域互操作中的策略冲突，简化管理。但难以解决复杂环境下策略映射的人工工作量大、开销大、效率低的问题，无法应对域内策略的频繁变动。

现有策略映射机制的主要思路是在运行时或配置时将多个自治域的不同策略进行一致性协调，消解冲突并统一映射策略，使用时管理员根据访问控制要求变化对映射策略更新调整。但这些方法在规模庞大、“角色-用户-权限”关系复杂的现实环境下，可行性低，并且对冲突消解后自治域的自治性考虑较少。

本文提出的最优化互操作与自治性的跨域访问控制策略映射机制，综合考虑多个自治域间的互操作性和自治性损失间的平衡，用2种启发式算法在域间互操作性、自治域自治性损失度、策略多样性等指标上对优化效果评估。该机制能应对复杂的角色层次关系，并自动生成冲突约束、目标函数等，简化人工操作，提高了方法的适用性。

3 问题背景与描述

3.1 跨域访问控制策略映射

为提高域间互操作性，需将不同域的访问控制策略进行映射，图1给出了一个域间RBAC策略映射的示例，该示例包含2个域（域A和域B），其中，域A包含5个角色（即r1、r2、r3、r4和r5）和6个用户（即u1、u2、u3、u4、u5和u6）。域B包含4个角色（即r6、r7、r8和r9）和7个用户（即u7、u8、u9、u10、u11、u12和u13）。相关概念如图1所示。

1)域内用户/角色分配、角色层次和SoD冲突描述

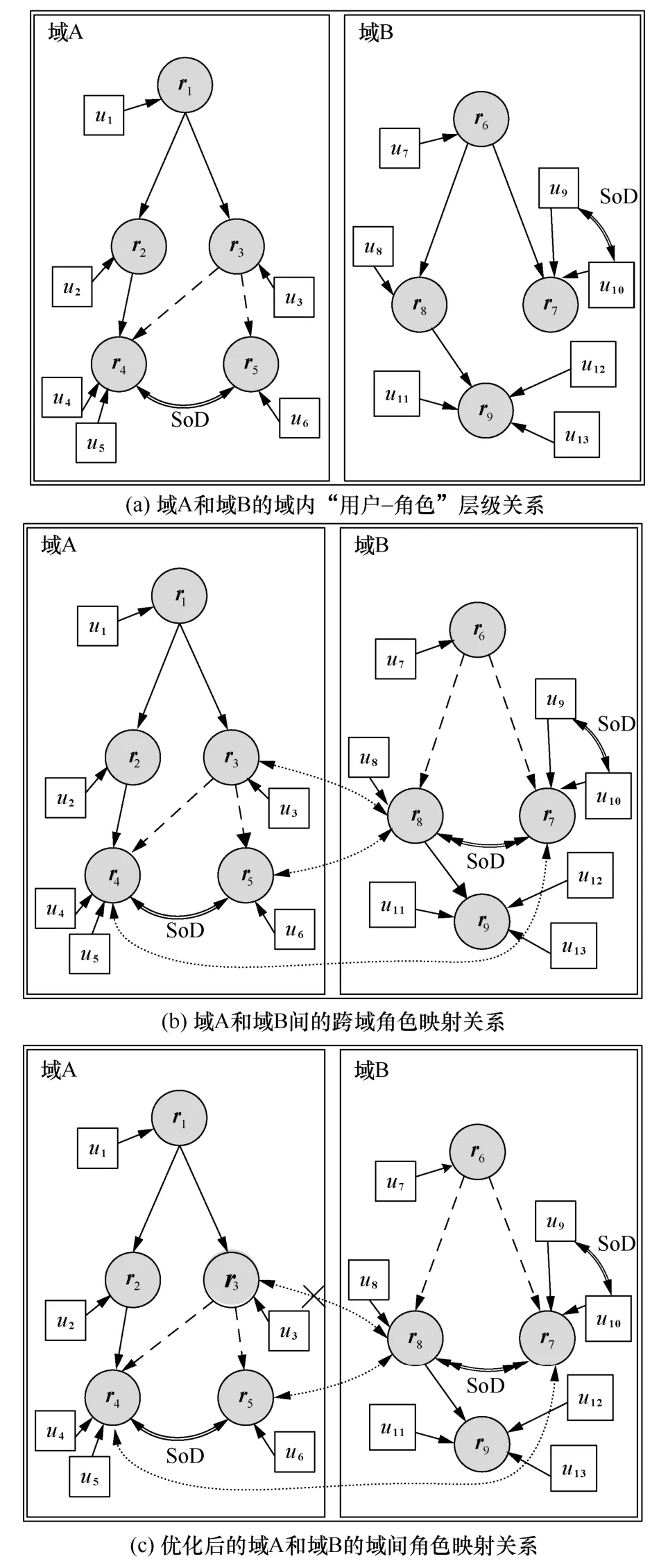
图1 域间RBAC策略映射的示例

如图1所示，用户和角色间的单向实线箭头表示为用户分配角色，如表示为用户u1分配角色r1。如果2个具有互斥权限的角色被分配给同一用户，这种违规称为角色间的职责分离（SoD,separation of duty）冲突。角色间SoD冲突用带SoD标记的双向双线箭头表示，如表示r4和r5间存在角色SoD冲突。如果某角色被同时分配给来自2个冲突用户集的用户，这种违规称为用户间SoD冲突。用户间SoD冲突用带SoD标记的双向单线箭头表示，如表示u9和u10间存在用户SoD冲突。此外，角色层次关系包含激活层次关系（即A-层次关系）和继承层次关系（即I-层次关系），其中，A-层次关系表示激活之后，被继承角色才能授予继承角色的权限；I-层次关系表示不需要激活，被继承角色就能授予继承角色的权限。在图1中分别用单向实线箭头和单向虚线箭头表示A-层次关系和I-层次关系；形式地，这2种关系分别记为≥A和≥I。r1≥Ir2表示，不需要激活，被继承角色r1直接授予继承角色r2相关权限；如r3≥Ar4表示，激活之后，被继承角色r3才能授予继承角色r4相关权限。

2)跨域角色映射与冲突消解

如图1(a)所示，原始的域A和域B之间不存在任何跨域互操作。需要进行跨域互操作时，管理员在域A和域B的部分角色间建立跨域映射连接，此时域A和域B形成一张全局的映射关系图，如图1(b)。

若2个本地角色间存在诱导角色SoD冲突，那么连接这2个角色的上级角色无法同时激活这2个角色，因此上级角色与下级角色间的继承关系将变为A-层次关系（激活层次关系），如r6≥Ir7将变为r6≥Ar7。这种改变导致自治域层次关系变化，降低域的自治性来提高跨域互操作性。

另一方面，添加跨域映射连接后，2个域之间可能存在跨域冲突，为保障域的自治性，确保跨域映射的安全性，需对本地域的策略调整删减。如图1(c)所示，由于在r8和r3之间、r8和r5之间均存在跨域映射连接，但这种连接会导致u6通过r8间接获取r3的权限，造成关联冲突，一种可行的方式是删除r8和r3间的跨域映射连接。

3.2 问题形式描述

虽然跨域角色映射可增加域间互操作性，但也导致域内的自治性损失。为平衡跨域访问控制的域间互操作性和域内自治性，本文将该平衡问题建模为多目标整数规划优化问题，其中目标函数包括最大化域间互操作性函数和最小化域内自治性函数，如式(1)所示。

如3.1节中的图1(c)所示，SAB表示为域A的所有用户分配的域B中的角色集合，即表示可以为域A中的用户u1分配域B中的角色r8，表示可以为域B中的用户u7分配域A中的角色r5。wA和wB分别表示域A和域B中“用户-角色”分配的权重，权重越大在优化过程中该域策略被保留的可能性更高。例如，若域A的权重较大，则结果中域A用户对域B角色的授权访问将更高概率保留，相反，域B用户对域A角色的授权访问将更低概率保留。同理，表示为域A中用户u1分配本地域角色r1，表示为域B中用户u7分配本地域角色r6。NA和NB分别是域A和域B在跨域映射连接之前自治域内部分配的“用户-角色”的数量，在图1(b)中，NA=13，NB=11。跨域映射连接之后，部分域内“用户-角色”因跨域冲突无法继续授权将导致自治性损失，如由此计算域内自治性损失的比例。

从上述讨论可以看出，规划方程将以下两部分作为多域映射策略的输入：1)域A和域B的域内角色分配关系、层次关系和冲突关系；2)管理员定义域间的部分角色映射关系。输出符合约束函数、全局无冲突的跨域访问控制策略。以图1(b)为例，若域A权重为2，域B权重为3，则3个目标函数分别表示为

4 基于NSGA-III的策略映射算法

现实应用场景下的域内用户和角色数量较多，导致难以准确快速求解式(1)～式(4)所定义的多目标整数规划优化问题。针对该问题，本文基于NSGA-III的策略映射算法有较低的复杂度（O(n2m)），能准确快速、较全面地搜索解集。

4.1 相关定义

本文使用的函数与谓词具体释义如表1所示。

定义1角色集。域D内所有角色的集合用表示，其中，n为域D内角色数量。

定义2用户集。域D内有角色，其用户集为拥有角色ri的用户所构成的集合，其中，k为拥有角色ri的用户数。

定义3角色SoD约束。给定域D内有角色表示与ri存在角色SoD约束关系的角色集合，定义如式(5)所示。

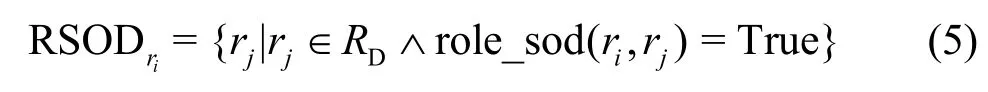
其中，role_sod(ri,rj)=True 表示ri和rj存在角色SoD约束，即对于同一个用户，不能同时被授予角色ri和rj。

表1 函数与谓词具体释义

定义4用户SoD约束。给定域D内有角色ri用户集内的2个用户和间存在用户SoD约束，则互相冲突的2个用户之间构成冲突用户的二元组，表示为(um,un)。用USODri表示ri的用户SoD冲突对象集，其定义如式(6)所示。

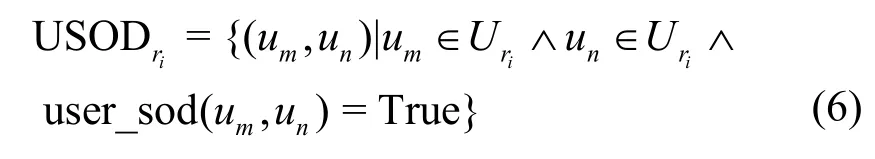
其中，user_sod(um,un)=True 表示um和un间存在用户SoD约束，即对于同一个角色，不能授权给2个冲突的用户um和un。

定义5角色映射连接。给定域D1内有角色ri(ri∈RD1)，域D2内角色rj(rj∈RD2)存在映射关系，用Mri表示所有与角色ri有映射关系的角色rj组成的集合，如式(7)所示。

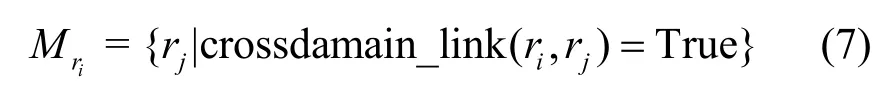
为了简化问题，避免约束过度复杂，本文中考虑的每个角色的跨域映射连接数量少于3个，即。

定义6角色层次关系。给定域D内有角色其所有上下级关联关系（包含I-层次关系及A-层次关系）用四元组表示，其中，isn为I-层次的直接上级节点集，ijn为I-层次的直接下级节点集，asn为A-层次的直接上级节点集，ajn为A-层次的直接下级节点集。

若ri具有本地域内上级I-层次关系的节点，则返回本地域内其上级I-层次关系的节点集，如式(8)所示。

若ri具有本地域内上级I-层次关系的节点，则返回本地域内其下级I-层次关系的节点集，如式(9)所示。

若ri具有本地域内上级I-层次关系的节点，则返回本地域内其上级A-层次关系的节点集，如式(10)所示。

若ri具有本地域内上级I-层次关系的节点，则返回本地域内其下级A-层次关系的节点集，如式(11)所示。

定义7角色标签。给定域D内有角色其标签用八元组来表示，如式(12)所示。

4.2 目标函数生成

4.2.1域间互操作性

域间互操作是指自治域的用户通过跨域角色映射后实现数据交互访问。即本地角色被授予交互域角色的授权，并获得其权限，域间的跨域交互越多，说明域间互操作性越强。

定义8给定用户集合为(i≤j)，角色集合定义SUR为U内所有用户被赋予的角色数之和，即

域间互操作性目标函数根据域间已经确定的角色映射连接生成。目标函数生成算法如算法1所示，具体如下。

1)搜索域A中的所有角色节点，记录与域B有直接映射连接关系的角色，记集合为

域A用户通过跨域角色映射连接对域B角色的访问表示为

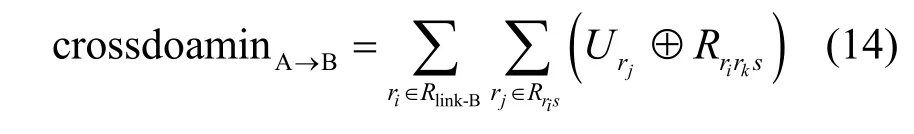
同理，得出域B用户通过跨域角色映射连接对域A角色的访问表示为crossdoaminB→A

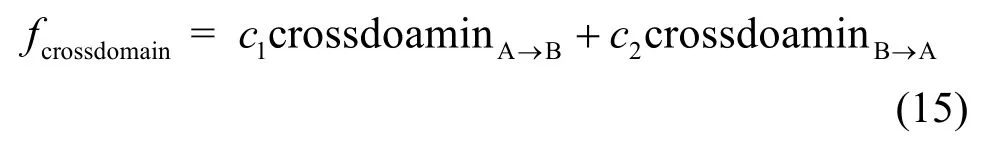
例1对于图1(b)实例，取域A的权重为2，域B的权重为3（c1=3,c2=2），即

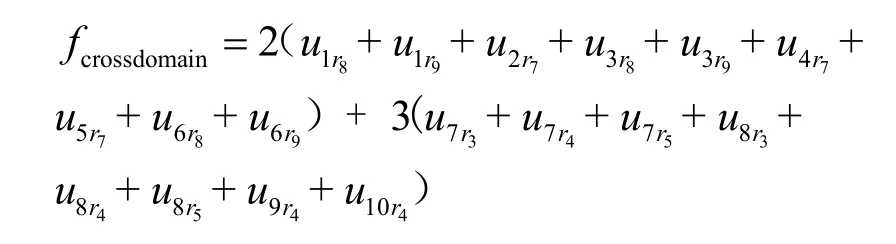
由于求解的最大化域间互操作性为最大值求解，为NSGA-III算法计算方便，将其转换为求解上式的最小值。

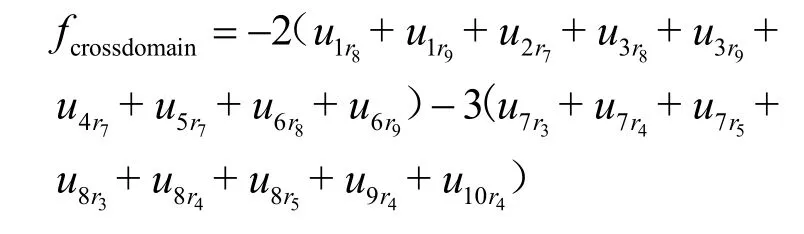
4.2.2域内自治性损失

域内自治性损失，是指消解角色SoD冲突、用户SoD冲突、关联冲突等所导致的本地“用户-角色”授权分配的损失度。

自治性损失目标函数主要根据域间互操作前后，域内的访问控制授权数量生成。目标函数通过如下过程生成：遍历域A在没有跨域访问控制连接时，所有可能的本地域访问控制映射。对于域A任意的ri(ri∈RA)，其中RA为域A的全部角色集合，ri的授权用户集表示为。具体如算法2所示。

例2对于图1(b)实例，域A和域B的域自治性损失的目标函数为

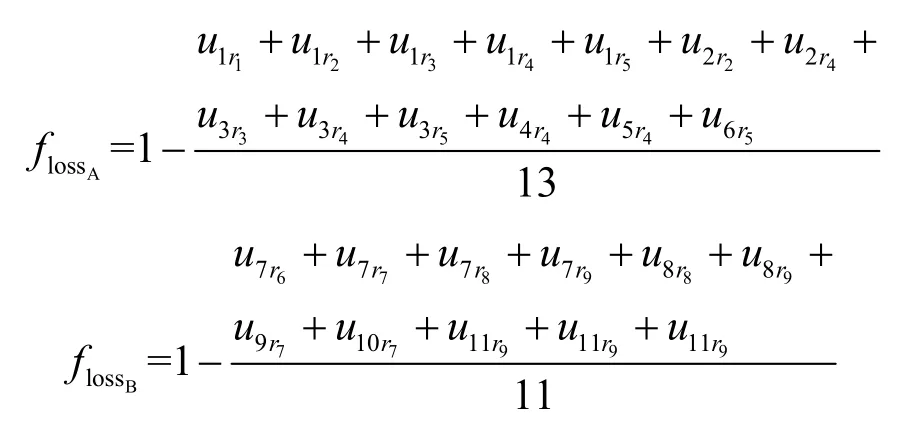
4.3 访问控制约束

本文考虑以下7种（固有关系约束、角色SoD约束、用户SoD约束、前提条件约束、基数约束、诱导SoD约束、关联冲突约束）典型跨域访问控制冲突，将其转换为约束方程，利用IP整数规划方法求解全局无冲突的跨域访问控制映射策略，约束方程的生成算法将在4.4节具体说明。本文用Uk表示域k的用户集，Rk表示域k的角色集，7种约束描述如下。

1)固有关系约束。在未经优化的跨域访问控制策略中，本地域的一些“用户-角色”授权关系（如用户通过I-层次关系访问本地角色）不会因跨域互操作而改变，这些关系将保留在优化后的全局策略中。

2)角色SoD约束。当2个角色所对应的权限互相冲突时，这2个互斥角色不能同时被授权给同一个用户。

3)用户SoD约束。出于系统安全性考虑，一个角色的2个互斥用户不能同时被授权访问该角色。

4)前提条件约束。只有当不同域的2个角色之间的跨域角色映射连接存在时，本域的高级角色才能连接外域角色。

5)基数约束。出于系统安全性考虑，一个角色被分配的用户数量受限。

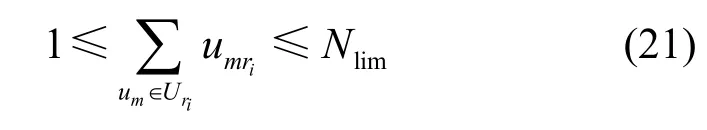
6)诱导SoD约束。若本域的2个角色间存在角色SoD约束，那么这2个角色通过跨域角色映射连接所对应的外域的2个角色间也存在角色SoD约束，称为诱导SoD约束。

若域k内的2个不同角色间存在角色SoD，而域l内的2个不同角色间也存在角色SoD，则对于任意域内或域外用户um，表示为

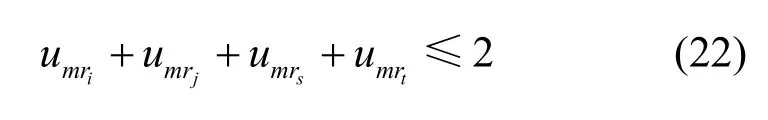
7)关联冲突约束。本域用户通过跨域角色映射连接访问外域角色，并再次通过其他跨域映射角色连接访问本域高级角色，使本域用户非法访问本域的高级角色，从而造成跨域冲突。

若rj是um的授权角色，ri是un的授权角色，存在如下关系

ri与rj间存在跨域角色连接，记为间存在跨域角色连接，记为表示为

4.4 约束条件生成

在跨域分布式协作场景中，角色、用户和权限之间的约束关系广泛存在，为确保跨域策略的无冲突融合、本地策略的安全变动，要完整地生成约束函数。但利用管理员或人工分配的方式效率低、成本高，且难以维护[2,12]。针对上述问题，本文提出约束函数的自动生成算法，对不同的约束条件生成对应的等式或不等式约束。生成算法包括固有关系约束生成算法、角色SoD约束生成算法、用户SoD约束生成算法、前提条件约束生成算法、基数约束生成算法、诱导SoD生成算法、关联冲突约束生成算法。具体如下。

4.4.1固有关系约束生成算法

固有关系约束生成算法的核心思想如下：首先遍历RD中每个角色ri，剔除ri中那些授权用户中存在用户SoD约束的角色（因为那些“角色-用户”的授权关系不能直接确定）；求解ri的I-层次下级角色得到集合Ri，因跨域策略优化可能导致ri的授权用户无法被分配到A-层次的下级角色，因此只考虑I-层次下级角色；最后遍历用户集内的角色um，根据4.3节的固有关系约束生成约束等式，并加入约束集合。具体算法如算法3所示。

4.4.2角色SoD约束生成算法

给定域k与域l进行跨域互操作，且2个域内所有用户的集合为Ukl，角色SoD约束生成算法的输入为域k与域l内所有角色，记为Rk，输出为一个存放角色SoD不等式约束的集合，记为C2s。

角色SoD约束生成算法的核心思想如下：首先遍历Rk中每个角色ri，判断其RSODri标签是否为空，若为空则判断下一个ri，否则继续执行；其次遍历RSODri内每个角色rj，并遍历所有用户集合Ukl中的每一个用户um，根据角色SoD约束生成约束不等式，并加入约束集合。具体算法如算法4所示。

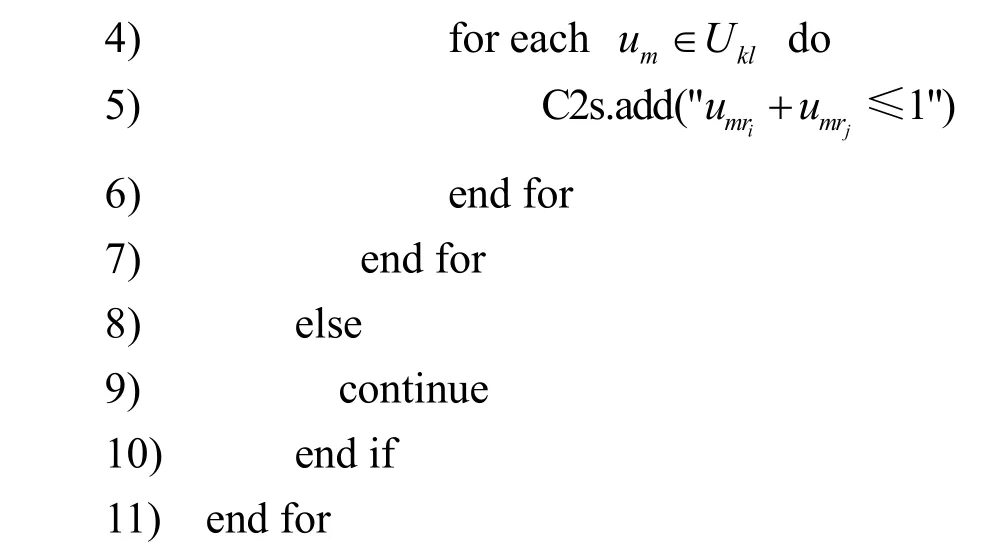
4.4.3用户SoD约束生成算法

给定域D内有角色ri，其授权用户集为Uri，用表示中的冲突用户二元组，其中，是2个冲突的用户。用户SoD约束生成算法的输入为域D内所有角色，记为RD，输出为一个存放用户SoD的不等式约束的集合，记为C3s。

用户SoD约束生成算法的核心思想如下。首先遍历Rk中每个角色ri，判断其标签是否为空，若为空则判断下一个ri，否则将其加入RSoD。其次遍历RSoD中每个角色rj，对每个rj首先查找其所有A-层次或I-层次的本地域下级角色，记为接着查找其所有A-层次或I-层次的交互域下级角色，记为分为两步生成：1)在中搜索每个角色rl是否拥有跨域连接；2)对于拥有跨域连接角色，获取rl的标签中每个角色的所有下级角色，添加到集合生成集合中每个角色rs；对于每个rs，中每个角色rt，结合中的用户对，根据用户SoD约束生成约束集合。具体算法如算法5所示。

4.4.4前提条件约束生成算法

给定域D内有角色ri和角色rj，2个角色的授权用户集分别为，外域K内有角色rl。前提条件约束生成算法的输入为域D和外域K内所有角色，记为RD和RK，输出为一个存放前提条件约束的不等式约束的集合，记为C4s。

前提条件约束生成算法的核心思想如下：首先遍历RD中每个角色ri，判断其标签是否为空，若为空则判断下一个ri，否则将其加入RM；然后遍历RM中每个角色ri，查找其所有上级角色放入集合；依次检索的中的角色rj，并判断rj与ri之间是否存在A-层次关系，根据前提条件约束生成约束集合。具体算法如算法6所示。

4.4.5基数约束生成算法

给定域D内有角色ri，其授权用户集为Uri，且同时激活的授权用户数量为Nlim。基数约束生成算法的输入为域D内所有角色，记为RD，输出为一个存放基数约束的不等式约束的集合，记为C5s。

基数约束生成算法的核心思想如下：首先遍历Rk中每个角色ri，判断其标签是否为空，若为空则判断下一个ri，否则继续执行；其次对标签不为空的ri，遍历其中每个用户um，并对求和；对以上求得的和根据基数约束生成约束不等式，并加入C5s。具体算法如算法7所示。

4.4.6诱导SoD约束生成算法

若域k与域l进行跨域互操作，um是任意域内或域外用户。诱导SoD约束生成算法的输入为域k与域l内所有角色，记为RD，输出为一个存放诱导SoD约束的不等式约束的集合，记为C6s。

诱导SoD约束生成算法的核心思想如下：首先遍历Rk中每个角色ri，判断其标签是否为空，若为空则判断下一个ri，否则继续执行；其次遍历ri的标签内每个角色rj；遍历ri的标签内每个角色rs；遍历rj的标签内每个角色rt；根据诱导SoD约束生成约束不等式，并加入C6s。具体算法如算法8所示。

4.4.7关联冲突约束生成算法

若域k内有un、ri、rl，域l内有um、rj。关联冲突约束生成算法的输入为域k与域l内所有角色，记为RD，输出为一个存放关联冲突约束的不等式约束的集合，记为C7s。

关联冲突约束生成算法的核心思想如下：首先遍历Rk中每个角色ri，判断其标签内跨域连接角色的个数是否大于1，若满足条件则用rj和rl分别表示其中的低级角色和高级角色，否则继续执行；遍历rj的标签中每个用户rn；对每个rn，遍历ri的标签中每个用户rm，根据关联冲突约束生成约束不等式，并加入约束集合。具体算法如算法9所示。

4.5 NSGA-III多目标优化算法

NSGA-III采用基于参考点的非支配排序算法，解决2～15个目标的多目标优化问题时速度快，且同时保证准确性和多样性，独特的理想点与小生境可避免在优化过程中陷入局部收敛，该算法的计算复杂性显著低于NSGA-II算法。相较于一般的遗传算法，NSGA-III算法需要设置的参数较少、使用方便，初始种群设置无依赖性，染色体使用二进制编码，找到最优解集后对问题解码方便。因此，本文采用带约束的NSGA-III多目标优化算法，在算法中将域间互操作性、域A的自治性损失和域B的自治性损失作为优化的目标函数，将生成的跨域策略冲突的约束函数作为算法的约束，其时间复杂度为O(n2logm-2n)或O(n2m)，其中n、m分别为种群个体数目、目标函数个数。算法主要包含以下9个部分。

1)染色体生成。在4.2.1节中，根据例1中图1(b)的实例得到fcrossdomain，如下式所示。

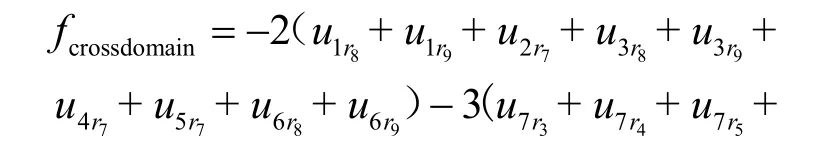
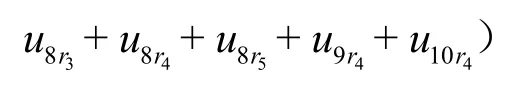
进行上述操作后，遗传算法种群中任意个体i可以表示为m+n+l维的决策变量，如式(24)所示。其中

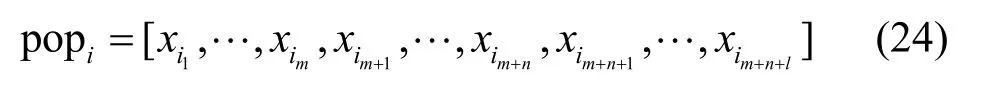
由每一代更新产生的所有染色体的集合，称为种群，用P表示。

2)约束条件生成。约束条件即4.3节提出的跨域访问控制约束，利用4.4节提出的约束条件生成算法生成。不符合约束条件的个体会受到不同程度的惩罚，从而淘汰那些不符合条件的个体，使解集中的解都满足约束条件。

3)种群初始化。在设置一系列算法参数的同时，需要对种群进行初始化操作。为了改进程序性能，使算法以最少的迭代次数达到收敛状态，需要生成一个适应度较好的种群。本文在初始化过程中，生成每个个体popi的同时，检查该个体是否满足所有的约束集合C内的条件，若满足则将该个体纳入种群，否则丢弃。生成初始种群P后，计算其适应度值。

4)参考平面生成。参考平面是一个归一化的平面，它与所有物镜轴都有一个截距，NSGA-III中的参考平面用Das等[14]的系统方法生成。该平面辅助寻找广泛分布在帕累托最优前沿或附近的解，以确保解的多样性。

5)交叉变异。将种群P复制为P'，对P'分别进行交叉和变异操作，使之可能产生更优的个体（即一种可能更优的跨域策略）。

6)适应度值计算。适应度用于衡量每个染色体所对应的一种策略的优良，即所对应的跨域互操作性、域A自治性损失度和域B自治性损失度的高低。如果染色体所对应的跨域互操作性越高、域A自治性损失度和域B自治性损失度越小，表示该染色体适应度越好。适应度值为一个三维向量，种群P中第i个个体的适应度值可以表示为。高适应度值的个体（策略组合）意味在迭代过程中以更高概率保留，低适应度值的个体（策略组合）意味在迭代过程中以更低概率保留，在本文中适应度值范围为[0,1]。与传统的NSGA-III不同的是，在计算P'的适应度值时，引入惩罚函数对不满足约束的个体进行对应维度的惩罚。首先根据3个目标函数和计算种群P'的适应度值，再判断P'中每个个体popi是否满足所有的约束等式和不等式条件C。若popi满足条件，则不修改其适应度值，否则，根据式(24)确定该个体涉及的不满足约束的二进制决策变量位置，并将此位置对应的适应度值置零。例如，当中含有不符合约束决策变量的决策变量时，则将均置为0（0为最低的适应度），以此降低该个体在迭代中保留下来的概率。符号表述如算法10所示。

7)理想点计算。理想点的三维度（3个目标函数）数值全部是种群中所有个体的最优值。NSGA-III中的理想点的作用与NSGA-II中拥挤度较为相似，都用于非支配排序，但在多目标优化表现更优。选取每一代种群中，在3个维度（跨域互操作性、域A自治性损失度和域B自治性损失度）最优的值作为理想点，越靠近理想点则该染色体被保留的可能性越大。将初始种群P中的N个个体和种群P'中的N个个体混合得到混合种群Pmix，其个体数量为2N，并计算其理想点坐标。即

8)下一代子代的选择。子代利用非支配排序和个体到理想点的距离，对Pmix中的2N个个体进行分层，选择其中的N个个体作为子代Pc。

9)计算产生的新种群Pc的适应度值，并判断当前的迭代次数，若迭代次数达到最大次数，则结束迭代，并进行画图及数值输出；否则，转向步骤5)。

带约束的NSGA-III算法的如算法11所示。

5 实验及分析

由于约束生成算法仅在程序初始化过程中运行一次，其运行时间和输入的角色节点、用户规模有关，本文测试的3种规模下，运行时间可以忽略不计。实验将穷举法、MOEA/D[13-14]这2种算法与本文提出的带约束的NSGA-III算法进行对照实验，多维度比较算法优劣。

5.1 实验设置

5.1.1实验环境

本文仿真实验用Python编程实现。开发工具为pycharm2018.2，开发环境为Windows 7 Enterprise（64 bit），Inter(R) Core(TM)i7-3587U CPU @ 2.1 GHz，10 GB内存。

5.1.2实验用例

为验证本文所提算法在实际问题中的适用性及效果。本文采用人为构造的数据集，该数据集根据现实的组织机构Z内的角色层级关系，并加入7类典型访问控制约束进行仿真。数据集分为小、中、大3种不同规模的域间角色关系数据集，将其作为输入测试算法性能。3种规模数据量如表2所示。

表2 不同数据集的域内和域间结构

5.2 结果分析

实验评价指标主要为3个，分别是种群中每个个体平均的互操作性（Avgcrossdomain）、域A自治性损失（AvglossA）和域B自治性损失（AvglossB），如式(26)～式(28)所示。

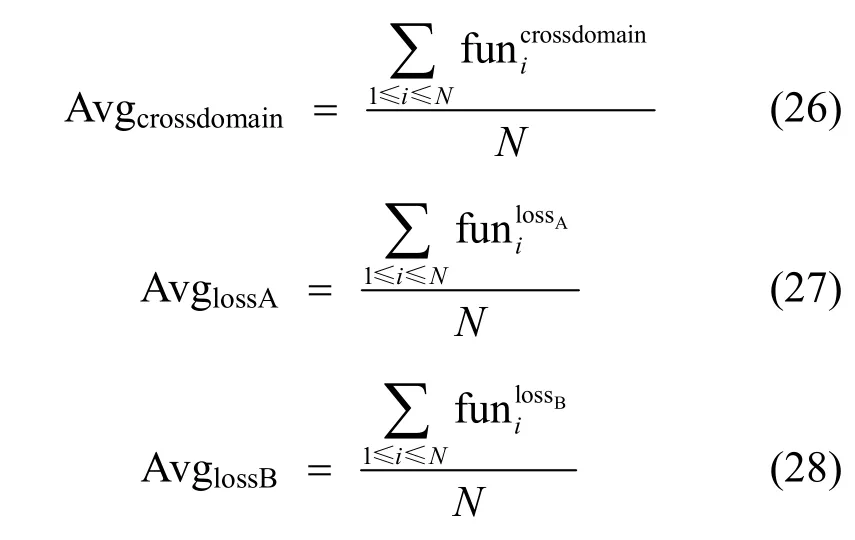
通过计算每一代种群中3个目标函数适应度值的均值，反映种群总体在3个维度的适应度变化。若随着迭代次数的增加，这3个指标变化较小或不再变化，即NSGA-III算法的解已经收敛。如4.5节中带约束的NSGA-III算法所示，如果连续5次满足第i+1代和第i代种群的3个指标（Avgcrossdomain、AvglossA和AvglossB）的数值分别相差不超过1‰，则认为3个评价指标达到稳定点。

本文在3种不同规模大小的数据集上进行测试，并在每种数据集上，分别用穷举法、MOEA/D算法与本文的带约束的NSGA-III算法进行对比。实验结果从多个维度进行比较：3个目标函数的评价函数（Avgcrossdomain、AvglossA和AvglossB）达到稳定点的时间，解的多样性、稳定性、准确性。

5.2.1小规模数据集测试

本文以小规模数据集（如图2所示）为例，详述优化操作的具体过程，根据4.2节目标函数生成算法生成3个目标函数，具体如下。

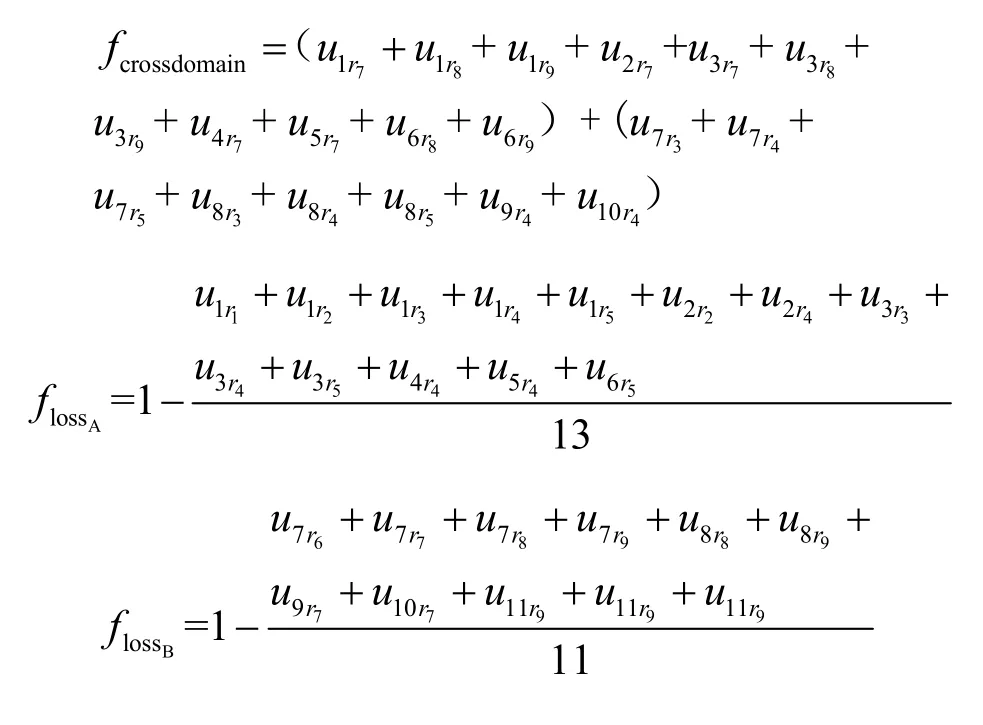
图2 域间RBAC策略映射的示例

根据4.4节约束条件生成算法，得到的约束等式/不等式如下所示。

小规模数据集测试设置的参数为：迭代次数50次，种群大小200，决策向量的每一位的交叉、变异概率为，测试中决策变量维度为43。

小规模数据集测试的输入图即为第3.1节的图1(c)，共生成约束24条，执行时间为4 s。

互操作性与自治性损失的稳定点。图3和图4分别是MOEA/D算法和带约束的NSGA-III算法的Avgcrossdomain、AvglossA和AvglossB这3条评价函数的变化曲线。MOEA/D算法的3条评价函数收敛曲线收敛速度较快，在7次迭代就趋于收敛，达到稳定点。带约束的NSGA-III算法的评价函数在16次迭代趋于收敛，相对于MOEA/D算法收敛速度较慢。穷举法实验中运行时间过长，即使是规模较小的数据集，也无法在有限时间内求解所有符合约束条件的正确解。

图3 MOEA/D的Avgcrossdomain、AvglossA和AvglossB指标变化曲线（小规模数据集）

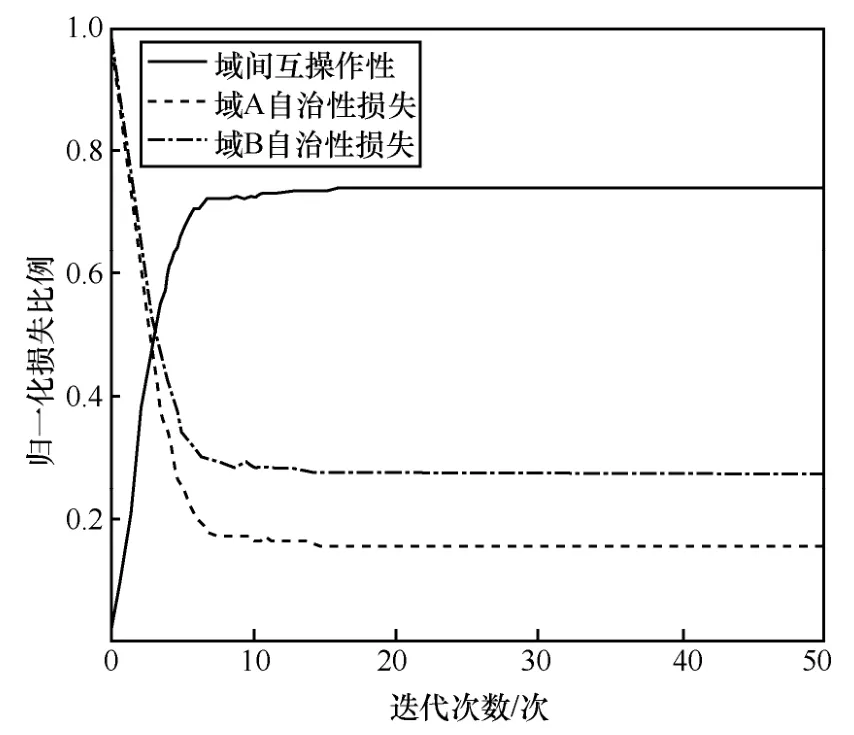
图4 NSGA-III的Avgcrossdomain、AvglossA和AvglossB指标变化曲线（小规模数据集）

图5和图6分别是MOEA/D算法和带约束的NSGA-III算法的解多样性变化曲线，可见带约束的NSGA-III算法的解具有丰富的多样性，多次试验的解集一致，且经验证这些解都是符合所有约束条件的正确解。MOEA/D算法的解多样性较差，算法容易局部收敛而无法得到所有全部正确的解，多次实验得到的解并不相同，且解集中含有少量的解并不能满足所有约束条件，即为错误解。

5.2.2中规模数据集测试

中规模数据集测试设置的参数为：迭代次数1 800次，种群大小200，决策向量的每一位的交叉、变异概率为。由于种群越大，每一代执行时间越长，测试中决策变量维度为2 556。中规模数据集测试的域A和域B的域内“用户-角色”层级分别如图7和图8所示，共生成约束276条，执行时间为4.5 h。

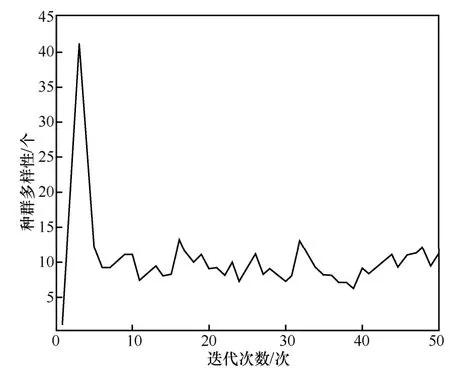
图5 MOEA/D的解多样性变化曲线（小规模数据集）

互操作性与自治性损失的稳定点。图9和图10分别是MOEA/D算法和带约束的NSGA-III算法的Avgcrossdomain、AvglossA和AvglossB这3条评价函数的变化曲线。MOEA/D算法在510次迭代后收敛并达到稳定点，带约束的NSGA-III算法在1 250次迭代后收敛并达到稳定点。

解的多样性、稳定性、准确性分析。图11和图12分别是MOEA/D算法和带约束的NSGA-III算法的解多样性变化曲线。由图11和图12可知，因MOEA/D算法容易陷入局部收敛，规模越大局部收敛越明显，即解的多样性越差。带约束的NSGA-III算法的解的多样性好，且更稳定。

5.2.3大规模数据集测试

大规模数据集测试设置的参数为：迭代次数5 000次，种群大小300，决策向量的每一位的交叉、变异概率为，测试中决策变量维度为6 539。

3个评价指标的变化趋势如图13所示，执行时间为91 h。大规模数据集测试中共有约束435条，因规模较大无法清楚显示细节，故不再给出“用户-角色”层级图。

从图13可以看出，算法在3 100代左右达到收敛，3个评价指标变化开始变小或稳定不变。

由带约束的NSGA-III算法解得的结果，去重后以文本形式输出，在大数据集测试下共得到200组符合约束的帕累托最优解，经验证这些解均为符合约束条件的可行解。

图6 NSGA-III算法的解多样性变化曲线（小规模数据集）

图9 MOEA/D的Avgcrossdomain、AvglossA和AvglossB 指标变化曲线（中规模数据集）

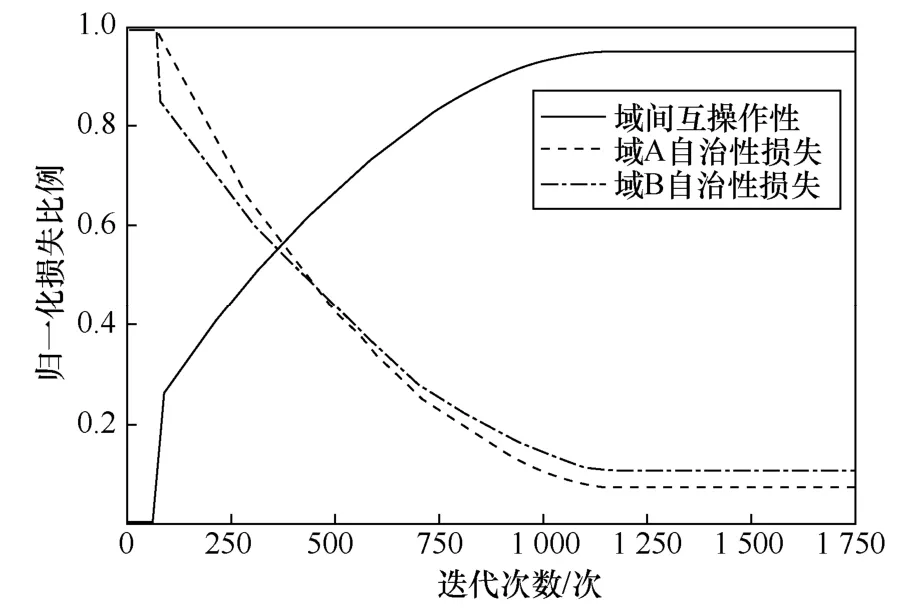
图10 NSGA-III的Avgcrossdomain、AvglossA和AvglossB 指标变化曲线（中规模数据集）

图11 MOEA/D的解多样性变化曲线（中规模数据集）

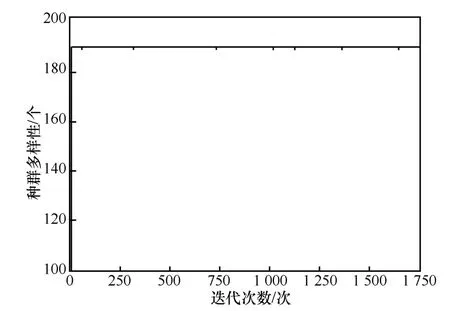
图12 NSGA-III的解多样性变化曲线（中规模数据集）

图13 NSGA-III的Avgcrossdomain、AvglossA和AvglossB指标变化曲线（大规模数据集）

Avgcrossdomain、AvglossA和AvglossB达到稳定点的时间、解的多样性、稳定性、准确性实验结果与中数据集测试相似。在多样性方面，由于解空间巨大，预设的种群大小为300，迭代过程中基本每一代保持了300种不同的染色体，直至达到稳定点后输出300种不同类型的染色体（即可行解）。

对3种规模实验下，穷举法、MOEA/D算法和带约束的NSGA-III算法进行比较。经过上述实验，可以得到下面的结论。

穷举法虽然准确性高，但运行时间非常长。无法处理复杂的域间映射关系，在应对多样的约束条件时，不能在有效的时间内解得可行解。在过去的多类相关研究中[8-9,11]，研究者着眼于模型、语义、模式格式和约束的研究，绝大多数采用管理员人工授权等，很少对其理论在实际场景中的可行性进行验证。穷举法对应管理员授权方式，在本文无实际输出结果，但也论证了在现实多约束环境下管理员方式的局限性。

带约束的NSGA-III算法同MOEA/D算法相比，虽然运行速度没有MOEA/D算法快，但其运行速度在现实中是可以接受的。并且带约束的NSGA-III算法在解的准确性和多样性方面，远优于MOEA/D算法。

6 结束语

本文针对如何平衡域间互操作性和域内自治性这一重要问题，提出一种基于多目标整数规划优化的跨域访问控制策略映射机制。首先，该机制可以平衡域间互操作性和域内自治性，保证域间互操作性最大化且域内自治性损失最小。在此基础上，该机制在传统域间访问控制约束的基础上加入前提条件与基数等约束，使模型更接近实际应用。在加入目标函数、约束函数自动生成算法后，大大减少了人工管理员的烦琐操作。最后，本文实现的带约束的NSGA-III优化算法，在模拟现实机构特征的小中大规模数据集上进行测试，实验结果进一步说明了机制的高效性和准确性。