类矩形盾构隧道结构极限承载力分析

2020-10-11赵子蓬叶宇航

同济大学学报（自然科学版） 2020年9期

柳献，赵子蓬，叶宇航，2，刘震

（1. 同济大学土木工程学院，上海200092；2. 广州地铁设计研究院股份有限公司，广东广州510000）

随着城市地下空间的不断开发，可利用的地下空间资源越来越少。因此，探索空间利用率高、施工环境影响小的地下空间开发手段是必然趋势。类矩形盾构隧道工法具有空间利用率高、施工扰动小等优势，是目前国内研究的热点，已成功应用于宁波市轨道交通3号线一期出入段［1］。目前，国内学者对类矩形盾构隧道工法研究尚浅，衬砌结构的受力性能与破坏机理不清晰，影响承载能力的关键因素尚不明确。为探究结构的破坏过程及最终破坏模式，明确影响受力性能及极限承载力的关键因素，需对类矩形盾构隧道受力全过程中的力学性能进行分析。

国内外学者通过整环足尺试验对带中柱的类矩形盾构隧道结构的受力性能、破坏机理、极限承载力［2］、整体安全性［3］以及结构受力性能受螺栓位置优化的影响［4］等开展了相应的研究，得到了特定型式下带中柱类矩形盾构隧道结构的破坏链、破坏机制与结构极限承载力，并引入鲁棒性指标对衬砌结构的整体安全性进行了综合评价［3］。此外，有学者采用立式足尺试验探讨了自重对无中柱类矩形盾构隧道结构受力性能的影响［5］，并对不同埋深下的结构受力性能、单环有效刚度、纵向接缝转动刚度、裂缝发展形式等开展了研究［6-7］。上述研究结果均基于足尺试验展开，具有一定的局限性。一方面，整环足尺试验存在一定的试验误差，如试验荷载采用分级加载方式可能导致结构受力性能点跳跃；另一方面，衬砌结构足尺试验体量较大且费用高昂，故只能针对某一型式下的结构进行研究，而无法进行参数化分析，无法具体说明各因素对结构极限承载力产生的影响。针对上述问题，需结合数值模型对衬砌结构的受力全过程进行模拟，分析类矩形盾构隧道衬砌结构的力学性能。

部分学者基于适用于圆形盾构隧道的修正惯用法、梁‒弹簧法及壳‒弹簧法等设计方法［8-11］，建立类矩形盾构隧道结构线弹性分析模型，得到适用于实际工程的有效设计参数，并将对应计算结果与整环足尺试验结果进行对比，验证了计算结果的准确性，从而为类矩形盾构隧道的设计提供了一定的理论支持［12-13］。对于盾构隧道衬砌结构的极限承载力研究，部分学者基于断裂力学或非线性力学理论，建立了圆形盾构隧道结构［14-15］全过程受力非线性数值分析模型，得到了相应的结构荷载‒响应曲线，解释了结构破坏机理和影响结构受力性能及承载能力的关键因素，部分学者还基于整环足尺试验结果对上述模型进行了正确性验证［15］。上述研究在一定程度上真实描述了特定条件下盾构隧道结构的受力全过程，对相应的盾构隧道结构性能点有一定预判性，但已有的数值分析大部分基于圆形盾构隧道展开。

基于现有的研究成果与非线性有限元理论，结合类矩形盾构隧道结构整环足尺试验，建立准确预测类矩形盾构隧道结构在极限工况下全过程受力破坏性能点的非线性数值模型。结合非线性数值模型分析结果，进一步了解不同结构型式及工程条件下类矩形盾构隧道结构受力全过程的力学性能，探究结构在不同工况下的承载能力及破坏机制，并对影响结构承载能力的因素进行敏感性分析，进而提出合理的结构破坏模式并确定影响衬砌结构承载能力的关键因素。最后，结合盾构隧道结构鲁棒性评价方法对相应的类矩形盾构隧道结构整体安全性进行简要评价。

1 极限承载力分析模型及相关参数

1.1 有限元模型及参数

基于类矩形盾构隧道结构整环足尺试验，采用有限元程序Ansys［16］，根据衬砌结构实际尺寸和构造，考虑结构几何非线性和材料非线性，建立了类矩形盾构隧道结构受力全过程非线性数值模型。关于材料非线性问题，对模型中的混凝土、主筋及接头螺栓材料赋予弹塑性本构关系，以模拟材料实际情况下的非线性本构关系。关于结构几何非线性问题，考虑管片结构大变形及接缝大转动等非线性结构位移对整体受力状态的影响。模型的外包尺寸为11 500 mm×6 937 mm，环宽为1 200 mm。全环由2块T 块（T1 和T2 块）、3 块C 块（C1、C2 和C3 块）、3块B 块（B1、B2 和B3 块）、1 块L 块、1 块F 块以及中柱（LZ）组成，管片厚450 mm，中柱宽度随工况不同而发生改变。块与块间接头形式为预埋钢套箱型接头，环向采用4 根螺栓进行连接。模型分为管片及中柱模型、刚域模型和接头模型，如图1所示。

1.1.1 管片及中柱模型

类矩形盾构隧道结构的管片和中柱均为混凝土结构，采用纤维梁单元［17］对管片和中柱进行模拟。纤维梁单元可将钢筋混凝土截面进行积分点分层处理，并对各层积分点赋予不同的材料属性，实现各层间的材料分离，可用于模拟不同材料如钢筋、混凝土等。模型中钢筋混凝土管片和中柱截面沿厚度方向划分为8 层，采用面积等效的方法将离散分布的受力主筋转化为沿管片宽度方向均匀分布的连续纤维。模型与整环足尺试验结构如图2 所示。第2 层和第7 层材料属性为钢筋，其他层材料属性均为混凝土。

上述试验结构的管片（中柱）混凝土材料本构关系如图3a 所示［15］。根据浇筑试验结构管片时的同期混凝土材性试验结果，抗压极限强度参数输入为44 MPa，极限强度对应的压应变为0.001 80。混凝土达到极限强度后，强度下降至50%时应变为0.002 72，最终混凝土残余强度为极限强度的45%，即20 MPa。管片（中柱）主筋材料本构关系如图3b所示［18］。图3b 中，曲线分为三个阶段：第一阶段为弹性阶段，定义弹性模量为200 GPa，屈服强度fy为400 MPa；第二阶段为钢筋的屈服阶段，当屈服平台结束时应变εsh为0.002；第三阶段为强化阶段，钢筋的极限强度fult为540 MPa，对应极限应变εult为0.020。

鉴于类矩形盾构隧道结构T块管片和中柱连接处截面加大、T块管片与中柱存在共同受力问题，采用刚域模型模拟受力特性。刚域是指自身不变形，但可发生刚体位移并且位移必须依附于构件而存在的一种理想化构件。

1.1.2 接头模型

类矩形盾构隧道结构管片间接头及管片与中柱间接头在轴力与弯矩的共同作用下发生张开与转动。对管片接头模型中接头进行简化，将接头的接触面假定为两块刚性板，刚性板没有质量且不产生变形，并与管片本体梁单元进行固接，能够适应接头处离散梁弹簧单元的变形，随之进行自由的刚体平动或转动。刚性板之间使用若干抗压弹簧单元与一根抗拉弹簧单元模拟混凝土之间的挤压作用与连接螺栓的抗拉作用，利用弹簧的拉压刚度和剪切刚度来模拟接头的实际转动和变形。采用离散梁弹簧单元对接头的宏观性能进行模拟，该单元可以用于模拟6个独立自由度的弹簧，将轴压力‒变形关系赋予不同自由度方向，进而在离散梁弹簧单元中定义各自由度方向变形与内力间的非线性本构关系，从而模拟纵向接缝的拉压、弯曲及剪切性能。管片间纵缝接头模型如图4 所示，中柱和T 块管片间接头模型如图5所示。

用于分析结构承载力的非线性数值模型仅限于平面内问题，而且整环足尺试验证明接头处环宽方向的拉压并不明显，故不考虑接头除转动及剪切外的其他变形，仅对接头间转动刚度和剪切刚度进行定义。

按实际情况设定梁弹簧单元的拉压‒变形曲线，根据混凝土和连接螺栓的实际受力，剪切刚度可设置为无穷小或无穷大，将其他自由度方向的刚度设置为无穷大。接头连接螺栓弹簧单元的剪切刚度设置为无穷大，抗拉刚度由螺栓材料应力‒应变关系转化得到的轴拉力与变形关系确定［19］，如图6 所示。模拟接头混凝土的弹簧单元只设置抗压刚度，抗压刚度由混凝土材料的应力‒应变关系转化得到的轴压力与变形关系确定［19］，如图7 所示。混凝土抗压强度采用同期混凝土材性试验结果，取56 MPa，接头处混凝土受力影响深度近似为2 倍截面受压区高度。

1.2 模型求解方法

包含几何非线性与材料非线性的有限元问题通常可归结为一个非线性方程组的求解问题，而非线性方程组的精确解往往难以直接求得。在相关有限元问题中，非线性方程组通常采用简单增量法进行求解。将每一级荷载增量下求得的状态变量视作平衡状态，由此计算对应的切线刚度矩阵用于下一级的计算，同时累计位移增量。该方法运算速度较快，但由于每一级荷载下的结构未进行校正，结构未达到平衡状态，会导致误差的累计，从而使得数值计算结果偏离精确解。

对简单增量法进行改进，将某一级荷载增量ΔFi-1=Fi-Fi-1下求得的荷载Fi处的不平衡力作为修正荷载，利用修正荷载对该级荷载增量下的状态变量进行校正，并利用校正后的荷载F′i及变形量δi计算对应的切线刚度矩阵。将此切线刚度矩阵用于下一级荷载增量ΔFi=Fi+1-Fi条件下的迭代计算，即一阶自校正增量法，求解过程如图8 所示。一阶自校正增量法具有较高的求解速度，同时也比简单增量法的计算精度高，在求解非线性问题特别是求解塑性问题时得到广泛应用。因此，采用一阶自校正增量法对非线性数值模型进行计算。

1.3 结构极限承载力分析指标

引入结构鲁棒性分析方法，对各因素影响下的类矩形盾构隧道结构的整体安全性进行评价，由此提出相应鲁棒性指标的定义。

广义超载系数K为基于承载力的鲁棒性指标，计算式如下所示：

式中：Fu为结构极限状态下的广义荷载；F0为设计广义荷载。

延性系数μ为基于延性的鲁棒性指标，计算式如下所示：

式中：μm为结构整体极限变形；μy为结构首次出现局部屈服时的整体变形。

极限工况下随着结构鲁棒性指标的提升，结构安全储备量不断提升。因此，引入广义超载系数K及延性系数μ对不同因素进行参数敏感性分析，不仅能够反映结构的承载能力及变形大小，还有利于进一步探讨各因素对结构整体安全性的影响。

2 基于整环足尺试验的模型验证

基于三组类矩形盾构隧道结构顶部超载极限工况下整环足尺试验结果，建立类矩形盾构隧道结构全过程受力分析模型，对类矩形盾构隧道结构进行数值分析并基于数值计算结果对不同工况下的结构极限承载力进行分析。

2.1 整环足尺试验

类矩形盾构隧道顶部超载极限工况整环足尺试验模拟的是，真实受力状态下类矩形盾构隧道结构顶部出现意外堆载而导致结构发生破坏的过程，从而了解极限工况下结构薄弱部位和影响结构承载力的主要因素。

针对类矩形盾构隧道结构共进行三组整环足尺试验（第一环试验、第二环试验和第三环试验），试验所采用的类矩形盾构隧道结构如图9所示。几何尺寸及材料选用与有限元模型基本相同。全环由2块T块、3块C块、3块B块、1块L块、1块F块以及中柱组成，试验过程中对各块管片进行编号，具体编号方式如图9 所示。中柱宽度固定为350 mm。各组试验结构包含10个纵向接头，并设顶部T1块与C1块管片间的纵向接缝为1号纵向接缝（编号为JF1），后顺时针依次将纵向接头编号为JF1―JF10，各纵向接头采用4 根6.8 级M33 型螺栓进行连接。管片所用混凝土等级为C50，钢筋为HRB400 热轧钢筋。管片配筋、T块管片箍筋形式和连接螺栓位置如表1所示。因第二、三环试验结构的设计埋深较第一环试验结构大，故第二、三环试验结构的主筋配筋率较第一环试验结构而言提升56.3%。第三环试验结构在第二环试验结构的基础上针对结构薄弱部位进行了补强，即对T 块管片抗剪配箍和环缝接头连接螺栓位置进行了优化，第三环试验结构环缝接头连接螺栓位置根据接缝弯矩正负性进行移动，正弯矩接头向内弧面移动50 mm，负弯矩接头向外弧面移动50 mm［4］。

表1 三组试验结构管片配筋及螺栓位置情况Tab.1 Reinforcement and bolt position of three tested rings

三环管片足尺试验通过30 个点对称集中荷载进行加载，分为P1（8个加载点）、P2（10个加载点）、P3（12个加载点）三组，如图10所示。加载过程中各组加载点处同步施加相同大小的荷载。试验前对实际受力条件及加载条件下的试验结构内力进行预分析，通过控制截面处内力等效的方式，对各组加载点在各阶段施加的荷载值进行了设计［4］，数值模拟中的加载制度与整环足尺试验所采用的加载制度相同。

2.2 基于整环足尺试验的模型验证

根据上述建立的类矩形盾构隧道结构全过程受力非线性数值模型对三组试验结构分别进行数值模拟，将计算结果与整环足尺试验结果进行对比，验证模型的正确性和有效性。

2.2.1 结构破坏过程验证

三组试验结构的整环足尺试验与数值模拟破坏过程对比如图11所示。由图11可知，三组试验结构的试验结果和数值模拟破坏过程均呈现为三个阶段，即弹性阶段、带裂缝工作阶段和屈服阶段。弹性阶段是指结构处于弹性受力状态，在此阶段进行卸载，结构能够恢复至初始状态，无塑性变形产生，定义弹性荷载点为该阶段终点；带裂缝工作阶段是指随着结构荷载逐渐增大，管片本体或纵向接缝处混凝土达到受拉或受压峰值应力，混凝土产生裂缝后的结构受力阶段；屈服阶段是指管片本体某一截面或某纵向接缝处同时发生混凝土压碎、钢材屈服，结构首次出现塑性铰后的受力阶段，定义屈服点为该阶段起点；此外，定义结构发生整体失稳或体系转变的时刻为极限荷载点，结构加载至该性能点时无法继续承载。试验及数值模拟结果显示，第三环试验结构异于前两环试验结构，衬砌结构中出现T 块管片截面钢筋屈服、管片本体形成塑性铰现象，结构在屈服阶段的变形能力进一步增强，荷载‒变形曲线出现了较明显的平台段。

基于整环足尺试验结果，选取前述三个特征荷载点进行结构性能及极限承载力的分析及模型验证，对比结果如表2所示。

从表2 可以看出，三组试验结构整环足尺试验和数值模拟的破坏过程中，结构达到正常使用极限状态时的对应荷载值基本一致，但数值模拟的屈服点较试验结果晚；两者极限荷载点基本一致，但数值模拟极限变形值稍大；此外，结构的鲁棒性指标值大小相近。对比验证结果表明，该模型能准确地模拟类矩形盾构隧道结构在极限工况下的全过程受力，对结构破坏过程的性能点及极限承载力预测基本准确，同时该模型能够有效体现结构的整体安全性，适用于结构的极限承载力分析。

2.2.2 连接螺栓应变验证

三组试验结构整环足尺试验与数值模拟的连接螺栓应变对比如图12 所示。三组试验结构连接螺栓应变随荷载发展规律的数值模拟和整环足尺试验结果基本吻合，连接螺栓应变的拐点较为一致，螺栓屈服情况和试验结果也基本相同。

从图12可知，数值模型能准确模拟三组试验结构管片间接头和连接螺栓的受力性能。同时，采用非线性数值模型计算得到的结构破坏过程避免了由于试验分级加载导致的性能点跳跃问题，更加精确地得到结构破坏过程的受力路径，可作为类矩形盾构隧道结构极限承载力分析的重要研究手段。

3 结构极限承载力参数分析

类矩形盾构隧道作为一种新型盾构隧道结构型式，由于其与常规圆形隧道有一定的差异，影响此型式结构极限承载力的因素可能与影响常规圆形隧道的有所差别，因此利用该数值模型针对整环足尺试验中反映出的结构薄弱环节进行参数分析，有利于探寻影响结构极限承载力的关键因素，并以此为依据对结构进行针对性调整，从而提升结构的极限承载力及整体安全性，为实际工程设计提供优化方案。

表2 整环足尺试验及数值计算的破坏过程性能点比较Tab.2 Comparison of performance points between full-scale test and numerical simulation during whole failure process

3.1 工况选取

由整环足尺试验结果可知，纵向接头和T 块管片是类矩形盾构隧道结构的薄弱环节，也是影响结构受力性能的主要结构因素。接头的受力性能主要与结构的构造形式和连接螺栓有关，管片的受力性能主要与管片本体的强度与刚度有关。因此，确定的关键因素包括连接螺栓位置、连接螺栓强度、管片配筋量、中柱刚度。针对各关键因素设置不同的计算工况，具体计算工况如表3所示。

表3 工况汇总Tab.3 Summary of conditions

3.2 连接螺栓位置参数分析

类矩形盾构隧道结构在正常运营工况下纵向接头弯矩正负性明确，根据接头弯矩正负性调整连接螺栓位置，可更加充分发挥接头受力性能。鉴于整环足尺试验无法分析螺栓位置对结构承载能力的影响规律，因此结合类矩形盾构隧道结构全过程受力非线性数值模型，研究极限工况下正弯矩接缝处连接螺栓向内弧面、负弯矩接缝处连接螺栓向外弧面分别移动30、40、50、60、70 mm 时结构承载能力的变化。

根据数值计算结果，以P1作为广义荷载，得到不同接头连接螺栓位置衬砌结构破坏过程，如图13所示。

由数值模拟结果可知，螺栓位置优化后结构破坏源于纵向接头破坏。螺栓位置移动距离不同，接头连接螺栓屈服顺序有所不同。当螺栓移动距离为30 mm 时，腰部JF8 号接缝螺栓屈服晚于中柱附近JF6 号接缝螺栓；随着螺栓移动距离增大，腰部JF8号接缝螺栓屈服顺序提前而中柱附近JF6号接缝螺栓屈服顺序延后，即接头刚度增加后腰部接缝处负弯矩增长较快，内力向腰部集中，破坏源头也向腰部移动。

由数值模拟结果得到的不同连接螺栓位置衬砌结构对应的鲁棒性指标如表4所示。由表4可知，螺栓位置移动30 mm 至70 mm 过程中，结构广义荷载系数对应提升3.2%、2.9%、3.2%、2.0%，延性系数对应提升7.8%、11.7%、16.3%、12.4%。这说明，接头螺栓向拉应力区移动后，结构鲁棒性指标不断提高，结构承载能力与安全储备量不断提升。

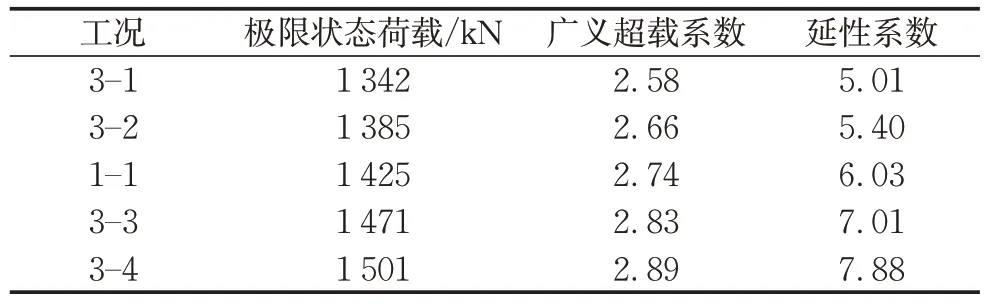
表4 不同连接螺栓位置衬砌结构鲁棒性指标对比Tab.4 Comparison of robustness indexes of lining structure between different bolt positions

随着荷载的提升，结构最终均发生延性破坏，主要表现为两种形式：当螺栓位置移动距离小于50 mm时，接头极限承载力提高幅度有限，结构最终破坏时管片本体未形成塑性铰；当螺栓位置移动距离不小于50 mm 时，接头极限承载力得到了较大幅度提升，受力过程中部分接头受压混凝土首先开裂，接头相继形成塑性铰，随之产生的结构内力重分布现象促使管片本体主筋屈服，管片本体形成塑性铰直至结构发生破坏，在此破坏形式中管片本体的受力性能得到更充分的发挥。

结合前述现象进一步说明，接头本身承载力较低时，结构极限承载力的提高主要由于接头优化而使得接头本身承受更多内力，进而保证管片本体受力性能得到充分发挥，因此随着接头螺栓位置的优化，结构鲁棒性指标不断提高；管片本体受力性能充分发挥后，结构极限承载力的提高主要由于接头优化而使得纵向接头本身承受更多内力，因此结构极限承载力及结构延性提升幅度在连接螺栓位置移动60 mm以上时有减小的趋势。接头螺栓位置的优化需要与管片本体承载力相匹配，提升结构承载能力的同时需要避免结构在接头破坏后发生脆性破坏。

3.3 连接螺栓强度参数分析

为保证结构安全，在结构设计中需选择适当强度的螺栓进行校核验算。结合类矩形盾构隧道结构全过程受力非线性数值模型，选择结构设计中常用的螺栓强度等级，包括5.8 级、6.8 级和8.8 级螺栓，研究极限工况下连接螺栓强度对结构受力性能的影响。

根据数值计算结果，以P1作为广义荷载，得到不同连接螺栓强度衬砌结构破坏过程，如图14所示。

由数值模拟结果可知，结构的最终破坏机理与极限承载力和接头极限承载力相关，主要表现为两种形式：当螺栓强度较小时，接头极限承载力较小，结构最终破坏时管片本体未形成塑性铰；当螺栓强度较大时，接头极限承载力相应提高，管片本体最终形成塑性铰，管片本体受力性能得到更充分发挥。换而言之，当接头极限承载力足以使管片本体发挥承载力时，结构极限承载力的提高主要由于接头承载力提高而使得接头本身承受更多内力。

不同接头连接螺栓位置衬砌结构对应的结构鲁棒性指标如表5所示。由表5可知，随着接头连接螺栓强度提高，结构极限承载力及鲁棒性指标不断提高，结构承载能力及对应整体安全性提升。具体而言，接头螺栓强度等级由5.8 级提升至6.8 级时，强度提高20%，对应结构广义超载系数提高8.3%，延性系数提高16.2%；强度等级由6.8级提升至8.8级时，强度提高33%，对应结构广义超载系数提高9.8%，延性系数提高5.1%。随着螺栓强度增加，结构受力性能得到优化，极限承载力及安全储备量逐步提升，但相比于螺栓强度的提高，结构安全储备提升幅度减小。另外，对不同工况下结构受力全过程的对比发现，选用6.8 级与8.8 级的接头螺栓时，管片本体钢筋屈服点荷载基本一致，并且管片本体最终均形成塑性铰，说明上述两种工况下，管片本体的受力性能均已充分发挥。

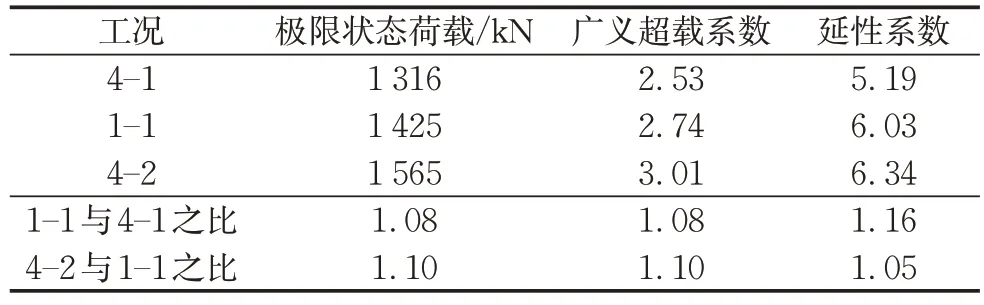
表5 不同连接螺栓强度衬砌结构鲁棒性指标对比Tab.5 Comparison of robustness indexes of lining structure between different bolt strengths

接头螺栓强度的变化对结构破坏机制、承载能力及安全储备有较为显著的影响，采用提高螺栓强度措施对类矩形盾构隧道结构的受力性能进行优化效果较佳。然而，随着螺栓强度的不断提升，结构安全储备量提升幅度减小，故同样需要注意螺栓强度和结构整体受力性能的匹配。

3.4 管片配筋量参数分析

类矩形盾构隧道结构在不同管片配筋率条件下均有应用，而配筋量的不同会大大影响结构的受力性能。现有的整环足尺试验结果无法对其影响进行充分考虑，故需要结合类矩形盾构隧道结构全过程受力非线性数值模型，研究极限工况下接头连接螺栓位置优化前后管片配筋量对结构受力性能的影响。

根据数值计算结果，以P1作为广义荷载，得到接头连接螺栓优化前后不同管片配筋量衬砌结构破坏过程，如图15所示。螺栓位置优化前后不同管片配筋量衬砌结构对应的鲁棒性指标如表6所示。接头连接螺栓位置优化前，不同配筋量的结构荷载‒变形曲线基本一致。由于接头螺栓位置未优化，接头承载能力较小，最终的结构破坏机制是接头相继形成塑性铰，促使结构内力重分布，导致管片本体破坏，最终结构失去承载力。此时影响结构极限承载力的控制条件是接头承载力，管片本体配筋量增长56.2%后结构广义超载系数仅提高1.8%，配筋量的改变并非影响结构破坏过程及导致极限承载力变化的敏感因素；管片本体配筋量增长56.2%后结构延性系数仅提高6.3%，同样说明配筋量的提升对结构安全储备量的影响较小，即影响结构极限承载力的控制条件为接头承载力时，管片配筋量对结构受力性能影响不明显。

接头连接螺栓位置优化后，结构的荷载‒变形曲线发展出现明显差异。在管片本体钢筋屈服前，两种工况下的结构荷载‒变形曲线基本一致。管片主体钢筋屈服后，工况2‒3 中由于管片本体配筋量较少，结构变形发展较快，接头受力提前促使连接螺栓迅速进入屈服阶段。随着T2块管片受拉钢筋屈服、受压侧混凝土压碎及受压钢筋屈服，结构内力重分布导致纵向接头迅速形成塑性铰进而导致结构失效。影响结构最终破坏机制与极限承载力的控制条件为T 块管片本体承载力。工况1‒1 中，管片配筋量增加，管片本体承载力提高，管片本体破坏前接头受力性能得到充分发挥，最终的结构破坏机制为管片本体形成塑性铰导致结构失效，影响结构最终破坏机制的主要因素为管片本体承载力。不同配筋量结构破坏过程的最大区别在于管片本体和纵向接头形成塑性铰顺序，管片配筋量增加56.2%时，管片本体承载力能保证纵向接头受力性能充分发挥，结构广义超载系数提高16.0%，延性系数提高14.9%，表明接头承载力与结构受力性能匹配时，提高管片配筋量能够充分发挥管片本体及接头的承载力，进而明显提升结构极限承载力与安全储备量，优化结构受力性能。

表6 不同管片配筋量衬砌结构鲁棒性指标对比Tab.6 Comparison of robustness indexes of lining structure between different reinforcements

综上，当衬砌结构最终破坏取决于接头极限承载力时，管片本体配筋量对结构破坏模式及受力性能的影响较小，管片配筋量可优化；当衬砌结构最终破坏取决于管片本体受力性能时，管片本体配筋量对结构承载能力的影响较大，管片配筋量提高可优化结构破坏模式、提升结构受力性能及安全储备。因此，与结构破坏机制和受力性能匹配的最优管片配筋量应能保证结构接头相继形成塑性铰的同时管片本体发生抗弯破坏。

3.5 中柱刚度参数分析

中柱是类矩形盾构隧道结构重要构件，而整环足尺试验中并未分析中柱的刚度变化对类矩形盾构隧道结构受力性能及极限承载力等的影响规律，故结合类矩形盾构隧道结构全过程受力非线性数值模型，通过不同中柱宽度设置对不同中柱刚度衬砌结构进行计算，研究极限工况下中柱刚度对结构受力性能的影响。

根据数值计算结果，以P1作为广义荷载，得到不同中柱刚度衬砌结构破坏过程，如图16所示。

由图16可知，中柱刚度的变化对结构破坏机制有一定的影响。对于工况5‒1 而言，由于中柱刚度较小，在极限荷载作用下，结构顶底收敛变形量较工况1‒1 有59.6%的增长；与此同时，中柱刚度过小时，结构顶底接头处承受的内力有显著提升，这导致加载过程中接头相继形成塑性铰而促使结构破坏，结构最终破坏时管片主筋未出现屈服现象，结构产生脆性破坏。中柱宽度不小于700 mm时，结构破坏过程趋近一致，接头受力延后，相继形成塑性铰后管片主筋出现屈服现象，管片本体最终形成塑性铰，结构整体失去承载力，产生延性破坏。然而，随着中柱刚度的进一步增大，中柱对顶底管片产生更大的约束，管片本体处内力进一步增长而接头处内力有所降低。随着中柱刚度的增大，接头连接螺栓屈服延后，管片本体则提前进入屈服阶段，结构破坏时间提前，如工况5‒2较工况1‒1结构破坏时极限变形减小14.6%、工况5‒3较工况5‒2结构破坏时极限变形减小8.2%等，这和牺牲变形以减小内力的响应规律一致。

不同中柱刚度衬砌结构对应的鲁棒性指标如表7所示。由表7可知，工况5‒1中结构广义超载系数较其他工况有8%～9%的降低，而延性系数的最大降幅达到了44.6%，说明中柱刚度过小时，衬砌结构承载能力较差、安全储备量不足。随着中柱刚度的增长，结构广义超载系数及延性系数有先增长后略微减小的趋势，进一步证明中柱刚度的增长在一定程度上能够提升结构的承载能力并使得结构具有更多的安全储备量，但中柱刚度过大时，反而对结构的受力性能有一定程度的削弱。因此，实际工程中应注意中柱刚度和结构受力性能匹配，确保结构拥有最佳的承载能力及较多的安全储备。

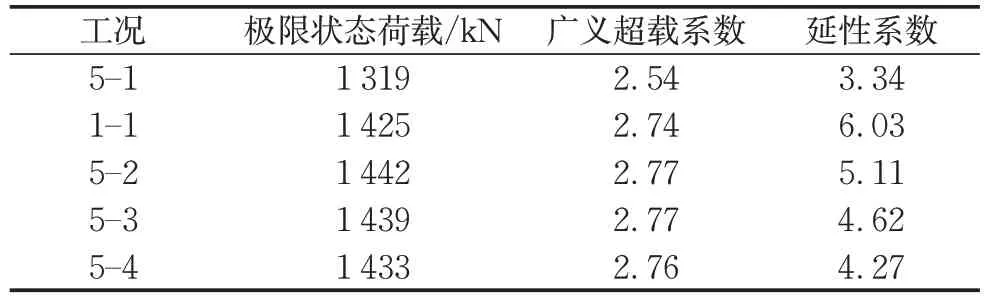
表7 不同中柱刚度衬砌结构鲁棒性指标对比Tab.7 Comparison of robustness indexes of lining structure between different interior column stiffnesses

3.6 管片厚度参数分析

对于盾构隧道而言，调整管片厚度是在确保结构具有良好受力性能的前提下控制施工成本的重要途径，将管片厚度减薄能够有效减少投入生产的材料用量及对应的材料费用。结合类矩形盾构隧道结构全过程受力非线性数值模型，对管片减薄后的结构进行计算，从而研究极限工况下管片厚度变化对结构受力性能的影响。

对管片厚度减薄后的结构进行受力全过程数值模拟，其中接头弹簧刚度按照管片厚度进行等比例放缩，根据数值计算结果，以P1为广义荷载，得到管片减薄及增加配筋后的衬砌结构破坏过程，如图17所示。

由图17可知，管片厚度减薄后，结构的荷载‒变形曲线发展出现明显差异。在设计工况下，管片厚度减薄导致结构的整体刚度下降，在管片本体钢筋屈服前，管片减薄后的衬砌结构变形发展较快。与此同时，管片减薄导致管片本体及管片接头处的混凝土受压区高度降低，纵向接头螺栓及管片本体钢筋提前进入屈服阶段并且塑性铰出现时间提前；管片减薄后衬砌结构未出现明显的塑性阶段，延性有明显的降低，并且提升配筋量无法弥补不利影响。此外，模拟结果显示，工况6‒1 中管片T2 块产生局部抗弯破坏而导致结构失效，即管片减薄后若不针对结构薄弱部位进行增加配筋量等补强处理，大部分纵向接头的受力性能难以得到充分发挥，衬砌结构受力的整体性被削弱，同时造成纵向接头处材料的浪费。配筋对应增加后，衬砌结构的破坏模式较为合理，呈现结构整体破坏的形式。荷载加载至极限荷载点时，大部分纵向接头形成塑性铰，结构转变为瞬变机构从而失去承载力，此时T 块管片并未发生局部破坏现象，各接头的承载能力得到了更充分的发挥。因此，建议管片减薄后需要增加管片本体的配筋量，以确保衬砌结构有较好的整体受力性能及合理的破坏机制。

管片减薄及配筋量优化后的衬砌结构鲁棒性指标如表8所示。

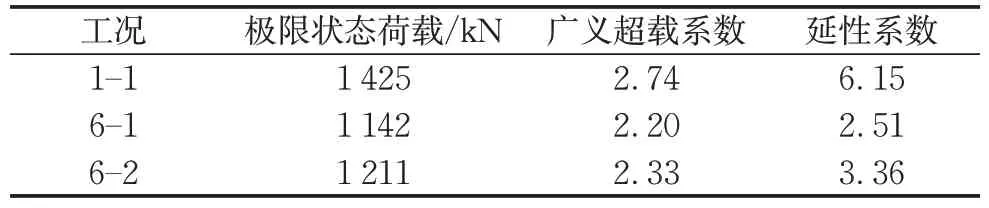
表8 管片厚度减薄并优化后衬砌结构鲁棒性对比Tab.8 Comparison of robustness indexes of lining structure between different thicknesses of segments

由表8 可知，管片厚度减薄后广义超载系数有19.9%的降低，而且延性系数降低较多，降幅达到59.2%；增加配筋量后，结构广义超载系数有6.0%的提升，延性系数的增幅为33.9%。由此说明，虽然管片本体配筋量的增加使得衬砌结构破坏模式得到了改善，结构从局部抗弯破坏向整体破坏转变，但是由于管片厚度减薄削弱了接头极限承载力，衬砌结构的承载能力及安全储备量仍不能得到较大的提升。因此，衬砌结构的管片厚度减薄后，采用增加配筋量的方式改善结构的破坏模式是必要的，但在提升管片配筋量的同时，需要对纵向接头进行优化设计，合理提升接头极限承载力并保证其与管片本体的受力性能相互匹配，在确保破坏模式不发生改变的同时提升衬砌结构整体的承载能力与安全储备量。