基于超点图的点云实例分割方法

王志成，余朝晖，卫 刚，孙 雨

（同济大学CAD研究中心，上海201804）

点云是一种重要的三维数据表示形式，数据保存时每一个点由坐标加上该位置上的值构成。因为点云的存储形式具有不规则、无序性以及数据抽象和难以可视化等特点，因此点云处理面临着巨大的挑战。传统方法在处理点云数据时存在着精度低、算法泛化能力差等问题。随着深度学习在二维图像任务如识别、检测以及分割上取得巨大突破，学者们开始探索将神经网络运用到点云处理上并取得重大的进展。

将深度学习算法应用到点云处理上的最直接方法是先将数据转换为体素化模型［1］，也就是三维结构化数据，然后直接用三维滤波器来训练一个卷积神经网络，如应用于自动驾驶的全卷积网络模型［2］。然而，该方法使体积数据变得庞大，训练数据以及卷积核由二维变成三维，这意味着需要大量的计算，现阶段的计算能力难以达到要求。还有一些方法采用多视图数据，比较经典的就是基于多视角的三维目标检测网络［3］。Charles 等［4］提出了第一个直接处理点云数据的神经网络算法PointNet，将点云数据投影到二维平面。该方法不直接处理三维的点云数据，而是先将点云投影到某些特定视角。许多研究对PointNet特征提取方式进行改进，如PointCNN［5］，通过一种自定义的X‒Conv 操作，使常规的Convolution 也能处理点云。Jiang 等［6］提出了PointSIFT 模型，对于每一个点云能端对端地输出一个表征向量，该向量编码了各个方向的信息，同时自适应地选择合适的表征尺度。目前，对于深度学习在点云数据实例分割中的运用已经有了进展，相似度分组网络（SGPN）［7］模型是第一个直接学习三维点云特征的实例分割网络框架。使用PointNet提取特征，通过一个单独网络去预测点组推荐并为各个推荐组分配相应标签；采用深度相似矩阵表征特征空间中每对点之间的相似性，进而产生点分组建议。

现阶段点云实例分割并不能达到理想的效果，各种算法还有待提升。提出了一种基于超点图的点云实例分割（ISPG）方法，旨在提高实例分割任务的精度和效率，并且在实验中验证方法的有效性。

1 基于超点图的点云实例分割方法

为了处理无序的、不规则的点云数据，提出将大场景三维点云用一系列相互联系的简单形状构成超点的表达方式，这种表达方式与影像分割中的超像素类似，由一种称为超点图（SPG）［8］的属性有向图结构描述。超点图的节点表示简单的结构，而富有边特征的边描述了它们的连接关系。

超点图的表达方式有以下几个显著优点：

（1）超点图将目标的分割部分作为一个整体，而不是对单个点或者体素进行分类，部分点的整体—超点具备比单个点或者体素更加显著的特征，有利于后续的实例分割。

（2）超点图可以详细描述相邻目标之间的位置关系，这对于上下文分类至关重要，如车辆通常是在道路上、天花板由墙面包围等。

（3）超点图的大小由场景中简单结构的数量决定，相比于处理之前的点集或者体素，超点图在数据量上要小得多。因此，可以对长距离的交互进行建模，而这在没有强假设的成对连接中是很难实现的。

1.1 超点划分

算法将点云划分成几何上简单且有意义的形状，称之为超点。算法的目标不是检索单个对象，如汽车或椅子，而是将对象分解为简单的几何部分。对于聚类的结果，不仅要求在几何上是简单的，还期望在语义上是同质的，也就是每个几何形状不覆盖不同类的对象。在超点图的网络中，将整个点云作为算法的输入，从点云分区可以很容易地计算出超点图。为了提高效率，这里使用了全局能量模型。

输入点云C 是n 个点的集合，每个点由包含（x，y，z）的位置信息和其他观察值定义，如颜色和强度等。对于每个点，将一组几何特征ρ 作为局部特征。在本研究中，使用了文献［9］中提出的三个特征描述符，包括线性、平面性和反射强度，以及文献［8］中引入的垂直度特征。特征描述符是由邻域定义的，对于每个点的邻域，一组点的坐标的协方差矩阵的特征值分别为 λ1、λ2、λ3，规定 λ1≥λ2≥λ3。特征描述符的计算式如下所示：

式中：ρl表示线性度；ρp表示平面度；ρs表示散射值。线性度描述了邻域的连续程度，平面度评估了邻域点对于平面的拟合程度，散射值反映了各向同性和曲面度。在实验中，垂直范围被证明对区分道路和墙壁，以及具有相似尺寸的电线和电线杆至关重要。因此，还使用了垂直范围分量η这个描述子。设u1、u2、u3是分别与λ1、λ2、λ3对应的三个特征量。将垂直范围分量定义为特征向量各维度绝对值的加权和的近似，权重为对应的特征向量的值，计算式如下所示：

式中：uk表示单位化的特征向量。点云的空间结构可以由无向图Gu=(V，E)表示，其中节点V代表点云的点，边E 代表节点间的邻接关系。全局能量模型［9］由距离每个点最近的n 个点定义，使用无向图Gu=(V，Enn)，Enn表示最近的n个点的平均距离，算法的n取10。该几何分区的问题被定义为以下能量泛函的极值问题：

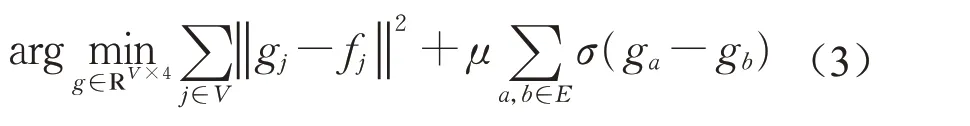
式中：g 表示拟合既定特征；f 表示点的几何特征，包含四个维度（ρl，ρp，ρs，η)；μ表示正则化系数，作用是保证分割的形状足够简单；σ 为激活函数。该方法不仅可以达到有效逼近l0‒cut 算法的效果，还具有自适应的效果。在几何形状变得复杂时，超点中包含的点的个数将下降，反之将上升。

1.2 超点图定义

在第1.1 节中得到超点后，使用有向图Go=(S，E，ω)表示整个点云，并命名为超点图。S是所有超点的集合，S={S1， }S2，S3，… ，其中Si表示一个超点的点集；E表示超点之间的邻接关系，命名为超边，E={E1， }E2，E3，… ，其中Ei表示超边；ω表示编码超点图边界的权重。Ε表示无向图中所有边的集合，如果图上有一条边将超点连接在一起，则将两个超点定义为相邻，表达式如下所示：

式中：ωs，t表示（s，t）连接的个数。

超边示意图如图1所示。点之间的边用实线表示，部分超点分割之间的邻接用虚线表示。

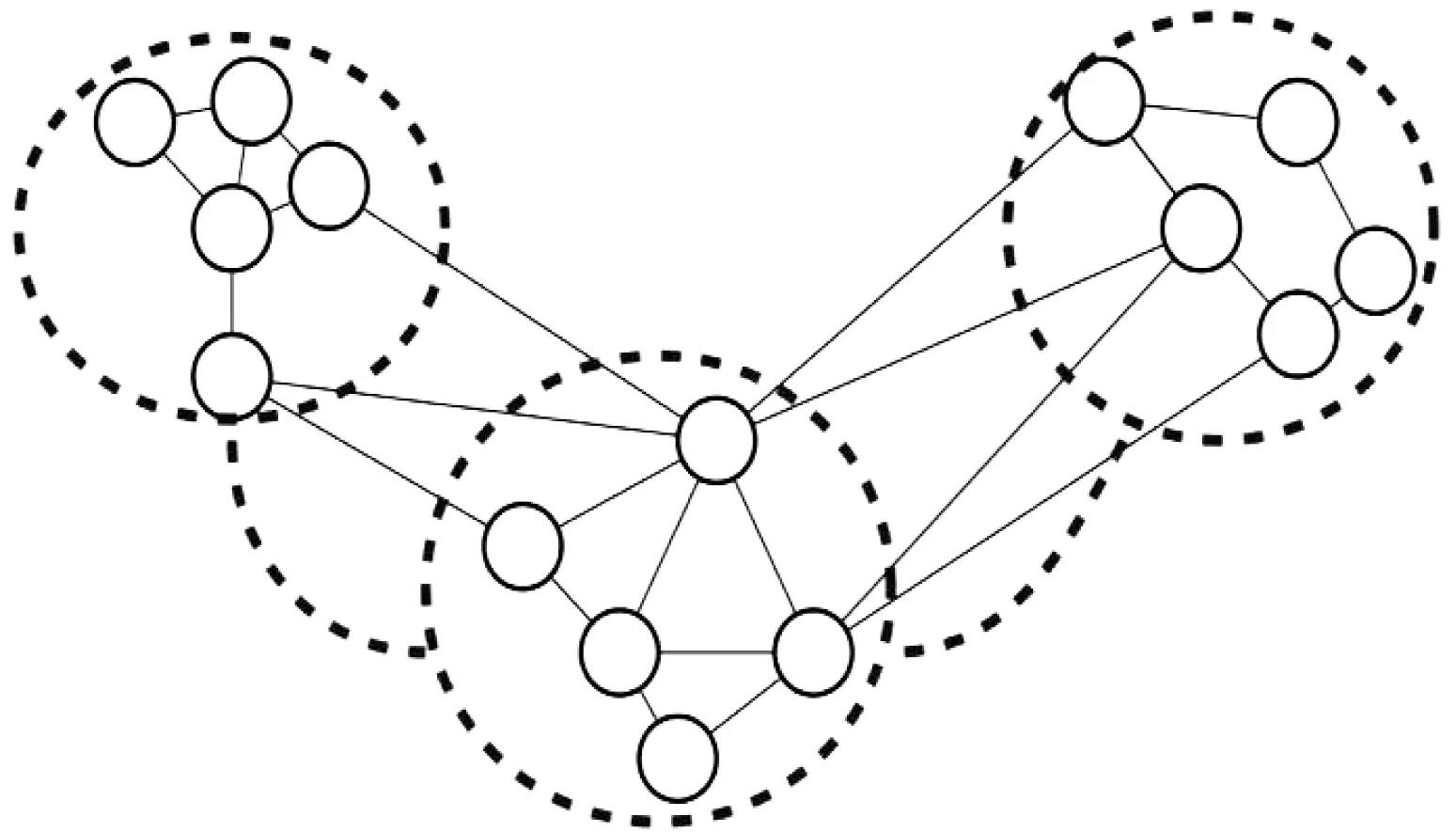
图1 超边Fig.1 Superedge

超边还可以通过比较相邻超点的形状和大小来定义特征。用|S|表示超点S包含的点数。此外，还定义了长度L=λ1、表面积A=λ1λ2和体积v=λ1λ2λ3等形状特征。λ1、λ2、λ3是每个超点中点的坐标的协方差矩阵的特征值，按递减顺序排序。表1描述了超边特征，p表示一个超点。

表1 超边描述子及定义Tab.1 Superedge descriptors and definitions

1.3 超点嵌入

将超点转化为固定维度的向量表示。每个超点的转化都是独立进行的，超点所需要的上下文信息从第1.4节中获取。

选取PointNet 作为超点嵌入算法模型。PointNet 网络简单，并且具有很好的鲁棒性和较高的效率，在实验中表现出不俗的性能，具体流程如图2所示。在PointNet中，输入点首先由空间变换网络（STN）［10］实现对齐，然后由多层感知器（MLP）独立处理，最后用最大池化提取到全局特征。图2 中，np表示每次输入的节点数，dp表示特征维度，dz表示输出的特征维度。

图2 超点嵌入Fig.2 Superpoint embedding

在超点的处理中，使用更为简洁的PointNet 完成嵌入，一定程度上节省了在门控循环单元（GPU）上评估时的内存占用。具体做法：首先对超点进行采样，训练时点的个数小于40的超点将影响训练效果，因此对此类超点的分类将依据上下文信息进行判断。

为了使PointNet学习不同形状的空间分布，在处理之前需要将每个超点都重新缩放到单位球面范围内。因此，每个点由归一化后的位置信息p′j、观测信息oj以及几何特征fj描述。此外，原始矩阵的缩放尺度将作为一个额外特征连接到最大池化后得到全局信息。

1.4 上下文语义中的分割

Pipeline 的最后一步是根据嵌入和超点图中的局部特征对超点进行分类。基于之前建立的超点图模型，采用图卷积来做最后的处理。

根据超边的信息改善超点的嵌入。具体来说，每个超点si都在GRU 中保留其隐藏状态。隐藏状态初始化为嵌入，之后保留的是每轮迭代的结果。在迭代中，一个GRU 单元（见图3）将其隐藏状态和传入信息作为输入，并计算一个新的隐藏状态。对超点si，传入信息是和超点si邻接的超点的隐藏状态的加权和。

图3 GRU模块Fig.3 GRU module

GRU由一系列线性以及非线性计算组成，GRU的前向传播过程如下所示：

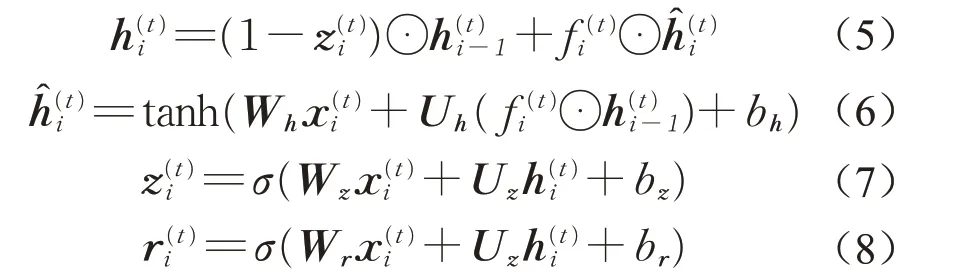
式中：x(t)i为输入；h(t)i为输出；⊙为矩阵点乘运算；ĥ(t)i为隐藏状态；σ(∙)为sigmoid函数；z(t)i为重置门输出矩阵；r(t)i为更新门输出矩阵；W、U和b为GRU中共享的可训练参数。式（7）和式（8）中出现了GRU的两个组件，即重置门z(t)i和更新门r(t)i。为了提高训练的稳定性，对式（7）和式（8）在线性变换后采用归一化操作，定是一个常数。

GRU 具有基于隐藏状态对输入进行加权的能力。例如，如果GRU的类别状态非常确定，GRU就会自动忽略上下文，或者只关注特定的特性通道。在输入之前乘上隐藏状态的权重，通过设置这些权重可以控制消息。

边缘条件卷积在模型中起着至关重要的作用，通过多层感知机处理连续序列的特征Fji动态生成过滤权重。多层感知机对权重矩阵进行回归，这一操作需要对每个边向量进行矩阵向量乘法，带来大量的额外计算量，增加了运行时间、访存以及参数量。为了减少计算量，只对特定于边缘的权重向量进行回归，并进行逐元素乘法，然后与GRU更新规则结合使用，使得通道混合被推迟。通过简化，边缘非特定方式的性能已达到与边缘特定方式相似的水平。尽管感知机没有明确S型激活函数，但逐元素乘法可以选择学习来充当边缘条件门。受到DenseNet［11］的启发，将所有迭代过程中的隐藏状态串联起来，并进行线性变换，以生成稠密特征yi。多层感知机在时间迭代中是共享的，定义为WO，表达式如下所示：

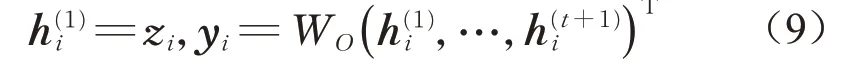
2 算法流程

ISPG模型如图4所示。算法分为以下三个步骤：

（1）按照几何形状均匀分区

将点云划分为几何上简单且有意义的形状，称之为超点。这一步骤完全是无监督的，分割出来的简单形状可以是大型的形状如道路或墙壁，也可以是更小的组件，如汽车或椅子的零件。

图4 ISPG模型Fig.4 ISPG model

（2）超点的嵌入

超点图的每个节点对应整体点云的一小部分，也就是对应几何形状简单的基元。假设超点在语义上是齐次的，将这些超点基元降采样到最多数百个点来表示。小尺寸点云可使用PointNet方法处理。

（3）邻域点云的分割

超点图的数量级比建立在原始点云上的任何图都小，基于图卷积的深度学习算法使用超点的边缘特征对这些节点进行分割，从而实现语义的分割。

3 实验

基于ScanNet［12］数据集、斯坦福大型三维（3D）室内空间数据集（S3DIS）［1］以及KITTI 数据集评估算法。此外，评估指标是基于原始点云计算的，而不是基于超点。使用tensoflow 神经网络框架和单个Nvidia GTX1080 Ti GPU进行实验。

3.1 超点质量

从图5 的可视化结果可以看出，全局能量模型可以很好地对稠密特征和稀疏特征的物体进行自适应分割。几何形状比较复杂的物体，如桌子、书架等（样本1和样本3），在较小的尺度内被分割成较多超点；墙、地板和天花板等物体（样本2），在特征空间内的距离很近，因此被分割成较为完整的超点。

3.2 对比实验设置

将分割结果与以下两种方法进行比较：

（1）簇分割（Seg‒Cluster）模型

该模型在与SGPN［12］模型相关的论文中首次提出，采取一种贪婪策略对点云进行简单分割。使用PointNet 网络执行语义分割，然后选择所有点作为种子。从种子点开始，利用广度优先搜索具有相同标签的邻居。如果找到的群集超过200 个点，就将其视为有效群组，然后采用分组合并算法合并有效组群。

（2）SGPN（PointNet）模型

SGPN模型中使用单个网络来预测点云的聚类区域及每个区域对应的语义类别。因此，该方法可以直接提取实例分割的结果。

3.3 ScanNet数据集测试结果

在ScanNet数据集上对18种常见对象类别进行评估和比较。原始点云作为输入，目标是分割场景中属于18 个对象类别的每个实例及其语义标签。IoU（αIoU)阈值为0.5 的平均精度（βAP）用作评估指标，αIoU和βAP的计算式如下所示：

式中：NTP、NFP、NFN分别表示预测正确、预测错误、没有预测到的物体数目。

图5 全局能量模型生成超点Fig.5 Superpoints produced by global energy model

如表2 所示，ISPG 模型的平均精度在大多数对象类别上的表现都超过了SGPN 模型。由于ISPG模型只需要捕获相对简单的对象分布就可以生成非常高质量的候选群组，因此可以针对几何变化较小的类别获得很高的精度。对于在分割过程中需要稠密信息的类别（如门、窗），SGPN模型无法获得良好的评分，因为它们的相似性度量无法有效地被编码；ISPG模型在这些类别上获得了更好的结果，这表明在生成候选群组时产生的特征更有利于分类。

图6 为SGPN 模型与ISPG 模型之间的定性比较。SGPN模型需要在学习的相似性度量空间中划出清晰的边界来区分对象实例，可以观察到许多对象包括一个对象的部分或多个对象的预测。与SGPN模型相比，ISPG模型生成的对象具有更高的针对性，从而带来了更好的细分质量。当存在大量背景点时，SGPN 模型很难学习良好的相似性度量标准，因为其仅专注于前景点的语义和相似性的学习，并且在训练过程中忽略了背景点，因此增加了基于背景的假阳性预测。

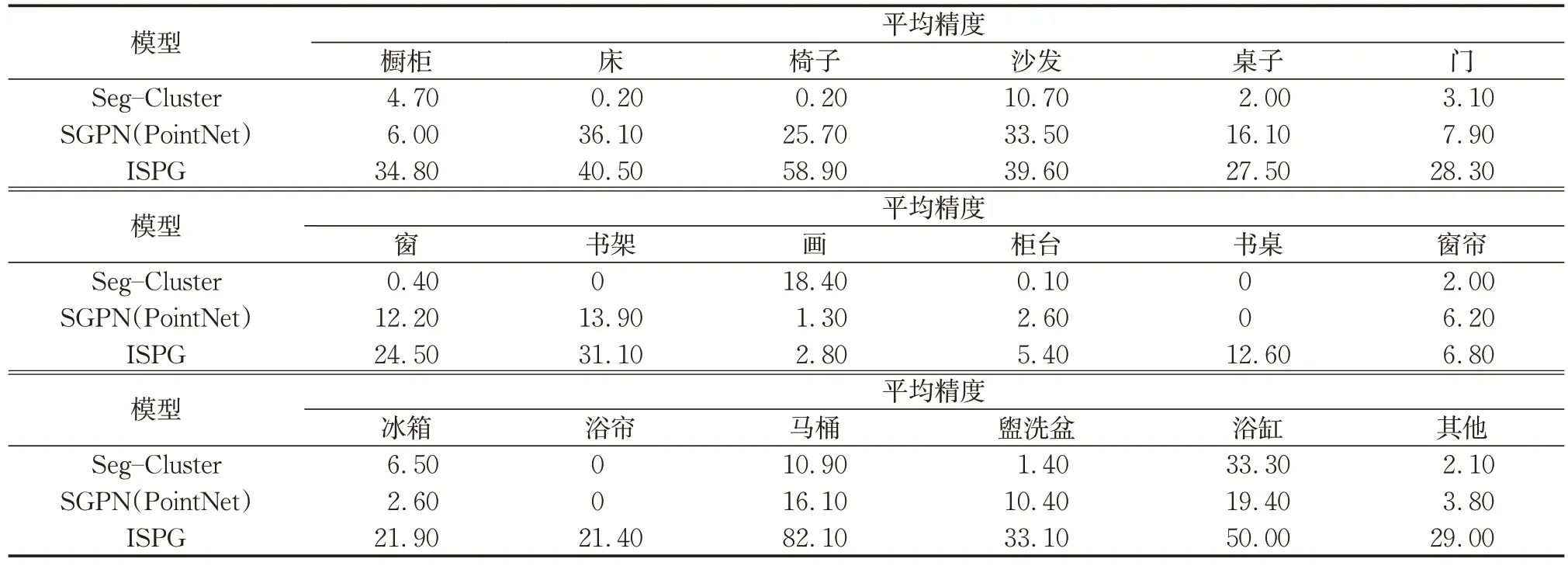
表2 ScanNet测试集IoU阈值为0.5的平均精度Tab.2 Average accuracy of ScanNet dataset with 0.5 IoU threshold

3.4 斯坦福数据集测试结果

斯坦福大型三维室内空间数据集S3DIS［1］包含从6 个区域和13 个对象扫描得到的270 个室内场景。使用203 个场景进行训练，其余67 个场景进行评估。对于斯坦福大型三维室内空间数据集（S3DIS），将每个房间分成面积为1 m×1 m的块，并且将每个点表示为九维（9D）矢量（XYZ，RGB 和归一化的空间坐标）。在训练过程中为每个模块采样了4 096个点，所有点都用于测试。

图6 ScanNet数据集上ISPG与SGPN模型可视化结果Fig.6 Visualization results of ISPG and SGPN model on ScanNet dataset

图7 显示了使用ISPG 模型在S3DIS 上的实例分割结果。由于对象实例是无序的，因此同一组中点的颜色不一定与真实情况中对应点的颜色相同。为可视化实例类，还添加了语义分割结果。ISPG模型在各种房间类型上均表现出色。ISPG 模型的测试结果与SGPN 模型相比，很少出现边缘分割混乱情况，这说明ISPG 模型的测试效果有了进一步的提升。

计算每个预测的和真实的标签之间的点的αIoU。若αIoU大于阈值，则将检测到的实例视为真阳性。进一步计算平均精度以进行实例分割性能评估，表3为IoU阈值0.5时每个类别的平均精度。

3.5 KITTI数据集测试结果

KITTI 数据集［13］包含市区、乡村和高速公路等场景，每张图像中包含丰富的行为和车辆的信息以及一些遮挡。整个数据集由389 对立体图像、光流图39.2 km视觉测距序列以及超过20万个三维标注物体的图像组成，以10 Hz的频率采样及同步。

对于该数据集，ISPG模型在小物体类别上获得了可观的收益，可以通过分区算法检测。此外，在执行空间规则化时，小物体通常与道路合并，可成为之后算法的一个改进方向。

KITTI数据集上的可视化效果如图8所示。可以看出，虽然KITTI 数据集与前两个数据集差异巨大，但是ISPG 模型依旧起到了很好的效果，说明模型具有很好的泛化能力。

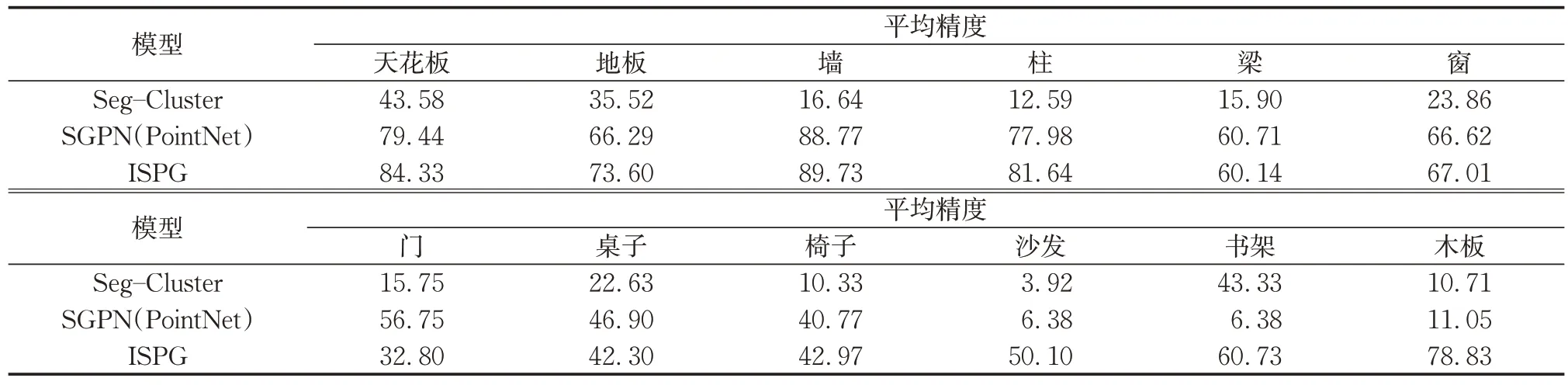
表3 S3DIS测试集IoU阈值为0.5的平均精度Tab.3 Average accuracy of S3DIS dataset with 0.5 IoU threshold

图7 S3DIS数据集上SGPN和ISPG模型可视化结果Fig.7 Visualization results of SGPN and ISPG model on S3DIS dataset

图8 KITTI数据集上ISPG模型可视化结果Fig.8 Visualization results of ISPG model on KITTI dataset

4 结语

提出了基于超点图的点云实例分割模型。首先将点云分割为超点，然后构建超点嵌入与边特征，最后通过上下文信息对超点进行分类。超点图的提出使得卷积运算不再运行在点上，而是运行在超点上，并通过丰富的边特征来表征上下文的信息，在保证分割效果的同时，加快了运行速度。在多个数据集上对该算法进行了全面的验证，取得了不错的实例分割效果。