基于IGCT的单级磁阻型线圈发射器的效率研究
2020-10-09穆泽渊黄莹倍
穆泽渊,张 军,黄莹倍
(南京理工大学 能源与动力工程学院,江苏 南京 210094)
电磁线圈发射是全电武器概念下的一种全新的发射方式,在现代军事战争中有很大应用前景。它可用于导弹发射,火箭发射,鱼雷发射和无人机弹射等[1-3]。与传统火药发射相比,其优点包括:发射消耗的能量为存储在脉冲源中的电能,较为安全且发射成本较低;发射过程中不会产生强大的冲击波,后坐力较小;发射过程中不会产生明显的火焰和烟雾,具有良好的隐蔽性;工作稳定,重复性好,不会出现传统火药发射中突然撞击和加速度突变等问题[4-5]。
磁阻型线圈发射作为电磁线圈发射方式之一,可以用于舰载导弹垂直发射技术。传统舰载导弹采用热发射方式,需要通过热管理系统排出导弹在发射仓内点火产生的高温气体,较大规模的导弹发射会使热管理系统变得庞杂[6],而磁阻型线圈发射系统可以有效地避免这个问题。与导弹冷发射方式相比,磁阻型线圈发射可以通过改变脉冲源的储能和驱动线圈的级数来适应各种型号的导弹发射时的需求,实现发射通用化[7]。
但是磁阻型线圈发射的发射机理会使导弹在发射到某个特定位置后产生一个反向的电磁力,这是导致磁阻型线圈发射效率降低的一个重要因素。本文将利用Matlab软件建立单级磁阻型电磁线圈发射器的仿真模型。在此基础上,在外电路中加入集成门极换流晶闸管(IGCT)支路来对模型进行优化,消除这部分反向电磁力,从而提高磁阻型线圈发射器的发射效率。
1 发射原理
如图1所示,磁阻型电磁线圈发射装置由铁磁性材料弹丸、驱动线圈、脉冲源以及其他部件构成。
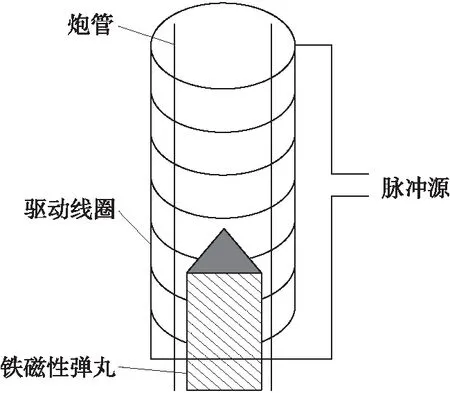
图1 磁阻型电磁线圈发射器
与感应型电磁线圈发射装置不同,磁阻型线圈发射装置的发射物不是发射线圈弹丸或者铜、铝等材料的管状弹丸[8],而是一整块铁磁性材料的弹丸。其作用机理为磁阻最小原理,在线圈-空气-铁芯磁路中,由于铁芯的磁导率远大于空气,铁芯将向磁阻最小的方向运动。当铁芯与驱动线圈两者中心重合时,磁路的磁阻最小,即弹丸发射到某个位置之后,将会收到一个与运动方向相反的电磁力,这部分反向力将导致发射效率降低。
磁阻型电磁线圈发射的物理模型主要由外电路模型和动力学模型构成。
1.1 外电路模型
如图2所示,电容器电容为C,初始电压为U0,驱动线圈的电阻为R,电感为L,二极管D1起续流作用,防止电容器反向充电,开关S1为晶闸管。

图2 外电路模型
将外电路放电过程分为2个阶段,电容器从开始放电到完全放电为第1阶段,续流支路起作用时为第2阶段。
电容器两端的电压为
(1)
式中:i(t)为放电回路中的电流。
电阻两端的电压为
UR=i(t)R
(2)
电感两端的电压为
(3)
式中:Φ为通过电感的磁通量,又Φ=L(x)i(t)。
(4)
式中:v为电枢的速度。
放电过程第1阶段的KVL方程为
UC+UR+UL=0
(5)
将式(1)~式(4)代入式(5),得:
(6)
放电过程第2阶段的KVL方程为
UR+UL=0
(7)
将式(2)~式(4)代入式(7),得:
(8)
1.2 动力学模型
驱动线圈中储存的能量:
(9)
电枢所受的电磁力:
(10)
由于舰载导弹是垂直发射,所以电枢还会受到一个垂直向下的重力mg(m为电枢的质量)。
由Ft=mv可知,电枢的动力学方程为
(11)
2 仿真分析
驱动线圈的电感与电流无关,只与线圈和铁芯的尺寸、线圈匝数、铁芯与线圈的相对位置有关[9]。通过Maxwell的静态参数化功能,可以准确地计算出驱动线圈的电感,利用Matlab的拟合分析得到近似的驱动线圈的电感函数。表1为磁阻型电磁线圈发射装置的部分参数,图3为该参数下匝数N=1时的L(x)曲线。

表1 磁阻型电磁发射装置参数
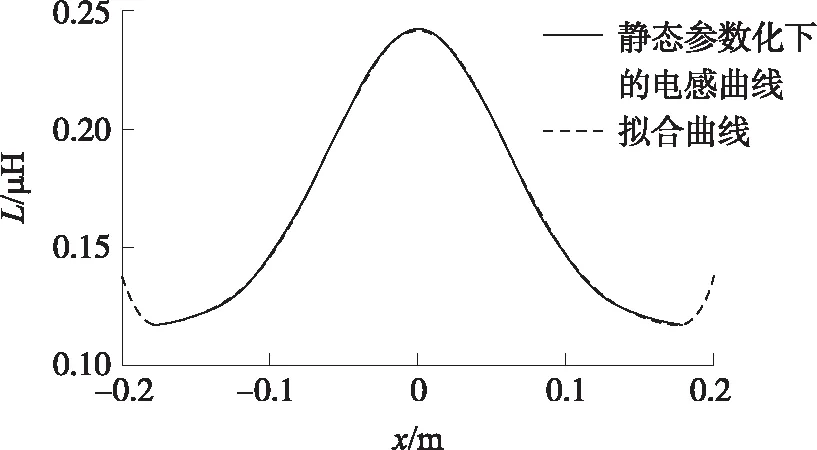
图3 Maxwell静态参数化下的电感曲线及其拟合曲线
图3中,x表示电枢运动位置,区间[-0.18,0.18]为电枢运动范围。x=0,表示电枢和驱动线圈中心重合;x<0,表示电枢在驱动线圈下方;x>0表示电枢在驱动线圈上方。如图3所示,拟合后的电感函数曲线与Maxwell精确计算出的驱动线圈的电感曲线差异很小,这表明拟合后的驱动线圈的电感函数可以准确地描述驱动线圈在电枢运动区间内的电感。
2.1 单级磁阻型线圈发射仿真模型
得到驱动线圈的电感函数L(x)后,按照外电路放电过程,采用Matlab建立了磁阻型电磁线圈发射装置的两段仿真模型。
如图4所示,图4(a)为磁阻型电磁发射装置电容器完全放电的外电路仿真模型,描述图2中电容器初始电压U0变为0时的外电路的放电过程;图4(b)为该阶段的总仿真模型,描述电容型脉冲源完全放电阶段电磁发射器的发射过程。图中,v1,i1,x1分别表示第1阶段仿真结束时电枢的速度、回路电流和电枢位置。
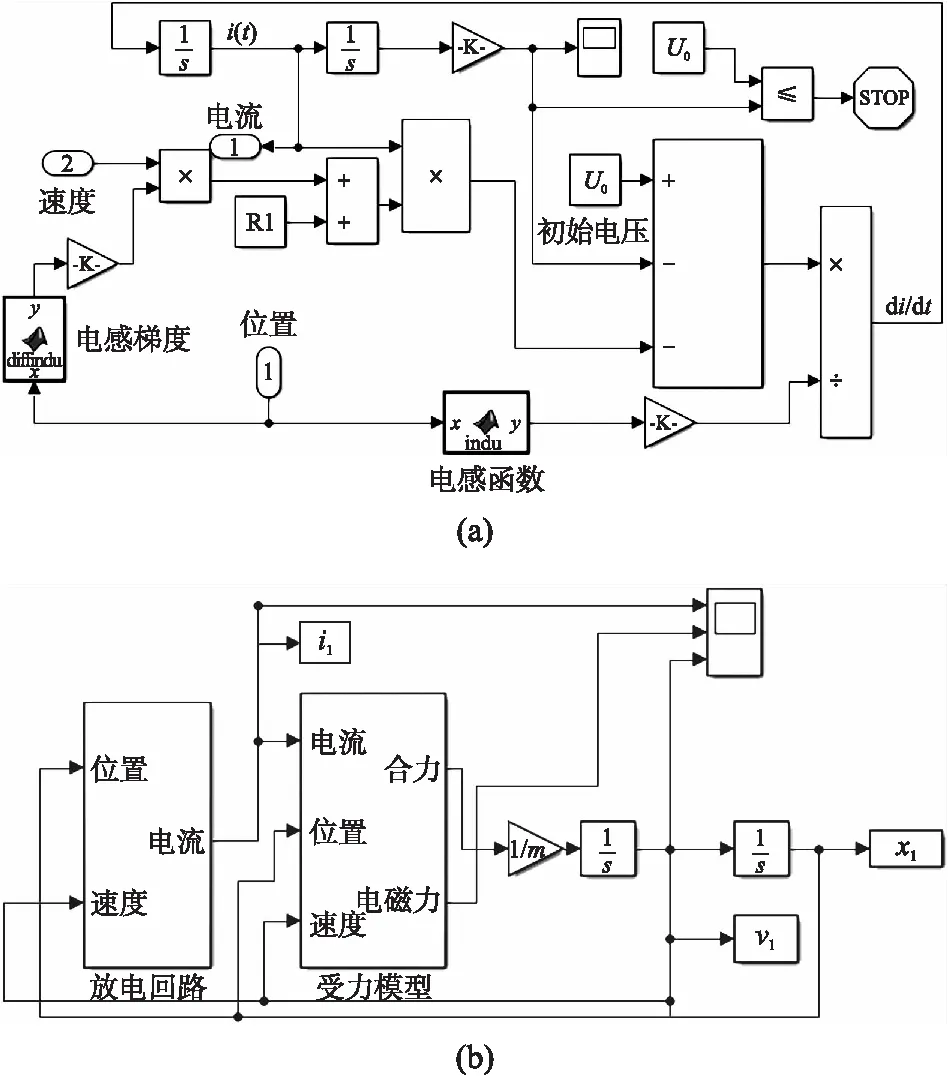
图4 磁阻型电磁发射装置放电过程第1阶段的仿真模型
如图5所示,图5(a)为磁阻型电磁发射装置放电过程第2阶段的仿真模型,描述图2中驱动线圈与二极管D1、晶闸管S1组成续流回路时的外电路放电过程。图5(b)为该阶段的总仿真模型,描述该阶段电磁发射器的发射过程。图中,i2为第2阶段仿真的回路电流。
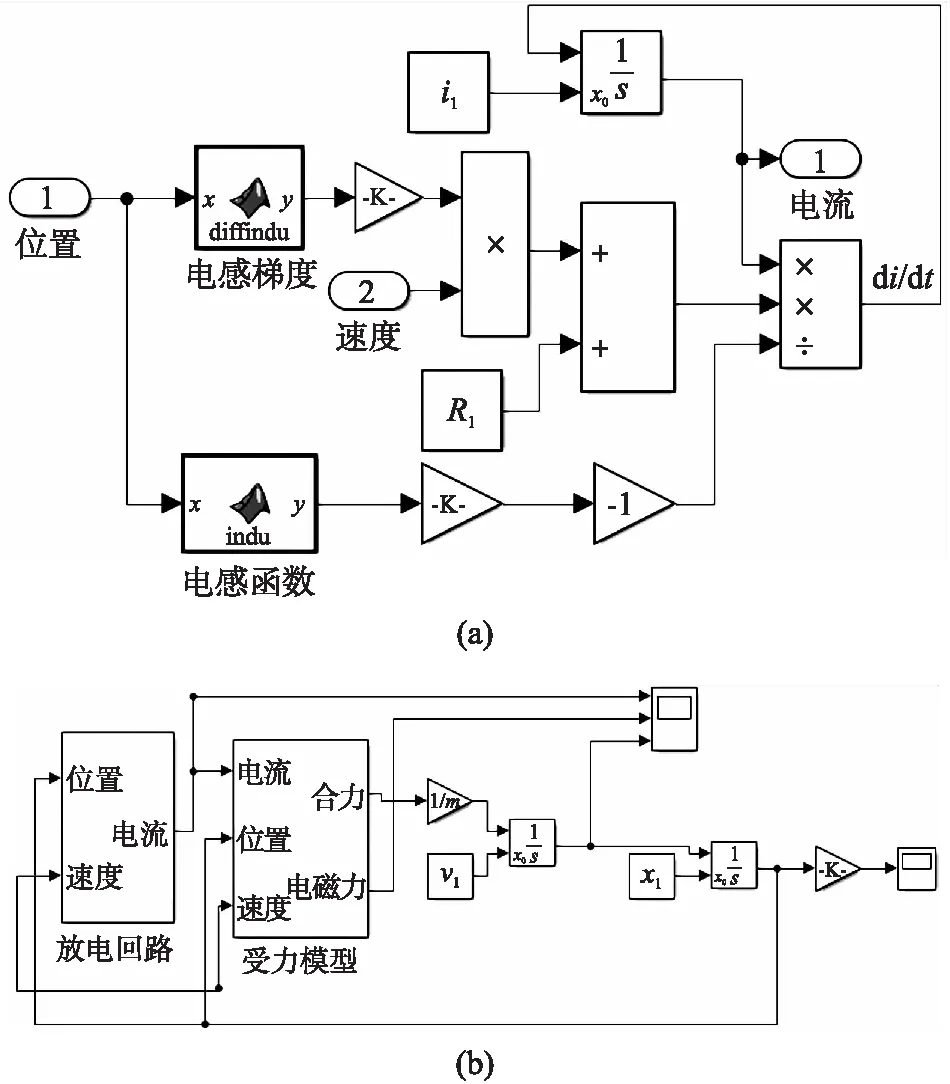
图5 磁阻型电磁发射装置放电过程第2阶段的仿真模型
电容的初始电压U0=2 500 V,电容C=4 mF,驱动线圈电阻值R=0.1 Ω,匝数N=80,电枢质量m=50 kg,初始位置x0=-0.07 m,在此参数下,对磁阻型线圈发射装置进行了仿真实验,仿真结果如图6所示。
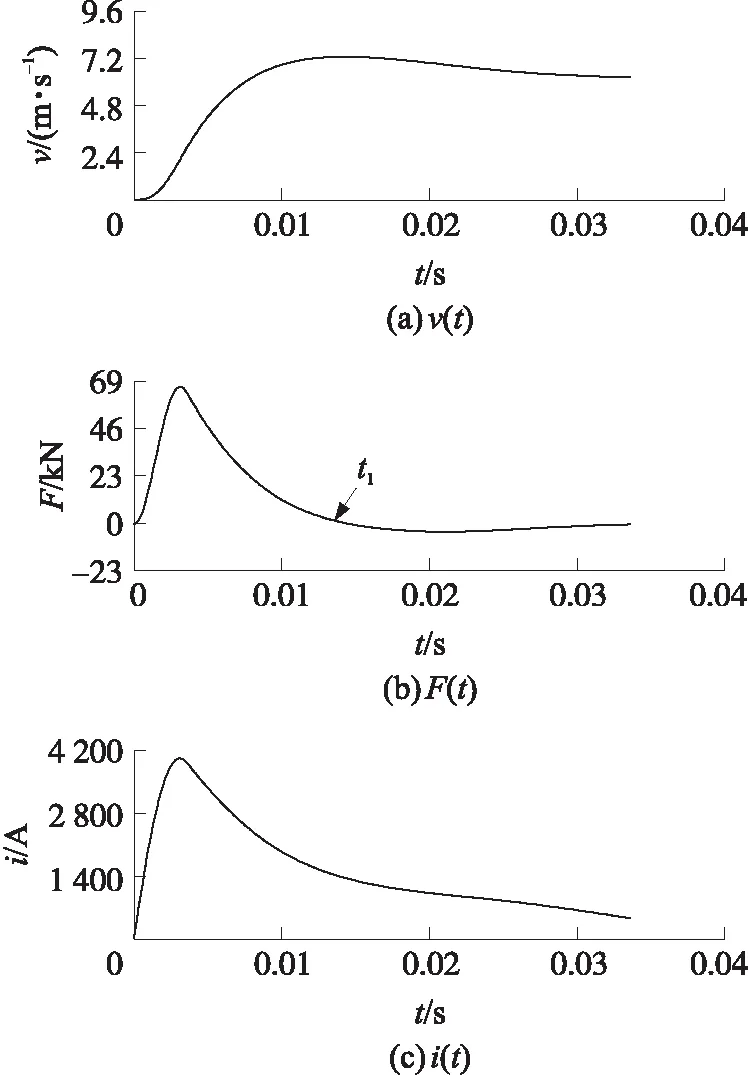
图6 磁阻型电磁发射装置的v(t),F(t),i(t)曲线

2.2 优化后的单级磁阻型线圈发射仿真模型
图7为发射装置未进行优化时电枢处于不同运动位置所受的电磁力曲线。
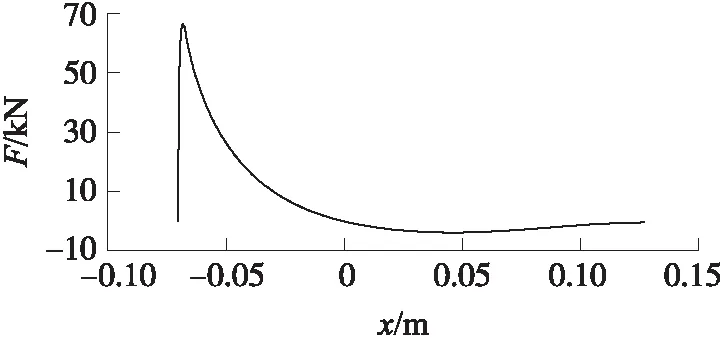
图7 未优化时发射器的电枢不同运动位置点所受的电磁力曲线
如图7所示,当电枢位置由x<0变为x>0时,电枢所受电磁力由正向变为反向。由式(10)可知,可以通过减小此时驱动线圈的电流来减小电枢运动过程中的这部分反向电磁力。在电感型脉冲源技术中,可通过半导体断路开关来实现对某一回路电流的切断。在半导体型断路开关中,IGCT单管容量大,应用成熟,因此本文将外电路中的半控型器件晶闸管替换为全控型器件IGCT。当位置传感器识别到电枢中心与驱动线圈中心重合时,IGCT的门极驱动电路控制其关断,使驱动线圈的电流迅速降低,从而消除这部分反向电磁力。如图8所示,可用Switch模块组实现这一过程。
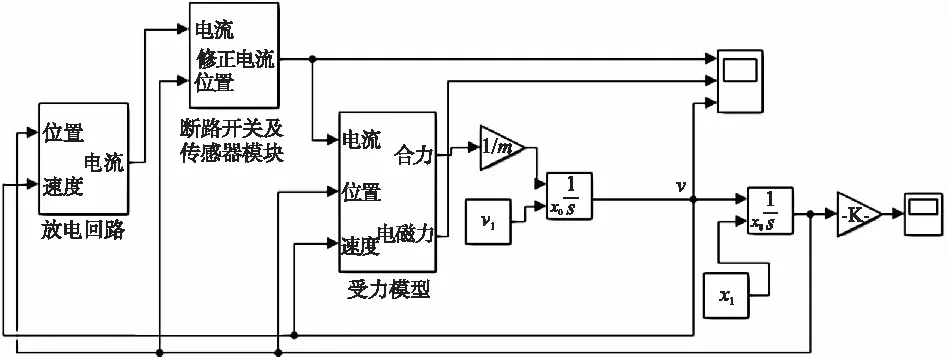
图8 优化后的电磁发射装置第2阶段总仿真模型
由于电容器完全放电时间很短,以及电枢速度较低,当电容器完全放电完成时,电枢远远未运动到驱动线圈中心点,即电磁力还未改变方向,优化后的第1阶段仿真模型与优化前一致。
磁阻型线圈发射装置的参数不变,对该装置进行仿真实验,仿真结果如图9所示。
图9(a)、9(b)和9(c)分别为磁阻型线圈发射装置优化后的电枢速度曲线v(t),电枢所受电磁力曲线F(t)和放电电流曲线i(t)。t1时刻之后,门极驱动电路控制IGCT完成关断,驱动线圈的电流迅速降为0;图9(b)中电枢所受电磁力变为0;图9(a)中电枢的速度曲线相比图6中下降趋势明显放缓,出口速度为7.07 m/s;发射效率η=10.0%。相比未优化前,发射效率得到了提升。

图9 改进后发射装置的v(t),F(t),i(t)曲线
2.3 初始位置对模型改进前后发射效率的影响
其他参数条件不变时,研究初始位置对模型改进前后的发射效率的影响,结果如图10所示。
图10为电磁发射装置未进行优化时初始位置为-0.11 m,-0.10 m,-0.09 m,-0.08 m,-0.07 m,-0.06 m时的电枢速度曲线,其中初始位置从-0.11 m变化到时-0.06 m,出口速度先变大后变小,这表明存在一个最佳的初始位置。可以看到当x0=-0.09 m时,出口速度达到最大,为6.79 m/s,则模型未优化时最大发射效率为9.22%。
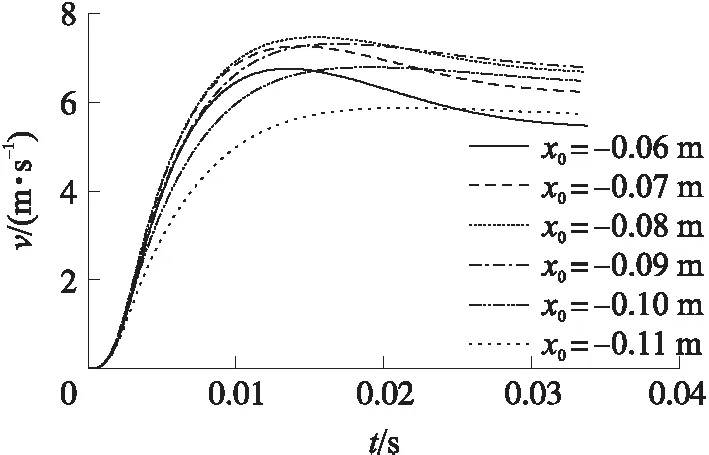
图10 未优化时不同初始位置下的电枢速度曲线
图11为电磁发射装置优化后初始位置为-0.11 m,-0.10 m,-0.09 m,-0.08 m,-0.07 m,-0.06 m时的电枢速度曲线,其中初始位置从-0.11 m变化到-0.06 m时,出口速度同样先变大后变小。可以看到,模型优化后x0=-0.08 m时出口速度达到最大,为7.28 m/s,则模型优化后的最大发射效率为10.6%。

图11 优化后不同初始位置时的电枢速度曲线
由上可知,模型改进后提高了发射效率的最大值,且由于消除了反向的电磁力,最佳初始位置点在发射管道内将会前移,这样可以使电枢在加速区获得更好的加速效果。
2.4 电枢初速度对最佳初始位置的影响
其他参数条件不变,电枢初速度分别取0 m/s,2 m/s,4 m/s,6 m/s时,研究改变初始位置对改进后仿真模型发射效率的影响,仿真结果如图12所示。
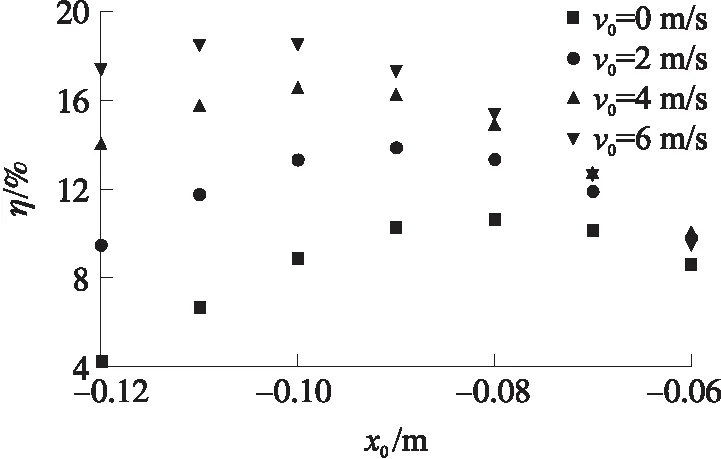
图12 电枢不同初速时不同初始位置的发射效率
由图12可知,电枢初速度不同时,最佳初始位置也会不同。电枢初速度增加时,最佳初始位置不断向左偏移,即电枢最佳初始位置在发射管道中不断后移。这表明对于多级磁阻型电磁线圈发射系统,为了增加发射效率,每级发射系统的初始距离应随着级数的增加而增大,电枢初速度每增加2 m/s,发射系统的初始距离需相应增加0.01 m。
3 结论
本文通过Matlab和Maxwell建立了单级磁阻型电磁发射装置的仿真模型,在此基础上,在外电路中加入了断路开关IGCT支路,对其模型进行了优化,消除了电枢运动过程中受到的反向电磁力。仿真分析结果表明:模型优化可以大大提高磁阻型电磁发射装置的发射效率,且最佳初始位置将会前移,而电枢初速度的增加会使最佳初始位置后移。本文研究结果为多级磁阻型电磁发射装置的设计和优化提供了基础。
