低速陶瓷球侵彻明胶研究

张志倩,赵太勇,印立魁,付建平,于寅业,张佳玉

(1.中北大学 机电工程学院 山西 太原 030051;2.中北大学 地下目标毁伤技术国防重点实验室,山西 太原 030051;3.晋西工业集团有限责任公司,山西 太原 030051)

在现代战争中,随着战斗部技术的快速发展,以高性能、低成本的陶瓷球等为代表的新型战斗部毁伤元应运而生。与普通钨合金、钢质破片相比,陶瓷球具有强度高、比动能大、价格低廉、容易生产等优点,可对近距离有生力量进行有效打击。创伤弹道学研究,常采用明胶作为人体组织的替代物,因此研究低速陶瓷球侵彻明胶对人体杀伤机理具有重要意义[1-2]。近年来,国内外学者对球形破片侵彻明胶的运动进行了大量的试验与理论研究,其中莫根林等[3-4]根据球形破片侵彻明胶的空腔实验数据,推导出空腔的运动为正弦运动;刘坤等[5]引入明胶抗力进一步完善了球形破片侵彻明胶的修正力学模型;文献[6]通过无网格数值方法(SPH方法)研究弹丸在人体组织替代物中的渗透;文献[7]研究了在较低的冲击速度(120 m/s)下明胶材料对球形钢弹丸穿透的响应;文献[8]通过实验和计算方法研究了中等速度下钢球在明胶中的侵彻,通过理论计算出的明胶一个点的压力、瞬时空腔尺寸时间历程与相应的实验测量的时间历程吻合得很好;金永喜等[9]利用相似理论推导出明胶瞬时空腔效应的相似准则方程,从而建立了明胶靶标与肌肉目标的空腔效应等效模型。

目前,对陶瓷材料作为毁伤元的毁伤机理和明胶侵彻响应特性有了初步认识,但针对陶瓷球低速侵彻明胶的研究相对较少,进行低速陶瓷球对明胶的毁伤效应研究是武器系统效能评估的重要内容,且低速陶瓷球具有低附带毁伤特性,具有重要军事意义。故需要开展低速陶瓷球侵彻明胶的研究。本文通过弹道冲击试验,基于数值模拟和能量守恒理论计算研究了不同直径和不同冲击速度下陶瓷球侵彻明胶的规律。

1 理论分析

图1 理论分析模型

陶瓷球侵彻明胶是动态过程,明胶包含变形能和动能,明胶的破坏可分为破碎区和弹性区。假设陶瓷球释放的动能全部转化为明胶径向运动的动能和明胶的变形能,利用能量守恒原理,对陶瓷球侵彻明胶进行分析。根据文献[10]中的模型,明胶与陶瓷球的分离点在靠近头部顶点的位置,随着侵彻速度降低,分离点逐渐向后移动,直到低到临界速度(vc=10 m/s±2 m/s)及以下,分离点保持在与侵彻方向垂直的最大横截面处。如图1所示,在柱坐标系(z,r)中,rk为明胶形成的空腔半径,rj为弹性区和破裂区交界位置的半径,rb为明胶的边界尺寸,v0为弹丸冲击速度,rq为陶瓷球半径。

在弹道某一位置处,取轴向厚度dz的一层明胶为研究对象,该层明胶的动能为[11]

(1)

在研究陶瓷球侵彻明胶时的变形能时,假设明胶中球形空腔以很低的速度膨胀,因此空腔周围有破裂变形区和弹性变形区,动量守恒和质量守恒方程为

(2)

(r-u)2d(r-u)=r2dr

(3)

式中:u为径向位移,σr为径向应力,σθ为拉伸应力。

对于破裂区,由边界条件r=rk,破裂区σθ=0,求解可得:

(4)

(5)

(6)

式中:c1和c2为模量,p为明胶内各向压力。

当空腔r=rk时,结合动量守恒式(2),则rk处空腔径向应力为

(7)

由式(4)可得:

(8)

假设边界条件σr(r=rb)≈0,同理得出:

(9)

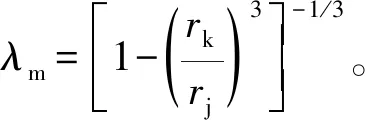
对于破裂变形能,由于σθ=0,联立式(7)、式(8)可得微元层破裂变形能dEc:

(10)

将边界条件rb≈∞代入,则可简化式(9):

(11)

对于弹性区,微元层弹性变形能dEe为

(12)

由能量守恒,有

dEk,p=dEk,g+dEc+dEe

(13)

式中:dEk,p为微元层陶瓷球动能,dEk,g为微元层明胶动能,dEc为明胶微元层破裂变形能。化简式(13)，整理可得侵彻深度h:

(14)

式中:mp为陶瓷球质量,v0为陶瓷球冲击速度,λm取值为1.5～2.0。利用Matlab软件求解超线性方程,可解出侵彻深度h。

2 试验方法

试验在室内靶道进行。采用7.62 mm口径滑膛枪发射,用弹托支撑不同直径的陶瓷球分别侵彻500 mm×500 mm×300 mm明胶,由测速仪器测量出陶瓷球速度,如图2所示。

图2 试验原理及实验场地

明胶靶制作过程:明胶颗粒与水的质量配比为1∶5,采用温度为60 ℃水浴加热的方式,将明胶颗粒溶于水形成明胶溶液,并在4 ℃的环境下凝固,制成的明胶靶如图3所示。图4为d=2 mm,3 mm,5 mm的陶瓷球。

图3 明胶

图4 陶瓷球

3 数值模拟方法

图5 有限元网格模型

表1 模型材料参数

4 试验结果及分析

4.1 陶瓷球侵彻明胶理论与试验的对比

利用d=2 mm,3 mm,5 mm的陶瓷球进行侵彻明胶试验,结果发现陶瓷球的直径越大、冲击速度越高,其在明胶中的侵彻深度越深,试验结果相关参数如表2所示,表中,d为陶瓷球直径,v0为冲击速度,h为侵彻深度。图6为不同直径的陶瓷球侵彻试验结果。

表2 试验结果

图6 不同直径不同速度侵彻明胶试验结果

将理论计算结果、试验结果与数值模拟进行对比,发现三者趋势相同,如图7所示。文献[6]和文献[8]试验数据为高速球形破片,将其与理论模型值进行对比,如图8、图9所示,发现理论侵彻深度与试验结果误差在10%以内,说明理论模型可适用低、中、高速度,因而具有一定的参考价值。

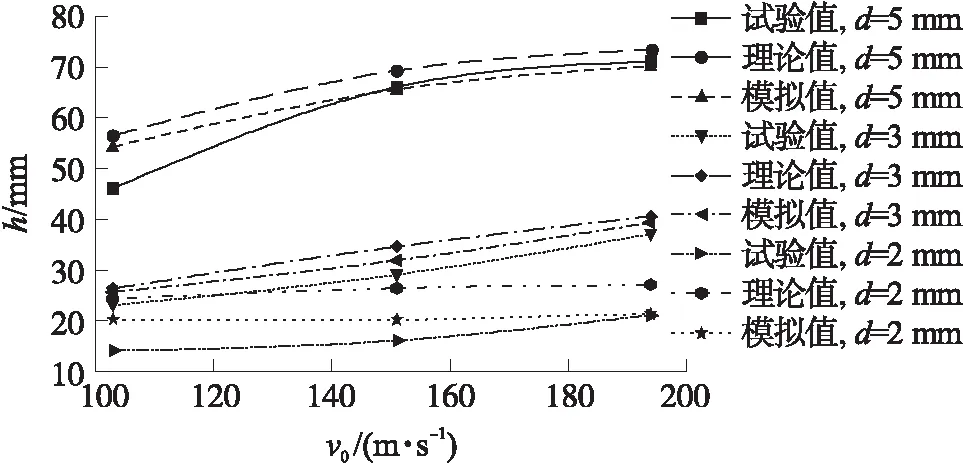
图7 理论模型、实验值、数值模拟的对比

图8 理论模型与文献[6]数据的对比

图9 理论模型与文献[8]数据的对比

4.2 陶瓷球直径和冲击速度对侵彻明胶的影响

通过数值模拟的方法,改变陶瓷球的直径和冲击速度,如图10所示。在0.16 ms时,试验结果与数值模拟结果中明胶的破坏形态基本吻合,说明本文选取的数值模拟材料参数具有一定的可靠性。明胶的侵彻深度和形成的空腔是评价创伤弹道的重要的杀伤参数,因此,需要进一步研究冲击速度v0和陶瓷球直径对侵彻深度h、最大瞬时空腔的影响。图11为根据试验数据绘制的陶瓷球直径和冲击速度v0对侵彻深度h的影响结果。研究发现:陶瓷球的直径越大、冲击速度越高,侵彻深度则越深;且陶瓷球直径的改变比冲击速度的改变对侵彻深度的影响更大。因此,低速下陶瓷球的直径是决定侵彻深度的主要因素。最大空腔直径随陶瓷球的直径和冲击速度的增加而增加,陶瓷球直径、冲击速度对最大空腔直径dk,m的影响如图12所示。由图可见,陶瓷球的直径和冲击速度同时影响最大空腔直径。

图10 不同陶瓷球直径、不同速度侵彻明胶的数值模拟结果

图11 冲击速度和陶瓷球直径对侵彻深度的影响

图12 冲击速度和陶瓷球直径对最大空腔直径的影响

4.3 不同材料的球形破片对侵彻明胶的影响

为研究不同材料的球形破片对侵彻明胶的影响,将陶瓷球、钢球、钨球侵彻明胶进行对比。利用数值模拟方法研究直径d=3 mm的不同材料的球形破片侵彻明胶时的速度v的衰减情况,发现3种材料在初始冲击速度v0=103 m/s,151 m/s,194 m/s情况下,陶瓷球的速度衰减最快,钢球和钨球速度衰减较缓,结果如图13所示。

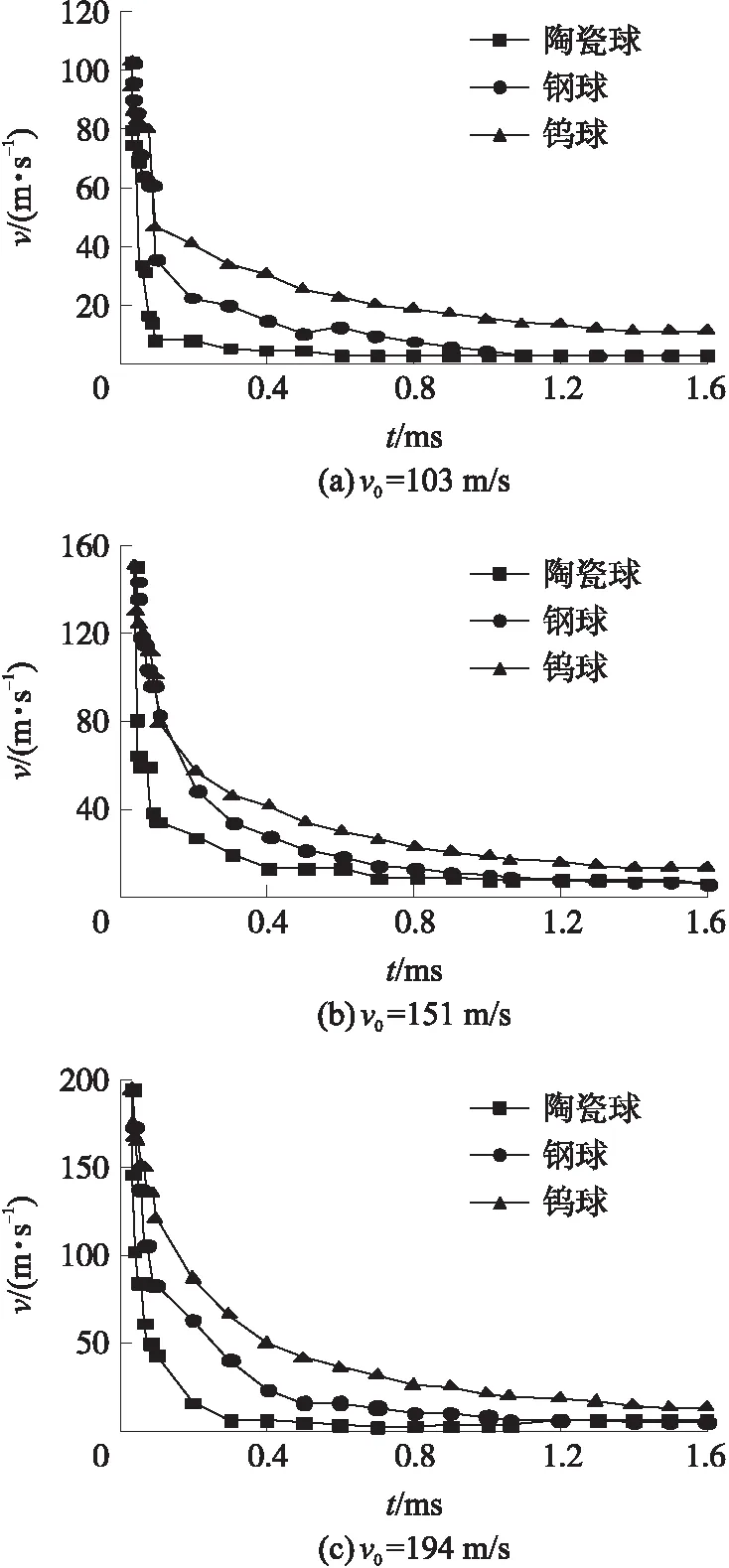
图13 不同材料球形破片侵彻明胶的速度随时间的衰减

在研究破片的材料对侵彻深度和最大空腔半径的影响时,冲击速度v0分别取103 m/s,151 m/s,194 m/s。由于侵彻深度h与最大空腔半径rk,m是评价毁伤的重要参数,将二者之和H作为综合毁伤参数,H与破片初始动能Ek0的关系如图14所示。根据图14,陶瓷球、钨球和钢球对应的侵彻深度与最大空腔半径之和H的差异较小。分析其原因:在保证初始动能相同的情况下,随着密度的增加,破片的半径减小;而结合式(14)可知,侵彻深度h与最大空腔半径rk,m反相关。因此,明胶的空腔越大,对应的侵彻深度越小。3种材料的侵彻深度与最大空腔半径之和H的差异较小,而陶瓷球具有强度高、比动能大、价格低廉、生产容易等优点,更适合作为毁伤元。

图14 初始动能对综合毁伤的影响

4.4 永久空腔的形成

在试验中发现有永久空腔的现象,见图15。

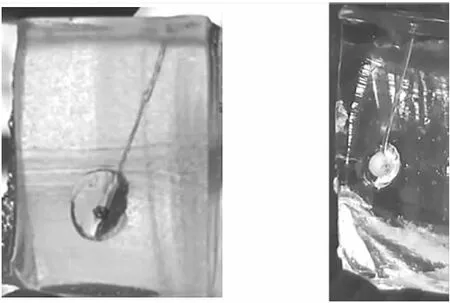
图15 永久空腔

陶瓷球侵彻明胶产生压力,开始只有直接作用的质点离开冲击平衡位置,力的作用和反作用使相邻质点离开冲击平衡位置而运动起来,明胶内的扰动在介质中逐渐由近及远传播出去而形成应力波。但由于明胶制作工艺中可能存在搅拌不均匀,凝固时明胶的密度不均匀,导致明胶力学特性各异。因此应力波在传播、反射和相互作用过程中产生差异,明胶产生永久空腔的现象。人体中各种组织密度、结构也存在着不同,也可能产生永久空腔,而永久空腔对人体杀伤有重要影响。

5 结论

本研究通过理论分析、试验验证和数值模拟3种方法,对低速陶瓷球侵彻明胶进行研究,得到以下结论:

①本文理论分析模型计算出的陶瓷球侵彻明胶深度与试验结果有较好的一致性;理论模型具有可靠性,此理论模型可为计算球形破片侵彻明胶的深度提供参考。

②利用试验和数值模拟的方法改变陶瓷球的直径和冲击速度,发现在低速下直径是影响陶瓷球侵彻明胶深度的主要因素。

③利用数值模拟方法对钨球、钢球、陶瓷球在相同初始动能和冲击速度下侵彻明胶的情况进行对比,发现三者侵彻深度与最大空腔半径之和差异较小,考虑到侵彻材料自身特点和经济性,陶瓷球更适合作为毁伤元。