大口径平顶弹体击水动力学方程研究
2020-10-09吴茂林戴文留孙玉松陆泽平
汪 振,吴茂林,戴文留,孙玉松,陆泽平
(1.海军工程大学 兵器工程学院,湖北 武汉 430033;2.海军装备部驻上海地区第一军事代表室,上海 201913;3.江南工业集团有限公司,湖南 湘潭 411207)
入水冲击问题[1-3]广泛存在于海上各种兵器的作战使用过程中,包括空投鱼雷入水、深水炸弹入水、水下无人航行器(UUV)布放、反潜导弹入水、炮弹入水等。
弹体入水冲击载荷与入水速度大小和弹体姿态有着密切的关系。传统的航空深弹、空投鱼雷等武器的入水速度均在较低水平,入水冲击载荷的瞬时峰值不大。随着技术的发展,未来深弹入水速度将很容易达到200 m/s以上。在高速入水初期的几毫秒瞬间,弹体会受到巨大的冲击载荷,入水时的冲击载荷可能会造成弹体结构损伤,内部电子器件失灵,入水弹道失稳、忽扑、跳弹等不良后果。
为了增加杀伤效果,需要增加战斗部装药量,所以弹体的质量较大;同时为了防止深弹小角度入水跳弹问题,弹体通常采用平顶弹头设计;这种大口径、大质量的平顶弹头弹体高速入水时将受到高幅值的瞬时冲击载荷。目前,针对这种大口径、大质量的平头弹体高速入水问题的研究较少。
目前有众多学者针对该问题采用试验、理论和数值模拟的方法进行了研究。陈诚等[4]对超空泡航行器20°角倾斜入水冲击载荷特性进行了试验研究。理论研究自冯卡门[5]提出的附加质量的楔形体入水模型开始,魏卓慧等[6]采用附加质量法建立了截锥形弹体垂直入水冲击载荷的理论计算模型。随着计算机技术以及有限元方法的发展,另有学者采用数值模拟的方法研究该问题。孙琦等[7]基于LS-DYNA软件运用ALE方法对弹体撞水过程进行了分析。
由于弹体高速入水物理过程极其复杂,要从理论上建立一个完全相同的模型较为复杂。本文对弹体入水过程进行一定简化,根据流体动量定理对具有平顶头型的大口径弹体入水冲击动力学方程组进行了理论推导。
1 稳定流体的动量、动量矩定理
根据流体力学[8],假设稳定流动流体的某一质点系中一质点的质量为dm1,它的运动速度为v1,则质点系的动量为
(1)
若此质点到空间中一定点O1的矢径为rO1,则此质点的动量对定点O1的矩为
(2)
质点系的动量对时间的变化率等于质点系所受外力矢量和,即
(3)
质点系对O1点的动量矩对时间的变化率等于质点系所受外力对于O1点力矩的矢量和,即
(4)
设流体中某一质点系的控制面积为S1,流体控制域为Ω,那么该控制面上所受到的外力矢量和为
(5)
式中:vn为垂直于控制面的速度大小。
从方程(5)中可以看出外力矢量和F由两项组成:前一项为单位时间内通过控制面的流体动量代数和;后一项为控制体内流体动量对时间的变化率,当控制体固定并且是定常流动时,该项为0。后者反映了流体运动的非定常性,是由控制体内流体动量随时间变化而产生的一种力。
本文不考虑弹体击水时流体的非定常性,即不考虑方程(5)中的第二项,仅考虑通过控制面的流体动量代数和。则该控制面上的外力对于某一定点O1的力矩矢量和为
(6)
2 大口径弹体击水过程力与力矩方程
2.1 条件假设
对于大口径弹体击水问题,对其初始条件以及相关因素做如下假设:
①水面平静无涌浪,即水面为平面;
②弹体击水瞬间,弹体速度方向与弹轴重合,即无攻角;
③击水过程中,弹体无绕弹轴自转,即无横滚;
④弹体击水瞬间,水同时撞击弹体表面,即水与深弹的接触面为控制面;
⑤在击水过程极短时间内,接触面上无空泡现象;
⑥不考虑水的压缩性与弹体的弹性;
⑦不考虑水的黏性。
2.2 直角坐标系中动力学方程
弹体直角坐标系:设置直角坐标系原点O与弹体质心重合;x轴与弹轴重合,指向弹头方向;y轴与x轴垂直,指向弹体上方;z轴由笛卡尔坐标系右手法则获取。
由牛顿第三定律,弹体对水的撞击力与水对弹体的撞击力大小相等、方向相反。为了方便分析,将水以速度v对弹体表面上趋于某一点P的微元面积ΔS上的撞击力FP投影在xOy和yOz平面上。
假设弹体头部P点的切平面与弹体的夹角为α;则过P点的切平面与xOy平面的交线夹角也为α;假设β为FP在yOz平面上的投影与y轴的夹角,由于FP指向弹轴,所以该投影通过x轴。如图1所示。

图1 直角坐标投影图
根据上述坐标系以及假设参量,则由方程(5)得到水对深弹表面P点微元面上的法向撞击力FP大小的标量方程:
ΔFP=ρv2(sin2α)ΔS
(7)
则撞击力ΔFP在x,y,z轴上的投影分别为
(8)
对式(8)进行积分,则有:
(9)
同理,根据方程(6)可求出对x,y,z轴的矩Mx,My,Mz。因为
(10)
式中:rP为P点到x轴的距离,即P点所在截面圆的半径;xP为P点x方向坐标,即P点所在截面圆距质心O的距离。因为速度v与P点的微元面成α角,所以FP的作用点在距P点距离为e的Q点上。
(11)
rQ=rP-esinα
(12)
xQ=xP+ecosα
(13)
因为ΔS→0,所以e→0;
所以,rP≥esinα,xP≥ecosα。
因此,rP≈rQ,xP≈xQ。
根据方程(6),有下列方程:
(14)
式中:r表示弹体头部母线方程,即
r=f(x)
(15)
2.3 坐标变换
由于弹体是回转体,所以采用柱面坐标系(x,r,β)来简化求解Fx,Fy,Fz,Mx,My,Mz的过程。建立柱面坐标系:设柱面坐标系的原点与弹体质心重合;x轴与弹轴重合,指向弹头方向;r轴与x轴垂直,指向回转半径方向;β角以直角坐标系y轴反向为基准,在原直角坐标系yOz平面上,按照逆时针旋转为正。
积分微元变换:因为弹体头部母线方程为r=f(x),设r′=dr/dx,则
(16)
由于弹体头部任意一点与水相切时夹角为α;根据建立的柱坐标系以及几何关系,则有:tanα=dr/dx=r′,如图2所示。

图2 弹体切线图
则推导出:
(17)
2.4 积分域的确定
因为r=f(x),所以弹体头部母线在直角坐标系xOy平面上的方程为

(18)
在不考虑弹体击水的瞬间水面隆起的情况下,假设水面为一条直线,弹体击水的过程即水面方程相对弹体向上运动的过程,如图3所示。图中,d为弹体顶点到质心即坐标原点O的距离;a为弹体头部椎体与弹体圆柱部后段交面所在x轴上的坐标,即锥头与圆柱交面到质心的距离。

图3 弹体水面相交图
该过程水面方程在直角坐标系xOy平面上的表达式为
y=(x-xC)tan(θ-δ)
(19)
式中:θ为弹体击水过程中任一瞬间速度矢量与水平面的夹角;δ为任一瞬间弹轴线与速度矢量的夹角,即攻角;φ=θ-δ,为任一瞬间弹轴与水平面的夹角。
xC为弹轴与水面交点到弹体质心(O点)的距离(坐标),有

(20)
当t=0时,xC0=xC1,表示弹体第一点与水面接触时弹轴与水面的交点到弹体质心O点的距离。
由图3可知,变量x的积分区间可按照下列步骤求得。
联立弹体头部母线方程与水面方程(18)第2式、方程(19),即
(21)
解得x1;再联立方程(18)第1式、方程(19),即
(22)
解得x2。
则积分区间分别为:x1≤x≤x2和x2≤x≤d。
对于变量β的积分区间,因为弹体是回转体,考虑其中心对称性,所以弹体关于入水时xOy平面对称。在任一截面上β总是与y轴对称,分别为-β和β,如图3所示。所以,当x1≤x≤x2时,根据几何关系可知:
(23)
同时,可以推导出:
(24)
当x2≤x≤d时,弹体头部完全浸没在水中,此部分弹头任意x处截面的表面圆周均沾水。此时,则有β1=-π,β2=π。
2.5 弹体击水力和力矩方程
将dS,sinα,cosα,sinβ,cosβ对应表达式(16)、式(17)、式(24),代入Fx,Fy,Fz,Mx,My,Mz方程组(9)、方程组(14)中,经过严格的数学推导以及坐标变换,得到弹体击水力和力矩方程,具体数学推演过程如下。
①Fx。
(25)
当x2≤x≤d时,式(25)为

当x1≤x≤x2时,式(25)为

②Fy。

(26)
当x2≤x≤d时,式(26)为
当x1≤x≤x2时,式(26)为

③Fz。

④My。

⑤Mz。

(27)
当x1≤x≤x2时,式(27)为
当x2≤x≤d时,式(27)为
综上数学推导过程,则有
(28)
式中:

3 平顶弹体击水力与力矩
对于部分弹体,为解决小着角的跳弹问题,均采用平顶结构设计。目前正在设计的部分悬浮式弹体,为增加战斗部装药,弹体结构通常也需要采用平头结构。
对于这种结构,平顶部分的击水力以及力矩方程可采用分区间积分的方式。对于具有母线方程的部分仍采用前文所推导的公式,对于平顶部分仍然根据式(11)~式(13)、式(20)~式(22)进行推导。
设弹体平顶平面半径为R0,在平顶平面上,平面击水时α=90°。此时水面与平顶圆周的交点与平顶圆心的连线与y轴负方向的夹角为Φ,根据平顶击水时与水面相交的几何关系,则有
(29)
根据以上假设以及数学推导,得到平顶平面击水时弹体受力公式:
(30)

结合弹头平顶平面击水公式以及弹头母线部分击水公式,得到平头弹体击水力和力矩方程:
(31)
4 弹体击水过程运动方程
在弹体击水过程中,大部分表面与空气接触,仍然存在着空气动力和空气动力矩,但是远小于击水时力与力矩。在建立入水瞬间弹体的运动方程时,仅考虑弹体自重以及击水时的力与力矩。由前文所述力学方程可知,在弹体击水过程中只需要在二维坐标系上建立其运动方程[9]。建立大地坐标系与弹体坐标系中弹体运动示意图,如图4所示。

图4 弹体运动示意图
则其运动学方程组为
(32)
式中:Fx,Fy分别为弹体所受轴向力和径向力;Mz为弹体所受力矩;m为弹体质量;Iz为弹体的赤道转动惯量;g为重力加速度;φ为弹轴倾角;δ为攻角;θ为弹道倾角;X为弹体在平面内水平位移;Y为弹体在平面内竖直位移;v为任一时刻速度大小。
初始条件:速度v0,弹道倾角θ0,攻角δ=0,弹轴倾角φ0。
5 弹体击水三自由度方程组
结合平顶弹体运动学及动力学方程组,在不考虑侧偏、侧摆以及横滚3个自由度的情况下,假设母线方程为圆弧的弹体,建立平顶弹体击水三自由度方程组,计算弹体击水瞬间各个参数。平顶弹体击水三自由度方程组为
(33)
(34)
式中:A,B,D,E,G,H同前文。
已知数据如下。头部曲面与圆柱面交线的x坐标:a;平顶平面x坐标:d;弹体圆柱段半径:R2;弹体质量:m;弹头曲面母线半径:R3;弹体赤道转动惯量:Iz;海水密度:ρ;弹轴倾角:φ0;弹体初始速度:v0;弹头平顶面半径:R0;弹头母线方程式:r。
弹体表面第一点触水零时刻,弹轴与水面方程交点x坐标:xC0=d+R0tanφ。
根据几何关系,则有
(35)
(36)
6 计算过程分析
弹体入水过程如图5所示。

图5 弹体入水过程
对弹体击水分阶段进行积分,根据图5几何关系,计算各阶段水面与轴线交点坐标:
(37)
①当水平面与弹轴交点C在图5中C1到C2区间时,水平面与xOy平面的上下母线交点由方程组确定:
(38)
其中必有一解xa在a与d之间,所以取x1=xa;由于水平面与上母线不相交,取x2=d。
②当水平面与弹轴交点C在图5中C2到C3区间时,水平面与下母线交于圆柱段;而且与上母线不相交,所以取x1=a,x2=d。
③当水平面与弹轴交点C在图5中C3到C4区间时,水平面与下母线交于圆柱段,取x1=a;水平面与上母线交点由方程确定:
(39)
其中必有一解xb在a与d之间,所以取x2=xb;同时在该区间内R1=(xC-d)tan(θ-δ)<-R0,所以取R1=-R0,则Φ=arccos(-1)=π。
进一步考虑入水冲击时水面抬升现象,如图6所示,引入水面抬升因子,采用等效水面来计算xC值。

图6 弹体击水等效水面
根据图6中的几何关系,有
(40)
式中:Ca为xC的实际值。
假设Z为单位入水深度,Zw为水面抬升因子,则有:
xC=Ce=xCw=xC1-Zw(xC1-Ca)
(41)
式中:Ce为xC的等效值。
在计算过程中采用xC等效值Ce判断积分区域,进行计算。
根据文献[10]说明,水面抬升因子Zw在1.48~1.36之间。
7 Simulink程序计算
利用Matlab/Simulink模块对上述方程进行计算分析。
按照流程图7进行计算。
按照此程序计算如下算例。弹体长度:1 900 mm,弹体圆柱段半径:150 mm,头部曲面母线半径:300 mm,弹体圆顶半径:73.6 mm,弹体质量:150 kg,弹体体积:1.304 5 m3,弹体密度:1 153 kg/m3,质心距弹头端面距离:976.5 mm,质心距弹头与圆柱段截面距离:776.5 mm,弹体赤道转动惯量:43.72 kg/m2,水面抬升因子:1.42,海水密度:1 025 kg/m3,弹体入水速度:170 m/s,弹体入水角度:π/4,攻角:0°,重力加速度:9.81 kg·m/s2。

图7 计算流程图
弹体尺寸以及相关数据如图8所示。

图8 弹体尺寸
根据弹体击水时的实际工况,在弹体高速入水的情况下,一般击水载荷峰值出现在1 ms以内。弹体击水载荷峰值出现在弹体头部下半部曲面以及平顶平面与水完全接触时,则计算的xC值上、下限区间如图9所示。
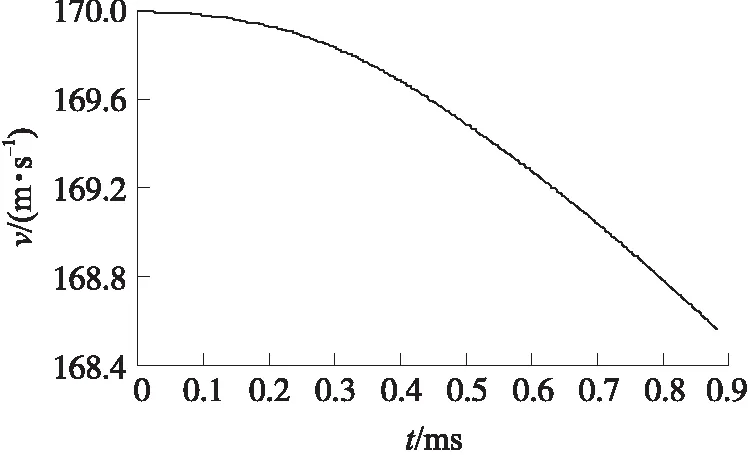
则弹体第一点,即图中左上角弹体上一点与水接触时,水面方程与弹轴线的交点坐标即xC1值为1.05。计算结束时弹体平顶平面上最后一点,即右上角一点与水接触时xC值为0.90。即0.90 图9 xC区间计算图 图10 速度曲线 图11 轴向载荷 图12 径向载荷 图13 力矩 本文基于流体动量定理,对大口径平头弹体击水模型进行简化,并结合弹体入水时的运动学方程,得到大口径平头弹体击水动力学方程组。通过Simulink编写程序进行了一个算例的计算,算例分析结果如下。 ①算例中计算弹体击水时间为0.89 ms,其轴向力达到了420 kN,根据其质量150 kg,得出弹体入水时的轴向冲击载荷达到了280g(g为重力加速度)。 ②径向力先增大后减小,最大值达到了180 kN,径向冲击载荷为120g。 ③由于弹体击水过程极短,径向力力臂基本不变,弹体所受的力矩曲线与径向力曲线基本一致。 得出如下结论: 通过本文得出的大口径平头弹体击水动力学方程组,对150 kg的大口径平头弹体以45°,170 m/s工况入水的算例进行计算,得到了弹体高速入水时所受到的力与力矩。该方法可以为水中兵器强度设计,以及入水载荷问题的研究提供一种物理模型。 目前研究不足之处在于: ①本文在进行理论公式推导过程中做了大量简化处理以及无关性假设,未考虑的因素较多,计算得到的力与力矩结果偏小。 ②弹体击水时的载荷峰值出现的时间以及位置,与弹体的结构特点和入水时的工况有关。本文方程组的计算结果受到积分区间的影响,该方程组无法计算力的峰值的解析解。 因此,本文研究方法与内容对进一步研究该问题提供了一定参考,但后期还需进行更深入的研究。



8 结论与展望
