海岸波浪多次破碎波能耗散模型

2020-10-09闫圣邹志利

海洋学报 2020年9期

闫圣，邹志利*

( 1. 大连理工大学海岸和近海工程国家重点实验室，辽宁大连 116024)

1 引言

海岸波浪在近岸处由于水深变浅会发生破碎，在缓坡海岸波浪还可能发生多次破碎。如在淤泥质海岸，海底坡度通常很小，可从1∶100 到1∶1000 或者更缓，所以极易发生波浪多次破碎。波浪破碎会将波浪运动的动量转化给水流，引起沿岸流和裂流等海岸环流运动。无论是破碎波浪还是海岸环流对海岸地形的形成和演化都具有重要意义：波浪破碎会引起泥沙悬浮和输移；海岸环流会产生不同于潮流的泥沙输移。由于这样的原因，海岸破碎波计算模型的研究一直是海岸水动力研究中的重要课题[1–5]。

目前，对海岸波浪波高的计算经常采用的是波能流方程，该方程是通过在波能守恒方程中加入表达波浪破碎影响的波能耗散项来建立的。现有的波能耗散项的表达存在两种类型：一是将波能耗散等价于溃坝时的水跃能量耗散[1,3]；二是设波能耗散正比于波能和稳定波能之差[2,6]（稳定波能对应于具有常数波高的破碎波，一般仅存在于水深为常数的情况）。这些模型的不足之处是都不能考虑缓坡海岸上的波浪多次破碎及波浪恢复过程。前者模型显然无法考虑波浪恢复情况，因为该模型成立的前提是波浪已经破碎；但后者模型中隐含了波浪可以不破碎的情况，即波能和稳定波能之差为0 或者值很小的情况，但这一情况实际上并不能发生，因为稳定波能仅在常数水深存在，而海岸水底总是存在坡度的。所以，为了使现有模型能够考虑多次波浪破碎和波浪恢复，需要对现有波能耗散模型进行修正，本文拟基于上述第二类模型（Dally 模型[2]）给出新的波能耗散模型。

本文首先从包含波浪恢复的需要出发，给出了Dally 波能耗散模型中稳定波能和波能耗散系数的重新确定方法；然后以此为基础建立了新的波能耗散表达式和波浪破碎过程中波浪恢复的判断条件；最后进行了模型对比验证，将新模型计算的波高与平面斜坡海岸和沙坝海岸的破碎波波高实验结果进行了对比，同时与其他模型的计算结果进行了对比。

2 波能耗散表达式的建立

对于海岸和波浪在沿岸方向都是均匀的情况下，Dally 模型[2]的波能方程具有如下表达式（对应在x轴指向离岸方向的坐标系）：

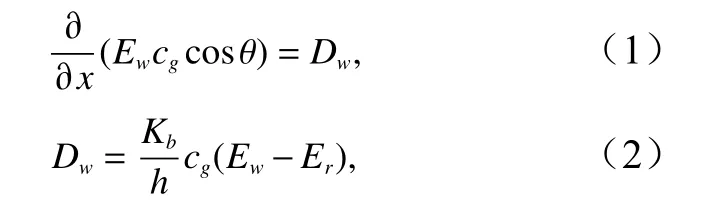
式中，Ew=ρgH2/8为当地波能，H为波高，ρ和g分别是流体密度和重力加速度；Er=ρgHr2/8为稳定波能(或者参考波能）；Dw是波能耗散；h是当地水深； θ和cg分别是波浪相对海岸法线的波向角和群速（前者对平直岸线可采用波浪折射的Snell 定律 sinθ/c=常数来计算）；Kb是波能耗散系数；Hr=γr(h+)，γr是稳定波能对应的波高水深比，是平均水面升高（波浪增减水）。在不同的模型中Kb和γr的确定是不同的，Dally 等[2]对不同水底坡度分别给出两物理量的值（对于坡度1∶80～1∶30，γr=0.350～0.475、Kb=0.100～0.275）；Tajima 和Madsen[6]通过先给定常数水深情况 γr，即γr=0.28，然后通过引入饱和破碎波状态（波高水深比γ=γs时∂γ/∂x=0）来确定Kb，这样做的优点是：所得到的Kb具有解析表达式，即可以得到Kb对水底坡度的解析关系，即

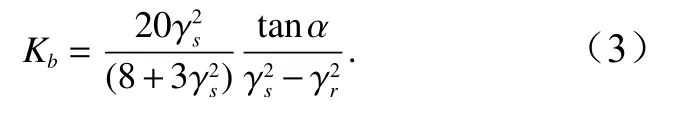
在这一模型中，饱和破碎波状态的引入是关键，这一状态的特征是波高水深比 γ=H/(h+)为常数。Tajima 和Madsen[6]通过实验确定的这一常数值为γs=γr+4tanα，tanα为水底坡度。在以上模型中，γr和γs都是对应于饱和的破碎状态：前者对应于平底情况，后者对应于斜坡情况（本文将保留这两个参数，但将给出不同的表达式）。

本文中新模型的建立主要以Tajima 和Madsen[6]的波能耗散公式为基础，但所采用的推导思路与这一模型是不同的，Tajima 和Madsen[6]是先给定Er，然后确定Kb，而本文是先给定Kb，然后确定Er。Kb的给定是基于事先假设（以计算波高与实验波高相符合为标准），而Er的确定是基于使波能耗散Dw在波浪恢复区为0 或者具有很小值的假定。这一推导思路的优点是它可以克服Tajima 和Madsen 模型只能包含γ>γs的非饱和状态和γ=γs的饱和状态，而不能包含波浪恢复状态的缺点。在后一状态中，波浪不再破碎，对应的波能耗散趋近于0：Dw→0。本文从有关实验结果[7–8]（对应的海岸坡度为1∶100）和Ruessink 等[9]在美国北卡罗来纳州的Duck 海岸（含沙坝）的现场观测发现，这一波浪状态对应的波高接近常数，基于这一观察，新模型克服上述缺点的方式是：首先将波浪恢复区域Dw=0作为Dw的最小值引入到Dw的表达式确定中，然后放宽这一条件，来克服这一条件仅能在平底情况实现的问题，即令在波浪恢复区域Dw不是等于0，而是具有很小的值（Dw→0），这样可以考虑水底坡度引起的波浪变浅作用。实现这一目标需要重新定义稳定波能Er或者 γr（仍然定义为此，在Dw的表达式（2）引入条件：在时，Dw→0。从而得到新的稳定波能Er的表达式为即在Er的表达式中将 γr替换为显然，这一改变会使Dw的表达式中Ew−Er的值在时是趋于0 的，这也表明时波浪恢复开始发生，所以本模型选取作为波浪恢复的判断条件。这里是一个需要由实验确定的量，本文的结果为

以上Er表达式的改变意味着需要重新确定Kb的表达式，因为以上处理使得Er的值增大了，从而使Ew−Er的值减小了，这样为了保持Dw的值（基本）不变，Kb的值就需要相应的增大。这里通过将Kb表达式乘以因子1+20tanα来实现，该因子的适用性可以由波高的计算结果与实验结果符合得到验证。乘以因子后，再令（对应上面确定Er的条件），则可得Kb的新的表达式为

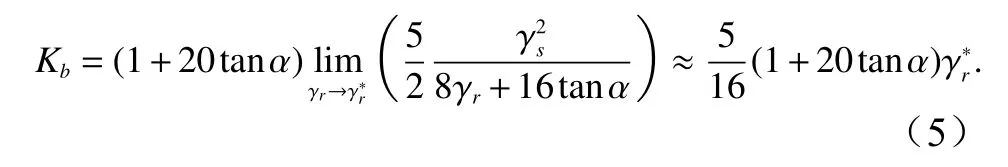
以上推导的目的是想通过令波能耗散为0（Dw→0）来建立波浪恢复区（起始点在处），但当考虑海岸实际为变水深（坡度为 tanα），则在波浪恢复区波能耗散不能为0，而应当为一小量，因为如上所述，实验测得的波浪恢复区的波高近似为常数，要实现这一点就需要一定的波能耗散来抵消水深减小引起的波高增大（即波浪变浅作用），这可以从方程（1）的以下形式看出（考虑 θ=0波浪正向入射的情况）：

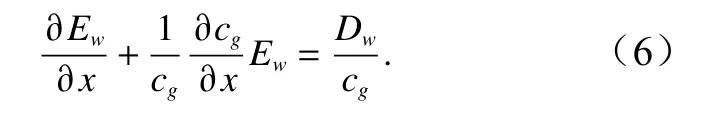
由于波浪恢复区波高近似为常数，有∂Ew/∂x=0，所以在该区域有Dw=(Ew/cg)∂cg/∂x，即Dw在波浪恢复区不为0，而保持为一有限值，这样就可以实现克服斜坡上波高随着水深变浅而出现的增大。物理上，该波能耗散的来源可以认为是波浪破碎区产生的湍流扩散到波浪恢复区所形成。这样，为了实现这一非零Dw，需要将上面引入的稳定波能进行适当减小，以使得在时满足Dw>0。

为此，可在以上Er的表达式中将乘以一个小于1 的因子 Γs，即

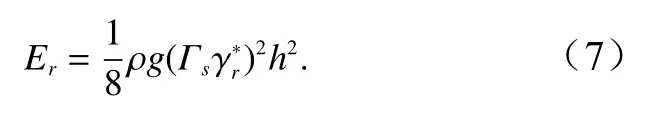
如上所述，该因子的作用是使Dw能够抵消波浪变浅作用影响，所以这里将其称为变浅作用因子。对海底为平面斜坡情况，该因子是存在解析表达式的，这可从将Dw表达式（2）代入到方程（6）后看出。下面分两种情况给出结果：

（1）在波浪恢复区，由于在波浪恢复区波高近似为常数，有dEw/dx=0。另外，Er可表达为（应用为处水深）。将这些结果代入方程（6），并利用和∂h/∂x=tanα），则可得到Γs在波浪恢复区的解析表达式为

（2）在波浪破碎区，对波浪恢复区以外的波浪破碎区也同样可以引入因子 Γs，即Er的表达式（7）仍然成立，因为在这些区域同样存在波浪变浅作用。除这一含义外， Γs的引入还具有另一个物理意义，即其对应于饱和波高水深比 γs的新值，即

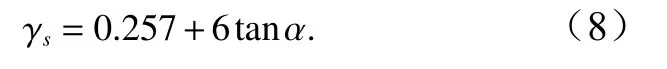
鉴于 γs代表波高水深比随水深变小的极限值，并且在以上推导中已经将 γr用代替，所以 γs的值相应的要有所改变，即需要用以上式（8）新值取代Tajima 和Madsen[6]的饱和波高水深比 γs。以上 γs的引入使得波浪破碎区内 Γs的表达式可以确定，即将 γ=γs饱和破碎波处作为方程（6）的边界条件来得到式（7）所含的常数的 Γs的表达式。利用这些条件，有再利用上面引入的结果 (1/cg)∂cg/∂x≈tanα/2h，将式（2）代入方程（6）即可得到

合并以上两个区域的结果可得 Γs表达式为

式中，在波浪破碎区，对一般水底坡度 tanα=1∶10～1∶100， Γs的值接近于1，范围为0.86～0.92；在波浪恢复区， Γs依赖于水深（与水深成反比）。

应用以上公式时需要确定波浪恢复区所在范围。恢复区的起点可由上面推导的第一步骤所采用的条件时Dw →0来确定，即恢复区发生的条件为（γ 由计算，H由方程（1）计算）。从这一点开始，波浪破碎停止，波高不再衰减，而是近似保持常数。但随着水深的变浅，这一波高将会超过波浪破碎的临界波高Hb=γbh，将发生再一次的破碎，这标志着波浪恢复区的结束，因而波浪恢复区结束的判断的条件是： γ=γb。由此可确定恢复区的宽度：

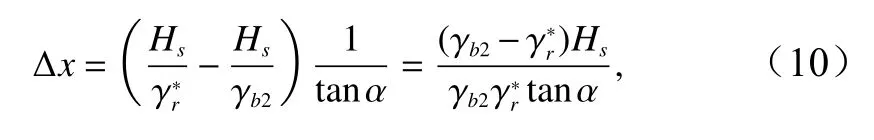
式中， γb2是波浪第二次破碎时的波浪破碎指标，而波浪破碎指标 γb可采用下式计算[6]，即

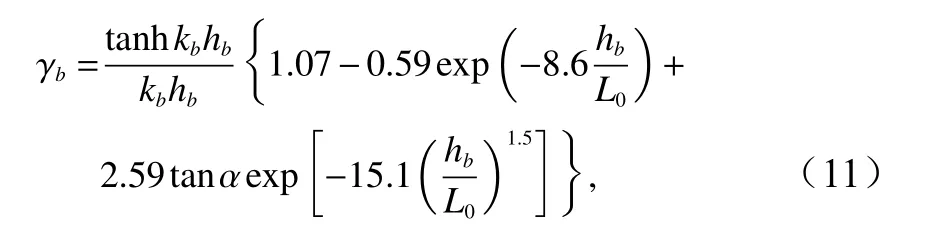
式中，hb是波浪开始破碎处的水深；kb是水深hb处的波数；L0是深水波长。对第一次波浪破碎也可以采用该判据。由式（10）可见，水底坡度越缓（ tanα越小），波浪恢复区越长，如对模型实验情况，tanα=1∶100 和Hs=0 .02m，则 ∆x≈2m。

以上所建立的波浪恢复区仅存在于规则波情况，对不规则波，在统计意义上说是不存在这样的区域的，因为不规则波波列包含不规则出现的大波和小波，大波形成的波浪恢复区会被小波的波浪破碎区所覆盖，因而对一固定空间点不可能总是保持为波浪恢复状态，所以稳定的波浪恢复区是不存在的。

为了进一步对上述模型建立的物理原理进行直观的解释，图1 给出了平坡海岸对应不同水底坡度（1∶40、1∶70、1∶100、1∶250、1∶500）的波高变化和对应的波高水深比，图中波高为通过以下公式将计算所得波高H转化为包括非线性影响的波高式中d1和d2的表达式见文献[6]。由波高变化结果可见，对坡度1∶40 和1∶70，波浪仅发生了一次破碎，而对坡度1∶100 发生了两次破碎，对坡度1∶250 和1∶500 发生了3 次和4 次破碎。其中，波浪发生两次和多次破碎可由波高计算结果出现波高衰减的结束并且转化为近似常数的变化来看出。为了说明这些波浪破碎状态的正确性，对坡度1∶40 和1∶100 还给出了对应的实验结果。实验结果中的1∶100 坡度波浪发生了两次破碎，而坡度1∶40 波浪仅有一次破碎，这与计算完全符合，说明计算结果是可靠的，也说明本文所建立的波能耗散模型的合理性。为了此目的，图中还给出了对应不同水底坡度的的水平线，由这些直线可以看出本文模型的波浪恢复区判断条件的适用性。因为图中仅在波浪发生两次及多次破碎情况（坡度1∶100、1∶250、1∶500），计算的 γ曲线（由γ=H/(h+)计算得到）才在波浪恢复区与这些直线重合，即符合了条件而在波浪仅发生一次破碎的情况（坡度1∶40、1∶70），计算的 γ曲线始终高于直线不与其重合，所以不符合条件这说明了用作为判断波浪恢复发生的条件是适合的。图中波浪恢复状态的结束可由图中波高重新开始衰减看出。在图中，坡度1∶500 情况出现了多个恢复区，而且恢复区离海岸线越近，其宽度越小。这一特征可从式(10)看出：离海岸线越近，Hs越小，因而 ∆x越小。由图1 也可以看出， γ值随着离岸线距离的变小而趋近一常数，这一状态即是上面所提到的饱和破碎波，其特征是波高与水深成正比，即 γ等于常数，对应的γ即是式（8）中饱和波高水深比 γs。

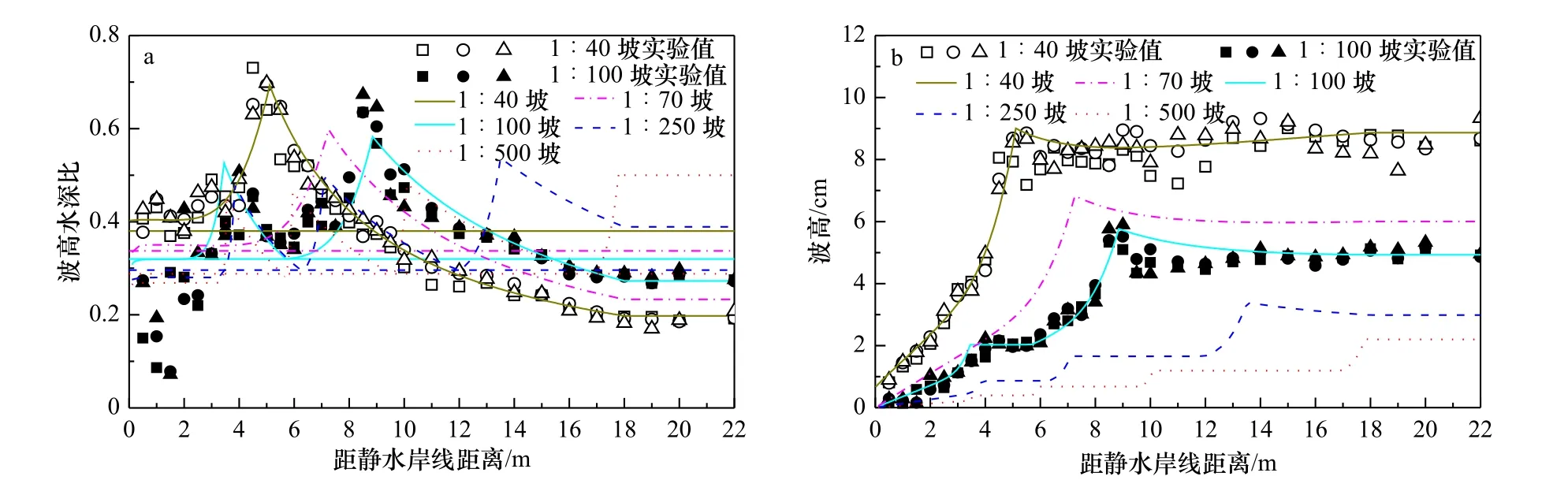
图1 不同海岸坡度情况波高水深比（a）和波高（b）在垂直海岸方向的变化Fig. 1 The cross-shore variations of wave height-depth ratios (a) and wave heights (b) calculated by the presentmodel for different typical slopes

3 模型验证

以上建立的波浪耗散模型所包含的物理量的表达式都是与以往Dally 型波能耗散[2,6]所采用表达式不同的，它们包括稳定波能Er表达式（7），波能耗散系数Kb表达式（5）和饱和波高水深比表达式（8）。为了验证这些表达式的适用性和新波能耗散模型的有效性，下面给出由该模型得到的波高计算结果与实验结果的对比。为了说明新模型可以适用于一般海岸的情况，对比采用的波况包括了不同的水底坡度、不同的入射波高和周期，也包括了沙坝海底地形情况。较缓坡度1∶100 和1∶40 实验取自文献[7–8]，较陡坡度1∶20 和1∶10 实验取自文献[10]。

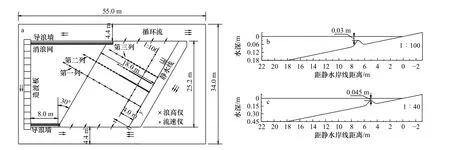
图2 实验布置平面图（1∶100 平坡海岸，1∶40 坡的与此相似）（a）和沙坝海岸横剖面（b，c）Fig. 2 The plan view of experimental layout (1∶100 plane beach, similar for the slope 1∶40)(a) and the vertical profiles of barred beaches (b, c)

文献[7–8]的实验在大连理工大学海岸和近海工程国家重点实验室的波浪水池（长55.0m、宽34.0m、深0.8m）进行，布置见图2，采用的波况见表1。实验中波浪是以30°角斜向入射到海岸，所以实验中的海岸模型与造波板有30°的夹角。波浪斜向入射意味着流场中除了波浪还存在着波浪破碎产生的沿岸流。海岸模型包括1∶100 和1∶40 两个坡度，它们的海岸宽度都为18m，但坡前水深分别为18 cm 和45 cm。每个坡度包括平坡和沙坝两种地形，沙坝横剖面为高斯型的，其中心距岸线距离在1∶100 坡海岸为7m、在1∶40 坡海岸为5m，坝顶距静水面的距离分别为3 cm 和4.5 cm，如图2 所示。波浪类型包括规则波和不规则波。不规则波采用JONSWAP 谱。波面升高测量断面有3 个（y=7.0m，12.0m，17.0m），具体布置见图2，计算结果对比采用的是中间断面的数据。Visser[10]的实验与上述平坡海岸实验类似，但海岸坡度为1∶20 和1∶10，入射角包括30.5°和15.4°。

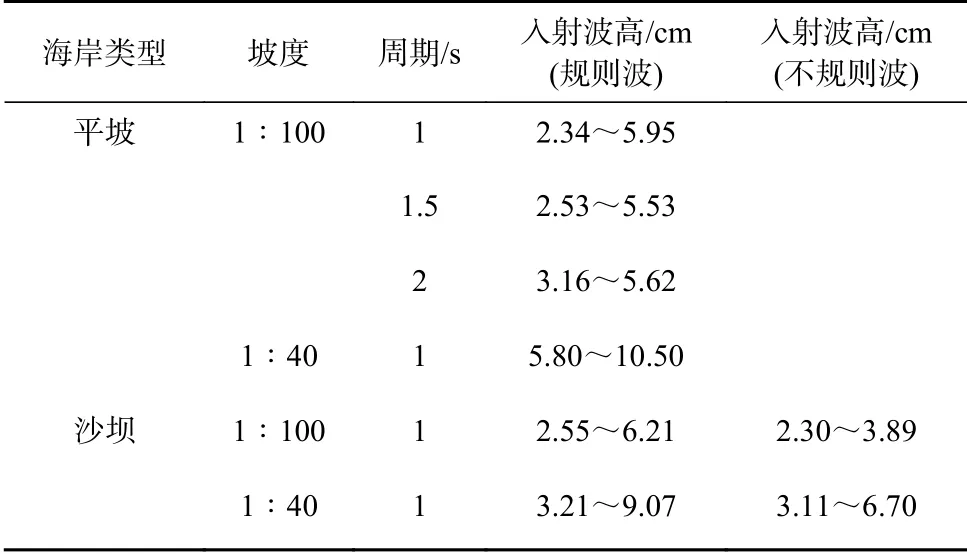
表1 实验波况[7−8]Table 1 Test condition[7−8]

图3 是平坡海岸的波高结果对比。因为二次波浪破碎和波浪恢复现象仅在规则波情况发生，所以这里仅给出规则波情况的结果。对比针对从较陡水底坡度到较缓水底坡度（1∶10～1∶100），波浪包括不同波高和周期。其中，1∶100 坡度海岸发生了二次波浪破碎和波浪恢复现象，波浪恢复区在图中由两竖虚线标出，第一条代表第一次波浪破碎的结束和波浪恢复区的开始，第二条代表波浪恢复区的结束和第二次破碎的开始。对于1 s 周期3 个不同的波高，入射波波高越大，波浪的恢复区长度越大；对于相近的入射波高，不同周期波浪恢复区的长度接近。对其他坡度的情况，仅有一次波浪破碎，没有发生二次波浪破碎。对图中的每个算例，计算结果和实验结果的符合程度都是很好的，表明本研究建立的新的波能耗散模型对不同的水底坡度、不同的入射波高和周期都有很好的适用性。这也验证了本模型引入的稳定波能Er的表达式（7）、波能耗散系数Kb的表达式（5）和饱和波高水深比表达式（8）的适用性。尤其值得注意的是，本文模型对波浪恢复状态的计算结果具有很好的适用性，这包括：（1）波浪恢复开始点判断的准确性。这一判断是由条件 γ=γ∗r得到的，这表明了该条件的有效性；（2）波浪恢复区内波高结果的精度。所计算的波高近似为常数，这与实验测量结果的变化趋势是一致的；（3）波浪恢复区宽度的精度。可以验证，其也符合式（10）的结果。图中还给出了由Tajima 和Madsen[6]模型计算得到的结果。该模型事实上不能考虑波浪恢复，在波浪恢复区其给出的波高仍然是衰减的，为此，计算中采用了人为干预，即对存在波浪恢复区的1∶100 坡度情况在波浪恢复区人为令Dw=0。由此得到的波浪恢复区的波高并不是保持为常数，而是有增大趋势，这与实验不符合。这是因为事实上在波浪恢复区Dw并不是0 而是需要保持一很小值以便抵消波浪变浅作用导致的波高增大。对不发生波浪二次破碎的情况，不需要以上处理，该模型与实验结果符合是很好的，与本模型与实验符合情况类似。

图4 和图5 是沙坝海岸波高结果的对比。海岸平均坡度为对应文献[7–8]的1∶40 和1∶100，沙坝剖面见图2b 和图2c。计算中，水底坡度 tanα需做特别考虑：对Kb将其取为海岸的平均坡度，即1∶40 或者1∶100；对Γs将其取为当地地形坡度，即t anα=∂h/∂x。这样，在沙坝背浪侧 tanα将为负值，其物理意义与取正值情况一样，仍然反映的是浅化作用的影响，只不过这时对应的是波高减小而不是正值情况的波高增大。波浪恢复起始点仍然由条件 γ=γr∗来判断。

与平坡情况不同，沙坝海岸的波浪恢复和二次破碎是容易判断的，因为在沙坝后方的凹槽区域由于水深快速增大，波浪恢复一定发生，同时，伴随恢复区结束将出现二次破碎。这一恢复区的另一特征是其容易在数值模拟中考虑，因为现有的波能耗散模型是通过将规则波的波能耗散乘以波浪破碎的概率函数Qb而形成的，例如Roelvink[3]给出的模型Dw=2αfpEwQb（fp是谱峰频率，α为常数）和Church 和Thornton[11]的模型

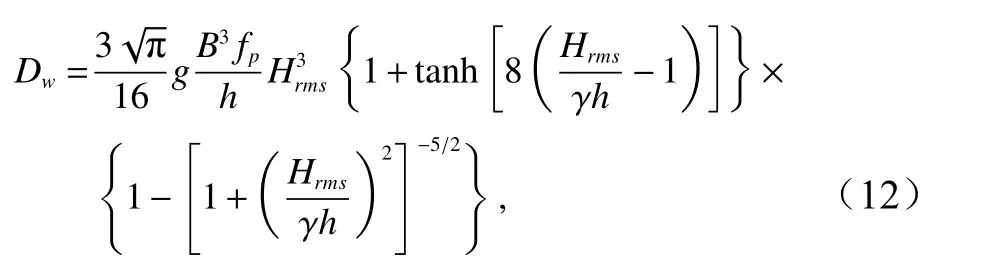
式中，γ=0.43；B≈0.9。上式中除了因子外的其他部分可看作概率函数Qb。由于在沙坝凹槽区水深较大，概率函数Qb快速减小而具有很小的值，这导致在这一区域波能耗散Dw也具有很小的值，所以可以实现波浪恢复现象。为了说明这一点，图4 给出了坡度1∶40 规则波和不规则波情况的本模型和Church和Thornton[11]模型计算的波高和波能耗散。可见，在沙坝坝峰之后一直到发生二次破碎，波能耗散Dw一直可以保持很小的值，对应的波浪恢复区波高近似保持常数状态，而且Church 和Thornton[11]模型与本模型的Dw值很接近，这说明像Church 和Thornton[11]这样的波能耗散模型对沙坝地形是可以考虑波浪恢复状态的，尽管其没有在模型建立中对此给出特殊考虑。但与这类模型相比，本模型还是具有更为精确的优点，这体现在本模型可以考虑沙坝凹槽一侧斜坡到第二次破碎发生处地形变化引起的波浪变浅作用，这是由式（9）中波浪恢复区的因子 Γs来实现的，其在沙坝凹槽一侧斜坡上导致Dw为负值（因为 tanα=∂h/∂x<0），而在这之后的平坡上为正值（因为 tanα=∂h/∂x>0）。前者虽然波能耗散为负的，但方程（6）左端的波浪变浅作用项 (1/cg)∂cg/∂x=htanα/2也是负值，所以二者是相互抵消的，使得方程（6）仍然能给出∂Ew/∂x=0，即在波浪恢复区波高为常数。在凹槽之后的平坡区域方程（6）也具有∂Ew/∂x=0，这使得图中本模型的波高计算结果要比Church 和Thornton[11]模型的更接近实验结果，后者由于人为设定Dw=0，从而无法抵消波浪恢复区的波浪变浅作用项，因而给出的波高并不是常数。对坡度1∶100 的地形也有这样的结果，见图5。

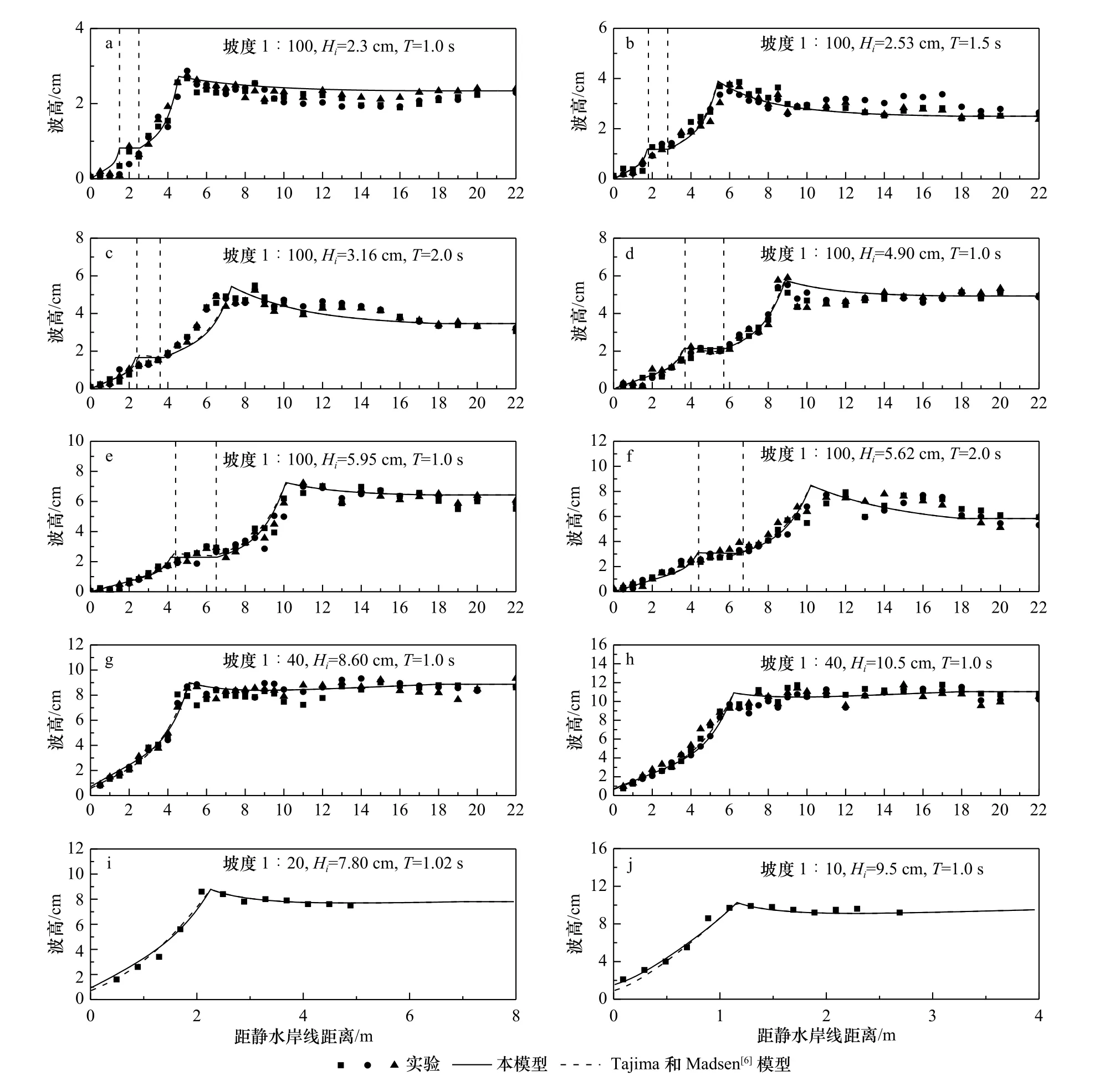
图3 平坡海岸波高的计算结果和实验结果的对比(规则波情况）Fig. 3 Comparison of computed andmeasured cross-shore wave heights for regular waves

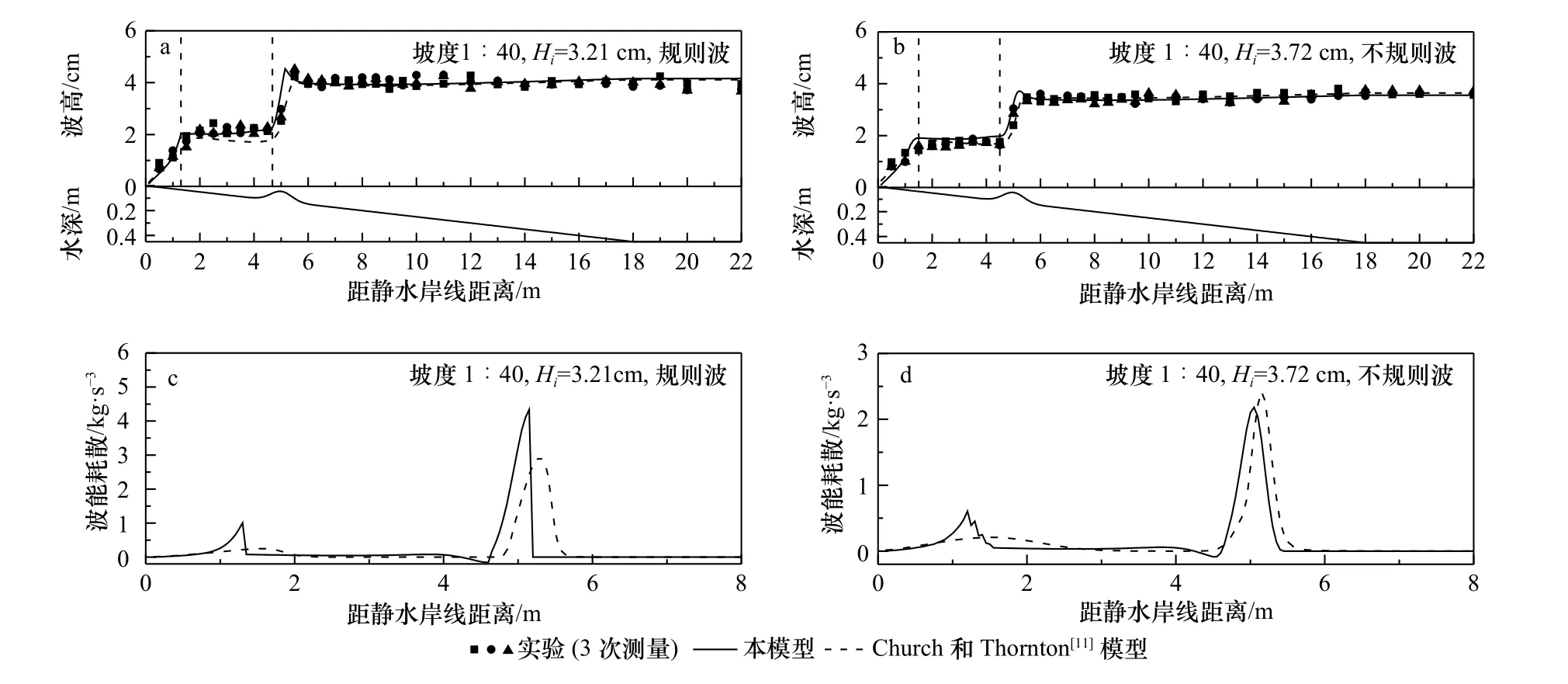
图4 沙坝海岸规则波（a，c）和不规则波（b，d）的波高和波能耗散空间变化形态（坡度1∶40）Fig. 4 Cross-shore variations of wave height and energy dissipation on barred beach with slope 1∶40 for regular wave (a, c) and irregular wave (b, d)

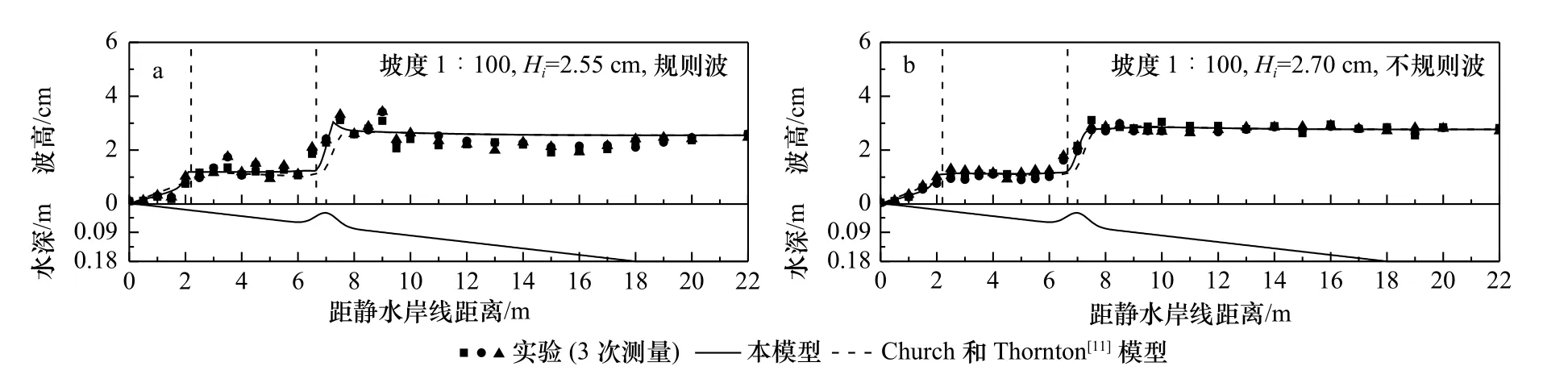
图5 沙坝海岸规则波（a）和不规则波（b）的波高空间变化（坡度1∶100）Fig. 5 Cross-shore variations of wave height on barred beach with slope 1∶100 for regular wave (a) and irregular wave (b)

由以上分析可见，Church 和Thornton[11]模型（以及类似模型）之所以能识别波浪恢复区是因为概率函数Qb随水深变大而值变小的特征，而沙坝凹槽区恰好能实现这一特征，所以沙坝海岸的沙坝凹槽区的波浪恢复能够被这类模式识别的。但平坡海岸波浪恢复区水深逐渐变小（如图3 中情况），这类模型不能给出平坡波浪恢复区的波浪演化，只能给出像破碎区一样的衰减结果。