基于水龄熵的矿井防尘供水管网可靠性研究
2020-10-09彭亚蒋仲安王佩
彭亚,蒋仲安,王佩
(1.北京科技大学土木与资源工程学院,北京,100083;2.首都经济贸易大学管理工程学院,北京,100070)
矿井防尘供水管网是地下矿山开采的重要基础设施,其可靠有效运行是井下粉尘防治、矿工安全健康以及生产正常运行的重要保障[1]。由于矿井防尘供水管网工作压力较高,以往研究主要着眼于其水力可靠性[2-3],而对水质研究尚有不足。防尘管网(如管段、部件)的使用寿命以及矿井生产和安全相关的诸多用水设备设施的性能,不仅受水力条件影响,也与管网的供水水质息息相关[4-6]。管网机械性能下降会进一步影响管网的水力工况,导致无法满足井下用水需求。水在管网中的滞留时间越长,水体与管壁、微生物等发生物理、化学及生物反应的机会更多,管道及部件的腐蚀风险也随之增大,在矿井防尘供水管网高水压条件下日积月累,进一步增加了爆管漏损的风险。水龄,其定义为水在管网中的滞留时间,是能够反映水质条件变化的重要指标,以往研究表明水龄条件与管道腐蚀速率密切相关[7-10]。此外,矿井供水管网虽然主要用于提供井下防尘等生产用水,但在特殊或者紧急避险条件下,也作为被困工人的生命水源。随着2010年国家对完善矿山井下供水施救系统建设的强制推行,如济宁三号煤矿等矿井将供水施救系统与防尘供水系统进行合建、共用管路,在应急情况下实现井下饮用水与生产用水转换。因此,在研究矿井防尘供水管网可靠性时,将水力水质条件进行综合考虑具有一定的必要性。
供水管网可靠性的分析方法主要可以分为解析法、模拟法、代理指标法3大类。解析法主要包括故障分析法[11]、层次分析法[12]和拓扑可靠性分析法[13]等,通常先利用枚举法选择状态,再通过数学推导的方式计算可靠性;模拟法以蒙特卡罗法[14-15]、拟蒙特卡罗法[2-3]为代表,利用静态或者动态水力模拟方法模拟管网系统不同工况条件,分析管网在指定时间内以一定服务水压供给用户所需水量的概率,并按照事先对可靠性的定义计算出供水管网的可靠度;代理指标法是采用简化的数学模型替代复杂的仿真或解析模型,求解出与原仿真分析模型相近的结果,从而减少计算量和计算时间,大幅提高评价分析的效率,该方法主要包括能量熵、流量熵和可恢复力指标法等[16-19]。
上述可靠性分析方法多用于研究有压多环市政供水管网,且以水力可靠性研究为主,并且在对矿井防尘供水管网的研究上常使用解析法和模拟法,而代理指标法鲜有报道。此外,现有文献中有关矿井供水管网的水力可靠性研究多围绕静态水力工况,而较少研究动态水力工况和水质条件。针对矿山井下用水随生产安排动态变化的特点,本文作者将模拟法与代理指标法相结合,基于信息熵的基本思想和水力水质动态模拟方法,在路径流量的基础上引入水龄评价指标,构建矿井防尘供水管网可靠度评价模型;并基于MATLAB 编程平台,调用EPANET 水力水质模拟引擎,实现动态水力水质条件下评价模型的联合求解,以期作为矿井防尘供水管网传统水力可靠性研究基础上的重要补充,并进一步为管网的优化研究提供参考。
1 防尘管网可靠度评价模型构建
1.1 信息熵原理
熵的概念首先由德国物理学家CLAUSIUS[20]提出并将其用于描述热力学第二定律。1948年,现代信息论创始人SHANNON等[21-23]首次将熵的概念引入信息论中,定义信息熵表征信源的不确定性,其表达式如式(1)所示。AWUMAH[24-25,18]等将信息熵原理和管网路径、管段流量信息相结合,应用到管网可靠性研究中,本文引入管网水龄条件进行扩展,推导水龄熵和可靠度计算公式,构建综合了水龄、流量和拓扑结构的矿井防尘供水管网可靠度评价模型。

式中:H(X)为信息熵;X为随机变量,{x1,x2,…,xn};C为任意正常数,通常取1;p(xi)为事件xi发生的概率,且满足
1.2 水龄熵模型
假设供水管道中物质组分的演变为一维对流传输过程,根据物质质量守恒和物质成分的反应动力学,可以建立微分方程式
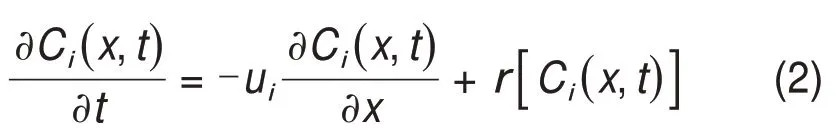
式中:Ci(x,t)为在t时间,管段i的纵向x处的反应物浓度;ui为管段i的平均流速,m/s;为管段中反应物质的反应变化速率,对于不同的反应物质可选用不同的反应模型。
水龄可以被处理为一种反应成分[8],在管网系统中发生零级动力学反应,结合式(2)可得到管段中水龄反应满足
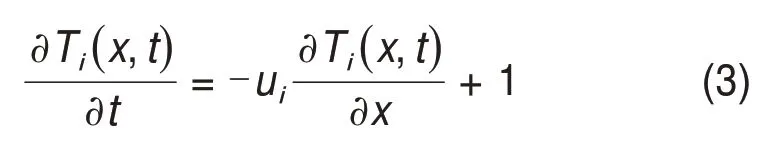
节点是水流汇聚与重新分布的连接点,对于无容节点,节点水龄通过水在该节点不同的水源供水路径所经历的不同时间的加权平均值求得,即

式中:i表示流出节点j的管段;K为流入节点j的管段k的集合;Ti(0,t)为在t时间,节点j的下游管段i起点处的水龄;Qk为管段k的流量,m3/s;Tk(xj,t)为在t时间,管段k末端与节点j相连处的水龄。
由式(4)可知,无容节点汇入总流量与节点的水龄的乘积等于各上游管段流量与该管段末端水龄乘积之和。参考TANYIMBOH 等[25]在供水管网研究中提出的路径概念,可以得式(5)。基于信息熵定义式(4),构建水龄熵的概率空间如式(6)所示。

式中:n为节点j的路径数;为节点j第i条路径的路径流量,L/s;为水通过第i条路径到达节点j的终端水龄;qj为流入节点j的路径流量之和,L/s;Tj为节点j的水龄。
从而可以定义水龄熵Sj为
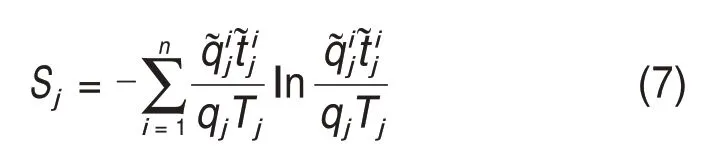
为了求解式(7),对其进一步的推导变换:设管网中任一节点j,在任一时间水源到该节点总路径数为n,流入节点j的总路径流量为qj,其各路径流量集合为{qj},i∈(1,n),各路径终端水龄为节点j相连上游节点分别为x,y和z,各上游节点与节点j相连管段的流量为Qxj,Qyj和Qzj,节点j的路径中经过x,y和z的路径流量集合分别为
流入节点j的总路径流量应该要等于节点j的实际流入管段总流量,即

根据信息熵具有累加性的性质,节点j的水龄熵式(7)可以写成如下形式

对于3个上游节点,根据式(7)可得各自的水龄熵为

根据式(3)可以得经过x,y和z其中一节点通往节点j的各路径下的水龄满足

式中:为水通过第i个路径到达节点j的终端水龄;和分别为水通过第i个路径达到节点x,y和z的终端水龄;txj,tyj和tzj分别为水从节点x,y和z流到节点j所需的时间。
又由式(5)可得对于经过x,y和z的路径分别有

式中:Txj,Tyj和Tzj分别为节点x,y和z到节点j之间的管段终端水龄。
将式(8),(10),(11)和(12)代入式(9),可以对式(9)中各项进行换算,最后得到水龄熵计算公式的一般形式为

式中:Sj为水龄熵;Dj为节点j的上游相邻节点集合;Qxj为上游节点x输送到节点j的流量,即管段xj流量,m3/h;Txj为管段xj终端水龄;Qj为汇入节点j的管段总流量,m3/h;Tj为节点j的水龄。
1.3 节点可靠度
为了提高评价结果的准确性和可比性,对评价结果进行归一化,引入最大水龄熵指标,即将路径水龄平均分配时的水龄熵定义为最大水龄熵,代表了在理想状态下无容节点从每个路径获得的水体的水龄条件具有相同的不确定性,其取值只与上游路径数有关,而上游路径数又由管网拓扑结构和流量决定。取水龄熵和最大水龄熵的比值定义为节点可靠度,从而得到防尘管网节点可靠度计算公式为

式中:Rj为节点j的可靠度;Sj,max为最大水龄熵。
1.4 系统可靠度
进一步对有J个节点的矿井防尘供水管网的系统可靠度定义为

Rj和越接近1,分别表示节点或管网系统的可靠性越强;反之则越不可靠,从而可以据此对管网可靠性较差区域和时段进行重点监测与维护。在实际应用中,可以根据用水点在生产实际中的重要性设置各节点权重系数wj,从而获得最终加权平均系统可靠度,其表达式为

2 防尘管网可靠度评价模型求解
为了实现对上文所构建防尘管网可靠度评价模型的求解,基于MATLAB 编程平台,调用EPANET动态链接库作为水力水质计算引擎[26],编写了模型求解程序。求解流程如图1所示。求解该程序的基本思想是:
1)在MATLAB 环境下加载管网的基本信息,如拓扑结构、节点标高、水池水位、管长、管径和阻力系数等;
2)设置用水点需水量、水力水质模拟时长和步长、反应级数和系数、初始水质参数等;
3)调用EPANET 模拟管网的动态水力水质,获取各节点和管段不同工况下水力参数和水质演变参数;
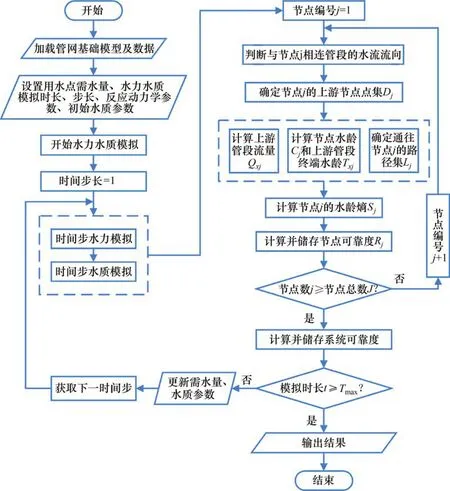
图1 矿井防尘供水管网可靠度评价模型求解流程Fig.1 Flow chart of solving the reliability evaluation model of mine water supply network for dust control
4)在每1个工况下,判断管段内水流流量及方向,确定每个节点的上游节点、上游管段和路径集;
5)根据前文构建的评价模型求解每个节点水龄熵、节点可靠度以及系统可靠度。
3 实例应用
3.1 管网概况
将该可靠性分析模型应用于开滦集团某煤矿井下防尘供水管网,该矿供水管网为多水源重力输送供水管网,以地面静压水池作为供水水源,共有3个静压水池,包括综采、炮采、综掘、炮掘及开拓共17 个井下工作面。经简化,管网拓扑结构及节点管段基本信息如图2所示,由图2可知:该管网共有20个节点,20根管段,12个主要用水节点,管径为108 mm。通过连续监测7 d各类工作面用水量,计算出各类工作面的平均日防尘用水量变化数据,并进行水力水质模拟,各类工作面用水情况如图3所示。
3.2 结果分析
使用MATLAB(R2018b)编程并调用EPANET(V2.0)对上述防尘管网进行了48 h动态水力水质模拟,获取管网节点和管段在不同时间的水力水质数据,然后基于前文的数学模型,求解管网可靠性数据。矿井总用水量最高时管网各节点的水龄分布如图4所示,其中节点1~3为水源节点,水源水龄定义为0 h,各非水源节点在用水最高时的水龄范围为1~15 h。相对于其他节点,位于管网末端的节点14~16具有更大的水龄。

图2 矿井防尘供水管网拓扑结构及基本信息图Fig.2 Topological structure and basic information of the mine water supply network for dust control

图3 矿井防尘供水管网总用水量及各类工作面时用水量变化Fig.3 Water consumption of the mine water supply network for dust control and different working faces
3.2.1 不同节点可靠度分布
为研究不同节点可靠度的分布情况,统计分析整个模拟时段内各非水源节点可靠度,求出最大值、最小值、平均值、上四分位数和下四分位数,然后绘制各非水源节点的可靠度箱形图如图5所示。
从图5中可见:在48 h模拟期间内,该防尘管网节点可靠度大部分在0.5以下,说明该管网可靠性还有较大的提升空间。整体上来看,节点8的可靠度相对其他节点更高,其平均可靠度为0.463 1,分析其原因主要包括:
1)节点8 附近有综采工作面,根据图3可知,该类工作面用水量较其他工作面更大,从而管路流量大;

图4 矿井总用水量最高时各节点水龄分布图Fig.4 Distribution of water age at the period with highest total water consumption
2)节点8处于该管网系统的环状网络上,上游流入水源来自地面3个水池,下游连接多个用水节点,因而流经节点8的路径上,水质更新较快,可靠度也更高。
节点18,19 和20 的可靠度为0,这是因为,该3 处节点为单路径节点,节点18 与1 号水源相连,节点18,19和20之间又依次相连。关于单路径节点的可靠度,在后文中将进一步分析。
3.2.2 不同时间可靠度分布
为研究防尘管网可靠性随时间的变化规律,统计分析每个时间的节点可靠度,绘制各时间可靠度箱形图如图6所示,各时间的系统可靠度根据式(15)计算。由图6可知:在48 h 模拟时长内,各时间管网的系统可靠度均在0.3以下,这一方面是因为同一时间下管网各节点的可靠度离散程度比较大,最大值与最小值相差较大,比如在第16 h,节点可靠度最大值为0.821 2,最小值为0;另一方面是因为可靠度较低的情况比较多,降低了各时间的平均值。
对全部模拟时段防尘管网的系统可靠度求平均值,得到平均系统可靠度为0.180 3,可靠度偏低,其原因很大程度上源自矿井防尘供水管网的结构特征。矿井防尘管网与市政多环管网不同,受采掘计划和工作面布置的限制,防尘管网建设以枝状结构为主,管网中闭合环结构相对较少,串联管路较多,所以求解得到的系统可靠度整体上会比多环管网的可靠度偏低。在矿井防尘供水管网实际建设或改造中,建议增加并联管路或者环状结构来提高管网可靠性,避免为了节约成本只选用单路径供水而带来管网故障或者失效风险。此外,由图6还可见,管网的系统可靠度随时间呈现一定的日周期性,这是因为管网系统的用水情况决定了管段中流速、流量、流向以及水质的更新变化,而矿井用水受生产活动安排影响一般呈现周期性。
3.2.3 系统可靠度和用水量关系
为进一步分析管网系统可靠度和管网用水量的关系,绘制防尘管网总用水量与系统可靠度分别随时间变化的对比图如图7所示。

图5 各非水源节点的可靠度分布箱形图Fig.5 Box-whisker plot of reliability of non-water-source nodes

图6 不同时间的可靠度分布箱形图Fig.6 Box-whisker plot of reliability at different time

图7 总用水量与系统可靠度随时间变化图Fig.7 Variation of total water consumption and system reliability with time
由图7可知:防尘管网的系统可靠度和总用水量随时间呈现出高度一致的趋势,且都呈现出日周期性,说明这两者之间具有较强的相关性。定量分析防尘总用水量和系统可靠度之间的相关性,计算得到Pearson 相关系数为0.814,t检验的显著性概率为小于0.01,拒绝零假设,表明这2个变量之间显著相关,在用水高峰期,管道内流量更大,流速更快,系统水质更新更快,水龄条件更好,可靠度也更高;在用水低峰期,管道内流速相对较慢,水质更新较慢,水龄较大,可靠度因而也较低。
由图7可见,系统可靠度与总用水量的变化趋势并非完全一致,对其进行线性回归分析,得到如图8所示拟合结果。其中拟合优度为0.662 6,说明拟合的方程能解释系统可靠度该因变量66.26%的变化,但还有33.74%不足以解释,2 个变量之间不具有明显的线性关系。
绘制所有用水节点的用水量与节点可靠度散点图如图9所示,由图9可见:用水节点的可靠度与其用水量不呈线性分布,即在矿井日常生产过程中,节点的可靠度并不完全由其自身用水量决定,还受到其他因素的影响。经分析,一方面各节点的用水量都是随时间变化,任一节点的用水量变化的同时,其他节点的用水量也发生变化;另一方面管网拓扑结构会影响上游各路径流量分配,来自各路径水流的水体条件和流量并不相同。

图8 总用水量与系统可靠度的线性回归分析Fig.8 Linear regression analysis between total water consumption and the system reliability
3.2.4 单路径节点可靠度优化
节点18,19和20的可靠度为0,分析其原因:首先从管网结构上来看该节点在整个模拟时段内均为单路径节点,且仅有1号水源供水,一旦管段13 受到破坏,没有其他路径对其供水,用水需求就难以满足;其次从计算原理上分析,在水质模拟时,由于水源初始水龄为0,其水龄熵也为0,所以节点18,19 和20 的上游节点水龄熵为0,从而根据式(14)计算得到节点18,19 和20 的可靠度也应该为0,说明求解结果合理。

图9 用水节点时用水量与节点可靠度散点图Fig.9 Scatter diagram of hourly water consumption and reliability at demand nodes
为了提高该部分节点的可靠性,增加连接管路优化原防尘管网,同时考察管网系统可靠度的变化,即在节点7 号和18 号节点之间新增一条管段,管长为1 000 m,管径为108 mm,粗糙度取100,采用本文所构建评价模型对管网重新分析可靠性。优化后节点18,19和20从只有一个供水水源变为可依水力工况变化从3个水源获取水流,节点平均可靠度从0均增加为0.258 3,且优化后使管网系统中新增了环状结构。对比优化前后不同时间的管网系统可靠度,绘制矿井防尘供水管网优化前后系统可靠度对比,如图10所示。由图10可知:新增管段优化后,明显改善了原管网系统可靠度,管网的平均系统可靠度从0.180 3 增加为0.231 3。由此可知,增加管网节点的供水路径,尤其是形成环状结构,可以有效提高管网的可靠性。
分析结果验证了前文观点,即在对矿井防尘供水管网进行设计或者优化改造的时候,可以增加节点的供水路径或增设环状结构,而不局限于建设传统矿井供水管网的单一路径枝状网络。

图10 矿井防尘供水管网优化前后系统可靠度对比Fig.10 Comparison of the system reliability before and after optimization
4 结论
1)基于信息熵和水力水质动力学机理推导出矿井防尘供水管网水龄熵、节点可靠度和系统可靠度的计算公式,构建了综合考虑管网路径、流量和水龄的矿井防尘供水管网动态可靠度评价模型,可为矿井防尘供水管网的维护管理和优化改造提供参考。
2)基于MATLAB 编程平台,编写了可靠度评价模型求解程序,并调用EPANET 水力水质模拟引擎,对实例矿井防尘供水管网进行48 h 动态水力水质模拟及联合求解,获得了管网在各时段不同工况下的水力、水龄数据及可靠性变化规律。
3)实例矿井防尘供水管网在模拟时段内的平均系统可靠度为0.180 3,其可靠性还有较大提升空间;管网系统可靠度和防尘总用水量随时间的变化趋势高度相关,Pearson 相关系数为0.814,t检验的显著性概率小于0.01,且都呈现日周期性,在用水高峰期,管道流量较大,水质更新较快,系统可靠度也较高,但对具体各节点,其可靠度和用水量没有明显的线性关系。
4)单路径节点17,18 和19 可靠度为0,降低了管网系统可靠性,通过在原管网7 号和18 号节点间新增管段进行优化,可以将平均系统可靠度从0.180 3增加为0.231 3,说明增加节点供水路径,增设环状结构,是提升传统以枝状结构为主的矿井防尘供水管网可靠性的有效方法。
