水田土壤有机碳时空演变下的最优插值方法

乔 婷, 姚彩燕, 于东升, 史学正, 邢世和, 张黎明

(1.福建农林大学资源与环境学院，福建 福州 350002;2.土壤生态系统健康与调控福建省高校重点实验室，福建 福州 350002;3.中国科学院南京土壤研究所土壤与农业可持续发展国家重点实验室，江苏 南京 210008)

土壤在全球碳循环中扮演着重要的角色，全球土壤有机碳(soil organic carbon, SOC)仅变化0.1%就会给大气二氧化碳浓度造成剧烈波动[1].农业土壤碳库是陆地生态系统的重要组成部分，具有易受人为干扰、短时间内可快速调节的特点，其固碳效应可有效延缓全球气候变化[2].农业土壤中的水田由于特殊的淹水条件，固碳效应明显大于旱地[3].我国水田面积超过330 000 km2[4]，占全国粮食作物播种面积的27.4%，占世界水田总面积的23%.太湖地区水稻土分布广泛且剖面发育好，是长江中下游水稻土区中的一个典型[2]，明确该土地利用类型的SOC动态变化对于合理制定全国农业“碳汇”管理政策尤为重要[4-5].由于受土壤类型、母质、地形、气候、生物和农业管理方式的影响，SOC存在明显的时空变异.有研究表明，通过空间插值模型可有效定量化连续土壤属性的时空变异[6].按照不同理论可将常用空间插值法归为非地统计、地统计、互结合3大类，根据数学原理又可分为确定性插值和地统计插值两大类[7].非地统计主要包括径向基函数、反距离权重、样条函数和趋势面分析等确定性方法，以及最近邻函数、TIN三角网和回归树等方法；地统计主要包括普通克里金、简单克里金、泛克里金、析取克里金和指示克里金等；而互结合是基于前两者的拓展方法，典型方法有回归克里金和趋势面分析结合克里金方法等.

目前，很多学者基于不同插值方法对土壤有机碳等属性进行了研究[8-12].如Bhunia et al[8]采用反距离加权、局部多项式、径向基函数、普通克里金和经验贝叶斯克里金5种插值方法，分析了印度梅迪尼浦尔地区同时期3个土壤深度(0～20、20～40和40～100 cm)下SOC的空间变化，表明普通克里金对于表层土是一种均方根误差最小和决定系数最高的较优方法.Addis et al[9]使用普通克里金、反距离权重和径向基函数插值方法，发现在埃塞俄比亚塔纳流域农业区普通克里金下SOC的插值图效果最好，且认为没有一种特定的方法明显适用于pH、质地和有效磷等指标.Li et al[10]对中国西部九台县同年度的土壤有机质、总氮、有效磷、有效钾进行普通克里金、反距离权重、回归克里金插值，发现普通克里金对有机质和有效钾插值效果好.Long et al[11]基于广泛使用的12种插值方法对2008年农业农村部配方施肥项目的235 309个采样点的SOC进行了福建省复杂地形区的适宜性研究，结果发现简单克里金对复杂地形、丘陵山区和河谷盆地地区插值效果好，反距离权重适用于平原平台地区.马利芳等[12]运用普通克里金、反距离权重、径向基函数和局部多项式法预测了不同人为干扰程度下干旱区土壤有机质的空间分布，结果表明普通克里金在无人为干扰的地区效果最好，而径向基函数在重度人为干扰区效果最好.

从以上研究可以看出，各插值法在不同区域的适用性有很大差异[8-13]；其次，这些研究大多局限在单一时间尺度下，较少考虑不同时期土壤属性差异对插值精度的影响；最后，地表条件和人为活动的差异将导致SOC产生明显的时空变异，影响最优插值模型的筛选[14].因此，为了准确估计SOC含量，基于样点的适宜插值方法选择时必须要考虑空间和时间维度.基于此，本研究以我国太湖地区23 200 km2水田土壤为研究对象，利用1982年第2次土壤普查和2000年土壤质量演变与持续利用“973”项目的实测样点数据，分析目前土壤学常用的11种插值方法对不同时期水田SOC预测精度影响，筛选出整个地区、不同水稻土亚类和行政辖区的最优插值模型，旨在揭示土壤属性变异对最优插值模型影响的内在机理，为我国南方水田SOC时空演变下的最优插值模型筛选和合理制定碳汇动态管理措施提供理论依据.

1 材料与方法

1.1 研究区概况

太湖地区(118°50′—121°54′E，29°56′—32°16′N)位于长江三角洲南缘，属于亚热带季风气候，气候温和，水热条件优越；年太阳辐射量高达4 686 MJ·m-2，年均气温15～17 ℃，年均降水量1 177 mm，农田管理主要为水稻和冬小麦轮作制度，是中国传统粮食高产区[5].该地区总面积约36 900 km2，其中66%被水稻土覆盖[15].

本研究区分属两省一市，包括浙江省、江苏省和上海市3个辖区，共覆盖37个县(市、区).根据成土母质、土地利用方式、耕作制度和农业利用分为4个主要土区(图1a)，分别为以湖(河、海)相沉积物、长江冲积物形成的太湖平原土区(面积占比17%)、冲积平原土区(面积占比26%)、各种岩石残坡积物及下蜀黄土形成的丘陵低山土区(面积占比31%)和沼泽土形成的低洼圩田土区(面积占比27%)，并逐渐发育为潴育、渗育、脱潜、漂洗、淹育和潜育水稻土等6个水田土壤亚类[16](图1b).本研究选取太湖地区水田土壤面积最大的3个主要亚类作为研究对象，分别为潴育水稻土、脱潜水稻土和渗育水稻土，面积占比分别53%、18%和16%.

1.2 数据来源

1982年土壤属性数据来自浙江省、江苏省和上海市第2次土壤普查的各县(市、区)土壤志，共计1 096个水田土壤剖面样点；2000年土壤属性数据来自中国科学院南京土壤研究所主持的“973土壤质量研究”项目，共计1 370个水田土壤表层样点.根据Bemmelen转换系数计算得到SOC含量后，为保证历史数据的真实性和最大限度被利用，通过5S法(均值加减五倍标准差)剔除异常值，当异常值比总体均值大(小)5倍标准差以上(下)且比近邻8个样点均值大(小)3倍标准差以上(下)时，使用该规则下的最大最小值代替[17].此外，基于ArcGIS地统计分析Create Subset模块按照4∶1的比例将两期样点集随机分成预测集与验证集，得到太湖整个地区1982年预测集样点共877个，验证集219个，2000年预测集样点共1 096个，验证集274个(图2)[18].

1.3 数据探索与空间插值模型拟合

基于ArcGIS 10.2 Geostatistacal Analyst模块下常用的7种确定性插值方法[反距离权重(inverse distance weighting、IDW)、全局多项式(global polynomial interpolation、GPI)、局部多项式(local polynomial interpolation、LPI)、规则样条函数(completely regularized spline、CRS)、张力样条函数(spline with tension、SWT)、高次曲面函数(multiquadric function、MF)、反高次曲面函数(inverse multiquadric function、IMS)]，以及4种地统计方法[普通克里金(ordinary Kriging、OK)、简单克里金(simple Kriging、SK)、泛克里金(universal Kriging、UK)和析取克里金(disjunctive Kriging、DK)]进行插值[18].IDW是基于相近相似原理，以插值点与样本点之间的距离为权重进行加权平均的精确插值方法；GPI和LPI是分别利用1个低阶和多个的多项式进行拟合的不精确插值方法；同属于径向基函数的CRS、SWT、MF、IMS，基本原理是经过每一个已知观测点、形成总曲率最小的橡胶薄膜状预测表面，而不同的方法则对应膜拟合点集的不同方式[18].地统计的OK、SK、UK和DK是以变异函数理论和结构分析为基础，在有限区域内对区域化变量进行无偏最优估计，不同方法对应点集适用的条件不同[19].

为满足地统计插值方法正态分布的前提与平稳性理论假设，在SPSS、ArcGIS和GS+9.0中进行正态检验及空间自相关分析[18-21].由于本研究各分类预测集均为超过100的大样本，利用效果较理想的偏度峰度值联合K-S检验对各预测集进行正态分布性检验，若K-S方法中Z值的相伴概率值大于当前显著性水平，认为样本来自的总体与指定正态分布无显著差异；否则需进行转换.其次，由于土壤样品采样点离散分布会掩盖空间分布相关性，需要进行离散度与相关性分析以避免出现纯块金效应，造成克里金插值估值仅为简单的数学平均值[19].全局莫兰I指数可验证区域整体空间模式和样本空间自相关性，指数I=0表示随机分布，I>0表示存在空间正相关，且关系显著时表示变量存在明显空间聚集现象，数值越大关系越密切，性质越相似；I<0表示空间异常，数值绝对值越大说明差异越大越分散[20-21].最后，在GS+9.0模拟得到半变异方差拟合结果[18-19].半变异拟合模型参数平方残差和RSS越小越好，模型决定系数R2越大越好，且优先考虑RSS.

1.4 预测结果精度检验

通过预测集数据估测自相关模型的交叉验证方法确定某一种插值方法的最优参数设置；然后通过外部验证对最优参数设置的不同插值模型进行精度评价，基于“平均预测误差(ME)越趋近于0、均方根误差(RMSE)越小且优先考虑后者”的原则，得到1982年和2000年太湖地区水田SOC最适宜插值方法[7,18,22].

(1)

(2)

(3)

式中，N为采样点数量，Xoi为采样点SOC含量实测值，Xpi为采样点SOC含量预测值，R为实测值和预测值之间的Pearson相关系数，其越大表明模型对各样点集含量的解释能力越强.

2 结果与分析

2.1 太湖地区水田SOC样点基本统计特征

由表1可得，1982年和2000年太湖水田SOC含量(0～20 cm)范围分别在1.91～37.39和1.91～44.59 g·kg-1之间，均值为(15.95±5.32)和(18.50±5.31) g·kg-1.从变异系数来看，两个时期太湖水田SOC含量的离散程度相差不大，均在10%～100%之间，为中等变异[23].从整个太湖地区和不同水稻土亚类、行政辖区各预测集样点SOC的偏度、峰度和K-S检验值来看，1982年和2000年研究区各预测集均符合正态分布，全局莫兰I指数的范围为0.146～0.448，对应Z得分范围是6.45～35.43，Z高于2.58且显著性均小于0.01，表明两期预测集的SOC含量有明显的空间聚集现象，具有空间正相关模式，符合地统计学插值前提[21].

表1 太湖地区水田SOC含量描述性统计特征1)

第2次土壤普查以来，太湖地区整个区域水田SOC的含量平均升高了2.55 g·kg-1，这与Liu et al[22]分析的1982—2000年太湖地区水稻土SOC含量呈上升趋势的结果一致.太湖地区水稻土SOC含量上升的主要驱动因素是肥料的大量施用和降雨量的明显增加.据统计，1982年太湖地区农家肥和氮肥的平均施用量分别为231和243 kg·hm-2，而2000年为270和345 kg·hm-2，增幅分别达到19.86%和37.66%[24].其次，气候因子也在太湖地区水田SOC提升中起着重要作用.据统计，该地区的年均降雨量由1982年的1 102 mm提高到2000年的1 175 mm，降雨量的增加有利于SOC积累[24].进一步统计表明，1982—2000年间整个地区水田SOC的变异系数增幅为-13.89%，而3个主要亚类和3个行政辖区变异系数增幅有正有负(潴育、渗育和脱潜水稻土分别为-13.56%、-4.15%和2.69%，江苏、上海和浙江分别为-27.90%、-23.74%和7.26%)，可见过去19年间太湖地区水稻土SOC整体空间变异性变化缓和，但局域变异变化差异较大，这与第2次普查时期统一经营转变为家庭联产承包责任制后的农田管理方式有关[14].

2.2 太湖地区水田SOC半变异拟合

1982年和2000年太湖地区水田SOC半变异函数模型决定系数R2均高于0.824(表2)，残差平方和RSS均低于0.375，说明半变异拟合效果能够充分反映各指标的空间结构特征.同时，半变异模型符合常见的指数、高斯和球状模型，其中指数模型更适用于SOC含量拟合[18-19].

由表2可得，太湖整个水田SOC的块金值(C0)在1982年为0.015，2000年为0.002，均小于对应年份各土壤亚类和各行政辖区的C0，且C0越大RSS误差越大，说明SOC的C0与空间尺度为负相关，与空间分布随机性为正相关[25].基底效应范围为2.44%～51.81%，表示太湖地区SOC具有中强空间自相关性，同时受到施肥、耕作、种植制度等人为随机因素和母质、土壤类型、气候、地形等结构性因素影响.基底效应值越大说明空间自相关性越被削弱，空间变异越受到随机效应的影响[26-27].同时有研究证明，在人为因素影响下土壤属性变异表现出强烈的随机性，其结构性和相关性被削弱，空间分布将朝均一化方向发展[10,28].

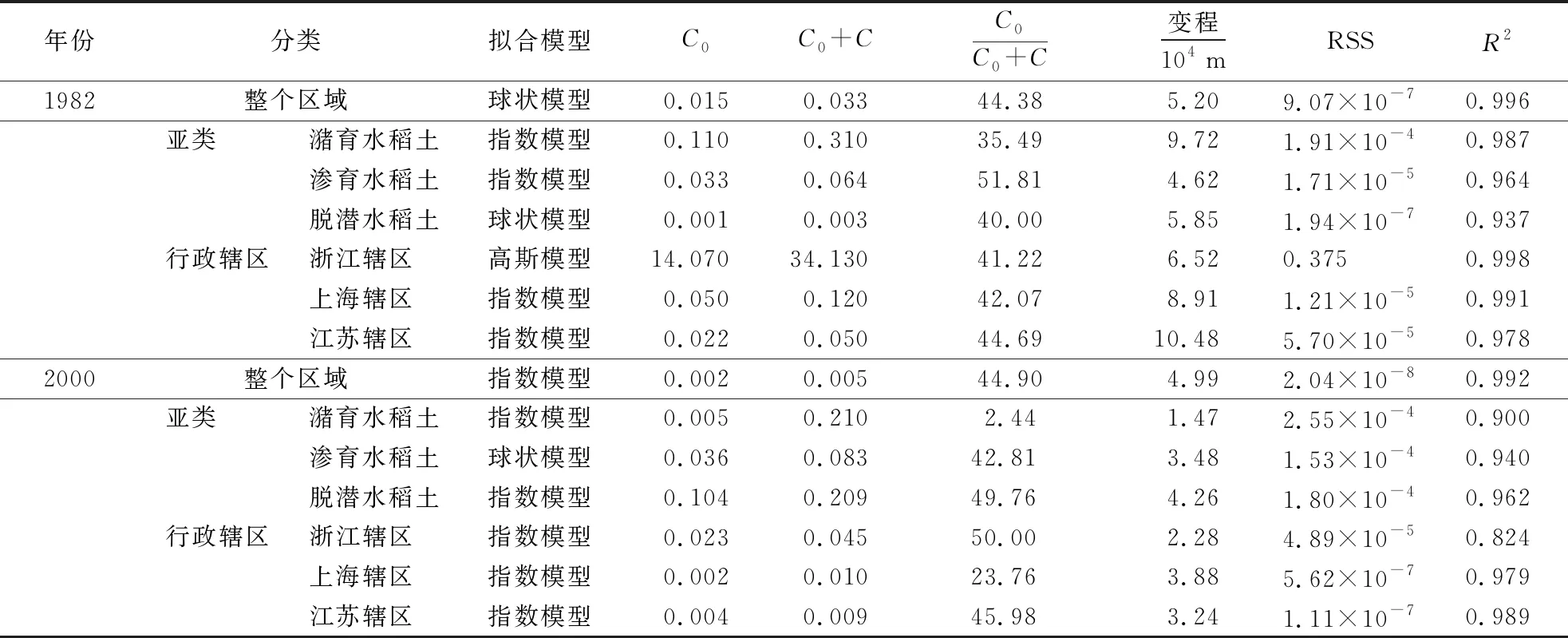
表2 两期太湖区域不同土壤亚类和行政辖区水田SOC半方差模型1)

从变程变化来看，2000年太湖地区各水稻土亚类比1982年减少1.14×104～8.25×104m，行政辖区减少4.24×104～7.24×104m，而整个区域仅减少0.21×104m，表明过去19年间随着SOC的积累，不同水稻土亚类和行政辖区的局部空间变异缓和，但对整个区域自相关范围影响不大.

2.3 整个地区水田SOC的最优插值方法

由图3可得，1982年太湖整个地区不同插值方法下SOC的分布图较为相似，总体上SOC含量均表现为中部和西南部区域含量较高，西北部、东南部和北部沿江区域含量较低，其他地区含量为中等水平；绝大部分地区处于12～14 g·kg-1及以上含量.随着时间变换，2000年各对应插值方法的SOC空间分布格局与1982年相似，但极值差异缩小，高值区域分布增多，绝大部分地区处于14～16 g·kg-1及以上含量.从插值效果来看，7种确定性插值方法SOC分布差异很大，而4种地统计插值方法空间分布相似性高.其中，LPI和GPI呈现明显的阶梯状变化，形成高值区到低值区的缓冲带，GPI的空间分布图在研究区西北边角发生了扭曲变形.同属于径向基函数系列的IMS、MF、SWT和CRS大区域空间分布相似，但在小区域不同方法表现出不同程度的高低波动.IDW插值的空间分布图像表面不平滑，“牛眼”现象严重.地统计插值OK、SK、UK和DK的空间分布连续且表面平滑，但局部的插值结果有明显不同.

从不同确定性插值方法的精度评价来看(表3)，1982年和2000年太湖地区水田SOC均是IDW精度最高，而MF的预测值与实测值差异最大，说明IDW能较好地模拟研究区SOC的空间变异.进一步从插值函数适用性来看，由于1982年和2000年整个太湖地区SOC含量极值分别高达35.48和42.58 g·kg-1，基于人工神经网络的MF允许模拟值超出实测极值，短距离邻域的SOC出现剧烈变异时易产生较高均值误差，从而降低预测精度；但基于相近相似原理的IDW则是周围实测点数量越多、距离越近，预测点位越受影响、值越相似，因此预测值更符合太湖地区SOC含量值[29].张海平等[30]在评估IDW和径向基函数适用性时也认为在预测极值与采样点一致的应用中IDW效果更好，这与本研究的结果相一致.

从不同地统计插值方法的精度评价来看(表3)，1982年太湖地区水田SOC最优地统计方法为OK，2000年为DK.进一步从插值函数适用性来看，由于太湖地区总体地势平坦，冲积平原和太湖平原占研究区总面积的55.17%，OK能较好地预测平坦地区SOC的细部变异.Addis et al[9]同样认为最优无偏估值的OK对农业流域塔纳盆地的SOC拟合效果最好.然而，与1982年相比，2000年太湖地区水稻土SOC的预测集样点增加19.98%，而基于非线性连续型数据转化的DK可充分利用大量样点详尽信息，能给出基于现有信息更精确的SOC概率分布估计值. Li et al[7]的研究也表明在低样点密度下DK可能增加预测面平滑度从而显著高估或低估预测误差，而高密度的采样有利于提高SOC的预测精度.

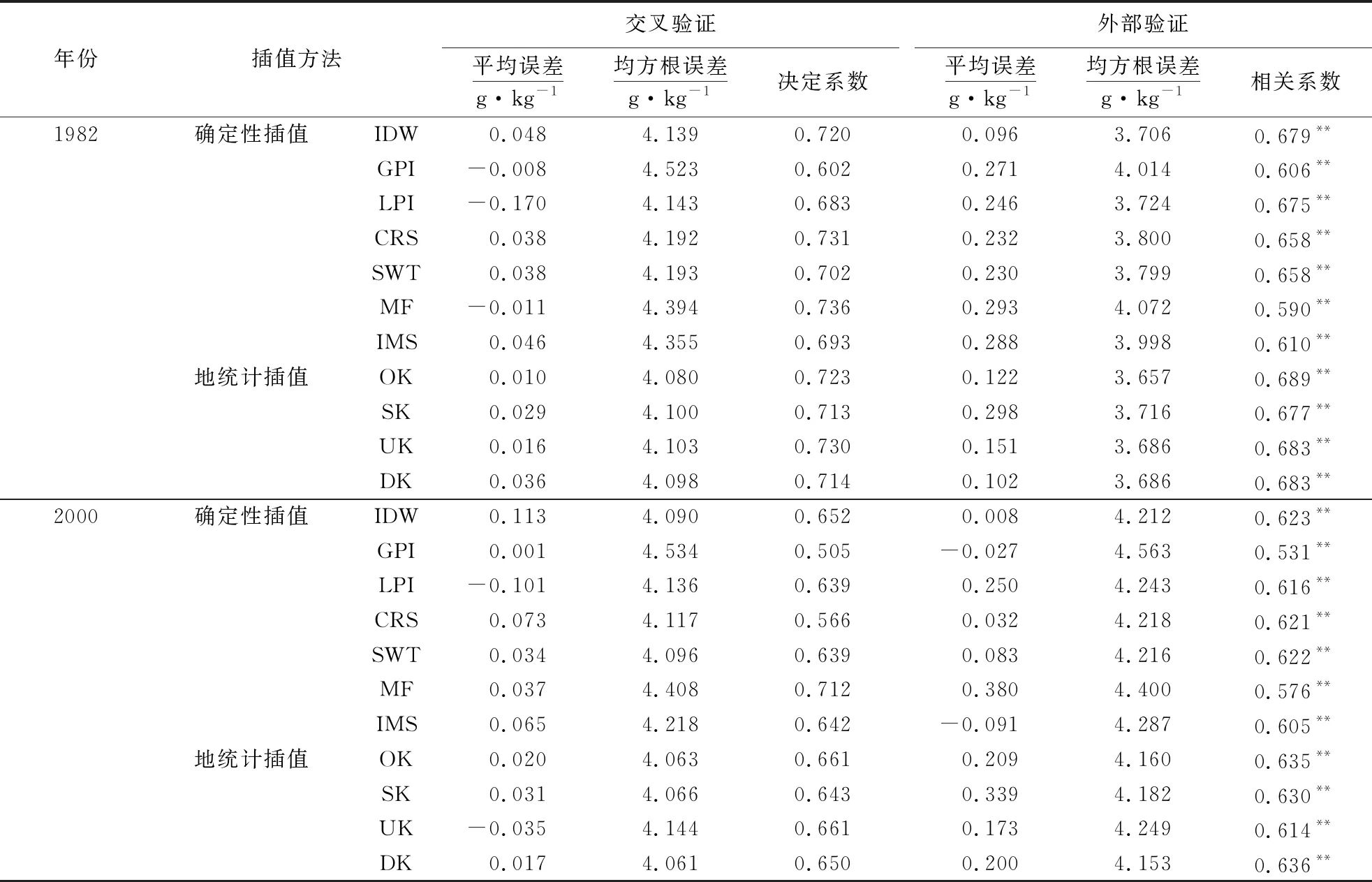
表3 太湖地区水田土壤整个区域插值模型预测精度评价1)

总体来看，1982年和2000年太湖地区水田SOC最优插值方法分别是OK和DK.两期中，地统计插值均为最优的主要原因在于，此方法不仅考虑了SOC预测点位与实测点的距离，而且兼顾了SOC空间分布与空间方位关系，适用于预测结构性与随机性并存的连续变量[25].同样，在空间插值方法在不同领域适用性研究中，李海涛等[29]也提出克里金插值算法可适用于土壤样本数据存在随机性和结构性特征的场景.从整个太湖地区水田SOC含量变异来看，2000年的自相关程度和随机因素影响程度比1982年有所提高，表现在2000年基底效应升高0.52%并且块金值降低6.64倍，说明除植被、地形、气候和母质等自然因素影响外，长期施肥等随机人为因素引起的变异导致两期最优插值方法发生变化[24,26,28].

2.4 不同时期各水田土壤亚类SOC的最优插值方法

对于面积占整个太湖地区水田53%的潴育水稻土SOC来说，1982年最优插值方法为确定性插值的LPI，而2000年为地统计插值的SK(表4和表5).1982年77.06 %的样点密集分布在低洼圩区和冲积平原土区交界处，SOC变异系数高达30.17%，而全局莫兰I指数仅0.207，该时期的潴育水稻土与相邻近区域SOC含量相似程度低且局部变异明显，LPI可捕捉数据集的短程变异，因此更为适用[8].2000年太湖地区潴育水稻土的采样点在各土区分布均匀，全局莫兰I指数提高了0.127，变程则在各亚类中减少最多(8.25×104m) (表2)，尽管确定性插值IDW对自相关性密切且邻值近似的SOC插值效果较好，但1982—2000年期间由于较高年降水量(1 219 mm)、年均温度(16.6 ℃)和大量秸秆还田等因素的长期影响，潴育水稻土SOC的变异系数、块金值和基底效应比1982年分别降低了4.09%、95.36%和33.05%；在这种情况下，兼顾平稳性和空间关系的SK更适用于该亚类SOC的预测[6,24].史舟等[19]也认为线性SK比OK在二阶平稳的随机过程中预测精度高，而长期人为影响造成水田SOC趋向均一，因此有利于提高简单克里金的预测精度[28].

渗育水稻土占整个太湖地区水稻土总面积的16%，1982年和2000年该亚类SOC含量的最优预测插值方法均为确定性插值，分别是GPI和LPI(表4和表5).这是因为1982年该亚类分布均匀，同时全局莫兰I指数在所有土壤亚类中最高，表明该时期渗育水稻土SOC受局部影响弱且临近区域相似度高，而GPI可忽略局部异常值而对整个预测表面进行整体平滑，较适用于分布范围广而属性变化缓慢的样点预测[26].但2000年渗育水稻土55.87%的采样点分布在太湖地区北部冲积平原土区，SOC含量邻域相似度弱且多局域存在较大差异，此时局部插值的LPI更适用；此外，1982—2000年间随着经济的发展和农业投入的增加，渗育水稻土亚类的化肥和有机肥年均施用量分别达到324和240 kg·hm-2，较高的肥料施用量一方面会使该亚类SOC含量升高，另一方面也会导致不同微地貌下SOC的空间变异增大，在这种情况下，LPI较其他插值方法能更准确地预测SOC含量[24,31].Bogunovic et al[32]对人为干扰强烈的农村森林交界区土壤有机质预测时也得到LPI是优于IDW、OK、SK的最好插值方法，该研究中基底效应高达59.56%，但变程仅是采样间隔的8.64倍，一定程度上也证明了LPI适用于随机干扰大、短距离自相关性强且空间属性变异剧烈的农耕区.

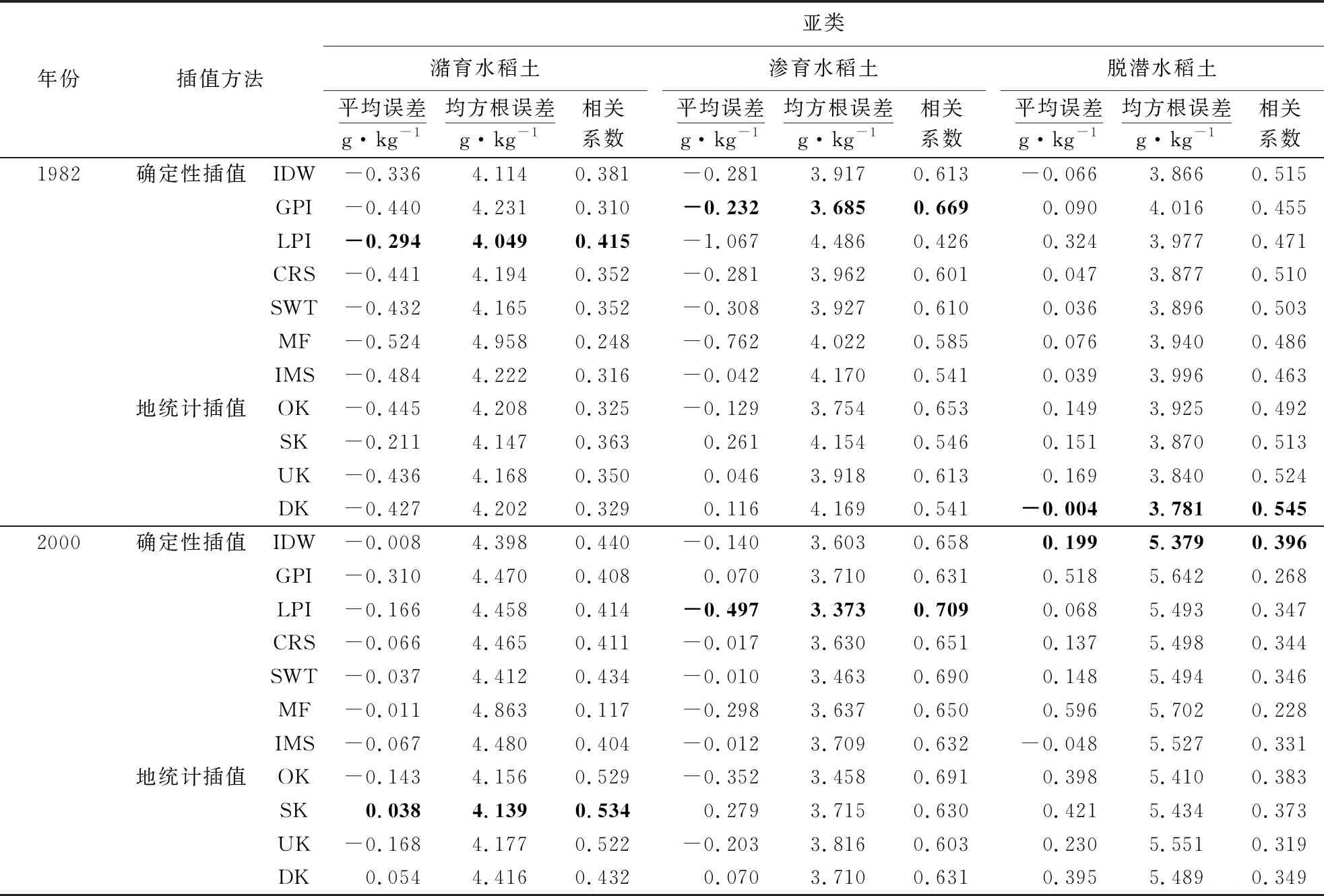
表4 两期太湖地区水田土壤主要亚类SOC含量预测误差1)

表5 两期太湖地区整个区域和主要亚类最优插值方法预测精度对比

脱潜水稻土占整个太湖地区水稻土总面积的18%，介于潴育和渗育水稻土之间.1982年和2000年该亚类SOC最优预测插值方法分别为地统计的DK和确定性插值的IDW(表4和表5).这主要是因为1982年渗育水稻土在所有亚类中基台值最高，高比例随机影响下，变程内的相邻样点之间可能无法满足非简单相关关系；在这种情况下非线性插值DK可根据概率分布估计SOC含量，提高预测精度[7].2000年研究区脱潜水稻土55.46%样点分布在低洼圩区、33.61%分布在太湖平原与冲积平原土区，基底效应和全局莫兰I指数大而变程小，对于样点自相关性密切且邻值近似、局部属性弱波动的SOC，IDW预测精度较高.Long et al也证明在预测地势平缓的平原台地区SOC时，IDW的精度要高于地统计插值方法[11].

总体来看，1982年和2000年太湖地区潴育、渗育、脱潜3个主要水稻土亚类的SOC含量最优空间预测方法随着时间的推移发生了明显变化，并且与整个太湖地区最优方法不一致，这可能是因为亚类在不同时期的施肥量和气候差异导致土壤属性变异程度不同，进而使得适宜的插值模型产生了改变.

2.5 不同时期各行政区水田SOC的最优插值方法

太湖地区浙江辖区水田1982年和2000年的SOC最优插值方法分别为SK和CRS(表6和表7).这主要是因为1982年56.50%的采样点位于低洼圩土区(海拔低于4 m)，其余样点位于低山丘陵土区和冲积平原土区(海拔4.5～7.0 m)，邻域地势多变且SOC含量空间差异大；SK在SOC空间预测中易忽略细部极值影响而产生平缓预测面，适用于地形复杂区[11].2000年太湖地区浙江辖区50%的采样点集中于平原区域，低山丘陵土区的样点大幅减少，再加上大量施肥等随机因素影响，基底效应升高8.78%，变程降低42 400 m；而CRS作为局部收敛的精确性插值器，更适用于样点聚集度极高、局部变异大的SOC预测[31].有研究表明，与克里金和IDW模型相比，径向基函数模型可以更真实地反映分析空间变量的结构[11].

表6 两期太湖地区水田土壤行政辖区SOC含量预测误差1)

表7 两期太湖地区整个区域和行政辖区最优插值方法预测精度对比

上海辖区水田1982年和2000年SOC最优插值方法分别为OK和SK(表6和表7).这主要是因为1982年该地区59.05%样点分布在东北部平原土区，其余分布于西南低洼圩区，区域内极值适中，OK对于地势平坦的县域土壤属性插值效果更好.龙军等[18]也认为OK方法可以较好预测平原县域耕地SOC.但在2000年，属于上海辖区的冲积平原土区采样点比例比1982年提高了5.31%，尤其城市扩张造成崇明岛和上海市区耕地大量减少形成更大范围无样点分布的空白区，SK可利用经验模型平滑预测面进行非平稳结构的线性预测，尤其适用于这类微地形等结构性因素影响更多的情况.

江苏辖区水田1982年和2000年SOC最优插值方法均为OK(表6和表7).该辖区两期样点平原区的占比较高，分别达50.98%和56.77%.在不同确定性方法中，1982年江苏辖区水田SOC的全局莫兰I指数在各行政辖区中最高达到0.433，表明空间邻域上SOC相似度高，但同时潴育和脱潜水稻土SOC含量极值差异大造成区域内部变异大，CRS可通过最小化表面曲率对平原区为主的区域实现较高精度的预测，因此为1982年最优确定性插值方法[18].2000年，一方面江苏辖区潴育水稻土样点比例增加到了60.23%，另一方面SOC含量处于中高水平的潴育水稻土和脱潜水稻土一般分布于该辖区中部，而SOC含量处于低水平的渗育水稻土分布于该辖区边缘部分；LPI在区域特征值聚集明显情况下的预测精度较高，因此该方法在2000年确定性插值中最优.OK在弱化细节变异、有效地避免边缘效应上优于所有确定性插值方法，因此江苏辖区水稻土两时期SOC含量的最优预测方法为OK[7].

总的来看，1982年和2000年江苏、上海、浙江辖区水田SOC含量的预测地统计学方法的插值精度最高，适用性最好.很多研究也发现，地统计方法尤其是OK在SOC含量数字制图中能够平滑极值保证预测精度，同时也可展示较完善的细部变异情况[9-10].从时间变换来看，浙江辖区的水田SOC含量受1982年和2000年间样点分布土区、施肥情况等因素影响，最优预测方法从确定性插值转变为地统计学插值，而上海和江苏辖区两期最优预测插值方法皆为地统计，原因可能与水稻土亚类属性等结构性因素和耕作方式等随机因素影响相似有关.从空间变换来看，两期均方误差排序整体均为浙江>上海>江苏，插值精度与3个行政辖区的块金值趋势一致，说明行政辖区水田SOC插值误差受微观效应引起的空间变异显著[16].

3 讨论

明确SOC最优插值方法的时空变化对动态制定我国农田SOC“碳汇”管理政策具有重要意义.本研究结果表明，1982年和2000年整个太湖地区水田SOC最优插值方法分别为OK和DK，这前人研究得到的地统计方法中的OK为农业流域SOC预测的最佳插值方法[9]和高密度采样时DK适用性更高[7]的结论一致.从不同亚类来看，1982年和2000年各个水稻土亚类LPI、GPI和IDW 3种确定性插值的SOC预测精度高于常用的OK、SK、UK和DK 4种地统计方法.较少学者讨论过不同亚类土壤属性插值方法的适用性，但在基于亚类的插值预测效果上，Biswas et al[33]提出按土壤类型布设样点进行数字土壤制图的合理性，张忠启[13]也认为土壤亚类样点可以更详尽地反映SOC地形地貌地方性特点的空间变异，从侧面证明了本研究基于土壤亚类的插值预测可以充分反应SOC含量的空间变异特征.另外，本研究的结果表明各土壤亚类的SOC最优预测方法除了受不同土壤分区微地形因素影响外，长期不同农业管理方式也会造成SOC含量变异程度的差异，从而改变其最优插值方法.对于此，马利芳等[12]的研究同样表明人类干扰强度大的地带，确定性插值优于地统计插值精度，与本研究结果一致.从不同行政辖区来看，1982年和2000年大部分地区的最优插值方法是地统计，其中OK适用性比SK、CRS等插值方法更广.同样，学者们在县域行政区进行土壤属性空间分布预测时，结果也表明OK在较为平坦的行政区内预测面平滑且插值效果较好[8,10].

总之，SOC最优插值方法的选择与结构性、随机性不均衡影响下的时空变异有关，建议在进行SOC空间特征、定量预测和适宜样点数研究时，应充分考虑样点分布、人为活动和环境因素等造成时空变异的影响因子.随着时间变化应关注最适宜插值方法的变化，且在土壤亚类插值研究时应考虑确定性方法的使用，这样更有利于精准选择适宜插值方法进行空间预测和定量分析.

尽管本研究基于1982年和2000年两期大样点实测数据，从行政辖区和土壤亚类的样点分布、插值原理、土区、气象及人为因素等多方面分析了太湖地区水稻土SOC最优插值方法时空变化的机理，但SOC最优插值方法也受到其他土壤属性，如成土母质和碱解氮等的影响，有待于进一步研究.