基于临界面的多轴振动疲劳寿命预测

裴晨晖，何欢，陈国平

（南京航空航天大学 a. 机械结构力学及控制国家重点实验室；b. 振动工程研究所，南京 210016）

在实际工程应用中，结构往往受到多轴振动载荷的影响，造成疲劳损伤，进而导致结构的失效破坏。相比单轴疲劳，多轴疲劳在疲劳损伤上会有附加强化效应，这主要是受材料自身特性与加载路径的影响。通常来讲，多轴疲劳是多轴载荷作用下的疲劳问题，指多个非比例的、不同频率的载荷相互独立地作用在工程结构上，从而引起结构的疲劳破坏。而对于相同频率、相位的比例载荷，通常作为单轴疲劳问题进行处理。

振动疲劳中的主要处理方法为时域分析法与频域分析法。时域分析法主要运用进行雨流计数法，将随机的振动载荷分解为不同的循环。频域分析中，输入与输出都通过不同频率的能量显示，功率谱密度（PSD）是表示振动环境中频率载荷与响应最常用的方法，窄带分析、Dirlik 经验公式是常见的频率内评估寿命的方法。

多轴振动疲劳理论有三类[1]：等效应变法、能量法、临界面法。等效应变法最著名的是Manson-Coffin公式[2]。能量法[3]最先由Morrow 提出，其将金属疲劳产生的原因归结为：每一次载荷循环中，材料吸收了外部能量而产生了不可逆的损伤，这种塑性功的累积最终导致了材料的破坏。临界法则在考虑应力、应变的基础上，还考虑了应力、应变所在平面的影响。与等效法相比，临界法更加符合疲劳裂纹的产生和扩展机理，因此，被广泛认为是分析多轴疲劳的有效方法。临界法中有基于最大切应变准则的KBW 模型[4]、Shang-Wang 模型与FS 模型[5]等。临界法通常选择一个确定的平面作为临界面，利用临界面上的应力状态（包括正应力与切应力）计算得到等效应力，计算疲劳寿命[6-8]。

笔者通过一种新的以主应力为基础的临界法对多轴疲劳问题进行分析，将不同时刻下的主应力投影到某一主应力平面内，得到该平面内的应力-时间曲线，进而分析单个循环内该平面方向上的疲劳损伤，即先进行疲劳损伤的计算，再确定临界面与预测寿命。通过对不同平面方向进行加权平均，最后求得疲劳临界面的期望方向与预估寿命。并通过薄片试件的多轴加速度随机振动疲劳试验，验证该方法的准确性。

1 理论分析

1.1 临界法

临界法[9]的关键问题在于确定临界面，确定临界面的方法有很多种，因此形成了不同的临界面疲劳模型。常规的有适用于低周疲劳的最大切应力准则，和适用于高周疲劳的主应变或应力准则。从各类多轴高周疲劳的试验结果来看，疲劳破坏确实与最大主应力或应变有很大的关系。通过引入权函数的方法确定临界面已经成为了确立临界面的常规方法[10]。在平面问题中，假定临界面的期望值为ˆθ ，则：

式中：Di为一次循环的损伤值；Dmax为各主应力平面下损伤的最大值； c 为常量参数。

1.2 非比例附加强化

多轴载荷的影响主要体现为正应力与切应力的应力比以及两者的相位差所带来的非比例附加强化效应。不同的非比例载荷会使得材料危险点处的应力应变主轴发生旋转，从而导致材料的抗疲劳性能降低。Chen 等[11-13]定义了一个能表示非比例加载路径变化对多轴疲劳性能影响的非比例路径因子Φ 。在此基础上，一种新的多轴临界面预测模型[14-15]，在考虑非比例加载条件下路径与材料非比例强化特征的疲劳性能影响后，引入了一个非比例影响因子k：

式中：Φ 为非比例路径因子； L 为材料非比例附加强化参数。笔者沿用该因子，在高周疲劳问题中，其应变比、应变相位差对应转变为应力比、应力相位差。

1.3 多轴线性疲劳累积理论

疲劳损伤累积理论中[16-17]，Miner 理论作为经典的线性累积模型，被广泛地运用于多轴疲劳领域。线性累积损伤理论中的疲劳损伤按线性累加，各个载荷之间互相独立。在平面问题中，线性累积损伤理论首先使用临界法计算危险点-90°至90°各方向的多轴等效应力 σ (θ )，然后通过各方向上的多轴等效应力σ (θ )，使用多轴疲劳寿命分析方法计算相应的寿命Nf，再分别使用Miner 理论进行损伤计算。Miner 理论将多轴下一个循环造成的损伤定义为：

2 确定临界面

临界面法的通常做法是先确定临界面，再利用临界面上的应力状态求解等效应力，预测寿命。对于临界面的确定，笔者采用将一段时域范围内的正应力投影计算损伤后加权平均的方法得到。具体流程如下：

1）利用矩阵法求解不同时刻的主应力方向与主应力大小；

2）取特定的平面，将各个主应力投影，得到该平面下主应力的时域变化曲线；

3）利用雨流计数法，结合S-N曲线与非比例附加强化因子计算求解平面下的疲劳损伤；

4）求解不同平面下的疲劳损伤，利用权函数得到临界面的期望值；

5）利用疲劳损伤累积理论计算寿命。

3 仿真分析

3.1 试件概况

建立如图1 所示的试验件有限元模型，主体材料为LY12-CZ[19]，弹性模量68 GPa，泊松比0.33，密度2.8 g/cm3；质量块材料为Q 235，质量0.156 kg。

图1 结构有限元模型Fig.1 Structural finite element model

将底端（矩形部分）固支，计算得到结构的垂向一弯的频率为 13.067 Hz ， 侧向一弯的频率为42.885 Hz，一扭的模态频率为90.434 Hz。

3.2 随机振动响应分析

试验件底端（矩形部分）上利用施加Z向、X向的随机加速度激励。激励为0.006g2/Hz、频率范围10～200 Hz 的平直谱。对有限元模型进行随机响应分析，得到危险点的位置（弧形部分根部），以及其应力的随机响应。危险点主要为Y向正应力与XY向切应力，两者PSD 曲线如图2—5 所示，并用三角级数法生成时域应力响应。在试验过程中，可以得到应变-时间曲线，从而得到观测时间内应力状态的时域变化曲线。此处，以PSD 曲线生成的时间-应力曲线计算临界面的期望值。

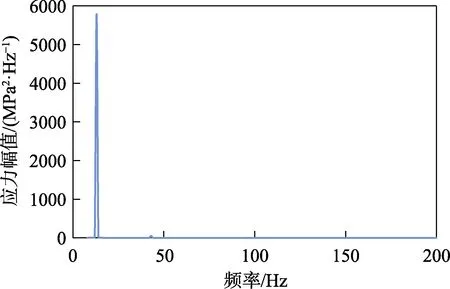
图2 Y 向正应力频域响应Fig.2 Frequency domain response of normal stress in Y direction

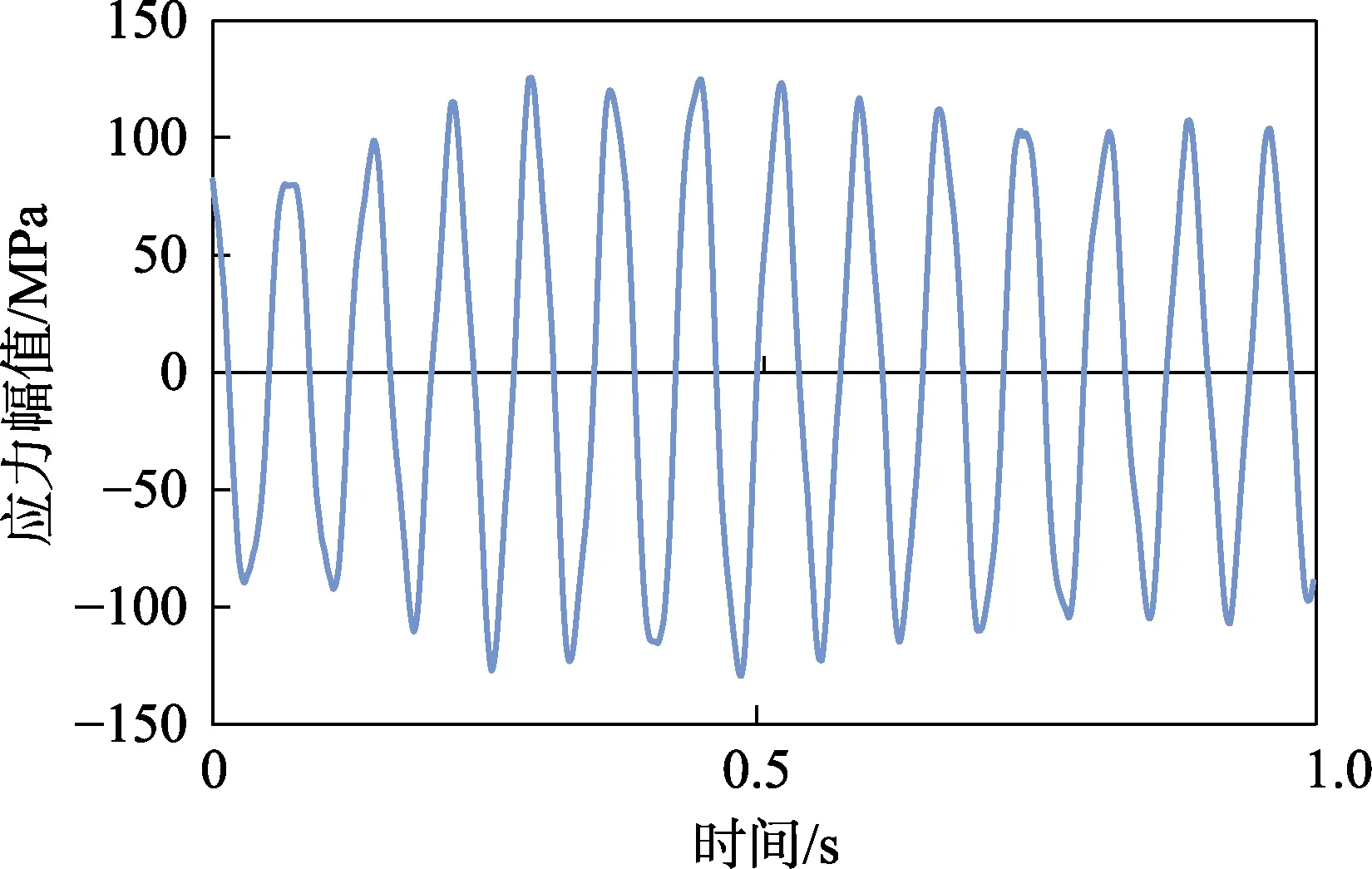
图3 Y 向正应力时域响应Fig.3 Time domain response of normal stress in Y direction

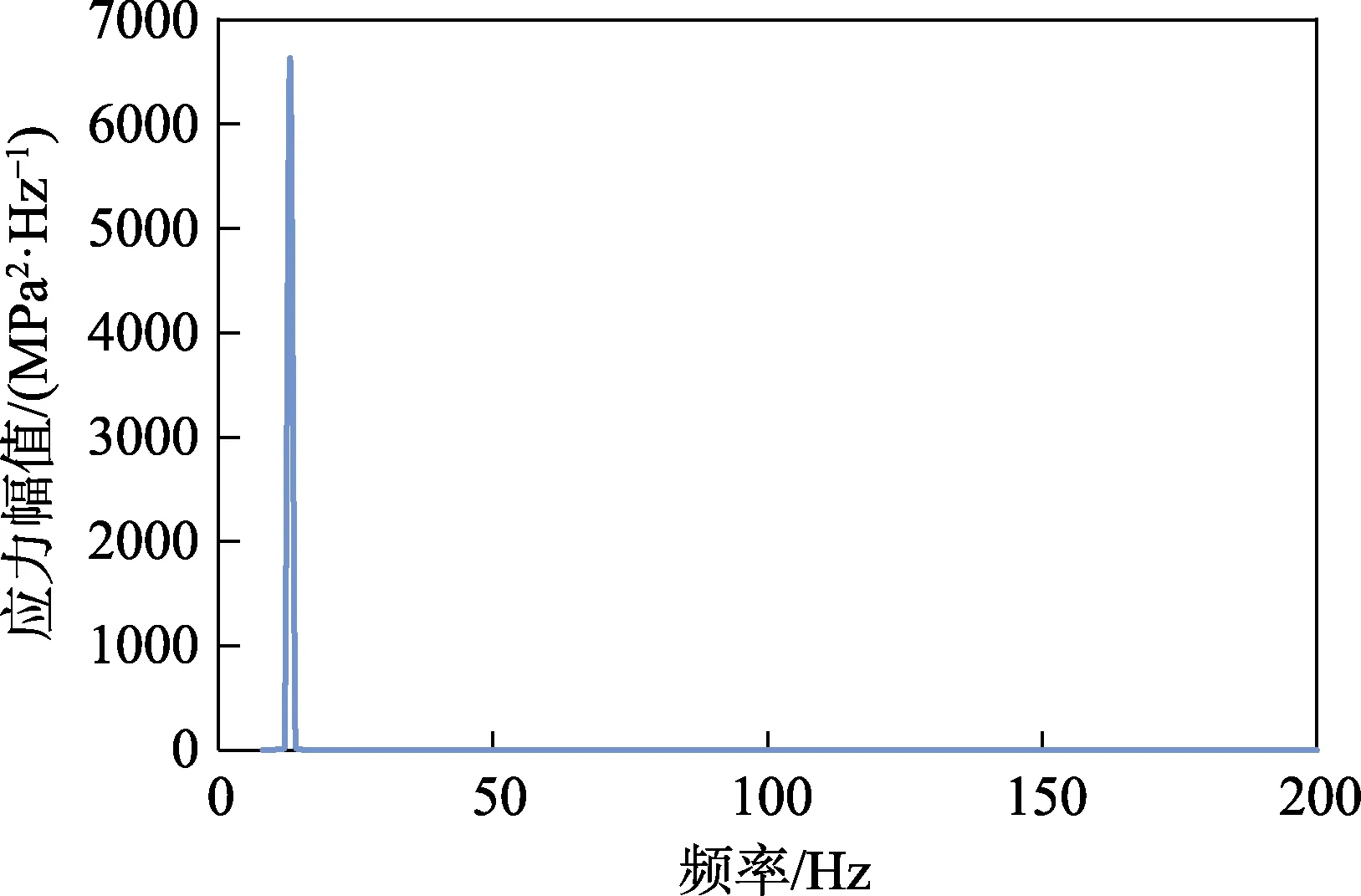
图4 XY 向切应力频域响应Fig.4 Frequency domain response of shear stress in XY direction

图5 XY 向切应力时域响应Fig.5 Time domain response of shear stress in XY direction

对时域部分的应力响应进行傅里叶变换，得到X向正应力、XY向切应力的频域分析结果，可知正应力在13 Hz 时最大，为72 MPa；XY切应力在13 Hz时幅值最大，为145 MPa。取非比例路径因子Φ为0.5，计算如图6 所示。c取0.8，计算得到临界面的方向为71.8°，线性差值得到疲劳损伤为3.007×10-5，预估寿命9 978 s。

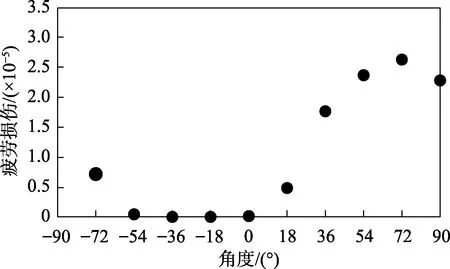
图6 各个方向上的疲劳损伤Fig.6 Fatigue damage in given directions

3.3 随机振动寿命预测

文献[20]进行了4 种工况下的疲劳试验，利用第2 章的临界法理论计算寿命预测结果，并与试验结果进行对比，得到预测寿命结果与实际结果的基本误差在两倍界以内。

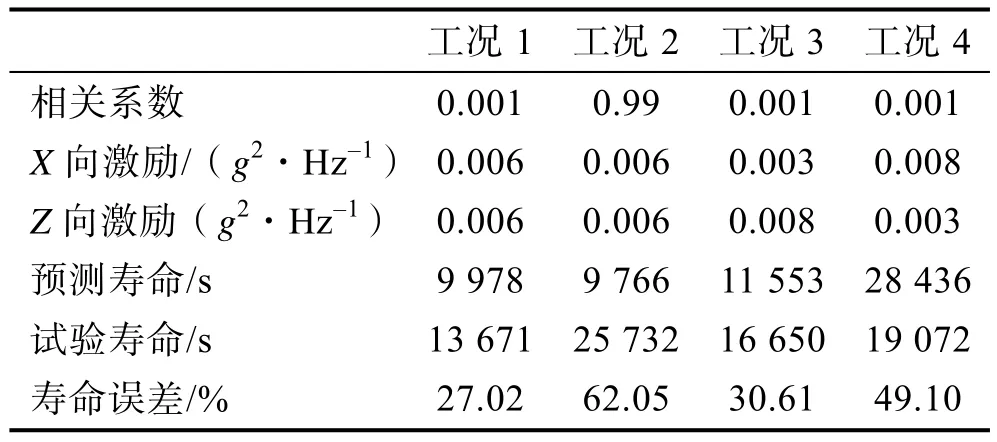
表1 多轴振动试验工况与寿命预测Tab.1 Multi-axis vibration test conditions and life prediction

4 结论

1）提出了一种基于临界面正应力的多轴疲劳寿命预估方法，结合非比例加载下的影响因子，对整个预估过程进行了阐述。借助单个循环内应力响应状态随时间的变化曲线，得到各个时刻下的主应力方向，将不同时刻的应力投影至某一方向上，得到该平面主应力-时间变化曲线，并求解该方向上的疲劳损伤。根据损伤值加权平均，得到临界面的期望角度，并预测了疲劳寿命。

2）在随机振动疲劳中，对比了临界面疲劳预测寿命与多轴加速度随机振动试验的疲劳结果，寿命误差基本处于2 倍界范围内，验证了方法的有效性。其中，非比例加载强化效应还有进一步研究的空间。