连续突风频域响应过程的时域等效模拟方法
2020-10-09刘滢滢刘景光
刘滢滢,刘景光
(中国商用飞机有限责任公司上海飞机设计研究院 载荷部,上海 201210)
现代民用飞机尺寸变大后,结构的柔度增大[1],同时,飞机的飞行速度增加,巡航状态下的气动特性非线性特征增强[2]。突风载荷已成为民用飞机最重要的设计载荷情况之一,突风响应给出的全机载荷和过载对详细设计阶段和取证阶段都至关重要[3]。
突风和紊流载荷是民用航空规章[4]中飞行载荷的重要情况,分连续突风载荷及离散突风载荷两种。按中国民用航空规章CCAR-25§25.341 (a)(1)的规定,计算限制突风载荷时必须考虑结构弹性模态及刚体模态在内的多个模态,通过动态分析,给出结构各部分的载荷[5-7]。
按中国民用航空规章CCAR-25-R4$25.341 规定,离散突风的突风速度输入与突风梯度、高度、飞行速度、飞机载重情况有关[8],具有明确的相位及幅值信息。连续突风的突风速度输入与高度、飞行速度、飞机载重情况有关,输入为突风速度的功率谱密度形式,无明确的相位及幅值信息[9-10]。
离散突风分析给出全机载荷时域响应,同一时刻,全机载荷平衡;连续突风分析给出全机载荷频域的均方根,无明确的时域平衡载荷[11],为分析带来不便。一个连续突风分析工况对应无数的离散分析工况,两者结果应相符并可互相验证。若能将连续突风分析转化为离散突风分析,则可利用离散突风分析的优势,并弥补离散突风激励不足的劣势,增加突风载荷包线的分析精度,且频域分析的优势在于快速线性化分析,同时时域分析的优势是可考虑舵面偏转限制等多种非线性因素,进行较精确的非线性分析[12-14]。
连续突风速度一般采用 Von-karman 功率谱形式。将频域输入转化为时域输入的方法主要有三种,一是基于PSD 离散的逆Fourier 变换法,由D. Cebon首次提出,并在铁轨模拟中成功应用的[15];二是线性滤波方法[16],即白噪声滤波法,其用于满足特定条件的白噪声抽象指定的随机过程,然后适当变换假定系统而拟合出该随机过程的时域模型,得到一个代表性样本[17];三是谐波叠加法模拟[18],采用离散谱逼近目标随机过程的模型离散化数值模拟方法,只要频率间隔足够密,将对应各小区间的谐波函数累加,即得到随机过程的一个时域模型[19]。
将连续突风的输入功率谱密度分为若干频率间隔上的功率谱分布,为每段功率谱直接分配随机相位,得到频谱,进行傅里叶逆变换,得到时域上的突风速度输入,该时域激励与频域激励的功率谱密度相同。得到时域激励后,进行离散突风载荷分析,与连续突风载荷分析的结果对比,结果显示利用随机相位构造时域突风激励的方法快捷有效,便于进行非线性分析,能直观地显示随机突风激励的时域情况,同时,比较机翼的弯矩、剪力及扭矩,离散突风载荷分析得到的弯剪扭载荷值与连续突风载荷分析得到的弯剪扭载荷值的偏差不超过3%。
1 突风分析方法
频域中的突风响应分析,在模态坐标系中进行,其基本运动方程如下:
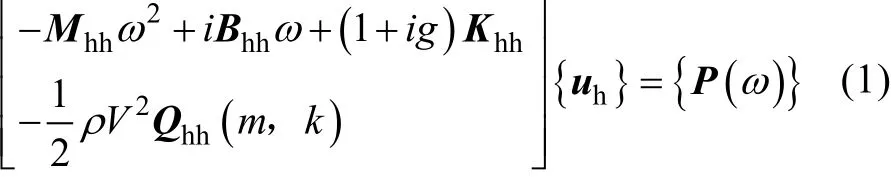
式中:Mhh为广义质量矩阵;Bhh为广义阻尼矩阵;为广义刚度矩阵;m为马赫数;k为减缩频率;c为参考弦长;为广义气动力系数矩阵;ω为圆频率;g为结构阻尼;ρ为大气密度;V为飞行速度;uh为模态幅值向量;为变换到模态坐标系的外激励。
中国民用航空规章CCAR-25§25.341 突风设计准则规定了民用飞机的突风激励形状,离散突风形状为1-cos 型的时域激励,连续突风采用功率谱密度输入的形式。
2 民用飞机单机翼连续突风响应
建立用于突风响应计算的民用飞机单机翼模型,进行垂向连续突风响应计算。
2.1 模型
民用飞机的单机翼结构模型如图1 所示,其机翼长16.24 m,展弦比为9。用部件弹性刚轴上的弹性梁模拟整个结构,其中,若干梁元模拟机翼的不同站位,用若干集中质量离散化结构质量及燃油质量,加载在梁元对应节点。对应气动模型如图2 所示,用720 个气动力面元模拟单机翼,采用MSC. Nastran 中的偶极子格网法计算非定常气动力,气动力与结构位移间的耦合通过样条函数实现。

图1 单机翼结构模型Fig.1 Structure model of single wing

图2 单机翼气动模型Fig.2 Aerodynamic model of single wing
2.2 突风功率谱输入及时域转化
突风速度为 1 m/s,突风速度功率谱输入采用Von-karman 谱,功率谱密度函数如下:

式中:Φ为大气紊流功率谱密度;σ为突风速度均方根值;Ω为折算频率,Ω=2πf/v;L为突风尺度(规范规定为760 m)。
取σ为1,功率谱密度频域曲线如图3 所示。

图3 突风功率谱密度输入Fig.3 Input of power spectral density of gust velocity
对图3 所示的功率谱密度,考虑输入时长为20 s的离散突风速度,选取1024 个未知的离散速度点进行拟合,目标是已知的功率谱密度函数。
由于时域突风速度输入x(t)的均方值可表示为:

其中,傅氏级数Ck满足:
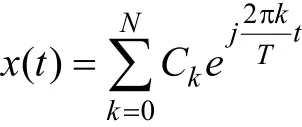
总时间T=20 s,总离散点数N=1024。时间离散点的均方根具有功率的含意,故示fk频率处,频率间隔为基频ω0,即1/T频段的功率谱分布。
针对式(2)中的功率谱密度函数,在0 至25.6 Hz 区间,每隔1/20 Hz 取一个频率点,共取513 个频率点,将各频率点上的值Φ(fk)乘以频率间隔1/T,得功率谱分布W(fk),考虑到单边功率谱的分布特征,上述频率序列中的1/20 至511/20 Hz,其功率谱分布为W(fk)/2,开根得Ck的模值,此时为1/20 Hz 至511/20 Hz 分配随机相位,得到Ck的估计值,随机相位位于0 至2π rad 之间,则513/20 至1024/20 Hz 频率点的Ck估计值与1/20 至511/20 Hz 对应频率点的Ck估计值共轭。
按上述方法得到0/20 至1024/20 Hz 频率点上的Ck后,进行傅里叶逆变换,可得到离散时域点,位于10 s 内,共1024 个离散点,分布如图4。
图4 中转化后的突风速度时域激励,包含低频及高频信号,具有确定的相位及幅值。

图4 突风速度时域激励Fig.4 Gust velocity time domain excitation
2.3 连续突风及离散突风结果对比
检查上述连续突风结果,机翼翼中的垂向弯矩、剪力及扭矩的均方根见表1。

表1 连续突风机翼翼中的均方根值Tab.1 Root mean square value of swing in continuous gust
采用2.2 节中生成的时域离散突风速度,进行垂向离散突风响应计算,机翼中段的垂向弯矩、剪力及扭矩时域响应曲线见图5。
施加图4 的突风激励后,机翼中段的弯矩、剪力及扭矩响应载荷如图5 所示,在10.5 s 左右,其弯矩、剪力及扭矩达到最大值,其中包含低频响应及高频响应,且随着图4 中的突风速度激励变化而变化。
对图5 中的弯矩、剪力及扭矩求其整个时域响应过程的均方根值,并与连续突风在频域响应过程中得到的载荷进行对比,结果见表2。

图5 机翼中段的垂向弯矩、剪力及扭矩时域响应曲线Fig.5 Time domain response of bending moment,shearing force, torque at middle part of the wing:a) bending moment, b) shearing force, c) torque

表2 离散突风机翼翼中的均方根值及差异Tab.2 Root mean square value and difference in discrete gust wing
表2 显示离散突风载荷分析得到的弯剪扭载荷值与连续突风载荷分析得到的弯剪扭载荷值的偏差不超过3%。
结合图5,在功率谱密度函数等效的基础上,利用随机相位构造时域突风激励的方法快捷有效,能直观地显示随机突风激励的时域情况,便于进行非线性分析。
3 结论
1)给出一种工程中实用的给定功率谱密度函数,拟合等效时域输入的方法,拟合后的突风速度时域激励频率含低频及高频。
2)通过数值拟合,建立连续突风分析与离散突风分析的关系,结果显示离散突风载荷分析得到的弯剪扭载荷值与连续突风载荷分析得到的弯剪扭载荷值的偏差不超过3%。
3)通过拟合连续突风的突风功率谱密度输入为等效的时域输入,可发挥两者优势。连续突风分析频率范围广,但不直观,无法给出明确的时域平衡载荷,且无法直接考虑非线性;离散突风分析给出全机载荷时域响应,同一时刻,全机载荷平衡,但分析频率范围有限。
