四自由度同步外差干涉测量系统设计
2020-10-09张善婷郭汉明
张善婷,郭汉明
(上海理工大学 光电信息与计算机工程学院,上海 200093)
引 言
随着超精密加工和生物医学工程等高新技术的发展,对激光干涉测量技术提出了更高的要求[1−2]。既要求测量行程大又要求达到纳米级的测量精度,同时需要对有位移的部件的其他自由度进行精密测量和严格控制。自20 世纪70 年代以来,多自由度同步检测技术得到了快速发展,根据光学原理的不同可以分为以下几种:基于光栅分束[3]、基于全反射测角法[4]、基于激光动态跟踪定位[5]以及基于激光干涉和准直相结合技术[6−7]。众多方法中仍存在各自的不足,例如:Ni 等[8]设计的三光束同时测量五自由度的系统,虽然能够实现角度和直线度的测量,且精度分别可达0.5″与1 μm,但是光路结构复杂,而且会受到光强变化和环境因素的影响;Yan 等[9]设计的能同时测量位移和角度的三自由度双外差干涉仪,由于目标反射镜的安装与运动误差以及干涉臂的光路长度不是绝对相等,使测量误差随着各向异性和非均匀环境波动而增加;Fan 等[10]用四套多普勒位移测量仪和L 型反射镜等来实现四光束基准的六自由度测量,成本较高;Lee 等提出的一种六自由度运动误差同步检测技术,是基于光栅干涉,角度测量精度达0.03'',直线度和位移测量精度分别为20 nm 和0.4 nm,但测量范围有限,不能满足大行程的需求。
为解决上述问题,本文设计了一种四自由度同步检测的外差干涉测量系统。该系统通过楔面棱镜和平面镜的组合,并结合差分波前传感技术,能够实现四自由度同步检测,其测量精度高、行程大,能够避免其他自由度的串扰误差。
1 系统组成
用于同时测量直线度、位移、俯仰角、偏转角的干涉仪测量系统如图1 所示。
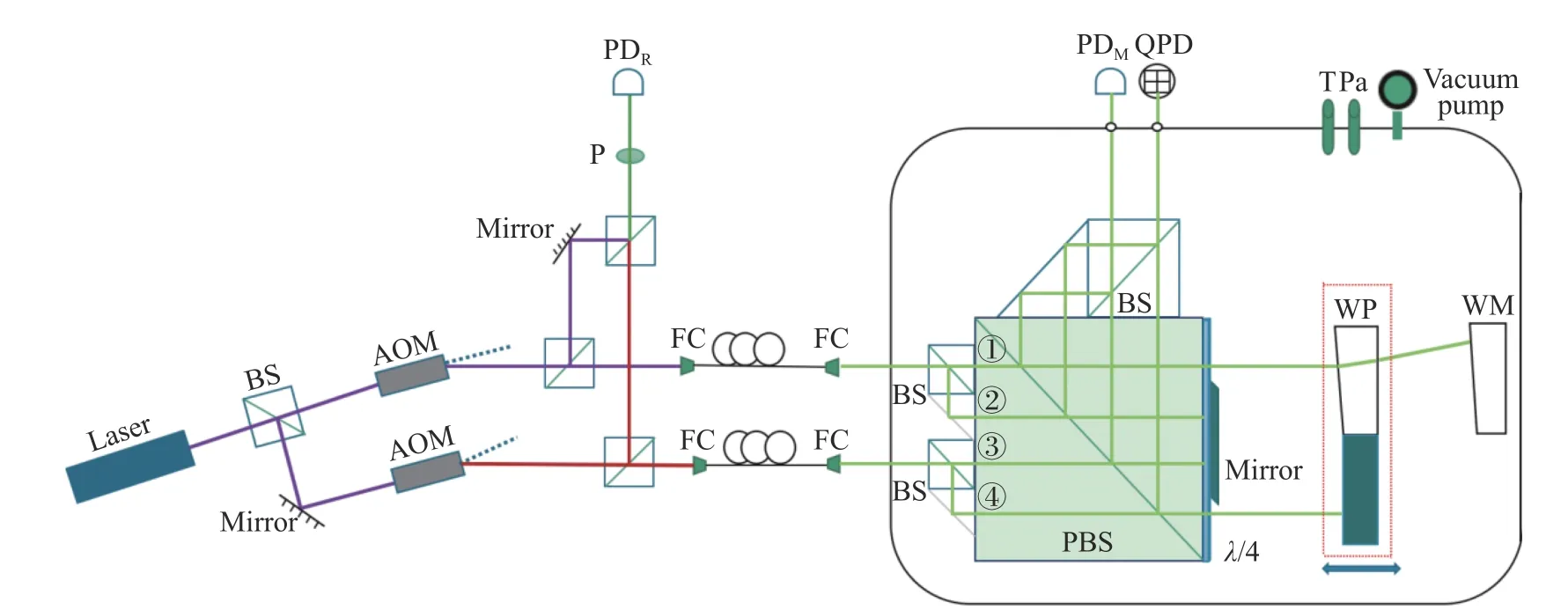
图1 四自由度外差干涉测量系统Fig.1 Measurement system for four degrees of freedom heterodyne interference.
该系统主要由532 nm 固体激光器、楔面棱镜、楔面反射镜和差分波前传感器等组成。以中国计量大学研制的小型化碘稳频532 nm 固体激光器为光源,运用调制转移光谱技术[11],将频率锁定到国际计量委员会推荐的复现米定义谱线R(56)32-O(a10)上,具有很好的溯源性[12]。楔面棱镜(WP)的楔角为1°,是直线度传感元件[13]。楔面反射镜(WR)的楔角近似为0.5°,与楔面棱镜配套,是回光元件,使光线能够原路返回,并且其尺寸大小决定了该系统的测量行程可达6 m。与楔面棱镜一同固定在线性平移台上的还有一个平面反射镜,两者共同构成系统的测量目标镜。光束经过该平面镜后将携带的位移、俯仰角和偏转角等信息传到四象限探测器上,结合差分波前传感技术以及探测器的几何形状和每个象限中的干扰相位,分离和测量目标镜的位移、俯仰角和偏转角的变化。
光源发出的波长为532 nm 的一束激光,经分光棱镜后被分成光强相等的两束激光,之后该两束激光分别通过驱动频率为80 MHz 与82 MHz的声光调制器(acousto-optic modulator,AOM),仅保留+1 级衍射光,则经过AOM 的两束激光具有2 MHz 的频率差。两束一级衍射光(频率记为 f1和 f2)分别经过分光棱镜,一部分引入参考光电探测器(PDR)作为参考光束,另一部分耦合进保偏光纤中,然后再准直回到自由空间。通过光纤耦合技术将两束空间光分离,这样能够抑制双频光混叠引起的非线性误差。调整光束偏振方向,使光束的偏振方向均平行于纸面,最后将光束输入真空腔。
两束激光经过分光棱镜和反射镜后分为光强相等的四束光,分别记为①、②、③、④。这四束光都透过偏振分光棱镜,各自通过 λ/4 波片后,光束①经过楔面棱镜和楔面反射镜,光束②、③、④直接被反射镜反射,之后四束光均原路返回,再次通过λ/4 波片。由于所有的λ/4 波片快轴方向与纸面的夹角都是45°,往返两次透过λ/4 波片后,四束光的偏振态都旋转了90°且垂直于纸面。通过偏振分光棱镜时,四束光都被反射,利用反射镜和分光镜将四束光两两合光。光束①和③合光后的拍频信号进入测量光电探测器(PDM),然后测得测量信号与参考信号之间的相位差就可实现直线度测量;光束②和④合光后的拍频信号进入四象限探测器(QPD),然后测得测量信号与参考信号之间的相位差就可实现位移,俯仰角和偏转角的测量。
2 测量原理
2.1 直线度测量
直线度的测量值反映在光程差的变化中。频率分别为 f1和 f2的两束激光①和③分别经过不同的路径,从而携带有不同的光学相位信息。当两束激光再度会合时,形成拍频干涉测量信号,将其与参考信号(f1−f2)进行相位比较,则可得到相位差 Δ φ 和被测位移即光程差 Δl 之间的线性关系

式中:λ 为激光的中心波长;n 为折射率。楔面棱镜移动时,直线偏移引起直线度传感器中光路的变化如图2 所示。图2(a)为光束①沿光轴方向在楔面棱镜上的投影,实线框表示楔面棱镜发生直线偏移前的位置,虚线表示楔面棱镜偏移后发生位移d 的位置。如果光束同棱镜一起移动,则它们的位置应从T 移至T ′。从y 轴方向观察,如图2(b)所示,即原光束应移至的位置,但实际上光束并未移动,故可以看作光束 f1向内偏移,即经过的玻璃路程减少,也就是光程减少。
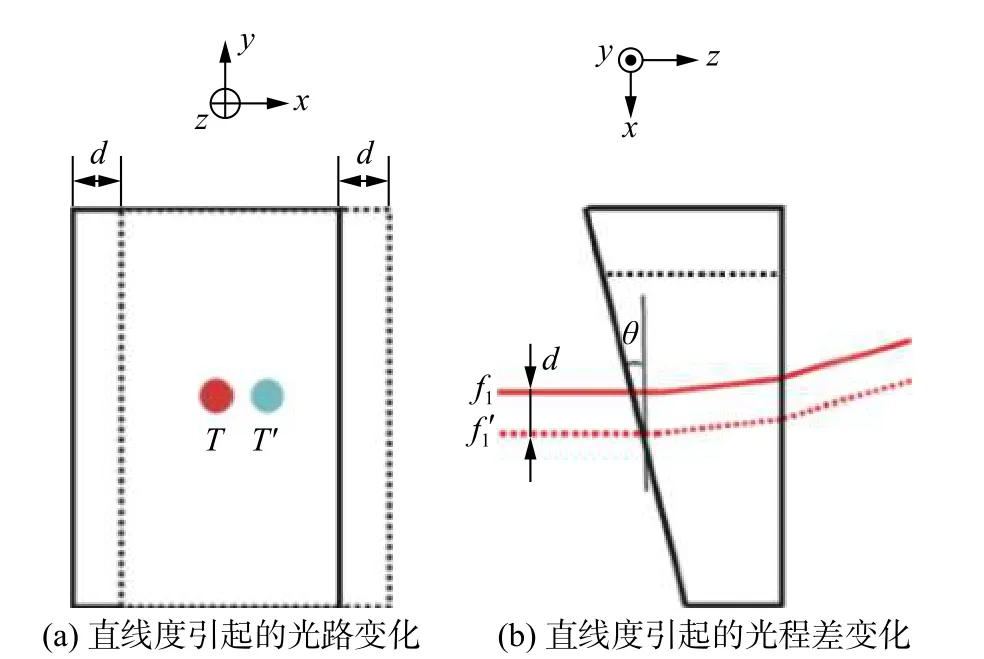
图2 直线偏移引起直线度传感器中光路的变化Fig.2 Change of light path in straightness sensor caused by straight line migration
假设光束通过楔角棱镜路程的变化量为l,楔角棱镜的楔角为θ,则有

式中l 与光程 Δl 直接相关。由于光束①先后两次穿过楔角棱镜,所以总光程差 Δl 与l 的关系为

式中:ng为玻璃折射率; na为空气折射率。设玻璃折射率近似为1.5,空气折射率近似为1,则可以得到楔面棱镜的直线度为
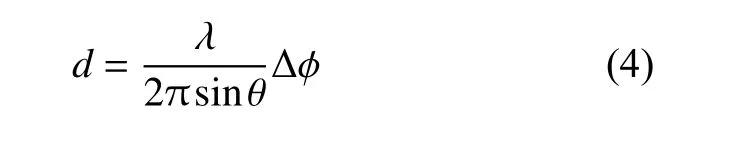
式(4)为直线度与相位差之间的关系式,通过相位计测得测量信号与参考信号之间的相位差即可求出系统直线度误差。假设所用楔面棱镜的楔角 θ 为1°,相位计的分辨率为 2 π/2048 ,激光中心波长为532 nm,则根据式(4)可求得直线度的测量分辨率为14.88 nm。
2.2 位移、俯仰角及偏转角测量
差分波前传感(DWS)是一项较新的技术,其应用越来越广泛,主要用于光学对准领域[14-15]。DWS 利用四象限光电检测器(见图3),从干涉波前检测并计算出相对于参考光电探测器的每个象限的相位变化。如果仅发生平移,则四个象限的相移将相同,所以总位移正比于所有象限之间的相位平均值。但是,如果两个波前之间存在角度变化,则相移在每个象限之间是不同的。因此,使用对称的相邻检测器的相位加权平均值可以获得俯仰角和偏转角的测量值。设线性平台的位移为z,俯仰角为 α ,偏转角为 β ,则这三个自由度计算式如下:

式中:φA,φB,φC,φD分别为四个象限的检测 相 位;Lp=2h/Sp,Ly=2w/Sy,其 中2h 和2w 为四象限光电探测器的几何尺寸(见图3),Lp和 Ly代表俯仰角和偏转角测量中的等效长度,主要取决于光束直径、探测器大小、对准误差及光束波前,而变量 Sp和 Sy是分别确定俯仰角和偏转角等效长度的比例因子。
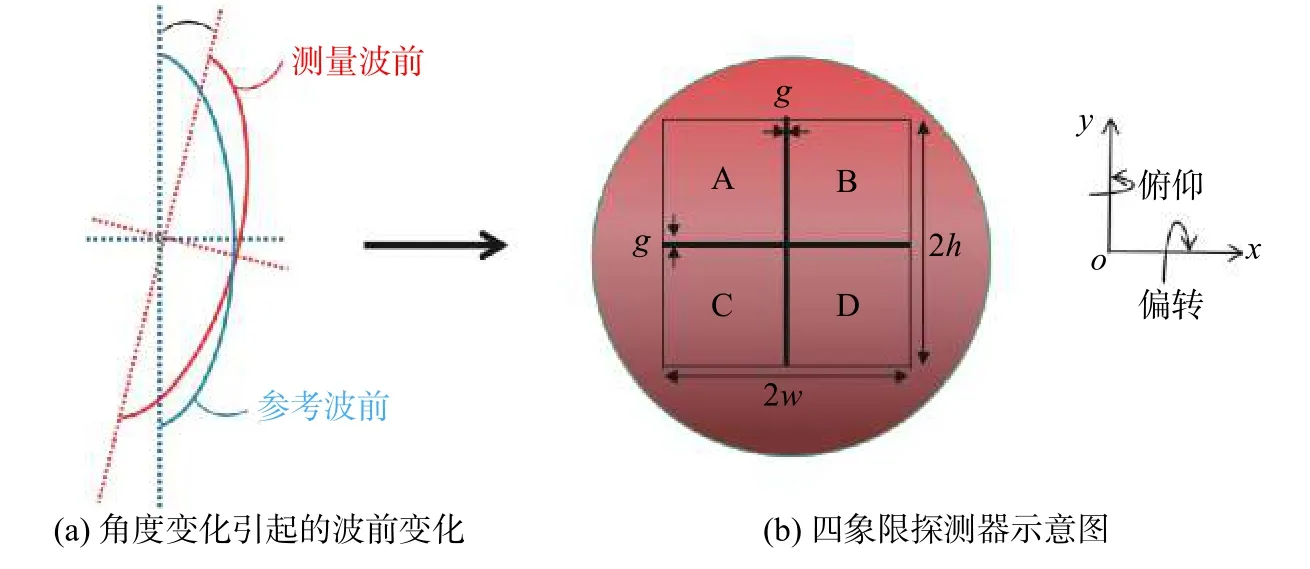
图3 带有倾斜测量波阵面的差分波前传感的四象限探测器示意图Fig.3 Schematic diagram of a four-quadrant detector for differential wavefront sensing with tilt measurement wavefr ont.
用四象限探测器检测光束②和④在各个象限的相位变化,根据式(1)可以转换出位移信息,即

将四个象限上的四个相变值(φA,φB,φC,φD)转换为四个位移值(zA,zB,zC,zD)后,理论上可将俯仰角表示为
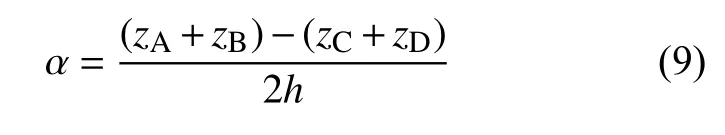
同理可得偏转角为

假设四象限探测器的尺寸为 5 mm×5 mm ,则理论上位移测量分辨率为0.13 nm,偏转角和俯仰角的测量分辨率为0.026 μrad。
2.3 测量行程分析
图4 是从y 轴方向上观察到的光束经过楔面棱镜和楔面反射镜的路径,设楔面棱镜和楔面反射镜的楔角分别为θ 和 δ ,其中θ=1°。测量光束从楔面棱镜A 点入射,经过楔面棱镜后在B 点出射,然后到达楔面反射镜C 点后反射,此时有最大测量行程 Lmax。根据几何关系可得楔面棱镜可移动的最大长度为

图4 经过楔面棱镜和楔面反射镜的光路俯视图Fig.4 Top view of light path passing through wedge prism and wedge mirror

式中:L 为楔面棱镜的长度; Lmin为楔面反射镜的最小尺寸。当测量光束直接从楔面棱镜A'点入射,B'点出射,之后落在楔面反射镜上的C'点,此时可得楔面棱镜的最小尺寸Lmin为
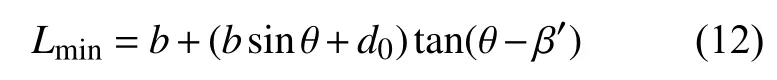
式中:b 为光束到楔面棱镜窄处的距离; β′为光束射入楔面棱镜时的折射角; d0为楔面棱镜窄处的厚度。根据折射定律有

由 ng= 1.5,na=1,得到 t an(θ −β′)≈0 ,则

结合式(11)得

设 δ=30'59'',L=60 mm,b=5 mm,代入式(15)得 Lmax≈ 6 302.6 mm。由此可见,根据所选器件尺寸搭建的测量系统,可以在6 m 行程内实现四自由度的测量。
3 误差分析
3.1 系统误差分析
楔面棱镜是直线度测量的敏感器件,而楔面反射镜是与楔面棱镜配套使用且使光束原路返回的重要元件。如果楔面棱镜和楔面反射镜本身存在加工误差,可能会导致光束不能原路返回,就会导致直线度的测量结果存在偏差。在实际测量过程中,由于无法保证完美的光束对准,所以光束对准误差不可避免会对测量结果造成影响。
一同固定在线性平台上的楔面棱镜和楔面反射镜,在安装时可能存在激光测量轴与被检设备的运动轴不重合的情况,产生的余弦误差使得测量距离比实际距离要短[13]。假设线性平台的实际位移量为L,γ 为理论位移路径与实际位移路径的夹角,则所测得的位移量L′与L 的关系为L′=Lcosβ。该误差可消除,不会影响测量分辨率。
3.2 系统环境误差分析
在高精度激光测量系统中,要求将实际工作环境控制在较为严格的范围内,其中环境控制的主要指标为空气的温度、压力以及相对湿度等[16]。当环境中的这些因素改变时,空气折射率会发生变化,进而影响测量精度。为了减少以及控制环境因素对测量结果的影响,整个测量过程均在真空腔内进行,实时监测并控制腔内环境因素的变化。由于测量过程一般在短时间内就能完成,因此选择能在短时间内保持空气折射率不变或近似不变的真空腔,就可以减少环境误差对测量分辨率的影响。
3.3 阿贝误差分析
在大行程高精度定位装置中(如光栅刻划工作台、光刻机的扫描定位工作台、大范围扫描探针显微镜),因不可避免地存在角运动误差(偏转角、俯仰角、滚转角),对测量结果造成影响,所以必须对测量过程中的角运动误差进行精密测量和严格控制。很明显滚转角不会对该系统的位移、俯仰角及偏转角的测量造成影响。在直线度测量中,当角分量存在时(大约在μrad 级别),光束入射到楔面棱镜上的入射角及出射的折射角等都会产生很小的变化,不利于分析。所以基于光线近似原路返回,我们来分析角分量引起直线度测量的阿贝误差。
当楔面棱镜沿y 轴旋转运动时,即有偏摆角的存在,使得光程差发生了变化。图5 为楔面棱镜偏摆引起的光程变化示意图,楔面棱镜偏摆角为 β ,楔面棱镜由实线位置旋转到虚线位置,光束在z 轴上的相对位置变化量为 D=btanβ ,如图5(a)所示,由此引起的系统光程差变化如图5(b)所示。此时光程差的变化为

式中 ψ 为光从楔面棱镜出射时的折射角。设楔面棱镜的楔角α= 1°,材料为K9 玻璃,所以ψ=0.51°。以PI 公司的M-404.42S 仪器为例,其偏摆角为 β=400 μrad,得出 Δl= 0.08 nm,总的光程差为 Δ L=2Δl=0.16 nm。总光程差与所能测得的 最小 直线 度 d=14.88 nm 相比,可以 忽 略不计,因此偏摆角不会引起直线度测量误差。

图5 楔面棱镜偏摆引起的光程变化Fig.5 Optical path change caused by wedge-angle prism deflection
当楔面棱镜沿x 轴旋转运动时,即俯仰角的存在,引起的光程变化如图6 所示。光线垂直于棱镜的横截面入射,棱镜绕x 轴旋转了α 角,即俯仰角为α,沿x 轴方向出射光与入射光在同一水平线,如图6(a)所示。光线入射到楔面棱镜时的折射角记为 α ,如图6(b)所示,根据折射定律有 nasinα=ngsinα ,当 α=400 μrad 时,经计算得 α 近似为267 μrad。俯仰角引起的光程差变化为
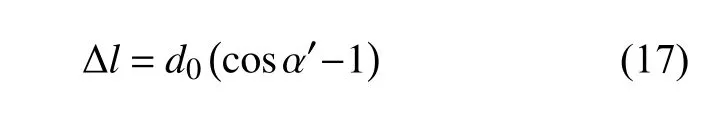
式中 d0为楔面棱镜窄处的厚度。假设 d0=5 mm,则总光程差 Δ L=2Δl=0.34 nm,对直线度的影响可忽略不计,所以俯仰角不会造成直线度测量误差。
图7 为滚转角引起的楔面棱镜中的光路变化示意图,假设有滚转角的存在,使棱镜从实线位置旋转了 σ 角度至虚线位置,如图7(a)所示。由滚转角引起y 轴上的位移差为 Δ y=a(1−cosσ) ,其中a 为光束在y 轴方向到楔面棱镜底端的距离。我们用光束的旋转代替棱镜的旋转,由图7(b)知滚转角引起的光程差变化为

图6 俯仰角引起的楔面棱镜中光路的变化Fig.6 Optical path changes in wedge-shaped prisms caused by elevation angle

假设a=5 mm,σ=400 μrad,则总光程差ΔL=2Δl=2×10−6nm,对直线度的影响可以忽略不计。
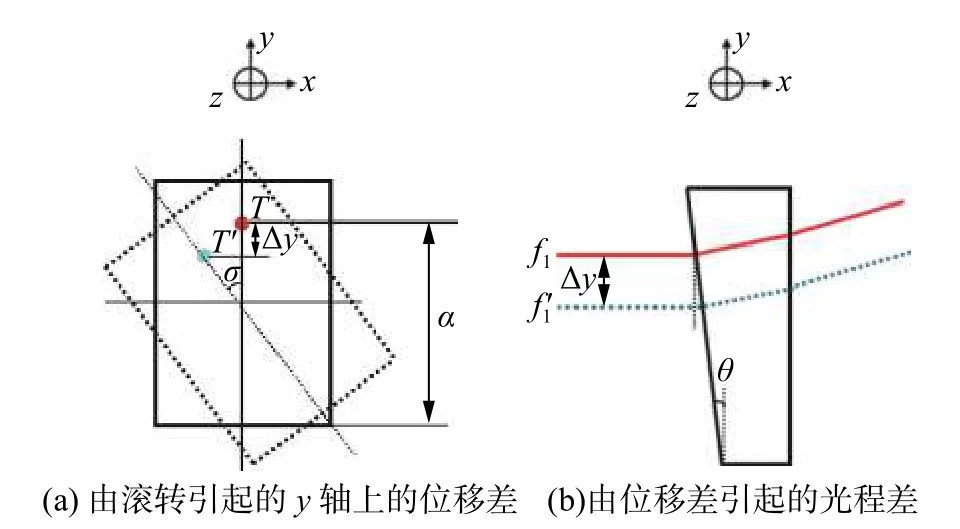
图7 滚转角引起的楔面棱镜中的光路变化Fig.7 Optical path changes in wedge prisms caused by roll angle
4 结 论
本文设计了一种大行程、高精度、四自由度同时测量的外差干涉测量系统。理论计算说明该系统在6 m 的量程内,位移分辨率达0.13 nm,偏转角和俯仰角分辨率达0.026 μrad,直线度测量分辨率达14.88 nm,具有四自由度同步检测的能力。与以往的激光干涉仪相比,该系统结构新颖简单,不仅能够实现高精度位移测量,还增加了直线度、偏转角及俯仰角三个自由度的同步检测。如果能同时保证特殊棱镜的精密加工精度,减少系统装配误差,保证光束对准,减少环境变动影响,克服参数之间的串扰,系统的测量精度还能得到更好的提高。
