不同测强曲线对混凝土抗压强度的影响及分析
2020-09-30朱靖林杨志刚李金耀李有元
朱靖林,商 波,杨志刚,李金耀,李有元
(云南建投第一勘察设计有限公司,云南 昆明 650102)
0 引言
混凝土作为我国建筑中一种广泛使用的材料,其抗压强度是否合格是关乎建筑物安全的重要因素。因此,科学、合理评定混凝土抗压强度等级,对于确定建筑物是否安全具有重要的意义。回弹法检测完毕后计算混凝土抗压强度推定值时测强曲线应如何选择,是评定混凝土抗压强度是否合格的重中之重。
目前国内已发表的文献中,行业标准 JGJ/T 23-2011《回弹法检测混凝土抗压强度技术规程》[1]和云南省地方标准 DBJ 53/T-52-2013《回弹法检测混凝土抗压强度技术规程》[2]两本标准的对比分析文献尚未出现,故本文结合实际工程项目的检测数据采用不同测强曲线对泵送混凝土抗压强度推定值进行计算和分析[3],对云南地区泵送混凝土抗压强度推定值计算具有重要意义。
1 两本标准的不同之处
行业标准 JGJ/T 23-2011《回弹法检测混凝土抗压强度技术规程》(以下简称“行标”)最新版本于2011 年 12 月 1 日开始实施;云南省地方标准 DBJ 53/T-52-2013《回弹法检测混凝土抗压强度技术规程》(以下简称“地标”)于 2014 年 1 月 1 日开始实施,对于同一个混凝土构件,采用行标中的全国统一测强曲线和地标中的测强曲线计算出的泵送混凝土抗压强度推定值存在一定的差异,本文就两者存在的差异进行一定的探讨。
1.1 行业标准
泵送混凝土在各方面与传统混凝土均存在很大差别。行标中,泵送混凝土的全国统一测强曲线方程为:
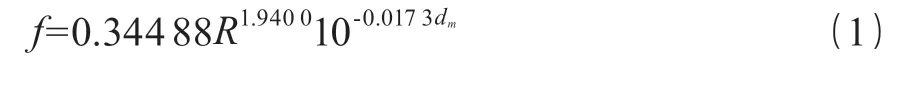
从式(1)可以得出,只需知道回弹强度平均值 R 和碳化深度 dm就能计算出混凝土强度换算值 f,根据行标中泵送混凝土的全国统一测强曲线方程采用 excel 可以绘出在 dm=1.0;dm=2.0;dm=3.0 时的曲线图(见图 1)。
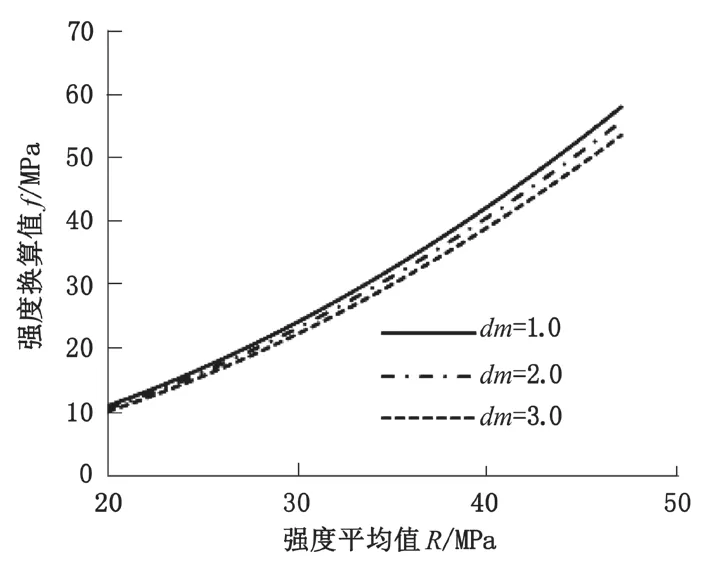
图1 行标中不同 dm 值对应的强度换算值 f
从图1中可以看出,泵送混凝土强度换算值 f 随着强度平均值R的增大而增大;在图中所给出的三种碳化值中,dm=1.0对应的强度换算值 f 最大;dm=2.0时对应的强度换算值 f 其次;dm=3.0 时对应的强度换算值 f 最小。
1.2 地方标准
地标中,泵送混凝土的测强曲线方程为:
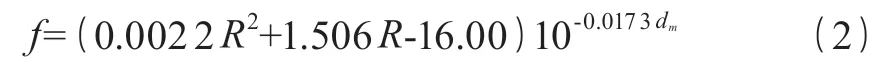
与行标中的全国统一测强曲线方程同理,只需知道回弹强度平均值 R 和碳化深度 dm就能计算出混凝土强度换算值 f,根据地标中的测强曲线方程采用 excel 可以绘出在 dm=1.0;dm=2.0;dm=3.0 时的曲线图如图 2 所示。
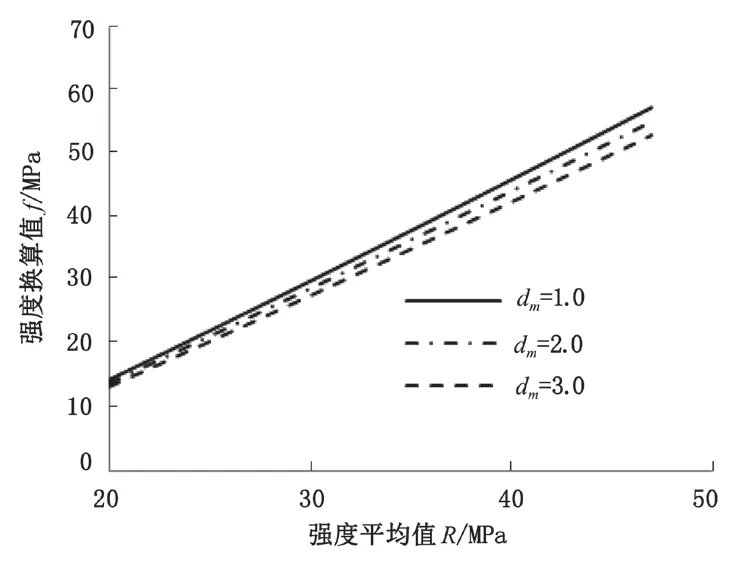
图2 地标中不同 dm 值对应的强度换算值 f
从图 2 中可以看出,强度换算值 f 随着强度平均值 R 的增大而增大;在图中所给出的三种碳化值中,dm=1.0 时对应的强度换算值 f 最大;dm=2.0 时对应的强度换算值 f 其次;dm=3.0 时对应的强度换算值 f 最小。
根据行标和地标中的相关条文说明,地标中给出的测强曲线方程的试验数据一共 11 557 组,其中绝大部分数据来自于昆明地区,在处理试验数据前,已将昆明地区以外的数据剔除,而后将剩下的 8 144 组数据采用最小二乘法进行处理,通过回归后得出测强曲线方程。行标中的全国统一测强曲线方程平均相对误差为±13.89 %;相对标准差 17.24 %;相关系数:0.878;地标中的测强曲线方程平均相对误差为±9.98 %;相对标准差 12.16 %;相关系数:0.906。两者相比,地标中的测强曲线方程强度误差值比全国统一测强曲线方程的强度误差值小,说明地标中给出的测强曲线方程在昆明地区具有良好的适应性和可靠性。地标中的测强曲线方程仅适用于昆明地区。
位于昆明地区的实际工程项目可以采用行标中的全国统一测强曲线计算泵送混凝土强度推定值,也可采用地标中的测强曲线计算泵送混凝土强度推定值。
2 工程实际应用
本次项目为昆明地区某水泥厂所有厂房混凝土质量检测,结合工程实际情况,本次检测采用回弹法,并测定各个构件的碳化深度值。所有厂房一共抽检 127 个混凝土构件,采用行标中的全国统一测强曲线和地标中的测强曲线分别对其进行计算和分析。
当碳化深度值 dm=1.0 时,用地标测强曲线和行标中的全国统一测强曲线分别计算,然后将得出的混凝土强度推定值 f 绘制成图(见图 3)。
当碳化深度值 dm=2.0 时,用地标测强曲线和行标中的全国统一测强曲线分别计算,然后将得出的混凝土强度推定值 f 绘制成图(见图 4)。

图3 碳化值 dm=1.0 时不同标准的计算结果

图4 碳化值 dm=2.0 时不同标准的计算结果

图5 碳化值 dm=3.0 时不同标准的计算结果
当碳化深度值 dm=3.0 时,用地标测强曲线和行标中的全国统一测强曲线分别计算,然后将得出的混凝土强度推定值 f 绘制成图(见图 5)。
从图 3、图 4 和图 5 可以得出,所有采用地标测强曲线计算出的混凝土强度推定值均大于所有采用行标中的全国统一测强曲线计算出的混凝土强度推定值。对比 127 个构件的计算结果,当碳化深度值 dm=1.0 时,地标测强曲线的计算结果平均值比行标中全国统一测强曲线的计算结果平均值大 5.4 MPa,两者的差距大约为22.4 %;当碳化深度值 dm=2.0 时,地标测强曲线的计算结果平均值比行标中全国统一测强曲线的计算结果平均值大 5.2 MPa,两者的差距大约为 22.2 %;当碳化深度值 dm=3.0 时,地标测强曲线的计算结果平均值比行标中全国统一测强曲线的计算结果平均值大 5.0 MPa,两者的差距大约为 22.1 %。两者的计算结果存在很大差异,地标测强曲线的计算结果比行标中的全国统一测强曲线的计算结果高出大约一个强度等级。
3 两种结果相差原因
上节提出,当回弹强度平均值 R 和碳化深度 dm值一定时,分别采用行标中的全国统一测强曲线和地标测强曲线计算混凝土强度推定值,所得结果相差 5 MPa 左右,二者的差距大约为一个强度等级。究其原因可得,两种测强曲线方程差别过大,具体原因分析如下:
行标中,泵送混凝土抗压强度推定值的全国统一测强曲线方程为:
f=0.344 88R1.940010-0.0173dm
地标中,泵送混凝土抗压强度推定值的测强曲线方程为:
f=(0.002 2 R2+1.506 R-16.00)10-0.0173dm
对比 2 个测强曲线方程可以得出,两个方程的不同之处在于 10-0.0173dm前的系数。将此系数用字母 A 表示,行标中的全国统一测强曲线方程中此系数为0.344 88R1.9400,即 A行=0.344 88R1.9400;地标测强曲线方程中此系数为(0.002 2 R2+1.506 R-16.00),即 A地=0.002 2 R2+1.506 R-16.00。
假设碳化深度值 dm一定,回弹强度平均值 R 的取值为 20≤R≤50 时,两个系数 A行和 A地的计算结果可用图 6 表示。
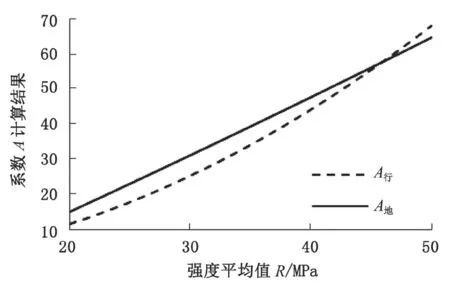
图6 A行和 A地计算结果对比图
从图 6 可以看出,两个系数 A行和 A地的计算结果随着强度平均值 R 的增大而增大。当强度平均值的取值为 20≤R<45.9 时,A行的计算结果均小于 A地的计算结果,强度平均值 R=30 时,两者的计算结果相差最大,取 R=30 作为中间值,当20≤R<30时,A行与 A地的计算结果差值逐渐增大;当30<R≤45.9时,A行与 A地的计算结果差值逐渐减小;当强度平均值 R=45.9 时,A行的计算结果约为 57.8,A地计算结果约为 57.8,两个系数的计算结果相等;当强度平均值的取值为 45.9<R≤50 时,A地的计算结果小于 A行的计算结果,且两者的计算结果差值逐渐增大。
由此可得,当回弹强度平均值 R<45.9 时,采用行标中的全国统一测强曲线计算混凝土强度推定值 f 小于地标测强曲线计算混凝土强度推定值 f;当回弹强度平均值 R>45.9 时,采用行标中的全国统一测强曲线计算混凝土强度推定值 f 大于地标测强曲线计算混凝土强度推定值 f;当回弹强度平均值 R=45.9 时,采用行标中的全国统一测强曲线计算的混凝土强度推定值 f 与采用地标测强曲线的计算结果相等。
4 结语
本文就行业标准 JGJ/T 23-2011《回弹法检测混凝土强度抗压技术规程》和云南省地方标准 DBJ 53/T-52-2013《回弹法检测混凝土抗压强度技术规程》计算泵送混凝土抗压强度推定值进行对比分析,分析了碳化深度 dm、平均回弹值 R 对混凝土强度推算值 f 的影响。并采用行标中的全国统一测强曲线和地标的测强曲线对实际工程项目进行计算,并对计算数据进行处理后得到以下结论:地标测强曲线的计算结果均大于行标中全国统一测强曲线的计算结果,前者大于后者 5 MPa 左右,两者的计算结果相差大约一个强度等级。
因地标中测强曲线方程的试验数据仅来自于昆明地区(昆明地区以外的数据已剔除),故地标中的测强曲线仅适用于昆明地区,昆明地区的实际工程项目既可以采用行标中的全国统一测强曲线计算泵送混凝土强度推定值,也可采用地标中的测强曲线计算泵送混凝土强度推定值。
行标的相关条文说明中提及了全国各地区可根据各地的气候、原材料等特点建立自己的测强曲线或专用曲线。地标已经经云南省住房和城乡建设厅批准,并于 2014 年 1 月 1 日开始实施。因此,昆明地区的实际工程项目在选取测强曲线时,可优先考虑地标中的测强曲线。除昆明地区以外,云南省其他地区只可采用行标中的全国统一测强曲线计算泵送混凝土抗压强度推定值。
