深刻理解概念准确描述运动

成树明

我们生活在一个随处可见物体运动的世界里，只有深刻理解质点、参考系、时刻、时间间隔、路程、位移、速度、加速度等物理概念和物理量，才能准确描述物体的运动。下面就对这些物理概念和物理量进行梳理和拓展，以期达到帮助同学们加深理解的目的。

一、质点

1.质点不同于几何“点”：质点是用来代替物体的有质量的点，其特点是只有质量，不考虑其大小和形状，几何中的“点”仅仅表示空间中的某一位置，二者有本质上的区别。

2.质点是一种“物理模型”：物理模型是在物理研究中，为了研究问题方便，突出问题的主要方面，忽略次要因素而建立的理想化模型(实际并不存在)，质点就是典型的物理模型之一。

例1研究下列现象，涉及的物体可看成质点的是( )。

A.研究动车通过桥梁的时间

B.研究动车从上海开往昆明的时间

C.研究地球绕太阳公转的时间

D.研究“嫦娥四号”探测器在轨道上进行姿态调整

研究动车通过桥梁的时间，不能忽略动车的长度，因此不能将其看成质点，选项A 错误。研究动车从上海开往昆明的时间，可以忽略动车的大小和形状，因此可以将其看成质点，选项B 正确。研究地球绕太阳公转的时间，地球的大小远小于日地距离，其形状和大小可以忽略，因此可以将其看成质点，选项C正确。研究“嫦娥四号”探测器在轨道上进行姿态调整，其形状和大小不能忽略，因此不能将其看成质点，选项D 错误。答案为BC。

分析物体能否被看成质点需要视研究的具体问题而定，而不能只看其大小，很小的物体不一定能被看成质点，很大的物体也可能被看成质点。

二、参考系

1.选择参考系的意义：要描述一个物体的运动，必须先选取参考系，之后才能确定物体做怎样的运动。

2.选取参考系的方法：研究物体的运动时，参考系是可以任意选取的，但一般根据研究问题的方便性来选取。比如，研究地面上物体的运动时，常选地面或相对于地面静止的物体作为参考系。

注意：在解题过程中，选地面作为参考系时可以不指明，但选其他物体作为参考系时必须指明。

3.参考系的四个特性：(1)任意性，参考系可以任意选取，但不能选自身为参考系；(2)标准性，被选作参考系的物体都是假定不动的，其他物体的运动情况都是相对于参考系而言的；(3)差异性，选择不同的参考系，对同一物体运动的观察结果可能不同；(4)同一性，比较不同物体的运动时，必须选择同一参考系。

4.选取参考系的原则：在实际问题中，以观测方便和使运动的描述尽可能简单为原则。比如，研究地面上物体的运动时，常选地面或相对地面静止的物体作为参考系；研究某一系统中物体的运动时，常选这个系统为参考系。

例2下列关于运动的描述中，正确的是( )。

A.诗句“卧看满天云不动，不知云与我俱东”中“云与我俱东”是以船为参考系的

B.“明月松间照，清泉石上流”是以山石为参考系的

C.“太阳东升西落”是以太阳为参考系的

D.升国旗时，观察到国旗冉冉升起，是以旗杆为参考系的

选项A 中的研究对象是“云与我”，是以两岸为参考系的，选项A 错误。选项B中的研究对象是“泉水”，是以山石为参考系的，选项B 正确。选项C中的研究对象是“太阳”，是以地球为参考系的，选项C 错误。选项D 中的研究对象是“国旗”，是以地面或旗杆为参考系的，选项D正确。答案为BD。

判断参考系的两种方法：一是静物法，即在可以明确观察到的现象中，先确定什么物体是运动的，什么物体是静止的，其中静止的物体可能就是参考系；二是假设法，即假设以某物体为参考系，看对物体运动的描述是否与描述中的结果一致，若一致，则该物体可能就是参考系。

三、时刻与时间间隔

表1 时刻与时间间隔的区别和联系

注意：在物理学中，“时间”的含义就是时间间隔。在日常生活中所说的“时间”，其含义不尽相同，有时是指时刻，有时是指时间间隔，要根据上下文认清它的含义。

例3关于时刻和时间间隔，下列说法中正确的是( )。

A.8点上课，8点是上课的时间

B.1分钟内有60个时刻

C.“宁停三分，不抢一秒”指的是时间

D.北京开往广州南的高铁列车9 时23分从北京西站发车，9时23分是时刻

8点上课，8点是指时刻，选项A 错误。1 分钟内有无数个时刻，选项B错误。“宁停三分，不抢一秒”中的三分和一秒均指时间间隔，选项C 正确。北京开往广州南的高铁列车9时23分从北京西站发车，9时23分是时刻，选项D 正确。答案为CD。

在时间轴上，时刻对应时间轴上的一点，时间间隔对应时间轴上的一段线段。描述物体的运动时，时刻对应物体的某一位置，时间间隔对应物体的一段运动过程。

四、路程和位移

表2 路程和位移的区别和联系

易错提醒：(1)若某段时间内某物体通过的路程为零，则这段时间内这个物体一定静止，其位移也一定为零。(2)若某段时间内物体的位移为零，则这段时间内这个物体不一定静止，可能是经过运动返回到了出发点，其路程不一定为零。(3)物体运动轨迹的长度即为路程，是标量；位移只取决于物体的初、末位置，与运动轨迹无关，是矢量。(4)用坐标系表述物体的位置及位置变化时，要先建立坐标系并规定正方向，再用正、负数表示矢量。“+”号表示与规定的正方向一致，“-”号表示与规定的正方向相反；数字的大小表示矢量的大小。

例4如图1所示，一个人晨练，走半径为R的八卦图运动，中央的“S”形部分是两个直径为R的半圆。他从A点出发沿曲线ABCOADC行进。求：

(1)他从A点第一次走到O点时的位移的大小和方向。

(2)他从A点第一次走到D点时的位移和路程。

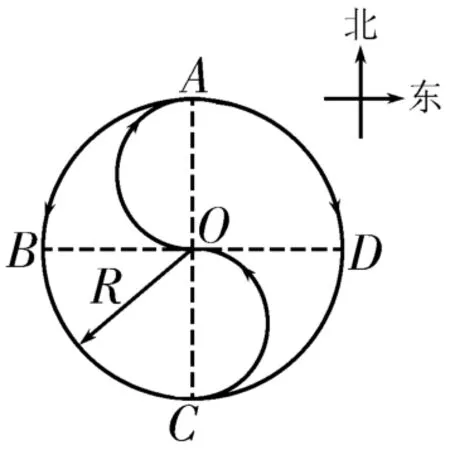
图1

(1)他从A点第一次走到O点时的位移的大小等于线段AO的长度，即x1=R，方向由北指向南。

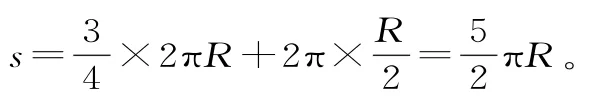
位移的两种计算方法：一是几何法，即根据位移的定义先画出有向线段，再利用几何知识计算；二是坐标法，即写出初、末位置坐标，用末位置坐标减初位置坐标得到的结果就是位移，结果中的正、负号表示位移的方向。

五、速度

1.对概念的理解：高中阶段对速度的定义是运动物体的位移与所用时间的比值，而不是初中阶段所学的路程与时间的比值。实质上，这两种对速度的定义并不矛盾，因为初中阶段只研究匀速直线运动，且不需要考虑运动方向，则路程等于位移的大小。

2.速度的矢量性：速度既有大小，又有方向，是矢量。瞬时速度的方向就是物体在此时刻的运动方向。比较两个速度是否相同时，既要比较其大小是否相等，又要比较其方向是否相同。

3.平均速度与瞬时速度的区别和联系：平均速度是过程量，表示物体在某段时间或某段位移内的平均运动快慢程度；瞬时速度是状态量，表示物体在某一时刻或某一位置的运动快慢程度。瞬时速度是运动时间Δt→0时的平均速度，体现了极限的思想方法。

4.平均速度与平均速率的大小关系：平均速度的大小不等同于平均速率，因为平均速率是路程与时间的比值，只有当路程与位移的大小相等时，平均速率才等于平均速度的大小。

例5一辆汽车沿平直的公路单向行驶，从A处行驶到B处用了60s，A、B两地相距900m；在B处停留30s后沿原路返回，用了45s到达A、B的中点C处。求：

(1)汽车前60s内的平均速度。

(2)汽车从A处出发到最终返回C处的平均速率。

六、加速度

加速度是速度的变化量Δv与发生这一变化所用时间Δt的比值，在数值上等于单位时间内速度的变化量(速度的变化率)。

注意：加速度和速度、速度变化量的大小均没有必然的联系。

例6一个做变速直线运动的物体，其加速度逐渐变小，直至为零，那么该物体运动的情况可能是( )。

A.速度不断增大，当其加速度为零时，速度最大

B.速度不断减小，当其加速度为零时，速度最小

C.速度的变化率越来越小，当其加速度为零时，速度不再改变

D.速度肯定是越来越小的

当加速度方向与速度方向相同时，物体做加速度减小的加速运动，当其加速度为零时，速度最大，此后做匀速直线运动，选项A 正确，D 错误。当加速度方向与速度方向相反时，物体做加速度减小的减速运动，当其加速度为零时，速度最小，此后做匀速直线运动，选项B正确。加速度逐渐变小，单位时间内的速度变化量逐渐减小，即速度的变化率越来越小，当其加速度为零时，速度不再改变，选项C正确。答案为ABC。

判断做直线运动物体速度变化情况的方法如图2所示。

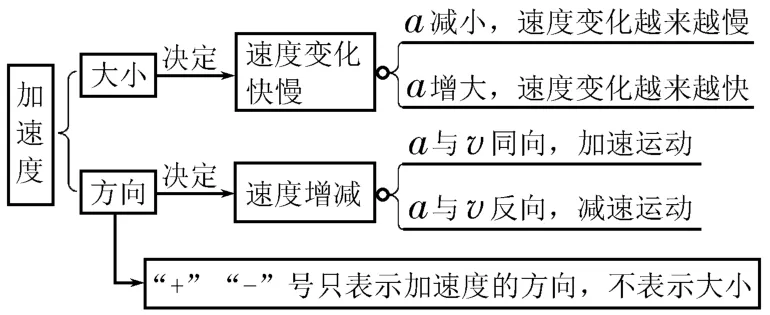
图2

例7物体以6m/s的初速度沿光滑斜槽向上做直线运动，经6s滑回原处时速度大小仍为6m/s，求此过程中：

(1)物体的速度变化大小和方向。

(2)物体的加速度大小和方向。

(1)取物体的初速度方向为正方 向，则v0=6m/s，vt=-6m/s，Δv=vt-v0=-12m/s。因此物体的速度变化大小为12m/s，方向沿斜面向下(与初速度方向相反)。

1.2018年11月，第十二届中国国际航空航天博览会在广东珠海如期举行，首次亮相航展的空军航空大学“红鹰”飞行表演队为现场观众带来了“八机钻石筋斗”“丘比特之箭”等精彩动作。下列关于“红鹰”飞行表演队的说法中正确的是( )。

A.地面上的人看到飞机飞过，是以飞行员为参考系的

B.飞行员看到观礼台向后掠过，是以飞机为参考系的

C.研究某架飞机在空中飞行的轨迹时，可将飞机视为质点

D.研究飞机在空中的各种表演动作时，可将飞机视为质点

2.足球运动员在罚点球时，球由静止至被踢出时的速度为30m/s，脚与球作用的时间为0.15s，球在空中的运动可视为匀速直线运动，球在空中飞行一段距离后被守门员挡出，守门员双手与球接触的时间为0.2s，且球被挡出后以10m/s的速度沿原路反弹。设球与罚点球运动员的脚或守门员的手接触的时间内加速度恒定，求：

(1)在罚点球运动员的脚与球作用的时间内，球的加速度的大小。

(2)在守门员挡球的时间内，球的加速度的大小和方向。

3.有一辆汽车沿笔直公路行驶，第1s内向东行驶5m 的距离，第2s内和第3s内继续向前各通过20m 的距离，第4s内又前进了15m 的距离，第5s内反向通过30m 的距离，求：

(1)5s内的路程。

(2)5s内的位移大小及方向。

(3)最后2s内的平均速度和平均速率。

参考答案：

1.BC

2.(1)200m/s2。(2)200m/s2，方向与球被踢出后的方向相反。

3.(1)90m。(2)30m，方向与汽车开始运动时的方向相同。(3)7.5m/s，方向与汽车开始运动时的方向相反；22.5m/s。