Simulation of the Power Take-off System for a Heaving Buoy Wave Energy Converter
2020-09-29CAOFeifeiSHIHongdaLIMingDONGXiaochenandLIDemin
CAO Feifei, SHI Hongda, *, LI Ming, DONG Xiaochen, and LI Demin

Simulation of the Power Take-off System for a Heaving Buoy Wave Energy Converter
CAO Feifei1), 2), 3), SHI Hongda1), 2), 3),*, LI Ming1), 2), 3), DONG Xiaochen1), and LI Demin1)
1) College of Engineering, Ocean University of China, Qingdao 266100, China 2) Shandong Provincial Key Laboratory of Ocean Engineering, Qingdao 266100, China 3) Qingdao Municipal Key Laboratory of Ocean Renewable Energy, Qingdao 266100, China
The heaving buoy wave energy device is popular for wave conditions with small wave heights and short periods. This paper presents the design of a wave energy converter composed of a gyro buoy, a hydraulic power take-off, and an electricity generation system. The energy accumulators are used to improve the output power with different control strategies. The quantity relations between each component are established using theoretical methods. The simulation model describes the energy conversion and calculates the operation time, energy capacity, and output power of the device under different initial pressures, release pressures, and electric resistances. As a result, the capacity is determined by the electronic load, and the maximum output power can be obtained when the accumulators are turned on and off at the same time. This study investigates the factors influencing the electric energy production and can be used to guide the optimization of this type of device.
wave energy; heaving buoy; power-take-off; accumulator; output power
1 Introduction
The energy from ocean waves is the most conspicuous form of ocean energy (Falcão, 2010). Wave energy devices have a wide variety depending on the different ways by which energy is converted, such as oscillating water column (OWC) type, overtopping type, and oscillating body (OB) type (Falnes, 2007; Borthwick, 2016; Babarit, 2017; Zhao, 2019). The overtopping wave energy converter (WEC) uses curved reflectors to gather sea water of incident waves into the central receiving part, where they flow up a ramp and over the top into a raised reservoir, from which the water is allowed to return to the sealow-head turbines (Drew, 2009). Overtopping WECs include TAPCHAN (Clément, 2002), Seawave Slot-Cone Generator (Vicinanza and Frigaard, 2008), and the Wave Dragon (Beels, 2010). The OWC WEC consists of a chamber with an opening to the sea below the waterline. As waves approach, water is forced into the chamber or return to the ocean, applying pressure on the air within the chamber. This air escapes to the atmosphere or drawn in the chamber through a turbine that drives an electrical generator (Morris-Thomas, 2007; Ning, 2016). OWC WECs include Limpet (Folley, 2006), Pico (Bruschi, 2019), Oceanlinx (López, 2013), and OE buoy (Khan, 2017). The OB WEC usually absorbs the wave energy by the motion of the bouy. The mechanical energy of the buoy is converted to a generator through a gear mechanism or hydraulic system. The OB-type WECs exploit powerful wave regimes available in deep water and have smaller size, which have become popular and develop rapidly in recent years, such as PowerBuoy (Edwards and Mekhiche, 2013), Wavebob (Schlemmer, 2011), Archimedes Wave Swing (Valério., 2007), CETO (Caljouw, 2011), Oyster (Babarit., 2012; Fadaeenejad., 2014), Salter’s Duck (Salter., 1976; Greenhow., 1982), and Pelamis (Czech and Bauer, 2012; Yemm., 2012). Laboratory experiments can provide convincing and useful data for designers and engineers (Choi., 2012; Lasa., 2012; Qu, 2015). Based on the validation of experimental data, the numerical model can realize the prediction from the incident wave energy to the output electric power directly. Most of these numerical models focus on the hydrodynamic performance of the heaving buoy under the effects of the power take-off (PTO) (Ma, 2013). However, few reports are available on the operating performance of the PTO (Liu., 2016).
The wave height is small, and the wave period is short in most parts of China sea (Shi., 2016). This paper presents an oscillating wave energy converter that is well applied to the above wave condition. Fig.1 shows a schematic of the oscillating wave energy converter. The device absorbs wave power by a gyro buoy and delivers the energy by the hydraulic system. It uses a double-acting hydraulic cylinder. The buoy moves up and down with waves and pumps oil into the accumulator to store energy. The oil is released out to drive the hydraulic motor when the internal pressure of the accumulator reaches the discharge pressure. The electricity generated by the synchronous alternator is transformed into direct current power with rectification and inverter control. Finally, the power is consumed by the resister. An experiment is carried out, and a numerical modeling of PTO is introduced to characterize the energy storage system and the converter.

Fig. 1 Schematic of the oscillating wave energy converter.
2 Experiment
A wave-to-wire experiment is conducted in the wave tank in Shandong Provincial Key Laboratory of Ocean En- gineering to investigate the performance characteristic of the PTO system.
The gravity similarity principle is applied in the wave model test, which means the Froude numbers of the prototype and the model are the same. In the PTO simulation, the wave force acted on the buoy is delivered by the cylinder and obeys the same scaling. In consideration of all the conditions, scaling is set to be 4:1. The tank scale is 60m´36m, the static depth is 1.5m, and a buoy with the draft of 0.1m is positioned 30m away from the wave generator. Regular waves are employed as incident waves with the wave heightvarying from 0.15m to 0.25m and the periodvarying from 1.65s to 1.90s. The upper part of the gyro buoy is a cylinder with a diameter of 0.9m and a height of 0.325m. The angle of cone at the bottom is 120˚. The mass of the gyro buoy is 80kg. The inside diameter of the hydraulic cylinder is 0.01m. The nominal volume of the gas accumulator is 1L, the initial pressure0varies from 1.50MPa to 2.10MPa, and the discharge pressure2is 3.25MPa. The displacement of the hydraulic motor is 8.2cm2r−1. The installed capacity of the generator is 50W. The model is shown in Fig.2.
3 Numerical Modeling
According to the physical characteristics and mechanics principle, the double-acting hydraulic cylinder, as shown in Fig.3, can be formulated as follows:
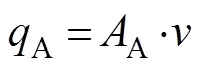


whereis the relative velocity of the cylinder rod;RandCare the absolute velocities of the cylinder rod and case, respectively;AandBare the piston areas at the sides without and with the rod, respectively;AandBare the pressures at the cylinder without and with the rod, respectively; andAandBare the flow rates through ports A (without rod) and B (with rod) from the cylinder, respectively.
The gas-charged accumulator, as shown in Fig.4, consists of a pre-charged gas chamber and a fluid chamber connected to the hydraulic system. It can be described with the following equations according to the Hydraulic Engineering Manual(Lei, 1998):



whereFis the volume of fluid in the accumulator,Ais the accumulator capacity,pris the volume of fluid at preload pressure,is the inlet gauge pressure,pris the preload pressure,ais the atmospheric pressure,sis the structural compliance of the accumulator inlet port structure,is the specific heat ratio, andis the volumetric flow rate.

Fig.2 Wave-to-wire experiment for the heaving buoy wave energy converter.

Fig.4 Model of the gas-charged accumulator.
The model uses a fixed-displacement hydraulic motor, which is represented with the following equations (Lei, 1998):



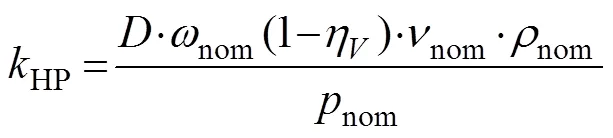


where ∆is the pressure differential across the motor,Cis the inlet pressure,Dis the outlet pressure,is the torque at the motor output shaft,is the motor displacement,is the output shaft angular velocity,leakis the leakage coefficient,HPis the Hagen-Poiseuille coefficient,ηis the motor volumetric efficiency,mechis the motor mechanical efficiency,is the fluid kinematic viscosity,is the fluid density,nomis the nominal fluid density,nomis the motor nominal pressure,nomis the motor nominal angular velocity,nomis the nominal fluid kinematic viscosity, andtotalis the total efficiency of the motor.
The model of the generator adopts the three-phase permanent magnet synchronous machine, which can be expressed by the following relations:



whereqanddare the q and d axis inductances, respectively;gis the resistance of the stator windings,qanddare the q and daxis currents, respectively;ris the angu-lar velocity of the rotor;qanddare the q and d axis voltages, respectively;gis the number of pole pairs;eis the electromagnetic torque; andis the amplitude of the flux induced by the permanent magnets of the rotor in the stator phases.
The resistor implements the relation

whereis the resistance,() represents the voltage across the terminals of the capacitor, and() represents the current.
On the basis of the above relations, the PTO system is simulated in SIMULINK, which is a powerful tool in Matlab fulfilling the task of this paper, as shown in Fig.5. The model takes the motion of the buoy as input data and the power as output.

Fig.5 Simulation model of the PTO system.
4 Simulation Results
For validation of the numerical modeling, the simulation results of the accumulator pressure, rotation speed of the motor, and output power are compared with the experimental data in Fig.6. Here,0=1.8MPa,2=3.25MPa,=0.25m, and=1.90s. Fig.6(a) shows that the simulated pressure curves for the charging and discharging processes are in good agreement with the experimental results. Under the hypothesis that time=0 when pressure in the accumulator reaches the discharging pressure in Figs.6(b) and 6(c), the rotation speed and output power for the numerical model are larger than the real results of the experiment. In addition, the motor and generator run slightly longer in the simulation model. The above differences might be caused by the hydraulic pressure loss in the pipes, and the gas in the liquid oil which causes the pressure in the test to be lower than that in the numerical model. In general, the numerical results agree well with the experimental results. Therefore, the simulation model can be used for the further study of the PTO system.
Under the same wave condition, the charging time is determined by the initial and the discharge pressure of the accumulator. However, the electric energy production of the wave energy converter is different from the resistance and the control strategy of the accumulators.
4.1 Optimum Resistance
The model adopts one accumulator, and the values of0and2are listed in Table 1. The resistance valuevaries from 5Ω to 25Ω. The electric energy production of the device obtained from the numerical model is shown in Fig.7. The power rises in the first stage and then decreases as the resistance increases. When the optimum resistance (hereR=15Ω) is used, the converter reaches the maximum generation. The smaller the resistance, the higher the reactive force is. It reduces the generator rotational speed, which lowers the output power. Conversely, the electric current decreases as the resistance increases, which decreases the output power.

Fig.6 Comparison of simulation and experimental data.
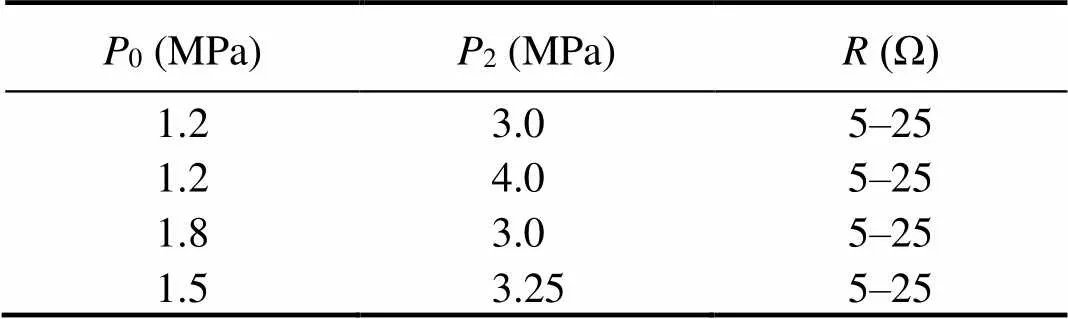
Table 1 Values of pressure and resistance
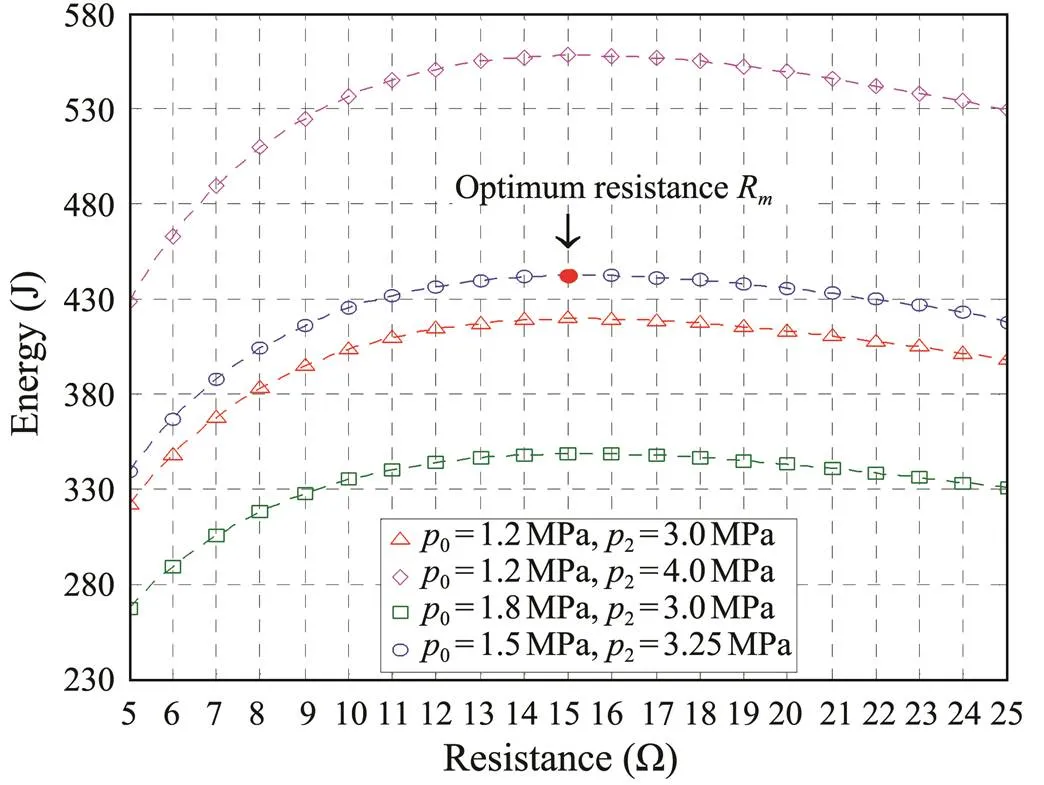
Fig.7 Electric energy production of the device.
4.2 Control Strategy of the Energy Storage System
The accumulators can be disposed in array to store more power in one process. The numerical model is established according to the operating principle of the energy storage system, as shown in Fig.8. Suppose that four accumulators are present in the energy storage and the nominal capacity of each is 2.5L. The pressure of the accumulator is monitored by the gauges. The electromagnetic ball valve switches under the pressure variation. The simulation presents three control strategies of the energy storage and analyzes the output power of the device under each case, as follows.
Strategy I controls the accumulators discharging in sequence. Electromagnetic ball valve 3-1 opens when the pressure in the accumulators reaches the discharge value, and the oil in accumulator 1-1 releases to drive the motor. Valve 3-2 opens when the pressure of the oil-way reduces to the initial value, and the oil in accumulator 1-2 releases. In the same way, accumulators 1-3 and 1-4 open to make the device produce electricity. All the valves turn off when the pressure in the accumulators falls to the initial value, and the energy storage system begins recharging.
Strategy II controls the accumulators discharging in pairs. When the pressure in the accumulators reaches the target level, charging stops. Accumulators 1-1 and 1-2 release the oil together when valves 3-1 and 3-2 open at the same time, so do the remaining pairs of accumulators.
Strategy III controls the accumulators discharging together when charging is finished.
On the basis of previous research, the output power of the device using different strategies with the optimum resistanceRis simulated. The initial pressure in each accumulator is 1.5MPa, and the discharging pressure is 3.25MPa. Fig.9 shows the time–history curves of the out- put power under three control strategies. By comparison, the generator works periodically when accumulators release the oil in turn or by pairs. The output is smooth when the valves open and close at the same time and the accumulators release the energy together. The output power of the device with a single accumulator whose nominal volume is equal to the four accumulators is also simulated.
The rotation speed of motor, voltage, current, output power, electric energy, discharge time, and average power are calculated using the numerical model (Table 2).
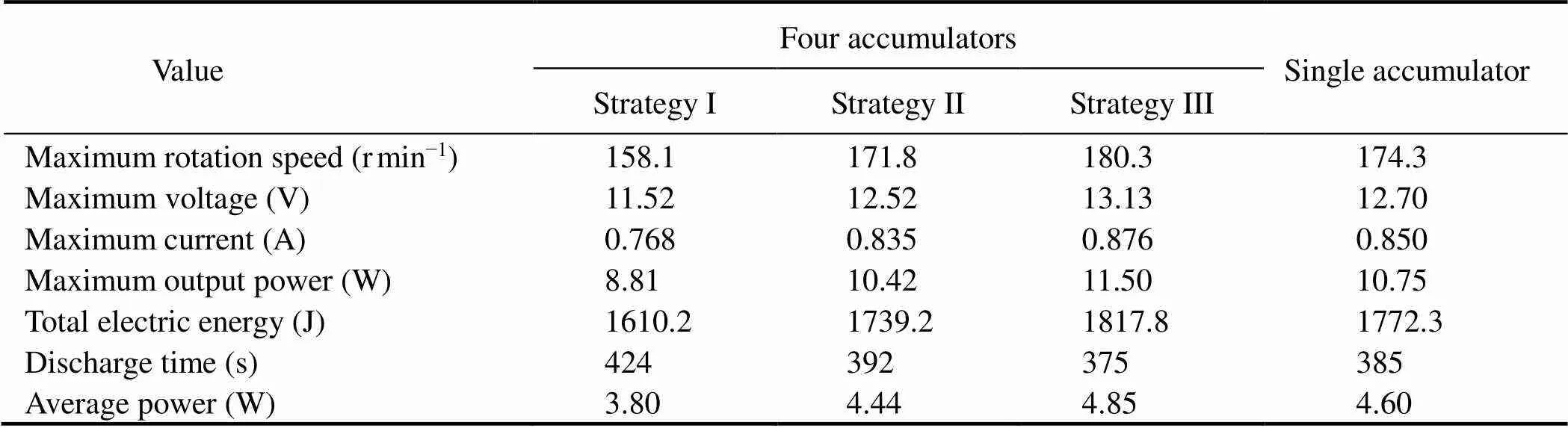
Table 2 Statistical chart under different strategies

Fig.8 Schematic of the energy storage system with multiple accumulators. 1, Accumulator, 2, Pressure sensor, 3, Electromagnetic ball valve, 4, Rate sensor, 5, Hydralic motor.

Fig.9 Time-history curves of the output power.
The above results show that strategy III is the best choice. The multiple accumulators arrayed in line under strategy III can meet the requirement of the storage, improve the output power, and increase the electricity output. Meanwhile, because of small size and flexible function, the accumulators are highly reliable and strongly adaptable.
4.3 Number of Accumulators
The number of accumulators is varied from one to ten and all the parameters are set the same as above to obtain the relation between the number of accumulators engaged in the energy storage and the power of the device. Fig.10 shows the output power of the generator.
Fig.11 shows that the maximum output power of the generator varies with the number of accumulators. The maximum value of the instantaneous power increases as the number of accumulators increases. However, the effect is weakened with the increase of such number.

Fig.10 Time-history curves of the output power of the generator.
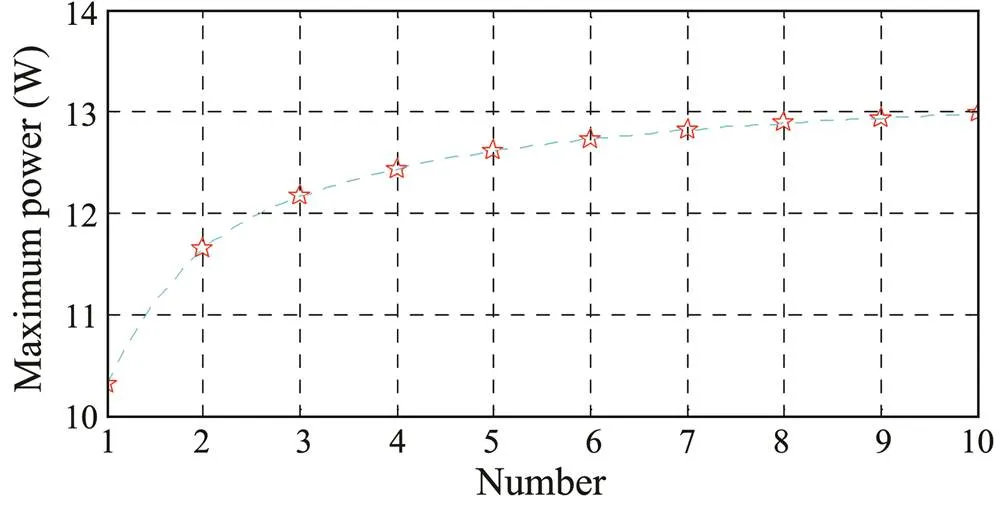
Fig.11 Maximum output power of the device with different numbers of accumulators.
The relation between electric energy and the number of accumulators is shown in Fig.12.
By the fitting calculation, the relation between electric energy and the number of accumulators is linear. The total energy of the device can be expressed as

where E represents the electric energy of the device with one accumulator and n is the number of accumulators.
5 Conclusions
The heaving buoy wave energy converter has simple form, which is flexible to be installed even in the deep sea. The study introduces this device with a hydraulic energy storage system and characterizes the PTO using a numerical method. With the increase in electric resistance, the efficiency of the energy conversion initially increases and then decreases. The maximum output power is obtained when the resistance value is optimized. When the converter is equipped with multiple accumulators, the electric energy reaches its maximum under the simultaneous discharge. The relation between electric energy and the number of accumulators is linear.
Acknowledgements
This work is sponsored by the National Natural Science Foundation of China (No. 41376100), the Shandong Provincial Natural Science Key Basic Program (No. ZR2017ZA0202), the Special Project for Marine Renewable Energy (No. GHME2016YY02), and the Shandong Provincial Key Laboratory of Ocean Engineering and Qingdao Municipal Key Laboratory of Ocean Renewable Energy.
Babarit, A., 2017.. ISTE Press-Elsevier, 99-153.
Babarit, A., Hals, J., Muliawan, M. J., Kurniawan, A., Moan, T., and Krokstad, J., 2012. Numerical benchmarking study of a selection of wave energy converters., 41: 44-63.
Beels, C., Troch, P., Visch, K. D., Kofoed, J. P., and Backer, G. D., 2010. Application of the time-dependent mild-slope equations for the simulation of wake effects in the lee of a farm of Wave Dragon wave energy converters., 35 (8): 1644-1661.
Borthwick, A. G. L., 2016. Marine renewable energy seascape., 2 (1): 69-78.
Bruschi, D. L., Fernandes, J. C. S., Falcão, A. F. O., and Bergmann, C. P., 2019. Analysis of the degradation in the Wells turbine blades of the Pico oscillating-water-column wave energy plant., 115: 109368.
Caljouw, R., Harrowfield, D., Mann, L., and Fievez, J., 2011. Testing and model evaluation of a scale CETO unit. In:. Southampton.
Choi, K. S., Yang, D. S., Park, S. Y., and Cho, B. H., 2012. Design and performance test of hydraulic PTO for wave energy converter., 13 (5): 795-801.
Clément, A., McCullen, P., Falcão, A., and Haider, A., 2002. Wave energy in Europe: Current status and perspectives., 6 (5): 405-431.
Czech, B., and Bauer, P., 2012. Wave energy converter concepts: Design challenges and classification., 6 (2): 4-16.
Drew, B., Plummer, A. R., and Sahinkaya, M. N., 2009. A review of wave energy converter technology. In:, 223 (8): 887-902.
Edwards, K., and Mekhiche, M., 2013. Ocean testing of a wave-capturing powerbuoy. In:. Washington.
Fadaeenejad, M., Shamsipour, R., Rokni, S. D., and Gomes, C., 2014. New approaches in harnessing wave energy: With special attention to small islands., 29: 345-354.
Falcão, A. F. D. O., 2010. Wave energy utilization: A review of the technologies., 14 (3):899-918.
Falnes, J., 2007. A review of wave-energy extraction., 20 (4): 185-201.
Folley, M., Curran, R., and Whittaker, T., 2006. Comparison of LIMPET contra-rotating wells turbine with theoretical and model test predictions., 33 (8-9): 1056-1069.
Greenhow, M., Vinje, T., Brevig, P., and Taylor, J., 1982. A theoretical and experimental study of the capsize of Salter’s duck in extreme waves., 118: 221-239.
Khan, N., Kalair, A., Abas, N., and Haider, A., 2017. Review of ocean tidal, wave and thermal energy technologies., 72: 590-604.
Lasa, J., Antolin, J. C., Angulo, C., Estensoro, P., Santos, M., and Ricci, P., 2012. Design, construction and testing of a hydraulic power take-off for wave energy converters., 5 (6): 2030-2052.
Lei, T., 1998.. Beijing Institute of Technology Press, Beijing, 311-313, 1770-1776 (in Chinese).
Liu, Z., Qu, N., Han, Z., Zhang, J., Zhang, S., Li, M., and Shi, H., 2016. Study on energy conversion and storage system for a prototype buoys-array wave energy converter., 34: 100-110.
López, I., Andreu, J., Ceballos, S., Alegría, I. M., and Kortabarria, I., 2013. Review of wave energy technologies and the necessary power-equipment., 27: 413-434.
Ma, Z., 2013. The study on hydrodynamic performance of oscillating floater buoy wave energy converter. PhD thesis. Ocean University of China.
Morris-Thomas, M. T., Irvin, R. J., and Thiagarajan, K. P., 2007. An investigation into the hydrodynamic efficiency of an oscillating water column., 129 (4): 273.
Ning, D. Z., Wang, R. Q., Zou, Q. P., and Teng, B., 2016. An experimental investigation of hydrodynamics of a fixed OWC Wave Energy Converter., 168: 636-648.
Qu, N., 2015. Study on hydrodynamic performance of oscillating buoy WEC considering power take-off system. Master thesis. Ocean University of China.
Salter, S. H., Jeffery, D. C., and Taylor, J. R. M., 1976. The architecture of nodding duck wave power generators., 1: 21-24.
Schlemmer, K., Fuchshumer, F., Böhmer, N., Costello, R., and Villegas, C., 2011. Design and control of a hydraulic power take-off for an axi-symmetric heaving point absorber. In:, Southampton.
Shi, H. D., Cao, F. F., Liu, Z., and Qu, N., 2016. Theoretical study on the power take-off estimation of heaving buoy wave energy converter., 86: 441-448.
Valério, D., Beirão, P., and da Costa, J. S., 2007. Optimisation of wave energy extraction with the Archimedes Wave Swing., 34 (17): 2330-2344.
Vicinanza, D., and Frigaard, P., 2008. Wave pressure acting on a seawave slot-cone generator., 55 (6): 553-568.
Yemm, R., Pizer, D., Retzler, C., and Henderson, R., 2012. Pelamis: Experience from concept to connection., 370 (1959): 365-380.
Zhao, X. L., Ning, D. Z., Zou, Q. P., Qiao, D. S., and Cai, S. Q., 2019. Hybrid floating breakwater-WEC system: A review., 186: 106-126.
. Tel: 0086-532-66781550
E-mail: hongda.shi@ouc.edu.cn
April 12, 2019;
December 23, 2019;
February 4, 2020
(Edited by Xie Jun)
杂志排行
Journal of Ocean University of China的其它文章
- Preparation of Clay/Biochar Composite Adsorption Particle and Performance for Ammonia Nitrogen Removal from Aqueous Solution
- Biochemical Factors Affecting the Quality of Products and the Technology of Processing Deep-Sea Fish,the Giant Grenadier Albatrossia pectoralis
- Study on Wave Added Resistance of a Deep-V Hybrid Monohull Based on Panel Method
- Air Temperature and Emersion Time Can Affect the Survival Rate and Ammonium Loading of Swimming Crab Portunus trituberculatus Exposed to Air
- Estimation of the Reflection of Internal Tides on a Slope
- Propulsion Performance of Spanwise Flexible Wing Using Unsteady Panel Method
