有限拓扑的编码算法*

2020-09-29陈建兵梁立叶志霞

云南师范大学学报（自然科学版） 2020年5期

关键词：数组二进制子集

陈建兵，梁立，叶志霞

(1.云南师范大学信息管理处,云南昆明650500；2.云南师范大学信息学院,云南昆明650500)

1 引言

对有限集合Xn={x1,x2,…,xn}的集族T，若满足下面两个条件：

(1)空集Ф和全集Xn都在T中(可行性)；

(2)对任意A,B∈T，都有A∩B∈T且A∪B∈T(封闭性);

则称集族T为Xn上的一个有限拓扑.

只由空集和全集组成的拓扑称为平庸拓扑，由全部子集组成的拓扑称为离散拓扑.如果拓扑T满足∪A∈T{Ф,Xn}A≠Xn,称T为Xn上的α拓扑.例如X={a,b,c}的离散拓扑是{Ф,{a},{b},{c},{a,b},{a,c},{b,c},X}；{Ф,{a},{b},{a,b},X}是X上的一个α拓扑.

有限拓扑的应用十分广泛，特别是在数据压缩和信息安全方面的应用[1].有限拓扑的数量相当庞大，给计算和存储带来压力[2]，因此有限拓扑的编码和压缩非常重要.

2 拓扑编码

用算法构建拓扑需要对拓扑进行编码，拓扑信息的存储也需要编码.拓扑的编码直接影响算法的时间复杂度和空间复杂度.因为有限集合的子集数是2n，所以容易想到用二进制数对其进行编码.拓扑编码的基础是集合的编码和集族的编码.

2.1 集合的编码

n元集合的表示方法有很多，最直接的方法是用长度为n的字符串或者字符数组表示，但字符串表示集合存在以下问题：一是占用的空间比较多，n元集合至少占用n个字节的空间；二是集合运算比较复杂，拓扑中主要是集合的“交”与“并”运算，集合的交运算需要求解类似“最长公共子序列”问题，集合的并运算除了字符串连接还需要字符串去重以保证集合中的元素唯一；三是集族的表示需要字符串数组(或二维字符数组).

虽然有些计算机语言(如Pascal和Python)有集合数据类型，但运算其实也是字符串的运算，仍然没有解决空间和时间的问题，而拓扑数据量的庞大必然需要追求存储空间少和计算速度快.

实际上，在拓扑运算中最关心的是n元集合的子集之间的运算，因为子集之间的“交”和“并”的运算比较频繁.

如果用一个n位二进制数xn-1xn-2…x1x0表示n元集合Xn的子集S:

则集合的运算就是二进制按位运算，运算简单且速度快，即

交集：A∩B=A&B

并集：A∪B=A|B

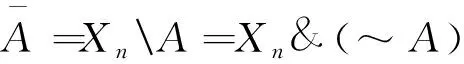
包含：A⊆S⟺A&S==A

例如，3元集合{a,b,c}的子集{a,b}=0112=3，{a,c}=1012=5，且

{a,b}∩{a,c}=011&101=001={a}

{a,b}∪{a,c}=011|101=111={a,b,c}{a,b}=111&(～011)=111&100=100={c}

这里～011可能得到的结果是11111100而不是100，所以必须跟Xn求“与”运算.

n元集合只需要n位二进制数，比n个字节的字符串所需存储空间至少少7倍(至少的意思是字符串还需要结束标志或者字符串的长度)，二进制数按位运算的速度快，而且自然“去重”保证了集合中的元素唯一.

集合的大小就是集合的编码数值.例如{a,b} < {a,c}.

2.2 集族的编码

n元集合的全部子集(包括空集和全集)有2n个，也就是离散拓扑的长度是2n.很容易想到用一个数组表示一个集族，但每一个集族的长度(基数)不一样，所以必须标记集族的长度或者集族之间的分隔符.用数组的第一个元素表示集族的长度比较方便.

例如，对3元集合{a,b,c}的一个集族{ {a},{b},{a,b},{a,c} }可表示为：

40012010201121012

用十进制数表示这个数组：

41235

下面这个数组表示了集合{a,b,c}的一个拓扑{Φ,{a},{b},{a,b},{a,c},{a,b,c} }：

6012357

因而集族{Φ,{a},{b},{a,b},{a,c},{a,b,c} }={0,1,2,3,5,7}.

这种方法对验证集族或拓扑的封闭性比较方便[3]，但是需要的存储空间比较大(每个元素的最大取值是2n-1).因为集族里的子集取值是0～2n-1间的连续整数，所以用2n位二进制数表示一个集族也是可以的.二进制的位置编号(从低位到高位编号0～2n-1)对应子集的十进制数，这就是占位编码.

例如上面例子中的集族{Ф,{a},{b},{a,b},{a,c},{a,b,c} }可以表示为23=8位二进制数：10101111(如表1)，也就是位置编号为0,1,2,3,5,7的二进制数为1，其余为0.

表1 二进制的位置编号

2.3 拓扑的编码

拓扑是特殊的集族.根据拓扑的可行性(拓扑中必须包含空集和全集)，每个拓扑都有空集和全集，所以拓扑的编码可以去掉空集和全集，只对其余2n-2个子集编码，因此可用2n-2位二进制数表示一个拓扑.

例如上面例子中的拓扑{Ф,{a},{b},{a,b},{a,c},{a,b,c} }可以表示为23-2=6位二进制数010111.虽然010111={1,2,3,5}不是一个拓扑，但在将它视为拓扑时，只需添加空集和全集就变成{0,1,2,3,5,7}.

因为二进制数的位置编号与拓扑中的子集一一对应，所以对二进制编码的拓扑解码也很容易.

3 拓扑编码算法

拓扑有两种表示，第一种是数组形式，主要用于计算；第二种是二进制形式，用于存储以节省空间;因此，把计算结果用于存储时需要把第一种形式变成第二种形式，这个过程是拓扑的编码；需要计算时取出第二种形式的二进制数据变成第一种形式的数组，这是解码.

因为绝大多数拓扑中的子集是比较稀疏的，也就是拓扑的二进制数中0比较多，因此，为了节约存储空间，可把二进制数进行压缩.

3.1 拓扑编码算法

拓扑编码算法：把数组表示的拓扑T编码为二进制表示的拓扑TB.

输入：数组T.//T[0]表示拓扑的长度，T[1]表示空集，T[T[0]]表示全集

对k从2到T[0]-1，做

x=T[k]; // 取一个子集在二进制里的占位编号

i=(x-1) / 8; // 在第几个字节

j=(x-1)x%8; // 在字节内的占位编号

TB[i] = (1<

输出：数组TB.//数组TB的类型是字节，长度是2n-3.

例如n=5时，Xn={a,b,c,d,e}

拓扑：{ Φ,{a},{a,d},{a,b,d},{a,e},{a,d,e},{a,b,d,e},{a,b,c,d,e} }

输入数组T：{ 8,0,1,9,11,17,25,27,31 }//8是数组的长度

输出数组TB： 00000001 00000101 00000001 00000101

第0字节：00000001(表示子集1={a})

第1字节：00000101(表示子集9={a,d},11={a,b,d})

第2字节：00000001(表示子集17={a,e})

第3字节：00000101(表示子集25={a,d,e}，27={a,b,d,e})

输出数组TB中并不包含空集和全集，因为每一个拓扑都包含空集和全集.输出数组TB不需要记数组的长度，因为它们的长度都一样(2n-3).

可以看出，数组表示需要9个字节，二进制表示需要4个字节，二进制表示1的个数就是拓扑的长度(不含空集与全集).从上例还看到拓扑中1的数量很少，因此，拓扑的二进制形式很稀疏(0很多)，有利于数据压缩.

3.2 拓扑解码算法

拓扑解码算法：把二进制表示的拓扑TB解码为数组表示的拓扑T.

输入：数组TB.//共有bytes=2n-3个元素的字节数组(当n≤3时bytes=1)

初值j=2;

对 i 从0到bytes-1，做：//对第i个字节处理

x = TB[i];

k = 8 * i;

对y从1到8，做: //y是在字节内的占位编号

如果x&1 ≠0，则T[j++]= k+y; //1的位置k+y是子集的编号

x >>=1;

T[0]=j; //拓扑长度

T[1]=0; //空集

T[j]=2n-1; //全集

输出：数组T.//T中元素的最大取值2n-1.

输入数组TB不包含空集和全集，所以输出数组T需要添加空集和全集并计入数组长度.

例如n=5时，Xn={a,b,c,d,e}.

输入数组TB：00000001 00000101 00000001 00000101

第0字节：00000001(表示子集1={a})

第1字节：00000101(表示子集9={a,d},11={a,b,d})

第2字节：00000001(表示子集17={a,e})

第3字节：00000101(表示子集25={a,d,e}，27={a,b,d,e})

输出数组T：{ 8,0,1,9,11,17,25,27,31 }

需要说明的是，二进制数组TB原本是一个长数据，应该从低字节到高字节从右向左排列，但程序设计时用到数组元素下标从0开始由左向右；另外，TB习惯上看见的是十进制数，比如上面的TB={1,5,1,5}，视为4字节的长数据的二进制数是00000101 00000001 00000101 00000001(十六进制数是05010501)，它的十进制数是83952897.所以，相当于用十进制数83952897表示了拓扑{ Φ,{a},{a,d},{a,b,d},{a,e},{a,d,e},{a,b,d,e},{a,b,c,d,e} }.但是，当n越来越大时(如n≥7)，没有任何一种编程语言能表示2n-2位这样大的整数类型，即使64位的编程语言也只能取到n=6，所以就用字节数组来组装这个拓扑二进制数.