基于小学数学开放题学习的思辨能力
2020-09-28杨传冈

摘 要: 小学是学生思辨能力发展的启蒙期,亦是习惯养成期。就学科特质而言,在小学数学学习过程中发展学生的思辨能力具有先天的优势。“解题”是一种最基本的数学活动形式,数学开放题在题型特点、解题思路、问题答案等方面呈现出来的特征对发展学生的思辨能力具有独特优势。用好开放题资源有助于发展学生的高阶思维能力。
关键词:小学数学;开放题;思辨能力
思辨能力是指“个人为了决定某物的真实价值,运用恰当的评价标准进行有意识的思考,最终做出有理据的判断的能力”。近年来,思辨能力一直是西方学术界研究的热点之一,国内研究也正处于发酵期,当前不断涌现对小学生思辨能力现状的反思,越来越多的教育工作者开始尝试、探讨小学生思辨能力的培养与发展。就学科特质而言,在小学数学学习过程中发展学生的思辨能力具有先天的优势,本文尝试从小学数学开放题学习这个视角来阐释笔者的点滴思考。
一、数学思辨能力的理解与把握
就目前而言,对数学思辨能力的认知和理解处于多元状态,较为典型的有三种:一是从“思考”和“辨析”视角,二是从问题解决视角,三是从思辨发生的心理过程视角。从“思考”和“辨析”的二维视角来说,数学思辨能力是一种综合性的数学思维能力,涉及数学思考、分析、推理、判断、表述、交流等数学思维过程和活动;从问题解决的视角来说,数学思辨就是让学生从数学的角度观察问题、分析问题、思考问题并解决问题,逐步提高学生的数学素养;从思辨发生的心理过程来说,思辨能力是指一种站在宏观的、抽象的、客观的角度推演事物的能力,它是从高度抽象的视角运用逻辑思维来判断事物的能力。
笔者以为数学思辨能力是一种高阶思维能力,即通过数学眼光观察分析,用数学思维思考辨析,用数学语言抽象表达,在探寻问题解决过程中所形成的集分析、辨别、推演、反思、建模于一体的综合能力。从本质上说,数学思辨能力是一种抽象思维能力,是一种较高层次的批判性学习力。和其他思维能力不同的是,数学思辨能力更强调内在的思考、自觉的外显表达,着重对数学问题有条理地进行剥笋式的解构分析,形成问题解决方案,及时反思、检查解题方案的合理性、科学性、完整性,在大脑中主动建构模型,在瓜熟蒂落之时自然流淌出思考的心声,留下思维的印痕。
二、数学思辨能力与开放题学习
小学生接触到的数学学习资源绝大部分都是条件与问题存在唯一对应关系的数学问题,也就是传统意义上的封闭问题。大量的课堂教学现场观察及对师生的访谈均显示:随着学段的升高,小学生的思辨能力并没有得到显著提升。具体表现为:面对新问题时解题意愿不足,解题态度慵懒懈怠,解题思路混沌茫然等。显然,这和时代发展对高素养人才的需求不相匹配。
具有较强思辨能力的学生一般表现出勇于嘗试、积极思考、思路清晰、善于反思等外显特征。数学开放题是一种“答案不唯一,并在设问方式上要求学生进行多方面、多角度和多层次探索的数学问题”。一方面,开放题独特的题型特征有利于发展学生的思辨能力;另一方面,学生思辨能力的强弱直接决定其开放题问题解决的能力水平。两者相辅相成,互相影响,互相促进。从这个意义上来说,小学数学开放题学习能够有效补齐学生思辨能力发展不足的短板。
三、开放题学习的思辨模型框架
20世纪80年代,美国哲学协会“特尔斐”项目组提出:思辨能力包括阐释、分析、评价、推理、解释以及自我调节,其中分析、推理与评价为核心技能。美国哲学家Bichard Paul和教育心理学家Linda Elder基于教学需求提出思辨三元结构模型:思维元素、标准和智力特征。我国学者文秋芳提出了思辨能力层级理论模型(见表1),将元思辨能力和思辨能力置于上下层关系,突出思维者的主观能动性在高层次思维中的主导作用,从而凸显思辨者的元思辨能力,以提高思辨者的主观能动性。
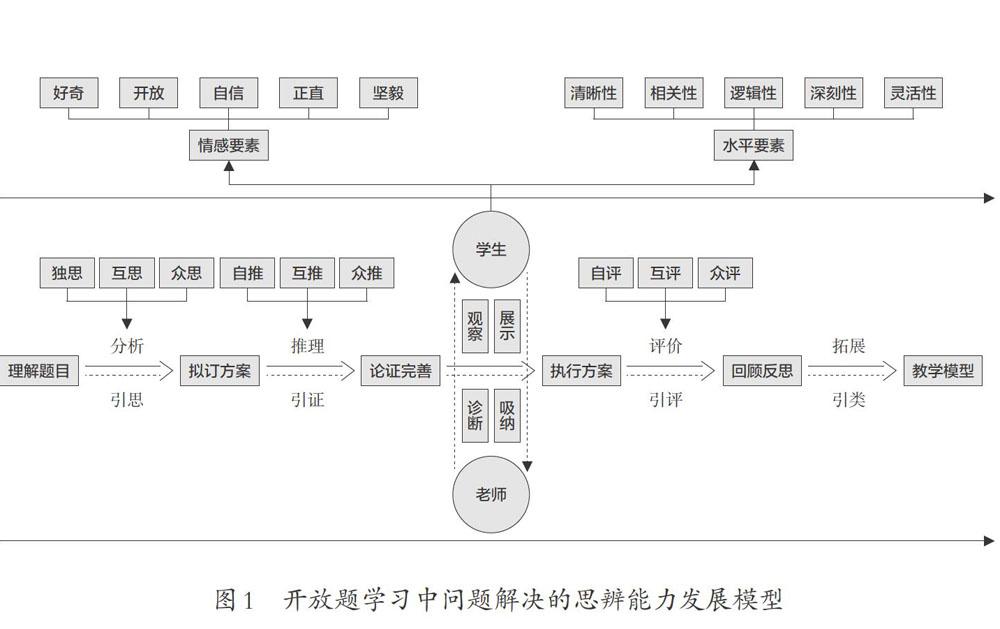
小学阶段不仅是学生思辨能力发展的启蒙期,也是学生思辨能力的养成期。小学生思辨能力培养发展的载体、路径众多,而基于数学开放题学习是一个全新话题。如果能建构初步的模型结构(图1),不仅有助于后续研究的深入,还有助于教师整体把握学习资源,精致备课,精心预设,根据学生学习状态及时调整课堂教学行为,给学生更自由的思考和辨析机会、更充足的自学和互学时空,满足学生思辨能力的发展需求。根据思辨能力层级模型结构,我们解剖开放题学习中问题解决的过程,将学生思辨能力的要素进行细化,充分凸显学生的主体地位,发挥教师引思、引证、引评、引类的辅助学习作用,通过教师对学生思、辨、评、类的观察、分析及课堂教学的及时矫正,促进学生思辨能力向纵深发展。
四、开放题学习的思辨能力培养
(一)发展学生多向度的分析能力
经过大量封闭习题的训练,学生对同一类型问题的熟悉程度逐渐增强,通过强化记忆达到了熟练化甚至自动化,但令人遗憾的是学生思维愈发固化,分析能力也未得到显著提升。数学开放题学习首先要打破学生的思维定式,因为提供的条件和所求问题之间并不存在必然的唯一联系,要想解决实际问题就需要学生从多方面入手、多角度思考、多层次探索,对题目已有信息进行梳理、分析、匹配、关联,想方设法挖掘条件和问题之间存在的各种可能的联系,不放过任何蛛丝马迹,尽可能发散自己的思维,将已知信息排列、整合、优化、重组,进行大胆的猜想,并提出初步的解决方案。
在这个过程中,学生可以独立思考,遇到困难可以在独立思考的基础上进行小组交流,启发新的思考,也可以通过学生的思维风暴,让问题解决思路更明确、方案更具体,课堂互动带领学生思考、促进互学互思,汲取众人思考的精华,触发自己思维的再深入。事实上,在开放题学习过程中,能独立、完整解决问题的学生较少,往往需要借助小组乃至全班学生的智慧共享。长此以往,学生面对一个新的问题时,大脑皮层中涌现出的将不再是一条路径,而是更多、更合理的可能路径,从而为学生分析能力的发展提供了广阔的实战场。
(二)发展学生有条理的推理能力
推理能力是学生问题解决的关键能力,教师在课堂学习中可着力糾正学生思维的随意性,引导学生养成规范性思维,发展学生有序推理能力。开放题与封闭题解题思路不同,在经过一段时间训练后,多数学生能根据题意提出不同解题设想。这些设想是否切实可行,能否转化为现实,往往需要进行多路径分析、论证、推理;另一方面,面对众多解决预案,学生需要合理筛选、分类、归并,进行有序推理,避开思维误区,通过更深入的思考快捷地做出判断,剔除无效路径,跟进有效预案。在这个过程中,教师要倡导、鼓励学生对自己的预想进行独立性批判,有顺序、有条理地进行合理性推理、论证,明确解决目标,指引解题方向,整合解决预案,完善并形成较为完整的解决方案。对学习有难度、思考有困难的学生及小组,教师要及时组织研究性学习及交流,正所谓“水尝无华,相荡乃成涟漪;石本无火,相击而发灵光”。
(三)发展学生多样化的表达能力
数学开放题一方面为不同水平学生的学习提供了问题解决的机会,人人都能解决问题;另一方面也在无形中增加了获得全部答案的思维难度。为了让更多学生在思维能力上有更显著的提升,教师要重视学生表达能力的培养。表达能力不仅包括口头语言表达能力,还包括文字表达能力、数字表达能力、图示表达能力,其中数字表达能力、图示表达能力尤须重视。让学生用数学的方式呈现问题思考的过程,再用数学语言表达出来,有助于培养学生的抽象思维能力。
数学思维的正确传达是思辨能力的重要一环,清晰的解题思路是解决数学问题的关键。教师通过不同层级学生的多种形式表达,让学生把对问题解决路径的大胆猜想、对问题可能方案的大胆构思、对问题解决路径的推理论证等清晰地展示出来,实现思维的可视化,这样做不仅可以抛砖引玉,启发他人思考、评判、碰撞,生发新的思考,也可以作为错误资源供他人参考,避免走思维弯路。有利于教师及时洞悉学生的所思所想、所悟所误,从而有效把控课堂。
(四)发展学生有深度的辨析能力
辨析能力的高低是学生数学思辨能力强弱最显著的标志。从思辨过程看,解决开放题问题教师应重点关注学生辨析能力发展的三个层面:一是学生个体内在的思考与自辨,二是学生之间的互动思考与互辨,三是学生与教师之间相互的启迪与众辨,其中学生个体内在的思辨尤为关键。“话不说不透,理不辩不明。”充分的辨析能够挖掘字面以外的信息,从无关联的信息中找到联系,从纷繁的信息中拟定预案,从众多可能的方案中做出判断;充分的辨析能培养学生的数学素养,对问题答案的正确性及全面性做出全方位评估,活化思维,提升能力。教师要做的就是想方设法给予学生思考、辨析和反思的充分“时空”,及时提供技术、智慧、平台的支持,并根据学生的实际表现适切地调整学习进程,引思促辨,以辨促思。
(五)发展学生多维度的情感能力
数学新课程改革的一个重要育人目标就是要有效促进学生良好情感态度价值观的形成,数学开放题学习能较好地实现这一目标。数学开放题在题型特点、解题思路、问题答案等方面呈现出的特征具有较好的育人价值,这种价值在“新数运动”后已成为人们的共识:开放题是最具教育价值的一种习题类型。培养学生思辨能力的价值体现在以下几个方面。
首先,开放题能满足学生的好奇心,吸引学生集中智慧、想方设法获得问题答案,让因材施教成为可能;其次,在教师的引导帮助下,学生逐步学会独立面对问题,深思熟虑地解决问题,并能积极参与团队合作,开展研究性学习,善于表达自己的观点,勇于坚持正确的主张,倾听、容忍、尊重、接纳不同的见解,乐于修正自己的不当观点,逐渐把开放包容内化为一种习惯、一种态度;最后,开放题问题解决中存在的种种不确定性,在一定程度上加大了学生的认知负荷,提高了学习难度。这既是挑战,又是机遇。
总之,逻辑分析的思辨并不代表全部数学,但它使我们对数学事实和它们相互间的依赖关系有更深刻的理解,以及对数学中的概念有更深刻的理解。数学开放题学习有助于发展学生的思辨能力,教师教给学生的是思辨方法,学生自悟并应用思辨方法。学生自己探寻思辨的方向,遇到困难时,教师可以启发学生思辨方向。教学中,教师给足学生思考、反思的时间,让学生用心琢磨,细致推理,精于表达,善于辨析,相信学生的思辨能力可以往前再进一大步。
参考文献
[1]戚洪祥.数学教学中培养学生思辨能力的研究述评[J].江苏教育研究,2019(25):52-56.
[2]宫玉荣.数学文化与大学生思辨能力的培养[J].数学学习与研究,2012(19):14-15.
[3]文秋芳,王建卿,赵彩然,刘艳萍,王海妹.构建我国外语类大学生思辨能力量具的理论框架[J].外语界,2009(1):37-43.
[4]杨传冈.小学数学开放题问题解决的价值定位、模型与思考[J].新课程研究(上旬刊),2016(1):45-47.
[5]杨传冈.小学数学开放题教学行思[J].教育探索,2015(11):31-35.
