基于条件特征函数和蒙特卡洛模拟的可赎回债券定价
2020-09-28吴依李小飞长江大学信息与数学学院湖北荆州434023
吴依,李小飞 (长江大学信息与数学学院,湖北 荆州 434023)
债券是一种按一定利率对债券持有者支付股息并按约定条件偿还本金的债权债务凭证,属于有价证券。作为一种债券债务凭证,债券被应用在与保险结合共同抵抗人身安全和财产风险[1~3]、与信用等级结合共担公司违约风险[4~6]等领域。不支付股息并以贴现方式发行的债券称为零息票债券,按照票面进行打折出售,到期时利息和购买价格之和即为债券的面值。可赎回债券赋予债券发行者在赎回日以事先约定的价格从债券持有者手中回购债券的权利,因此可赎回债券通常被视为嵌入了欧式期权或百慕大期权的债券[7]:如果赎回日唯一,称为欧式可赎回债券;如果存在多个赎回日,称为百慕大可赎回债券。
对于欧式可赎回债券,由于赎回日固定,其定价原理相对简单[8~10];对于百慕大及其他类型的可赎回债券,其定价原理相对复杂,且实际交易中主要以该类债券为主,受到许多学者的关注[11~14]。鉴于百慕大可赎回债券在实际金融市场的交易活跃性和实用性,笔者从定价原理出发,利用条件特征函数并结合蒙特卡洛模拟方法推导出百慕大可赎回债券的定价公式,并利用数值试验进行了验证。
1 条件期望的逼近
对金融产品定价的一个难点在于计算条件期望,国内外有许多学者做过研究[15~17]。最近,Ding等[18]利用一维傅里叶级数展开的方法,结合倒向随机微分方程,得到了一种利用正倒向随机微分方程确定的期权定价公式。该公式利用了标的资产的特征函数来对条件期望进行估计,并证明了误差可控,且结果精度高。
设标的资产X(t):0≤t≤T服从随机微分方程(SDE):
(1)
式中:W(t)为标准布朗运动;μ(x)和σ(x)满足李普希兹条件和线性增长条件。
给定时间[0,T]的一个分割Δ:0=t0<… 引理1[18]设φ(w|x)为条件密度函数p(y|x)的条件特征函数,对合适的正整数N,有: 说明选择合适的项数N后,可以利用条件特征函数来对条件期望进行估计,并通过最小二乘蒙特卡洛模拟法计算出条件特征函数的系数项。 债券和其他金融产品一样,其价格依赖于利率的走势,具有一定的风险,因此其定价显得比较重要,这就需要对利率过程进行精细描述。利率过程通常可用随机微分方程表示,常用的利率模型有Vasicek模型、Brennan-Schwartz模型、Marsh-Rosenfeld模型、Cox-Ingersoll-Ross(CIR)模型等。其中,CIR模型运用最为广泛,在对零息票债券、欧式债券、百慕大债券等债券进行定价时通常采用CIR模型。CIR模型为均值回归平方根模型,保证了利率过程非负,且很好地描述了利率的变化趋势。鉴于CIR模型的优点,笔者考虑CIR模型下的百慕大可赎回债券定价。 假设利率过程r(t)服从随机微分方程: (2) 式中:κ,θ,σ,r0为正常数。 式中:参数满足4κθ>σ2。 主要考虑一类利率过程服从CIR模型的百慕大可赎回债券的定价问题。百慕大可赎回债券通常有一个锁定期,在锁定期内发行者禁止赎回债券,过了锁定期方可赎回债券。在每一个赎回日前通常有一个公告日,在这个公告日债券发行者要决定是否赎回债券,设置公告日是为了保护债券发行者避免或者抵御债券价值出现重大变化。由于可赎回债券不同于定息债券,因此其价格依赖于嵌入的期权价格,这导致了百慕大可赎回债券定价的复杂性。对于百慕大可赎回债券,目前有许多定价方法,如二叉树方法、偏微分方程方法、蒙特卡洛模拟法等。Buttler[23]利用有限差分和带边界格式的算法确定自由违约折扣下百慕大可赎回债券的价格,Bliss等[24]指出最优的赎回政策并非在赎回价达到时便立即赎回。下面笔者利用条件特征函数推导定价公式。 假设瞬时利率r(t)服从随机微分方程(2),则条件特征函数为: 到期日为T的零息票债券在当前时刻t的价值为: Z(t,T;rt)=eA(t,T)-B(t,T)rt 假设在付息日Ti债券持有者得到的票息流为cTi(i=1,…,I-1),记TI,…,TL表示赎回日,KI,…,KL表示敲定价格。在每一个赎回日TI,…,TL,债券发行者需决定是否赎回债券并支付债券持有者KI,…,KL,或者让债券持有者继续持有直至下一个赎回日。考虑公告日发生在赎回日前δ,即Ti-δ,在公告日Ti-δ,当连续付息价值CTi-δ大于敲定价格Ki的折现值时,理性的债券发行者会选择赎回债券,因此,公告日Ti-δ时刻该债券的价值可以表示为: VTi-δ(rTi-δ)=min{Z(0,δ;rTi-δ)Ki,CTi-δ(rTi-δ)}+Z(0,δ;rTi-δ)cTi 债券的价值VTi-δ(rTi-δ)可以由倒向归纳法给出:在到期日T,设置VT(rT)=1+cT表示在到期日T前债券未被赎回时的价值;在时刻Ti-1-δ,继续持有债券的价值可以表示为: (3) 由于赎回日在敲出期TI及之后,因此可赎回债券的初始价格为: (4) 从式(4)可以看出,为了求出初始值,关键问题就是求出CTi-1-δ(rTi-1-δ),即确定式(4)的条件期望,因此可以选用条件特征函数进行处理,步骤如下: 步1设置离散步长h,h可以根据实际需要进行设置,如月、天等; 步3给定利率初值r0,利用Matlab随机模拟N条利率过程; 步5在每一个执行赎回日期i(I≤i≤L),进行如下操作: 1)对每一条离散路径n,利用最小二乘法计算时刻τi-d的持有函数: 3)在i=I时停止,计算第1个公告日时刻Ti=δ=(τI-d)h的折现价值: 并计算初始时刻可赎回债券的价格: TI=T11=11,…,TL=T21=T=21 相应的敲定价格为: K11=1.025K12=1.020K13=1.015 K14=1.010K15=1.005K16=…=K21=1 CIR模型参数为: κ=0.54958046θ=0.38757496σ=0.0348468515r0=0.0752280589 容易验证随机微分方程(2)有正解。随机生成5000条利率过程(N=5000),计算该债券的初始价格,并比较笔者的数值解与Buttler[26]数值解的误差(文献[26]中利用PDE方法结合Green函数计算出的数值解为0.7981)。 表1 不同M和h的百慕大可赎回债券的价格 作为金融领域的一种重要产品,债券的定价问题一直以来都是金融计算方法中一个热门话题,债券的价格因市场利率而变使得债券定价问题变得很复杂。笔者考虑了一类市场利率服从CIR模型的可赎回债券的定价问题,利用条件特征函数近似逼近一类条件数学期望,结合最小二乘蒙特卡洛方法,得到了该类债券的定价公式,最后通过数值模拟检验了该定价公式的效果,与经典的偏微分方程数值解的结果进行了对比,验证了该定价模型的可行性。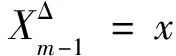
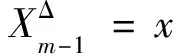
2 CIR利率模型
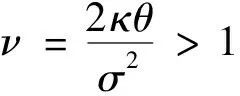
3 百慕大可赎回债券定价
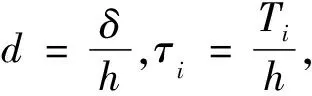
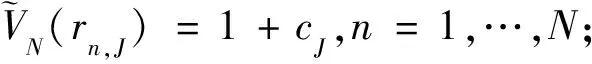
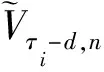
4 数值模拟
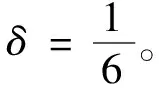


5 结语
