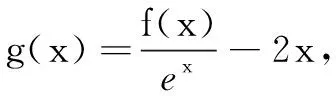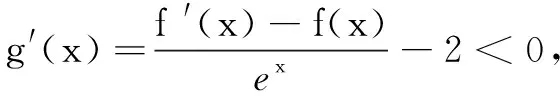例谈解决函数压轴题的化归与转化维度
2020-09-27江宝龙
江宝龙
(内蒙古乌兰浩特一中,137400)
本文例说如何运用化归与转化的方法多维度解决函数压轴题.兹将诸维度介绍如下.
一、 结构转化
对于函数压轴小题,题设中往往出现一些难以突破的结构,要求学生能根据已有解题经验对题设中的结构特征进行识别和深加工,将结构转化成已知问题,突破结构特征的难点,实现将未知问题转化已知问题的目的,进而问题得以解决.
例1若lnx1-x1-y1+2=0,x2+2y2-4-2ln 2=0,则(x1-x2)2+(y1-y2)2的最小值为______,此时x2=______.
解设A(x1,y1),B(x2,y2),则点A在曲线y=lnx-x+2上,点B在直线l:x+2y-4-2lnx=0上,问题等价于求A,B两点间距离的平方的最小值及相应点B的横坐标.

由切点到直线l的距离
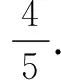

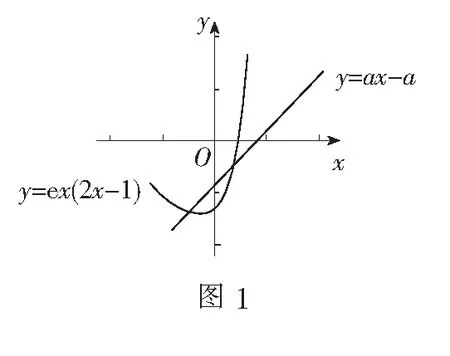
变式已知变量x1,x2∈(0,m),且x1 [ : e] 1.方程的根、函数的零点、图象的交点相互转化 函数的零点问题一直是高考的热点问题,其解决问题的核心为:函数y=f(x)-g(x)有零点⟺方程f(x)=g(x)有实数根⟺函数y=f(x)与y=g(x)图象有交点. 例2已知函数 若函数y=f(f(x)-a)-1有三个零点,则实数a的取值范围是( ) 解由f(f(x)-a)-1=0,得f(f(x)-a)=1,又易知方程f(x)=1的根为x=-2或x=0,问题等价于f(x)-a=-2和f(x)-a=0共有三个根,即方程f(x)=a和f(x)=a-2共有三个根. 解得1 2.量词“任意”和“存在”相关问题的转化 有关量词“任意性”、“存在性”的问题也是高考命题的热点问题,把函数问题、导数问题和不等式恒成立问题交汇命制压轴题已成为热点命题方向.其中确定参数取值范围问题,常用分离参数、 数形结合、参数讨论等方法,借助函数的最值与值域解决问题. 例3设函数f(x)=ex(x-1),g(x)=mx-m(m>0),若对任意的x1∈[-2,2],总存在x2∈[-2,2],使得f(x1)=g(x2),则实数m的取值范围是( ) 分析本题求解的关键是弄清题设中“任意性”与“存在性”的关系,明确在区间[-2,2]上,f(x)的值域是g(x)的值域的子集. [参考答案:[1,+∞)] 华罗庚先生曾说过:"数形结合百般好,隔裂分家万事休."数形结合是处理函数问题的常用思想方法,通过"以形助数"或"以数解形",可以使复杂问题简单化,抽象问题具体化,从而实现优化解题途径的目的. 例4设函数f(x)=ex(2x-1)-ax+a,其中a<1,若存在唯一的整数x0,使得f(x0)<0,则实数a的取值范围是( ) 解设g(x)=ex(2x-1),由题意知y=g(x)位于直线y=ax-a下方的图象(如图1)中只有一个点的横坐标为整数. 函数问题具有抽象性和具体性的双重特点.对抽象函数问题,把握其结构特征,透过结构看本质,能使抽象问题具体化,通过对具体问题的研究,实现问题的解决. (A)(-∞,1) (B)(1,+∞) (C)(-∞,2) (D)(2,+∞) (C)[0,+∞) (D)(-∞,0] [参考答案:选B]二、设问方式转化
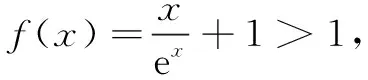
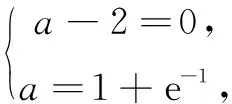
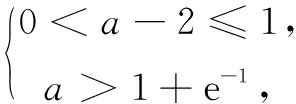

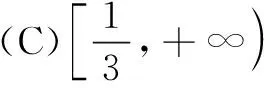
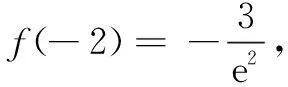

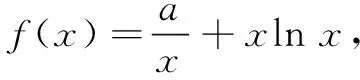
三、数与形的转化
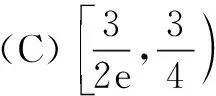
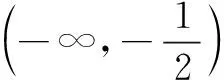
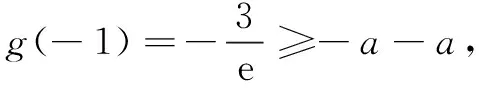
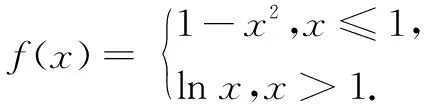
四、抽象到具体的转化