基于新进化优化BP学习算法的心音识别方法
2020-09-27袁倩影全海燕
袁倩影, 全海燕
(昆明理工大学 信息工程与自动化学院, 昆明 650504)
心音是由于心脏活动而产生的一种振动信号, 心音信号的识别有利于对心血管类疾病的诊断. 目前, 对心音信号进行特征提取的方法已有很多[1], 如Fourier变换、 小波分析、 Hilbert变换等方法. Fourier变换和小波分析均易导致相位信息的丢失, 影响后续分类器的设计[2]; Hilbert变换可处理非静态、 非线性的特性, 适合应用于突变信号[3]. 心音信号分类器主要采取支持向量机、K近邻、 神经网络等算法进行构建[4]. 支持向量机可通过多分类器的构建处理有关多分类的问题, 但训练时耗较长, 核函数的选取较复杂; 基于遗传(GA)算法等改进BP神经网络的学习算法可作为心音分类器, 但都是以增加算法控制参数和迭代次数为代价提高心音识别率. 基于此, 本文提出一种基于单形进化优化BP神经网络学习算法的心音识别方法, 对比实验结果表明, 该方法提高了心音分析的识别率, 可为心血管类疾病的诊断提供技术支持.
1 基于FastPCA的心音信号特征提取
主成分分析(PCA)是通过线性变换将源数据变换为一组各维度线性无关数据的统计分析方法. 计算主成分的目的是将高维数据投影到低维空间, 通常用于对高维数据空间的降维. 传统PCA步骤如下:
1) 对样本x去均值化得到向量Z;
2) 对向量Z求协方差系数Sl=ZTZ∈d×d, 其中d为样本x的维数;
3) 求解协方差Sl的特征值D和特征向量V, 特征值D即为样本x的主成分;
4) 将D按数值大小排列, 计算累计贡献率;
5) 根据累计贡献率大小确定第1、 第2、 …、 第k个主成分[5]. 一般根据累计贡献率在85%~95%内选取主成分的维数.
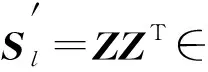
2 基于SSSE算法优化的BP神经网络
2.1 BP神经网络
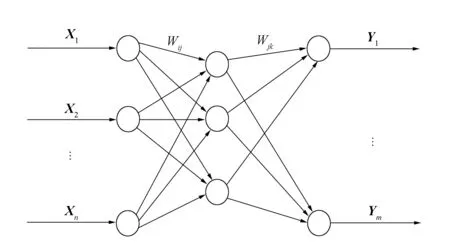
图1 BP神经网络结构Fig.1 Structure of BP neural network
BP神经网络是一种按误差逆传播算法训练的多层前馈网络, 应用广泛. BP神经网络的结构一般由输入层、 隐含层和输出层构成[7], 其网络结构如图1所示, 其中Xi(i=1,2,…,n)表示输入向量;Wij和Wjk表示权值;Yk(k=1,2,…,m)表示输出向量. BP神经网络中的神经元采用Sigmoid(S)函数做为激励函数, 且在网络中每层神经元的结果都与上一层神经元的处理结果有关. 由图1可见, BP神经网络采用三层结构, 输入层神经元数目为i=1,2,…,n, 隐含层单元个数为j, 输出层神经元数目为k=1,2,…,m.
BP神经网络学习算法的核心是优化BP神经网络输出与期望的误差函数, 本文采用误差绝对值, BP神经网络的误差函数定义为
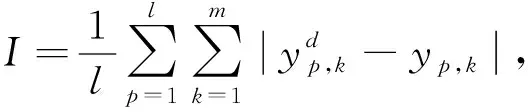
(1)
目前, 已有许多改进BP神经网络智能优化算法[8], 例如: 基于遗传算法的BP神经网络, 缺陷是遗传算法对种群数量和变异的编码长度选取要求极高; 基于粒子群优化算法的BP神经网络, 优点是参数较少, 但在求解过程临近结束时, 初始设置的粒子通常会聚集在某极值附近, 粒子寻优过程较慢, 直接导致增加了收敛时长和偏差. 这些改进的BP神经网络智能优化算法常通过设置更多的参数, 以收敛时长及算法复杂度为代价提高性能.
单形进化算法(surface-simplex swarm evolution, SSSE)是对BP神经网络输出与期望的误差函数进行优化, 其控制参数只有一个, 即种群数量, 避免了出现以增加控制参数提高准确率的问题.
2.2 SSSE优化BP神经网络
SSSE算法是基于单形邻域与多角色进化策略的智能优化算法. 该算法的实现原理为: 基于随机选取二维子空间, 利用定义的粒子单形邻域, 实现单形凸集逼近搜索[9], 提高粒子勘探局部区域与算法收敛的性能. 同时, 在搜索策略中引入粒子多角色态, 实现粒子多样化, 提高搜索的全局性[10]. 将BP误差函数作为SSSE算法优化的目标函数, 其实现优化的过程如图2所示.
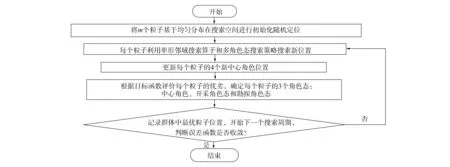
图2 SSSE-BP算法流程Fig.2 Flow chart of SSSE-BP algorithm
SSSE算法优化步骤如下:
1) 在搜索空间内对m个粒子进行初始化随机定位, 并采取均匀分布的原则:
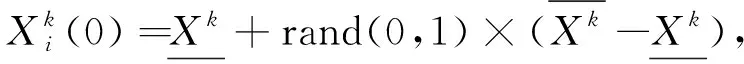
(2)

2) 在总搜索空间内, 将群体中所有的粒子按均匀分布的方式构建搜索子空间, 并随机选取两个维度a,b, 利用这两个维度, 使每个粒子在该搜索子空间内重新搜索新位置:


4) 根据所选取的目标函数, 对所得的每个粒子位置进行优劣性能判断, 利用其确定粒子的3个角色态: 中心角色态Xic(t+1), 表示每个粒子最终的最优位置; 开采角色态Xil(t+1), 表示粒子得到的最新位置; 勘探角色态Xig(t+1), 表示粒子以均匀分布的规则在搜索空间随机选取的位置.
5) 记录群体中最优粒子的位置Xoc(t+1), 循环步骤2)~5), 并对每次循环得到的最优解判断其收敛性, 直至误差函数收敛到给定的精度要求, 即认为算法完成寻优过程, 结束算法的寻优运算.
SSSE算法的优势是对粒子进行全局性的随机搜索寻优, 避免陷入局部最优值; 控制参数只有一个, 即种群数量, 而人工蜂群算法、 遗传算法、 粒子群算法等智能优化算法及其改进型算法, 都有较多的初始控制参数, 以增加控制参数提高准确率; 对于算法的可靠性, 在不同的随机初始化条件下, 50次内SSSE算法从未有偏离全局最优点的情形.
3 心音信号识别算法
3.1 数据来源
本文数据主要来源于丁香园论坛(http://www.dxy.cn/bbs/thread/30808564#30808564)提供的异常/正常心音信号. 本文选取9类异常/正常心音进行实验, 每类心音均含有多个信号, 9类心音信号分别为: 正常心音[12]、 第一心音减弱、 第二心音增强、 第二心音减弱、 二尖瓣关闭不全、 二尖瓣狭窄、 主动脉关闭不全、 二联律和心包摩擦音.
在进行心音信号分类时, 将所有心音样本分为训练集和测试集[13]两类. 训练集用于SSSE算法改进BP神经网络的训练心音样本, 共有90×9个训练样本. 测试集共有22×9个心音样本, 用于对训练好的网络进行测试, 并验证提出的基于SSSE算法优化的BP神经网络应用在心音识别上的性能.
3.2 算法流程
本文选择MATLAB作为试验平台, 研究目前已有心音信号分析模型的缺陷, 基于心音信号周期性的特点, 提出以FastPCA算法对心音信号进行特征提取降维, 以基于SSSE算法改进的BP神经网络作为模型核心, 最终实现对心音信号的识别分类[14].
模型实现步骤如下:
1) 首先对心音信号进行预处理. 利用小波变换对心音进行归一化、 去噪操作, 小波母函数为sym5, 分解层数为5.
2) 对心音信号进行特征提取降维. 心音信号未降维时, 样本维度为4 900. 本文采用FastPCA方法对信号进行降维, 先对样本去均值化, 然后求协方差函数, 对协方差函数求解特征值和特征向量, 按累计贡献率大小选取主成分的维度, 贡献率计算公式为
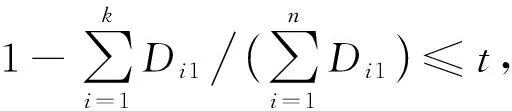
(11)
其中:D表示112×1维特征向量;n表示D的行数;k为最终选取的主成分的维度;t为可自设的误差. 多次实验结果表明, 当t=0.1, 累计贡献率为90%, 选取主成分的维度为36时, 心音识别率最高, 因此, 本文最终选取主成分维度为36.
3) 对降维后的心音信号进行归一化处理, 归一化方法为
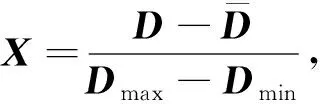
(12)
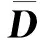
4) 初始化BP神经网络相关参数. 神经网络采用三层结构, 对比多次实验效果, 设置输入层神经元数为30, 隐含层神经元数为40, 输出层神经元数为3.
5) 将降维归一化后的训练集共810个心音样本输入经SSSE算法优化的BP神经网络中. 优化BP神经网络权值和偏置, 其中权值更新流程如下:
① 将m个粒子按均匀分布的规则在目标函数定义域内进行随机初始化定位;
② 对搜索空间内的每个粒子按单形邻域和多角色搜索策略搜索新位置;
③ 对每个粒子的4个中心角色位置进行更新;
④ 根据误差函数评价粒子的优劣, 以确定粒子的3个角色态: 中心态、 开采态和角色态;
⑤ 记录粒子的最优位置, 当粒子的收敛位置在所要求的精度范围内时, 停止搜索;
⑥ 将BP神经网络权值定为粒子的最优位置, 偏置与权值并行更新.
6) 将测试样本共198个心音周期输入训练好的网络中, 最终输出心音分类结果.
7) 对输出的心音分类结果进行统计分析, 得到心音识别率及误差曲线.
4 实验结果与分析
将上述9类心音各112个样本, 利用FastPCA算法进行降维特征提取, 得到9类112×36组数据, 选取部分特征值, 列举出9类心音各一组样本的特征值如图3所示. 每类选取90组用于SSSE-BP神经网络的训练, 22组用于测试, 各类心音识别率列于表1. 由表1可见, 9类心音共198个测试样本, 正确识别190个, 总体识别率为95.96%, 具有较好的识别率. 表2为本文经SSSE算法优化的BP神经网络与传统BP神经网络的心音识别率对比. 由表2可见, 本文模型的心音识别率为95.96%, 远优于传统BP神经网络模型的识别率. 上述两种实验方法结果的误差曲线如图4所示.
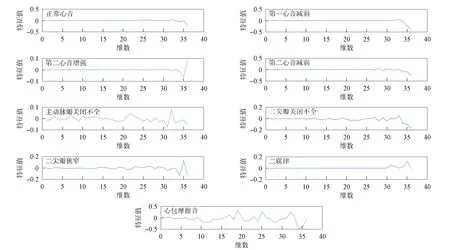
图3 9类心音的特征值Fig.3 Eigenvalues of 9 kinds of heart sounds

表1 各类心音识别率

表2 两种实验方法的心音识别率对比
由图4可见, 本文方法在迭代次数为1 000时, 误差函数值小于10, 基本处于平稳状态; 而传统BP神经网络模型在迭代次数为1 000时, 误差函数值大于60, 收敛效果明显不如SSSE-BP神经网络模型. 为了验证本文算法的收敛性, 以迭代次数t=3 000进行5次实验, 5次实验的平均误差曲线如图5所示. 由图5可见, 当迭代次数t=1 000时, 平均误差曲线趋于平稳, 当t∈[1 000,3 000]时误差由6降至3, 可认为达到了设置的收敛精度要求. 因此, 本文提出的基于SSSE算法改进的BP神经网络在学习过程中有效.

图4 两种实验方法误差曲线对比Fig.4 Comparison of error curves of two experimental methods
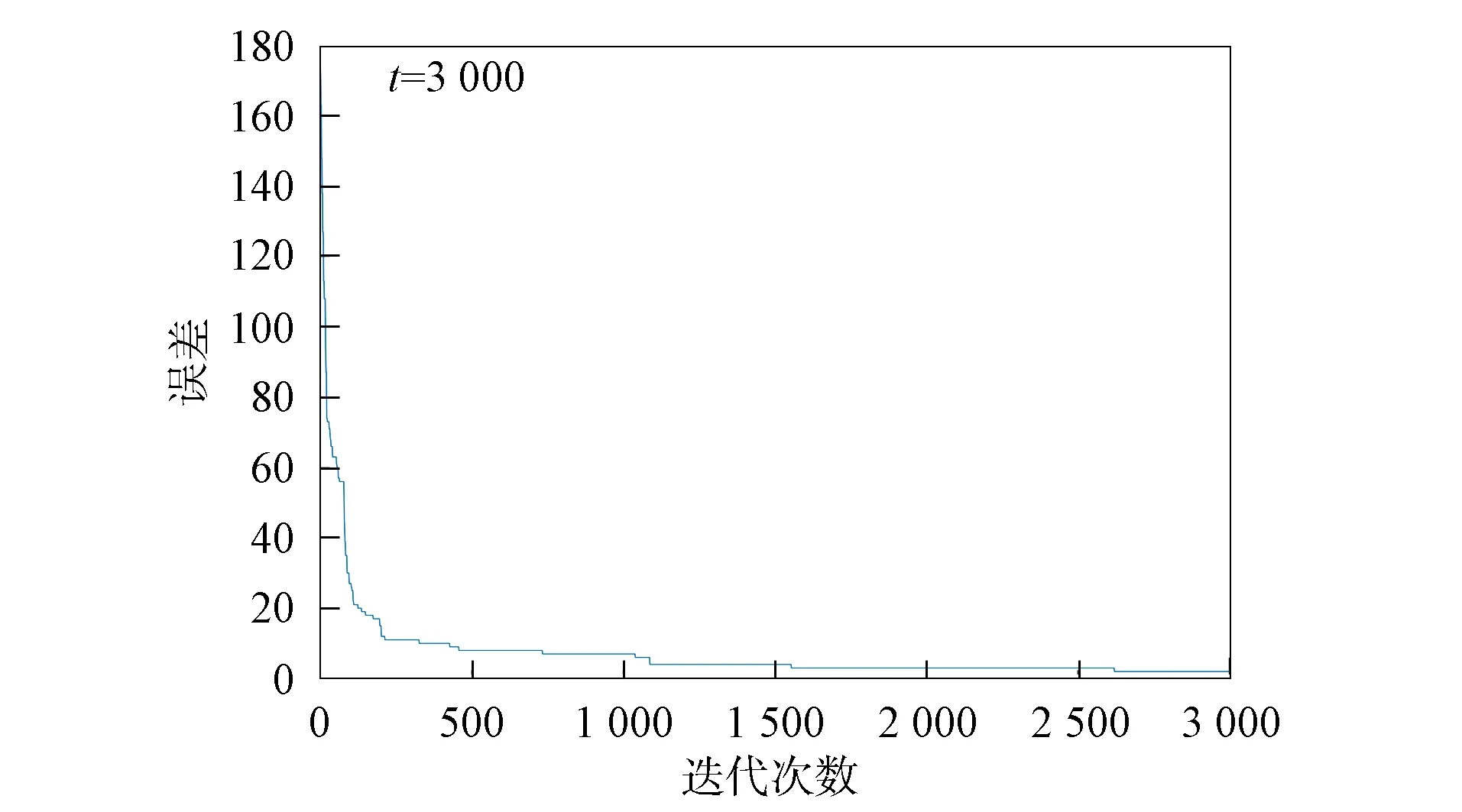
图5 5次实验的平均误差曲线Fig.5 Average error curve of 5 experiments
将本文方法与文献[15]中方法对心音分类的识别率进行对比, 结果列于表3, 其中文献[15]中采集的心音信号频率与本文中用于特征提取的心音信号频率均为11 050 Hz, 实验平台均使用MATLAB软件. 由表3可见, 本文算法能较好地应用于各种异常心音的识别分类, 且准确率分别比对比算法提高了4.9%,3.9%,1.9%. 实验结果表明, 本文给出的基于SSSE算法优化的BP神经网络模型准确率较高、 收敛性较好.

表3 采用不同算法时心音识别率的对比结果
综上所述, 针对改进BP神经网络的学习算法均以增加控制参数为代价提高收敛速度的问题, 本文提出了一种基于单形进化算法优化的BP神经网络学习算法, 即SSSE-BP神经网络. 实验结果表明, 在心音分类上本文算法明显优于其他对比算法的心音识别率.
