基于模糊信息粒化和优化支持向量机的氧化铝陶瓷超声磨削力趋势预测

赵明利 袁一鸣 李博涵 聂立新

（河南理工大学机械与动力工程学院，焦作 454000）

文 摘 为实现超声磨削氧化铝陶瓷中磨削力变化趋势的预测，提出了一种基于模糊信息粒化和支持向量机相结合的方法。首先进行氧化铝陶瓷超声磨削试验，然后利用模糊信息粒化方法对试验获得的磨削力进行粒化处理，并将人工免疫系统算法和粒子群算法进行并联混编构成人工免疫系统粒子群算法（AISPSO），接着建立非线性回归支持向量机预测模型并对模糊粒子进行预测，并通过AISPSO 算法优化支持向量机预测模型，最后获得超声磨削氧化铝陶瓷中磨削力的变化趋势和变化范围。结果表明：该方法可以有效实现超声磨削中磨削力的变化趋势及变化范围预测，且预测未来5 组数据变化范围的误差在10%以内，这为通过磨削力变化调整工艺参数以获得更好的加工表面提供了新的思路。

0 引言

陶瓷材料因其抗腐蚀、耐高温、耐磨损等优异性能，目前已广泛应用于汽车行业、机械行业以及航空航天等领域［1］。随着陶瓷材料的广泛应用，对其表面质量提出了更高的要求。由于超声磨削可以有效降低陶瓷加工中的磨削力［2］。同时磨削力也是表征磨削状态的重要加工参数，是影响被加工零件精度和表面质量的关键因素，所以通过对磨削力变化趋势进行预测，可以即时反馈调节加工参数，进而降低磨削力［3］，获得更好的表面质量。

目前切削力预测方面常用的预测方法包括有限元仿真［4-5］、BP神经网络［6-7］、支持向量机［8-9］等。如黄智［4］等基于磨削单位面积有效磨粒的砂带磨削力计算模型，通过有限元仿真模型实现对磨削力的预测；秦娜等［6］通过遗传算法优化BP神经网络建立磨削力预测模型，利用工艺参数对磨削力进行预测；张海鹰等［8］利用最小二乘支持向量机建立振动切削力软测量模型，并验证了该模型具有较高的建模精度和较强的泛化能力。但是这些预测方法大多采用经验公式建立仿真模型，或根据工艺参数来预测磨削力，然而实际磨削过程存在多种不确定因素，难以实现精确预测，而磨削力的变化趋势和范围的预测方法鲜有报道。本文提出一种基于模糊信息粒化（Fuzzy information granulation，FIG）和支持向量机（Support vector machines，SVM）在氧化铝陶瓷超声磨削中的磨削力变化趋势预测算法。

1 超声磨削的磨削力变化趋势预测原理

1.1 模糊信息粒化

模糊信息粒化就是用模糊集的方法对时间序列进行模糊粒化处理，最早由L.A.Zadeh 教授［10］提出，其中信息粒化就是将整体分解为一个个部分进行研究，每个部分为一个信息粒。采用W.Pedrycz的粒化方法［11］，其模糊粒子有高斯型、梯型、三角形和抛物型等。本文采用三角形模糊粒子，其隶属函数如下：

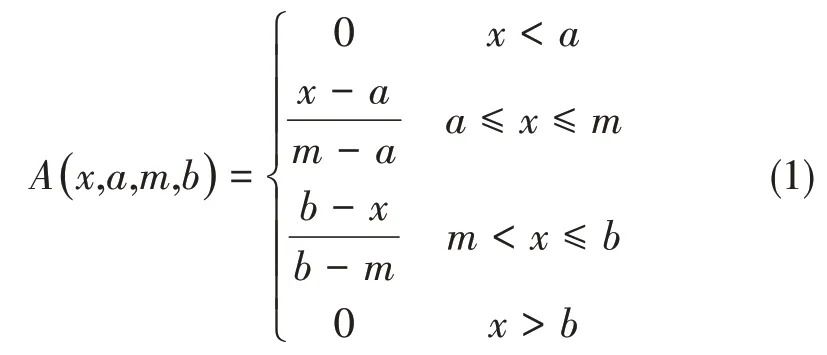
式中，x是论域中的变量，a、m、b为三角形模糊粒子的参数，a表示一个模糊窗口的最小值，m反映平均水平，b代表最大值。

1.2 非线性回归支持向量机预测模型

支持向量机［12］是一种基于统计学习理论的机器学习方法，具有完备的数学基础，且能够很好地应用于小样本、非线性、高维度等问题。其回归预测模型的基本原理就是利用非线性变换（核函数）将低维空间映射至高维空间，并在该高维空间中找到一种输入、输出间的线性关系［13］。

在支持向量机回归问题中，对于给定训练集样本D=｛（xi，yi）｝，i=1，2，3，…，l，其中xi∈Rn，yi∈R。可得到非线性回归函数：

式中，αi表示第i个x的系数，αi*表示最优解，b*表示偏置函数，K（xi，xj）表示核函数。

在支持向量机应用过程中，核函数及其参数选择至关重要。常用的核函数有多项式核函数、线性核函数、RBF 核函数和Sigmoid 核函数等。本文选取泛化性较强的RBF核函数，其公式如下：

式中，γ为核参数，且γ＞0。

在非线性回归支持向量机预测模型中，惩罚参数C和核参数γ对预测效果影响较大，且没有固定的参数选择方法。因此，本文通过智能优化算法对惩罚参数C和核参数γ进行选择。

1.3 人工免疫系统粒子群优化算法

人工免疫系统粒子群算法（Artificial immune system particle swarm optimization，AISPSO）由粒子群算法（Particle swarm optimization，PSO）和人工免疫系统（Artificial immune system，AIS）进行并联混编构成。通过亲和力评价算子、抗体浓度算子、激励度算子对粒子质量进行评价，并通过免疫选择算子、克隆增殖算子、变异算子对质量相对较差的粒子进行变异，保持种群粒子的速度，以保证粒子的多样性，改善了PSO算法易陷入局部收敛的情况，使之具有高效的寻优能力。

在AIS算法中，免疫选择策略是使高激励度粒子进入免疫操作、低激励度粒子消亡并初始化更新，其目的为保持并提高AIS 算法中的粒子质量。本文提出一种与之相反的选择策略，该策略使激励度相对较低的小部分粒子进入免疫操作，激励度相对较高的大部分粒子进入粒子群操作，并对阈值进行了改进，保证质量相对较好的粒子进入粒子群操作，质量相对较差的粒子进入免疫操作进行变异，保持种群的多样性，使种群陷入局部收敛后具有快速跳出的能力，其公式如下：

式中，Ta为阈值，abi表示粒子位置，act表示激励度。

为改善AIS 算法的变异策略有一定概率覆盖不到理论最优位置的问题，本文将最优位置转移至边界公式上［14］，并采用Tent混沌映射函数代替rand函数，采用的变异方案如下：

式（6）中，qL为当前搜索空间下限、qU为当前搜索空间上限，T为最大迭代次数，pg为当前全局最优。式（7）中，pm为变异阈值。

1.4 预测模型的评价标准

支持向量机回归预测模型的训练精度由均方误差MSE和平方相关系数r2评价，其公式如下所示：

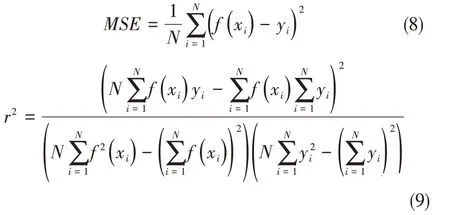
式中，N表示训练集个数，yi表示实测值，f（xi）表示预测值。MSE越接近于0，r2越接近于1 说明模型的训练精度越高。

磨削力变化趋势预测模型的预测精度由相对误差E衡量，由模糊粒子描述变化范围，若磨削力的实际变化范围为［a，m，b］，模型预测变化范围为［ya，ym，yb］，则误差E的公式为：

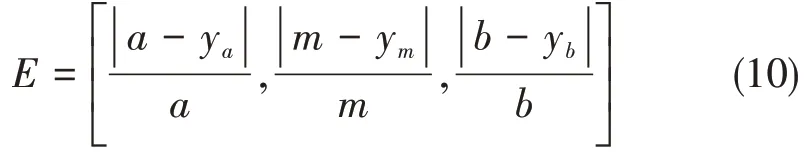
1.5 磨削力变化趋势预测流程

将模糊信息粒化方法与人工免疫系统粒子群算法优化支持向量机回归预测模型相结合，对超声磨削氧化铝陶瓷的磨削力变化趋势进行预测，其原理如图1所示。

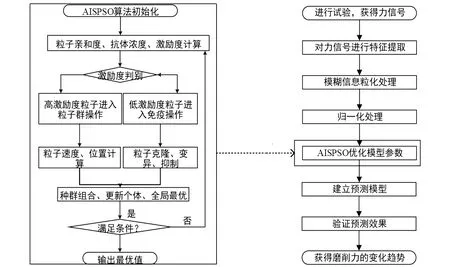
图1 磨削力变化趋势预测原理图Fig.1 Schematic diagram of prediction of grinding force change trend

2 超声磨削氧化铝陶瓷实验

2.1 装置与方案

为获得超声磨削氧化铝陶瓷中的磨削力变化趋势，采用VMC850E 立式加工中心和声学系统为主要设备搭建磨削试验平台，其中声学系统由超声波发生器、换能器、变幅杆及试件组成。试验时，磨削力信号通过Kistle9257b 测力仪传感器采集，测力仪的采样频率设置为30 kHz，超声振幅由KEYENCE 激光位移传感器测量仪测定，试件沿着变幅杆方向做纵向振动，砂轮对试件端面进行平面磨削，工艺参数及其他试验条件如表1所示。

2.2 结果分析

对测力仪采集的磨削力信号进行处理，从中提取出砂轮切入至砂轮完全切出这一时段的磨削力信号，信号中包含有时间、切向力、法向力以及径向力，本文选取时间和法向磨削力（下文简称磨削力）作为研究对象。

表1 超声磨削试验条件Tab.1 Conditions of ultrasonic grinding test

因磨削力信号的采集频率较高，导致采集的点数较多，不利于磨削力变化趋势分析，所以根据砂轮转速计算出砂轮旋转一周所需要的时间，以砂轮旋转一周的时间为采样周期，取每个周期的平均值作为磨削力的时间序列，则共有85 组数据。提取的磨削力时间序列如图2所示。

图2 磨削力的时间序列Fig.2 Series of grinding force time

从图2可知，磨削力呈现两段先增大后减小的变化趋势，且第二段增长趋势变缓。这是因为试验采用碗形砂轮，当砂轮运动到中间时会与试件分离，导致磨削力降到最低，接着砂轮再次磨削试件，但试件已经经过多次磨削，表面较为平整，再次磨削时磨削力会大幅减低。

3 超声磨削氧化铝陶瓷的磨削力变化趋势预测

3.1 磨削力的模糊信息粒化

将85组磨削力数据进行划分，前80组作为训练集，后5组作为测试集，并根据三角形模糊粒子对训练集进行信息粒化处理，粒化窗口大小设置为5，共有16个窗口。磨削力的模糊信息粒化结果如图3所示。第16个窗口由模糊粒子描述的磨削力变化范围为［6.175 1 6.366 7 6.502 3］。由图3可以看出，三角形模糊粒子很好地模拟了磨削力的变化趋势。。

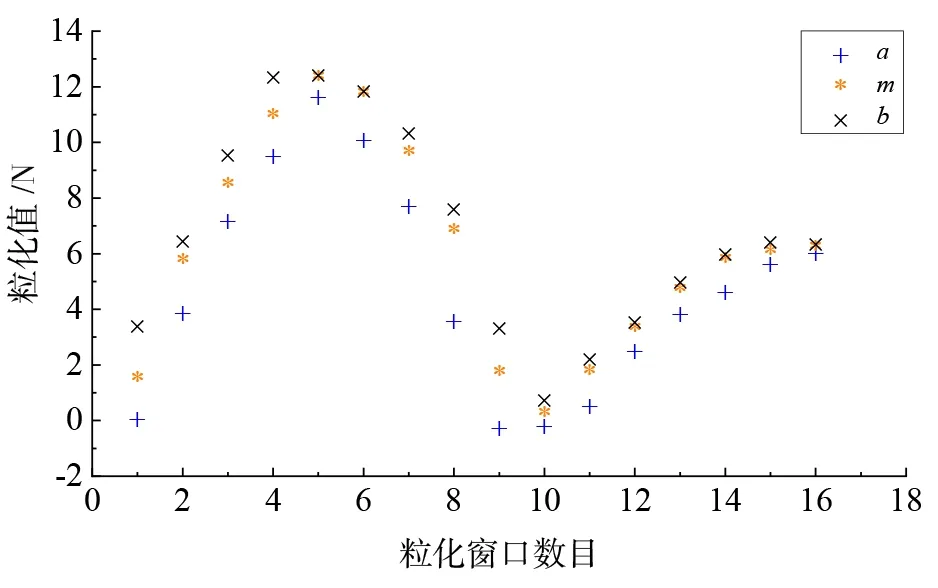
图3 磨削力的粒化结果图Fig.3 Graph of grinding force granulation results

3.2 SVM回归预测模型的参数优化及其评价

将AISPSO 算法进行初始化，并对SVM 的惩罚参数C和核参数γ进行迭代寻优，其适应度设置为k折交叉验证误差最小，其中k折交叉验证指将数据分为k组，每次将k-1 组作为训练集，剩余一组作为测试集，循环k次，将这k组模型的预测精度的平均值作为训练精度，本文k取5。

为使AISPSO 算法的寻优精度更高，将算法的进化代数设置为500，种群最大数量设置为50，SVM 的惩罚参数C和核参数γ的寻优范围设置为［2-7，210］，其他参数设置如表2 所示。三个模糊粒子参数的SVM回归预测模型参数优化结果如表3所示。

将上述通过AISPSO 算法优化的最优惩罚参数C和核参数γ用于SVM 模型训练，得到的训练结果如图4所示，使用均方误差MSE和平方相关系数r2对模型进行评价，其结果如表4所示。从表4可知，a，m，b三个参数的SVM 回归预测模型精度较高，模型均方误差MSE最小可达0.013 513，平方相关系数r2最大可达0.999 857；从图4中可以看出，预测模型能够实现对训练样本的精确模拟。

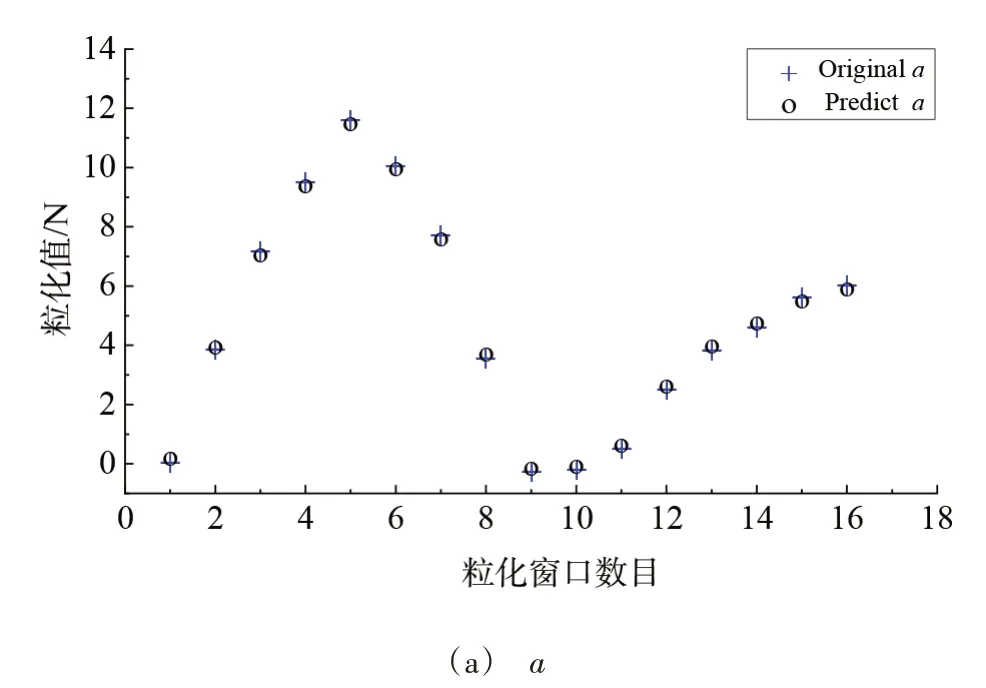
表2 AISPSO算法参数设置Tab.2 AISPSO algorithm parameter settings

表3 SVM模型参数优化结果Tab.3 Results of SVM model optimization

图4 SVM模型训练结果Fig.4 Results of SVM model training

表4 模型均方误差和平方相关系数Tab.4 Model mean square error and square correlation coefficient

3.3 基于SVM回归模型的磨削力变化趋势预测

使用测试集对优化后的SVM 预测模型进行验证，将训练优化后的SVM 回归预测模型用于预测未来一个模糊窗口（窗口大小为5），其结果如表5 所示，其中实测范围值由编号为81～85的实测磨削力模糊信息粒化获得；预测范围值由表3 得到的SVM 模型预测获得；预测相对误差E由公式（10）获得。

从表5 中可以看出，预测的未来5 组磨削力变化范围误差在10%以内，与前5组（图3第16窗口）磨削力数据相比，磨削力有变小的趋势。加工时可根据磨削力变化趋势即时对工艺参数进行调整，以获得更好的表面质量。

3.4 改变周期大小

探究在磨削力信号特征提取时周期大小对模型精度的影响。分别选取砂轮旋转1周、2周、3周、4周的时间作为采样周期，粒化窗口大小设置为3，其他条件不变，不同周期大小预测模型的相对误差如表6所示，其中预测相对误差E由公式（10）获得。

从表6 中可以发现，当周期逐渐变大时，预测相对误差变大，预测精度逐渐降低，3 周之后精度则无法保证，这是由于周期变大提取特征中有效信息严重丢失，使算法预测效果变差。

4 结论

（1）基于模糊信息粒化方法和人工免疫系统粒子群算法优化支持向量机回归预测模型，实现了对超声磨削氧化铝陶瓷的磨削力变化趋势及变化范围预测，且预测的磨削力变化趋势相对误差在10%以内。

（2）采用改进的人工免疫系统粒子群算法优化支持向量机回归预测模型，提高了预测模型的训练精度，其模型均方误差MSE最小可达0.013 513，平方相关系数r2最大可达0.999 857。

（3）对磨削力信号特征提取时的周期大小选择进行了讨论，得到以砂轮旋转1周的时间作为采样周期时，能获得较高精度。

表5 磨削力的变化趋势及变化范围Tab.5 Change trend and range of grinding force

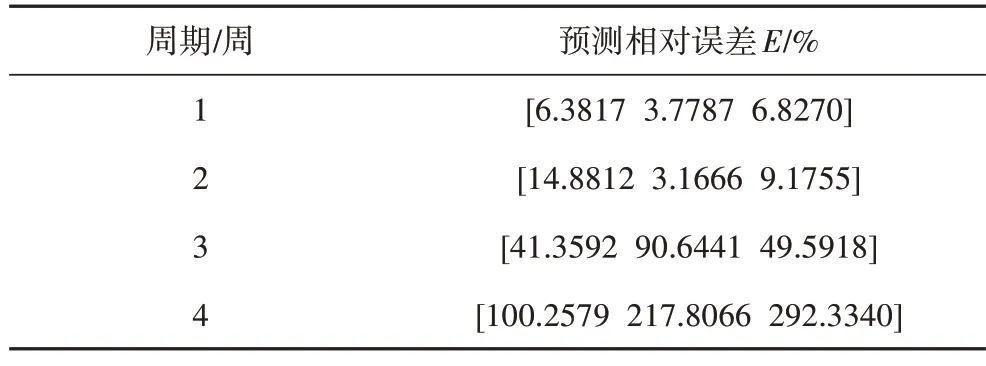
表6 磨削力不同周期的预测相对误差Tab.6 Relative error of grinding force prediction in different periods