基于改进型近场动力学方法的复合材料单向板变形与破坏分析

秦洪远 李 玲 王 伟 许波凯 郑 印

（上海复合材料科技有限公司，上海 201112）

0 引言

纤维增强复合材料一般由基体材料与增强纤维组成，因其具备高比强度、比模量、耐腐蚀以及可设计性强等优点而被广泛应用于航空、航天、汽车、兵器等工程领域。然而，在充分发挥基体材料与增强纤维优异性能的同时，纤维增强复合材料在服役过程中也不可避免地存在基体开裂、纤维断裂、纤维拔出等破坏问题，且由于纤维增强复合材料多为宏观各向异性，探究其破坏机理较传统各向同性材料更为困难。考虑到单层板作为层合板等复合材料成型的基本单元，广大科研工作者早期对单向铺层板的失效破坏问题开展了试验研究与理论分析［1-2］。由于试验研究与理论分析分别面临着成本高昂与求解困难等问题，难以满足日益增长的工程需求，近几十年来，数值方法蓬勃兴起并被用于研究复合材料单向板破坏问题［3］。

诸如有限元等传统基于连续介质理论的数值方法，分析材料和结构弹性变形时具有较高的定量计算精度，但是对于分析损伤、破坏等不连续问题时，需要进行网格重构等特殊处理手段，导致计算过程繁琐，计算精度较低。究其本质是由于偏微分形式本构方程在处理不连续问题时存在奇异性。为了从根本上解决这一问题，采用积分形式本构方程的近场动力学应运而生［4-5］，并且已经被证明能够有效处理材料和结构的变形与破坏问题［6-7］，在近场动力学方法中裂纹可以自发扩展，不需要引入额外的网格处理手段。

针对于复合材料单向板的研究，OTERKUS等［8-9］基于近场动力学理论提出了用于分析复合材料单向板的理论模型，并用于单向板拉伸破坏问题分析。然而目前已有的单向板分析模型未能考虑非局部长程力的尺寸效应，因此定量计算精度相对较低。HUANG 等［10-11］曾引入核函数修正项对各向同性材料的变形进行定量计算，验证了修正后的模型具备更高的定量计算精度。

本文在传统单向板分析模型基础上，引入能够反映长程力尺寸效应的核函数修正项改进近场动力学本构模型，构建相应的近场动力学准静态求解体系，通过对单向板的变形进行定量计算，验证所提出的改进型近场动力学模型具备更高的定量计算精度。进一步开展含不同角度中心裂纹单向板的拉伸破坏试验与数值模拟，对比二者所得结构最终破坏形式与破坏特点，验证所提出的近场动力学模型与方法能够有效处理单向板的破坏问题。最后对纤维角度为0°单向板的拉伸破坏过程进行模拟分析。

1 PD基本理论与模型修正

1.1 PD基本理论

如图1 所示，在任一时刻t，空间域R内部任意物质点x与其近场范围H（半径为δ的球域）内另外任一物质点x′间存在单位体积相互作用力f（点对力）：

式中，u、u′、x、x′分别表示物质点x和物质点x′的位移和位置，η、ξ表示两物质点的相对位移和相对位置［5］。该物质点处的运动方程可以表示为：

式中，ρ为材料密度，b为外力密度，dV′为该物质点包含的体积。

在键型PD 理论体系中，若将空间域内物质点间的相互作用（键）看作中心弹簧的铰接杆单元［12］，仅考虑物质点间的法向作用，此时点对力可以表示为：

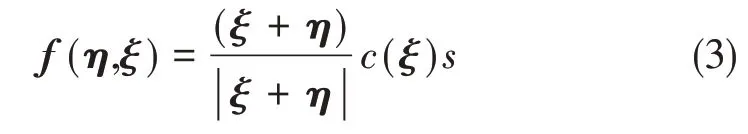
式中，c(ξ)为物质点对（键）的拉伸微模量系数，表征物质点对的拉压刚度，若不考虑物质点间非局部长程力的尺寸效应，此时c(ξ) =c。s为物质点对的伸长率，其表达形式为：

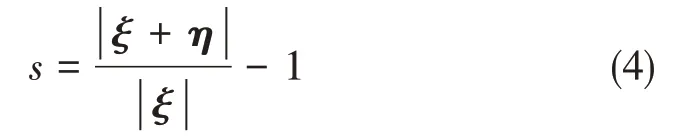
为了描述复合材料单向板的宏观各向异性，将物质点间（键）的作用区分为基体键与纤维键，若纤维方向为θ，物质点对的拉伸微模量系数可以表示为：

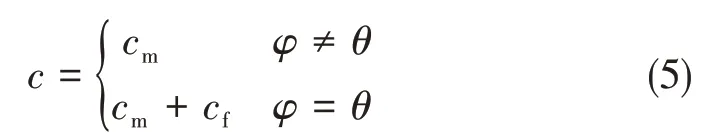
式中，cm、cf分别为基体键与纤维键的拉伸微模量系数，纤维键仅在纤维增强方向存在［8］。基于小变形假定，|ξ+η|≈|ξ|+|η|，若令|ξ|=ξ、|η|=η，根据式（4）可得η=sξ。由于当前模型将物质点间的相互作用（键）看作中心弹簧的铰接杆单元，可类似于弹簧弹性变形能计算确定物质点对（键）的弹性变形能：

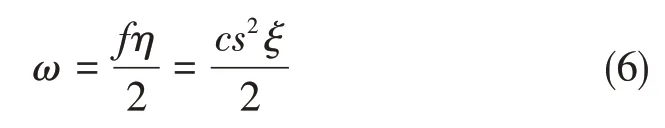
ω也被称为点对势能密度。通过对任一物质点x与其近场范围内所有物质点间“键”的弹性变形能求和，即可确定物质点x所占空间域的弹性变形能：

图1 物质点间相互作用Fig.1 Interaction of material points

式中，Q表示物质点x近场范围内纤维键数，1/2 表示“键”所具有的变形能均分给该“键”上物质点。Vq为物质点x近场范围内另一物质点所占空间体积，其表达式为：

式中，N为近场范围内物质点总数，th为单向板厚度。进一步将式（7）中PD 表达的弹性变形能与经典弹性理论应变能等效。即可得到物质点对拉伸微模量系数的表达式：

此模型即为OTERKUS 等［8-9］所提出的单向板分析模型。当纤维角度确定，该模型的微模量系数均为固定值，因此未能反映非局部长程力的尺寸效应。

1.2 PD模型修正

在已有模型［8］基础上引入HUANG 等［10］所提出的核函数修正项g(ξ) =[1-(ξ/δ)2]2，将式（5）中的基体键拉伸微模量系数修正为：

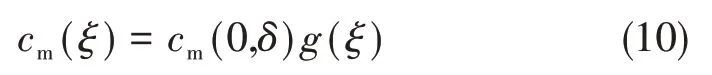
进一步将物质点对（键）的弹性变形能与应变能等效，确定修正后的表达式：

此时基体键拉伸微模量系数不再为固定值，能够反映非局部长程力的尺寸效应。对于各向同性材料，E1=E2，模型可退化为HUANG 等［10］所提出的近场动力学本构模型。

1.3 PD损伤定义

在键型PD 理论体系中，以物质点对（键）为计算的基本单位，可在“键”的层次上基于统计思想定义局部损伤［12］，即：

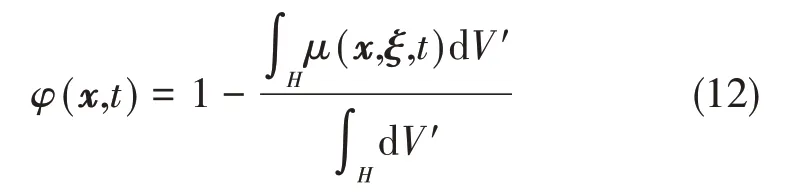
式中，φ(x，t)表示局部损伤值，φ(x，t) = 0 表示无损，0 ＜φ(x，t) ＜1表示不同程度的损伤，φ(x，t) = 1表示完全损伤状态，μ(x，ξ，t)为表征物质点间“键”断裂与否的间断函数：

式中，sf和sm分别表示纤维键与基体键的伸长率，sft0、sfc0、smt0、smc0分别表示纤维键与基体键的拉伸、压缩临界伸长率。

1.4 PD基本求解体系

为了获得准静态解，在式（2）中引入人工阻尼加速收敛，若令，经均匀离散可得：

式中，C为人工阻尼。刘一鸣等［6］曾分析阻尼对于求解收敛性的影响，提出了适当的阻尼选取区间，在本文研究中C= 2 × 106kg/(m3· s)。采用中心差分格式对时间序列进行均匀离散可得：

式中，Δt表示时间步长增量，将式（15）带入式（14）中可求得迭代计算公式：

通过反复迭代求解即可获得任意时刻结构内任一物质点的位移信息，了解其受力状态，最终确定整个结构的弹性变形、局部损伤到整体破坏的各个过程。

2 算例分析

2.1 单向板变形定量计算

对图2所示单轴拉伸单向板变形进行定量计算，单向板尺寸为L=160 mm，W=60 mm，材料参数具体为：弹性模量E1= 325 GPa，E2= 9 GPa，泊松比ν12=1/3，纤维方向θ=0°，均布拉伸荷载P=3.25 GPa，离散间距Δx= 0.5 mm，近场范围半径δ= 3Δx［12］，经均匀离散获得38 841个物质点。

图3所示分别为PD模拟与理论求解所得单向板x、y轴线处物质点位移ux、uy随x、y方向位置的变化曲线，使用已有PD 模型与改进型PD 模型所得定量计算结果较理论解的相对误差分别为3.5% 和1.7%，相较于已有模型，改进型PD 模型具备更高的定量计算精度。

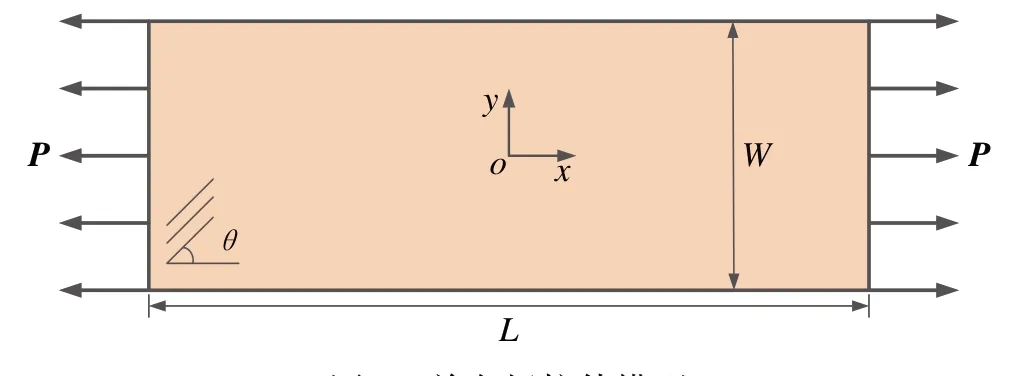
图2 单向板拉伸模型Fig.2 Unidirectional plate model under tension

图3 单向板x、y轴位移图Fig.3 Displacement diagram of unidirectional lamina along x and y

2.2 中心裂纹单向板拉伸破坏试验与数值模拟

如图4 所示，采用M55J/AG80 预浸料（纤维体积分数60%±3%，单层厚度0.1 mm）单向铺层制备单向板，纤维方向θ=45°，单向板厚度th= 0.5 mm，试验件外形尺寸与2.1节一致，采用电子万能材料试验机进行拉伸破坏试验，为了避免在试验过程中夹持区域率先发生脆性破坏，使用J-133胶黏剂在夹持区域胶接宽度b=40 mm 的玻璃钢垫片，预置中心裂纹长度30 mm，宽度1 mm，中心裂纹与纤维方向夹角β分别为0°、45°、90°。采用PD模型与方法建立相同工况下的数值模型，材料参数与2.1 节一致，纤维键与基体键的拉伸、压缩临界伸长率分别为：sft0= 0.01、sfc0=0.01、smt0= 0.005、smc0= 0.01。

图4 单向板拉伸试样Fig.4 Unidirectional plate sample under tension

图5 所示分别为PD 模拟与试验所得β=0°、45°、90°时单向板的最终破坏形式，裂纹均由预置裂纹尖端沿纤维方向扩展至结构边缘，其破坏形式均为基体开裂。β=0°、45°时，PD 模拟结果与试验结果高度吻合，当β=90°时，试验件玻璃钢垫片边缘存在10 mm×10 mm 区域沿纤维方向的基体开裂，PD 模拟结果中未能反映这一现象，但二者所得裂纹扩展路径基本吻合。这表明所提出的近场动力学方法能够有效模拟复合材料单向板的破坏过程。

2.3 中心裂纹单向板拉伸破坏分析

对纤维角度θ=0°单向板的拉伸破坏过程进行数值模拟，模型尺寸、材料参数与2.2节一致，预置中心裂纹与纤维夹角α分别为0°、45°、90°。由于本节主要研究θ=0°单向板的拉伸破坏特性，而夹持区域为无损区域，因此后续数值模拟结果不显示夹持区域。

如图6所示，对于含不同角度中心裂纹θ=0°单向板的破坏过程基本一致，裂纹均由预置裂纹尖端起裂，沿纤维方向扩展，直至夹持区域边缘，此时结构主要为基体破坏，随着进一步加载，整个结构内出现大范围的基体损伤，靠近夹持区域出现纤维断裂，最终出现贯穿整个结构的断面导致单向板发生破坏。对比2.2 节中θ=45°时单向板的破坏特点，θ=0°单向板在破坏过程中除基体开裂外，还会出现纤维断裂。

图5 单向板破坏形式Fig.5 Failure model of unidirectional plates

图6 单向板裂纹扩展过程Fig.6 Crack propagation process of unidirectional plates

3 结论

（1）提出了一种改进型PD 本构模型，推导了相应的微模量系数，构建了PD 准静态求解的数值体系，通过对典型单向板的单轴拉伸变形进行定量计算，所得数值结果与理论解比较，验证了改进型PD本构模型具备更高的定量计算精度。

（2）开展了含不同角度中心裂纹θ=45°单向板的单轴拉伸破坏试验与数值模拟，所得最终破坏形式吻合较好，且二者均能反映单向板基体开裂的破坏特点，表明所提出的PD 模型与方法能够有效处理复合材料单向板的破坏问题。

（3）对含中心裂纹θ=0°单向板的拉伸破坏过程进行数值模拟，结果表明，θ=0°单向板在前期裂纹扩展过程中主要出现基体开裂，当裂纹扩展至夹持区域后，结构出现纤维断裂，最终形成贯穿整个结构的断面导致单向板破坏。