例谈直觉思维在解题中的运用

刘喜兰

[摘  要] 直觉思维是人类重要且常见的思维形式，在人的创造思维能力中占有举足轻重的地位. 文章结合多个例题，从直觉观察、直觉猜想和渗透思想等方面透析直觉思维的融入，具体呈现了解题中处处存在直觉思维，解题教学中处处可以渗透直觉思维的特点，希望能以微观映射宏观，为广大数学教师的教学提供指导和实践的方法，从而提高学生的思维品质和学科素养.

[关键词] 解题;直觉思维;观察;猜想;数形结合

在课堂观察和调查中，笔者发现：在解题中，教师往往更注重训练学生的逻辑思维，关注学生逻辑严密性的培养，而直觉和预见的过程匆匆而过，这种教学功利性较强，忽视了直觉思维在解题中的顿悟作用和导向意义，导致学生学习动力不足，联想和想象能力缺失，从而在一定程度上限制了学生思维能力的发展，这与新课程理念背道而驰.

所谓直觉，就是从联想空间出发，将零碎的、单一的信息进行关联和组合，整合为新的有价值的信息. 数学直觉就是指摆脱固定逻辑规则的束缚，对数学对象的一种直接领悟或洞察. 所以直觉思维在解题中有不可低估的作用，教师在授课的同时应注重对直觉思维的训练.

深入观察，直达目标

观察是一种直觉活动，它是处理复杂问题时的一种感知活动，敏锐的观察力可以帮助学生一眼看穿问题的本质，快速形成解题路径. 因此，在解题教学中教师可以引导学生关注数学问题的结构特征、数形特征、数式特征、图形特征等，充分运用直觉思维，敏锐做出判断，形成解决问题的策略.

1. 对数式特征的观察

例1：已知一个四边形的四条边长依次为25，39，52，60，且该四边形内接于圆O，则圆O的周长为（  ）

A. 65π B. 64π

C. 63π D. 62π

分析：试题以四边形为载体，题型为一道选择题，表述较为简洁，体现了数学抽象，重点考查学生的数感，主要考查学生的直觉思维能力. 不少学生在解题时不注意观察，读出题意发现需求外接圆半径，便经验主义地从解三角形的方向进行探究，从而导致思维卡壳.事实上，学生需要认真读题和深入观察，借助答案所呈现的信息进行思考，只有深入观察并借助直觉思维准确定位39，52，65及25，60，65分别为一组勾股数，才能得出外接圆周长为65π，故本题选A.

2. 对结构特征的观察

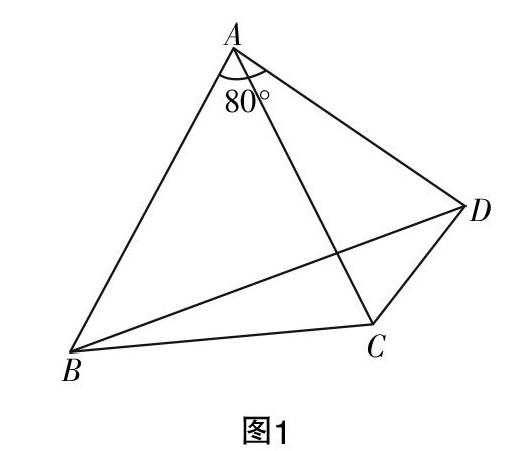
例2：如图1，在凸四边形ABCD中，有AB=AC=AD，∠BAD=80°，试求出∠BCD的度数.

分析：在本题的探究中，一些学生难以制定准确的解题策略，感到一筹莫展.实际上，此时可以不忙着答题，而是引导学生去观察条件中式子的结构，从AB=AC=AD着手，可以将A视为圆心，则有AB、AC和AD为圆A的半径，不难得出∠DAB为圆心角，从这个现象中很快看出“门道”，∠BCD为280°弧所含的圆周角，则有∠BCD=■=140°.

3. 对结论特征的观察

例3：已知P1P2=2（q1+q2），证明：方程x2+P1x+q1=0和x2+P2x+q2=0中至少有一个方程有实根.

分析：本题中命题结论呈现多种特征，要分类讨论的情形太多，直接处理不太好入手，而反面只有一种情形，也就是“两个方程都没有实根”，从而可以通过反证法来完善解题路径.

证明：设两个方程都无实根，则有Δ1=P■-4q1<0，Δ2=P■-4q■<0，则Δ1+Δ2=P■+P■-4（q1+q2）<0. 据条件P1P2=2（q1+q2），可得Δ1+Δ2=P■+P■-2P1P2=（P1-P2）2<0，显然与（P1-P2）2≥0相矛盾，则方程x2+P1x+q1=0和x2+P2x+q2=0中至少有一个方程有实根.

反证法的思想独特，需要借助于直觉思维的参与，快速洞悉并形成思维路径，同时，还可以训练学生逆向思维能力，有效提升思维品质.

直觉猜想，出其不意

只有全面认识猜想与直觉之间的关联才能准确定位直觉思维在解题中的作用，从而更好地应用. 不少学生在解题中会猜想是不是这样的方法，或者是不是这个出发点，然后通过探索实践，证实自己的猜测，从而形成解题思路和方法.通常这样的解题过程，不仅可以更好地训练直觉思维，而且能提高解题能力，促进思维发展.

1. 实验猜想

例4：计算■×■+1 ■的值.

分析：首先，取n=1，2，3进行实验，并记所求值为Sn.

当n=1时，S1=9×9+19=102;

当n=2时，S2=99×99+199=（100-1）·（100-1）+（200-1）=1002=102×2;

当n=3时，

S3=999×999+1999=（1000-1）·（1000-1）+（2000-1）=10002=102×3

……

从而猜想易得Sn=（10n-1）（10n-1）+2×10n-1=102n，可得Sn=102n.

从以上例题可以看出，猜想在具体解题中有着十分重要的作用，可以使不少数学题目，尤其是难于上手的数学题，通过猜想轻而易举獲得解题思路. 而这种猜想是在直觉思维的作用中逐步培养起来的.

2. 条件猜想

例5：设x，y，z∈R，且各不相等，有x+■=y+■=z+■，求证：x2y2z2=1.

分析：若不能把握住条件“x，y，z∈R，且各不相等”进行猜想，则很难找到解决本题的突破口. 事实上，通过直觉思维进行猜想，容易想到解题过程中定会出现因式（x-y），（y-z），（z-x），从而根据以上因式联想解题路径，容易生成以下解题方法：

因为x+■=y+■，所以x-y=■-■=■，则yz=■.

同理可得zx=■，xy=■.以上三式相乘，即可证得x2y2z2=1.

渗透思想，直达目标

数形结合是数学思想中最能训练学生直觉思维的，它借助“数”的精确来阐明“形”的属性，或提供“形”的形象来表述“数”的关系，实现“数”与“形”的转化，可以化抽象为直观，从而形成跳跃式的直觉思维，实现优化解题的目的.

例6：已知n为正实数，且a，b，c，d均为比n小的正数，求证：■+■+■+■<4n.

分析：本题若采用代数法进行求证，学生极易思维卡壳，无法探究到解题思路.观察本题条件，并联想到（n-a）+a=（n-b）+b=（n-c）+c=（n-d）+d=n;与此同时，还能再联系到“直角三角形的斜边是左边每个根式”的几何意义. 在这样的启发下，解决本题则有了以下思考：如图2所示，四边形A1B1C1D1的周长与不等式左边的几何意义相同，有A1D=a，A1C=n-a，AB1=b，B1D=n-b，BC1=c，AC1=n-c，D1C=d，BD1=n-d. 由于四边形A1B1C1D1的周长小于正方形ABCD的周长4n，所以■+■+■+■<4n.

图析的过程直观明了，借助几何的“形”，使数学的计算脱离了形式法则与抽象定律，让计算的每一步结果都有了显性化的载体，赋予了每一个解题步骤合理的阐释，解决问题的思路在几何直观下自然显现. 所以说，数形结合是一座沟通代数和几何的桥梁，可以提高学生对数学内部建设的直观认识，丰富解决问题的策略.

总之，在面向全体学生的数学解题教学中，引导学生运用直觉思维进行思考，是一种值得提倡的策略，不仅可以提高学生的解题能力，形成数学活动的基本经验，还能满足学生终身发展的需求.在解题教学中，运用直觉思维，首先要精心设计具有引领性和启发性的典型例题，促进学生进入深层次的思维状态，从而自然探寻直觉解题思维策略;其次，还需引导学生深入观察、直觉猜想、渗透思想，以达到举一反三的目的;再次，还需引导学生形成解后反思的良好思维习惯，以达到触类旁通之功效.