浅谈中学数学课堂教学培养学生创新能力的策略

凌海霞

[摘  要] 当前，以数学课堂培养学生的创新能力的教学理念已被广大教师所认同，在教学中如何落实创新能力的培养是我们一直努力的方向. 文章中笔者结合自身的教学实践，就如何在高中数学课堂教学中培养学生的创新能力进行了一些尝试，即技巧导课，展开创新教育;质疑问难，促发创新意识;参与学习，激发创新能力;思维求异，生成创新能力.

[关键词] 课堂教学;创新能力;导课;质疑问难;思维求异

创新精神是新世纪人才的必备特质，从而新世纪创新人才的培养是当下基础教育改革中的一项迫切任务. 创新是一个民族进步的灵魂，是一个国家兴旺发达不竭的动力. 而教育在培养创新精神和创新人才方面有着不可推卸的特殊责任和使命. 因此，学校担负着培养学生创新能力的重任. 而学生的思维活动大多是借助课堂教学来实现的，那么这就意味着课堂是学生创新能力发展的主要渠道. 作为数学教师，应以教材作为媒介，将创新能力与教学过程相沟通，在落实“双基”的同时培养学生的创造性思维能力[1]. 本文就常规教学中培养学生的创新精神和创造思维，将笔者自己的一些粗浅做法与大家共同交流与探讨.

技巧导课，展开创新教育

以“创新能力”为课程目标的改革在数学课堂教学中如火如荼地展开，创新思维不仅有助于学生良好学习习惯的养成，还可以帮助学生摆脱思维定式的束缚，对综合思维能力的提升具有导向作用. 因此，教师需从学生的具体学情出发，投其所好，将培养学生的创新思维根植于情境之中，从而有技巧地实施导课，以质疑、激趣、悬念等方式引入课堂，展开创新教育. 而任何一种技巧导课的本质都是基于学生的已有认知结构的基础上创设“矛盾式”问题情境，激发学生的认知冲突，引发一系列矛盾. 此时，教师将这些矛盾与冲突代入对应的数学课堂中，引领学生在激烈的讨论中解决矛盾，在自主探究中领略数学风采和解决数学问题.

例如，笔者在执教“反正弦函数”中，借助以下问题导入课堂：以下三个函数y=2x，y=x2，y=sinx，是否存在反函数？若存在，请指出;若不存在，请阐明原因. 在判断y=2x时，学生可以毫不犹豫地做出判断，并给出答案;当判断y=x2时，学生给出了不存在的结论. 笔者拾级而上，问：“当x在什么范围内，y=x2存在反函数呢？”学生经过一段时间的思考和讨论解决了这一问题，进而问题推进到y=sinx上. 学生同样经过探究后总结出：当y=sinx在2kπ-■，2kπ+■（k∈Z）上具有单调性，即存在反函数. 教师适时提问：“那么该选取哪个区间呢？”学生再一次展开了激烈的讨论，得出-■，■这个区间的答案，并出示理由：此区间在运算上具有简洁性，且又具有对称性.

质疑问难，促发创新意识

学生质疑问难能力的提升是培养创新人才的关键所在. 因此，在数学课堂教学中，教师需摒弃“以考施教”的观念，做学生创造性思维的引发者，让学生将被动学习转换为主动学习，充分诱导学生质疑问难，使学生获得进步. 实践证明，质疑问难下的课堂教学，学生学习积极主动，学习过程生动有趣，易在争辩中自然生成知识技能.

例1：设f（x）=■，且y=g（x）的图像与y=f-1（x+1）的图像关于y=x对称. 试求出g（3）的值.

教师引导学生做出以下解答：因为y=g（x）和y=f-1（x+1）互为反函数，则本题可以先求y=f-1（x+1）的反函数. 因为x+1=f（y），即x=f（y）-1，将x与y交换可得y=f（x）-1，所以g（3）=f（3）-1=■-1=■.

生1提出不同的解法：首先求得f（x+1）=■=■，所以g（x）=f（x+1）=■，所以g（3）=■.

生1这种解法的关键点是f（x+1）和f-1（x+1）互为反函数，我们可以设f（x）=x，那么f（x+1）=x+1，f-1（x）=x，f-1（x+1）=x+1，显然它们并不互为反函数，因此此解法是错误的.

例2：若a>0，b>0，且有a+b=1，证明：a+■b+■≥■.

部分学生给出如下错误的解法：因为a>0，b>0，所以a+■≥2，b+■≥2，所以a+■b+■≥4.

很快，有一些学生发现了该解题过程出错了. 通过思考不难看出，不等式a+■≥2当且仅当a=1时等式成立，同理，不等式b+■≥2当且仅当b=1时等式成立，因此即当a=b=1时，a+■b+■≥4的等式才成立. 而这里很明显与题设a+b=1不符合，所以此解法是错误的. 从以上错误解题思路中，有学生生成猜想，若有a=b，那么应当a=b=■. a+■b+■=ab+■+■+■≥ab+■+■+2≥2×■+■+2=■. 当且仅当a=b=■时，上述等号成立.

本题中正是有了错误的证法，才能形成后面的猜想和证明过程. 这也就说明，学生的数学思考与质疑问难的发展过程是同步进行的，两者是相互促进、协调发展的. 执教者让学生展示解题思路和提出问题的过程，其实就是给予学生质疑问难的机会，就是将这个解题活动定位于“思维—猜想—质疑—验证”型解题过程，这个过程具有明显的创造性思维特征，一定程度上是对学生思维独创性、变通性的观照.

参与学习，激发创新能力

在课堂教学中，教师需有效沟通学生与教材，从创新思维的视觉，充分认识到教学内容的核心价值，进而准确有效地把握教学重心，通过层层递进、指向明确的教学过程来激发学生的思维火花，并不断调整和优化教学过程，从而激发学生的创新能力[2].

例3：設奇函数f（x）的定义域是R，且该函数也为减函数，当0<θ<■时，f（cos2θ+2msinθ）+f（-2m-2）>0，试求出m的范围.

生1：据函数性质可得cos2θ+2msinθ<2m+2成立，即sin2θ-2msinθ+2m+1>0（0<θ<■）成立. 令t=sinθ，则可以将问题转化为t2-2mt+2m+1>0在区间（0，1）上成立，而后借助分类讨论可得m≥-■.

师：还有不同答案吗？

生2：m<1-■.

师：你这个答案是如何得出来的呢？能和大家简单说一说你的解题思路吗？

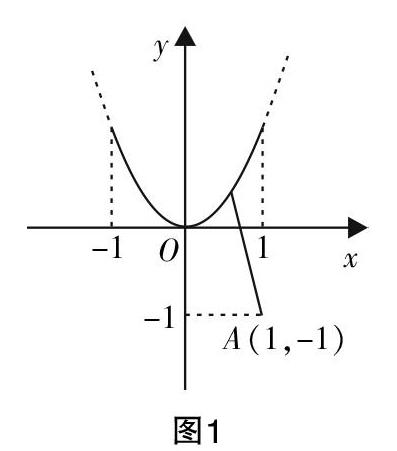
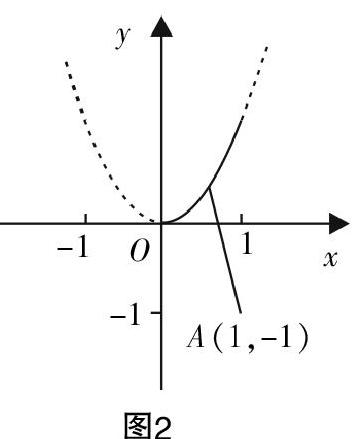
生2：我是利用数形结合进行解答的，而得出的结果却与生1不同. 首先变形以上式子，可得2m>■. 而■=■，则■为点P（sinθ，sin2θ）与点A（1，-1）的连线PA的斜率kPA. 由于点P位于抛物线弧y=x2（-12-2■，所以m>1-■.

师（点拨）：那么此处的取值为什么不是完整抛物线呢？

生2：因为θ的取值范围. 我想我知道错误的原因了，x的取值范围应改为0

此案例中，看似延迟的评价，其实有着很不簡单的思维过程，执教者正是从创新能力的视角，充分认识到问题的价值所在，在巧妙的点拨和引导下，体现出较强的发展性. 而据观察，生2恰好在教师的“留白“之处形成了自主思考和建构.

思维求异，生成创新能力

求异思维的培养需在“创造”中得以实现，因此，在数学教学中，教师需高标准地设计出激发学生求异思维的练习，从而培养学生的创新和创造能力，引导学生爱思、多思、乐思、善思，激发他们主动学习的精神. 而一旦学生的思维能力提升了，智力得到了开发，创新能力势必得到相应的提升.

例4：已知a>0，b>0，m>0，b>a，求证：■>■.

教材中呈现以下解题方法：因为a，b，m∈R+，若要求证■>■，只需求证（a+m）b>a（b+m），也就是证明bm>am，因此只需证明b>a，而根据题设b>a，所以■>■.

有学生立刻提出不同解法，可以借助“浓度问题”进行求证：设一溶液的重量是b，溶质的重量是a，在加入一定数量的溶质m后，该溶液的浓度则会变大，因此得证. 教师首先对这位学生的创造性想象和合理想法表示肯定，而后说明该论述仅仅是以实例对结论的正确性进行解释或阐述，在证明中不可用. 从本题的构思来看，学生求异思维的展现就是本课例的最大亮点，通过求异思维将学生的创新能力推向更高.

总之，创新能力应当是核心素养在数学学科中的具体化，落实到具体的数学教学中，也就是指教师需充分挖掘知识传递过程中的价值，将知识内容的载体作用一览无遗，既要体现素养指向中的学习能力，又需展现数学学科性的数学抽象和数学思维[3]■. 而培养学生的创新能力不是一蹴而就的，离不开日积月累的培养和塑造，这就对我们的课堂教学提出了更高的要求，需要我们教师钻研教材，创新教学方法和策略，从培养学生多种思维能力着手，循序渐进地进行引导，并具体落实在每一节课的具体教学中，有针对性地进行训练和培养.

参考文献：

[1]  耿克非. 培养学生的创新思维能力[J].安徽教育，2004（11）.

[2]  刘会金，林艳. 创新课堂教学设计 突出数学本质内涵——对“中心对称图形”教学设计的思考与评析[J].中国数学教育（初中版），2013（10）.

[3]  任克程. 浅谈中学数学教学中如何培养学生的创新思维能力[J]. 读与写（教育教学刊），2010（07）.