一节递进式问题串的高三数学探究课

吴华波

[摘  要] 高三学生基础较好，已经掌握导数的概念、导数的运算以及导数的基本应用，能够用导数的性质解决初等函数的单调性问题，能利用导数的性质确定简单的含参变量函数的取值范围. 文章以苏教版高三数学一轮复习课《利用导数研究函数的性质》为例，从递进式问题串层层推进课堂教学，提升学生在理解应用导数解决函数单调性性质方面的关键能力.

[关键词] 高三数学;探究课;递进式问题串

教学过程回顾

1. 预习反馈

问题1：对于区间（a，b）上的函数f（x），f ′（x）>0能得到什么？

生：f（x）在（a，b）上单调递增.

问题2：f（x）在（a，b）上单调递增的充要条件是什么？

生：f′（x）≥0在区间（a，b）上恒成立且不恒等于零.

通过求导，可以解决曲线的斜率、求曲线的切线方程，以及利用导数研究函数的单调性，求函数的极值与最值. 还可以利用导数确定参数的取值范围，讨论方程的根和证明不等式，其实质仍然是转化为函数的单调性和极（最）值问题. 例如：

2. 互动释疑

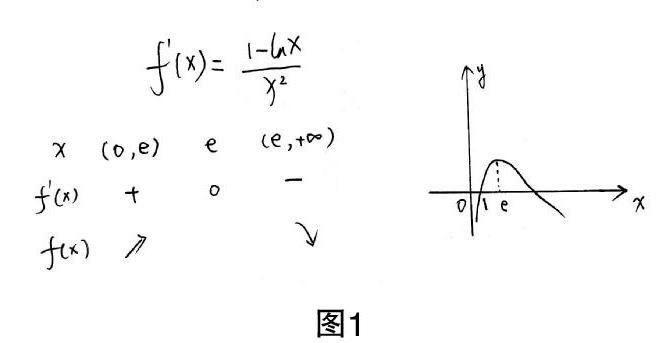
问题3：请讨论函数f（x）=■的单调性，并指出其有几个零点.

学生1：定义域是（0，+∞），求导得单调性，作出如图1的大致图像，因此有两个零点.

学生2：上面同学作图有问题，当x∈（e，+∞）时，函数值都是大于0的，图像不会与x轴有交点，？摇因此该函数只有1个零点.

问题4：已知函数f（x）=lnx+■，求函数f（x）在区间[1，e]上的最值.

通过运算，学生均能正确完成.

问题5：已知函数f（x）=lnx-■（m∈R），求函数f（x）在区间[1，e]上的最大值.

图2、图3是学生自己完成的两种较为典型的解题过程，根据m的取值范围进行了分类讨论，均得到了正确的结果.但大部分学生用图2的做法，做到分类3的时候较为烦琐. 仔细观察发现分类1、2也完全是3的一部分，于是很纠结到底要不要舍弃1、2两类的讨论，在此花费了较多的时间去犹豫和思考.

展示了两种解法后，让采取图3做法的学生做了解释，他说此函数的单调性虽然受到m的影响，但是，通过分析分子x+m在x∈[1，e]上的特性，分子全正（f（x）增），全负（f（x）减），先负后正（f（x）先减后增），根据f（x）的单调性求最大值运算的结果，实际是比较两端f（1）和f（e）的大小，反向得出参数m的取值范围.

问题6：已知函数f（x）=lnx-■（m∈R）在区间[1，e]上取得最小值4，求m的值.

学生开始根据问题5的过程进行了思考，因为本题是直接给出最小值求参数，所以还是利用导函数f′（x）=■对其单调性进行讨论. 此时有了图2求解过程经验的学生，易得到结果，根据图3来解决本问的学生，速度则明显慢了许多.

3. 归纳总结

围绕函数f（x）=■这一比较热门的函数模型的解决方法，利用导数确定参数的取值范围，讨论方程的根和证明不等式，其实质仍然是转化为函数的单调性和极（最）值问题.

课堂上总体以问题串的设计进行深入探讨，逐渐提供一些具有挑战性的问题，学生有比较地利用了常规方法和常规思维的深入转化，体会极值是函数的局部性质，只能刻画函数在某点处的值及其附近左、右函数值的比较.

数学课堂递进式问题串促能力提升的设计思路

围绕问题串，首先回顾导数工具运用，明确概念，从f（x）=■这一具体的流行函数入手，结合学生能够掌握的数形结合的方法，从几何的角度去探究导数的变化与函数单调性的关系，去认识感知导数对单调性的影响，问题3中的问题串是在前面问题1、2上的深入，可以提高学生对单调性有较高层次了解的兴趣.问题4是将f（x）=lnx与一个具体的反比例函数组合，渐渐向应用层面深入引导，学生解决起来也得心应手. 问题5是将反比例函数中的常数改为参变量，并结合求最值过程中常规思维和特殊思路的应用，感受问题3、4的思维并引领运算，感受运算烘托思维的本位化体验.问题6进一步拔高，体现转化与化归的思想. 整节课给笔者的印象是具有探究性，体现了学生数学素养的不断整合与渗透.

1. 数学课堂问题串的引领性

在知识主线清晰、知识网络明确的前提下，预设教学情景，预设内容要依托教材，但不跳出教材，其目标就是运用函数的单调性求参数的值或取值范围，课堂递进中体现师生互动、生生互动的探究结果，体现出一轮复习的目标：全面、系统、扎实、灵活.

2. 探究能力与思维素养在课堂上的渗透

核心素养在数学课堂上的体验是一个认知、解决、内化的过程，一道题或一堂课不可能就将整个核心全部体现出来.课堂的推进过程中，学生体现出的勇于质疑、勇于探索、理性思维的精神，勇于展现自我、勇于批评与自我批评的能力等，师生之间的相互赏识，教师体现出的人文情怀、德育渗透等，这些都属于核心素养提升的范畴.现行的高考怎么考，一个是考数学的关键能力，另一个是考渗透的德育功能，它是意志品质的考试，是对学生自我定位、自我调整、自我提升的一種体现.

3. 处理好数学素养提升上的三个关系

第一个关系：讲授与引导的关系.对此课堂上较好的处理，都是以引导、探究为主，高三一轮复习的课和高一、高二的课不一样，不是告诉学生这是什么，学到了什么，而是激发学生主动去寻找、参与.

第二个关系：基础与能力的关系.巩固基础是一轮复习中要特别注意的环节，宁可能力先放一放，也要先打下扎实的基础. 尤其是学生在没建立知识网络结构的复习课上，教师要引导学生积极地参与知识网络的建构，这很重要，不管是采用回顾整理知识点的方式，还是由小题带出知识点，都要注重通性通法与基本技能的训练. 能力不是通过讲就拥有的，是教师要舍得给足时间让学生去运算，去经历，去探究，去实践;精讲不是不讲，不是少讲，是“教学生去发现”.

第三个关系：落实与速度的关系.不要过度追求课堂的容量，但也不是说课堂的容量大就是坏事情，这里说的容量是指学生落实下去的容量，不是题目的容量，而是思维的容量.高三复习时间紧张，我们要在保证课堂容量的情况下，适当提升讲授的速度. 如果教师在课堂上面不紧不慢，学生会在潜意识里缺乏一种压迫感. 我们经常遇到这样的情况：学生平时作业能慢慢做出来的题，但一到考试的时候就不知该如何下笔.从这里，我们也能感受到，高三复习时，需要给予学生一定的压迫感，有意识地锻炼学生做题的速度，提高学习效率.

用问题串设计高三数学探究课的原则

1. 突出课堂教学的主导与主体

教师注重学生的修正与学生的评价，这是教师主动带领下完成的，教师在知识点的整合与整理上的作用不可替代，探究的方向是可控的，是层层递进的，学生的展示具有可评价和可对比性，学生的主体地位需要进一步凸显.

2. 突出结合教材的指导性地位

教材上面给出的要点比较简洁，整理的例子与考题必然是围绕实例展开的，好比说函数零点这一块，导数对单调性的阐述这一块，假若只看教材，除了定理精确的表述，教材上经常是给一个示例或者思考进行补充，需要紧扣这些思考进行深化解释，给出正确的表述，印象会更深刻. 一轮复习到底是做后教，还是教后做，还是边做边教，这点是要根据教材的内容不同、难度不同而灵活处理的，不是说每一堂课都要按照什么一个顺序去处理.

3. 难度的把握不等同于素养的高低

一轮复习到底到哪个难度，并没有一个具体的标准.有的教师说最后这个题的难度高了，有的说这个难度能够接受，实际上，教师需要把握的是该题适不适合自己的学生，能达到学生能想能写的难度就是合适的难度，当然对于各个学校的实际来说，是可以酌情考虑的.