基于模糊收益率的分散化投资组合调整策略
2020-09-26杨兴雨刘伟龙井明月
杨兴雨,刘伟龙,井明月,张 永
(广东工业大学 管理学院,广东 广州 510520)
正所谓“不要把所有鸡蛋放在同一个篮子里”,为了规避风险,投资者往往把资金分散地投资在多个资产上。假设资产收益率为随机变量,分别用资产组合的均值和方差度量其收益和风险,Markowitz[1]提出了均值-方差(MV)投资组合选择模型,为现代投资组合理论奠定了基础。随后,学者们对MV模型进行广泛的推广[2-5]。
随机投资组合模型利用随机变量刻画资产收益的不确定性,并通过历史数据的统计信息来确定收益率的随机分布。然而,在实际的金融市场中投资决策受到许多非概率因素的影响,如专家观点、投资者情绪等,这些不确定性因素在很大程度上具有模糊性。因此,众多学者开始基于Zadeh[6]提出的模糊集合理论研究模糊不确定环境下的投资组合问题。Carlsson等[7]用可能性均值和可能性方差度量资产组合的收益和风险,提出了一个效用最大化的模糊投资组合模型。刘勇军等[8]考虑现实投资约束,提出了一个以资产组合收益和偏度最大化,以资产组合风险、不确定性和模糊性最小化为目标的多准则模糊投资组合模型。Yue等[9]提出了一个综合考虑投资组合下半方差风险和下半绝对偏差的多目标模糊投资组合模型。王灿杰和邓雪[10]提出了一个带融资约束的多目标模糊投资组合模型,并设计了一个改进的多目标粒子群算法进行求解。宋健和邓雪[11]针对模糊不确定的证券市场提出了一个均值-方差投资组合模型,并综合粒子群算法和人工鱼群算法设计了一个混合智能算法进行求解。
以上模糊投资组合模型假设资产的收益率为模糊变量,在实际应用中还需要对模糊分布的参数进行估计。考虑到线性隶属函数在处理上的便利性,许多学者利用三角模糊数或梯形模糊数来拟合资产的模糊收益率[12-14]。针对模糊收益率的拟合问题,Zhang等[15]提出了一个模糊频率估计法。该方法通过统计和分析历史收益率在事先划分好的各个区间上的频数来确定模糊收益率的参数。Vercher等[16]提出将资产的历史收益率进行排序,然后基于历史收益率的特殊分位点来确定模糊收益率的参数。以上两个简单的估计方法在操作过程中都带有较强的主观性,如划分区间和分位点选择问题,因此在实际应用中不同投资者可能得到差异性较大的结果。此外,以上方式只通过对历史数据的简单分析来确定模糊收益率的参数,并没有考虑专家的观点。
众所周知,在传统的随机投资组合问题中可以通过分散化投资来降低投资风险,因而在追求风险最小化时往往会构建一个分散化的投资组合。然而,在模糊投资组合问题中,传统的风险测度往往在所有资金集中于风险最低的资产上时取得最小,因而传统的投资组合模型往往获得一个集中投资于少数资产的投资组合,这与实际的投资组合管理经验是相悖的[17]。针对传统模糊投资组合模型过度集中投资的缺陷,主要改进措施有2种:(1) 引入投资比例上下界约束[8,18]。该方法处理简单,然而分散化的效果并不理想。(2) 引入比例熵的概念作为资产组合的分散化测度[19-21]。资产组合的比例熵在均匀投资时取得最大值,因而未能体现各个资产之间的差异性。
本文研究模糊环境下考虑交易费用和基数约束的投资组合调整问题。首先,将资产的收益率视为梯形模糊数,并基于资产的历史收益率和专家观点提出一个模糊收益率拟合模型来确定资产模糊收益率的参数。其次,通过提出一个资产组合的分散化测度,以资产组合收益率的可能性均值作为其收益测度,资产组合收益率的下半方差作为其风险测度,构建模糊均值-下半方差-分散化的多准则投资组合调整模型。然后,设计一个改进遗传算法求解所提出的模糊收益率拟合模型及投资组合调整模型。最后,通过真实股票数据对所提出的策略进行实例分析,说明策略的有效性。
1 预备知识
为了便于叙述,首先介绍本文所涉及的模糊数学的相关知识。
定义1[6]若模糊数A的隶属度函数具有式(1)的形式

其中α,β >0 ,L,R:[0,1]→[0,1]为单调不增的连续函数且满足L(0)=R(0)=1 和L(1)=R(1)=0,则称模糊数A 为L R型模糊数。

引理1[22]设A1=(a1,b1,α1,β1)和 A2=(a2,b2,α2,β2)为梯形模糊数。对于任意实数λ ∈R,有
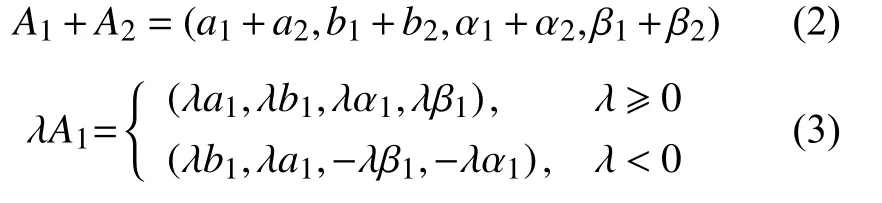
定义2[23]模糊数A的 可能性均值定义为其γ -截集中点的加权平均数,即

定义3[24]模糊数A的可能性上半方差定义为其γ-截集的右端点与其可能性均值之间距离的平方的加权平均数,即
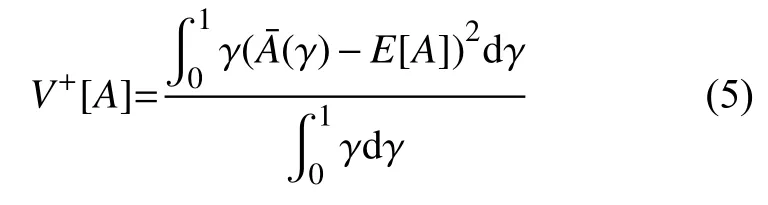
定义4[24]模糊数A的可能性下半方差定义为其γ-截集的左端点与其可能性均值之间距离的平方的加权平均数,即

定义5[24]模糊数A的可能性方差定义为其可能性上半方差和下半方差的平均数,即

特别地,梯形模糊数A=(a,b,α,β)的可能性均值、下半方差和方差分别为
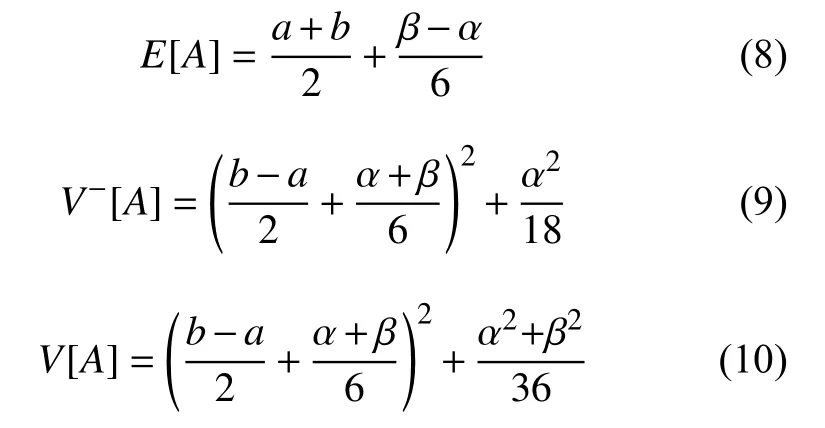
2 模糊收益率拟合模型
在进行投资决策时,首先需要估计各个风险资产的模糊收益率。考虑到线性隶属度函数便于处理,本文使用梯形模糊数来拟合资产的未来收益率。首先,通过模糊频率量化资产收益率基于历史数据的可能性。其次,考虑到专家观点对于预测资产未来收益具有比较大的价值,综合分析和讨论专家在对所投资资产未来表现的观点,将资产的未来收益率量化为一个三角模糊数。最后,通过整合历史数据信息和专家观点,建立一个模糊收益率拟合模型,将资产的收益率估计为一个梯形模糊数。

x在数据集 rh中出现的模糊频数。
模糊频数f(x)表示资产的历史收益率取值在x 附近的次数,如图1所示。例如,图中 x0点的模糊频数为2.2。

图1 模糊频数的计算方法Fig.1 Calculation method of fuzzy frequency




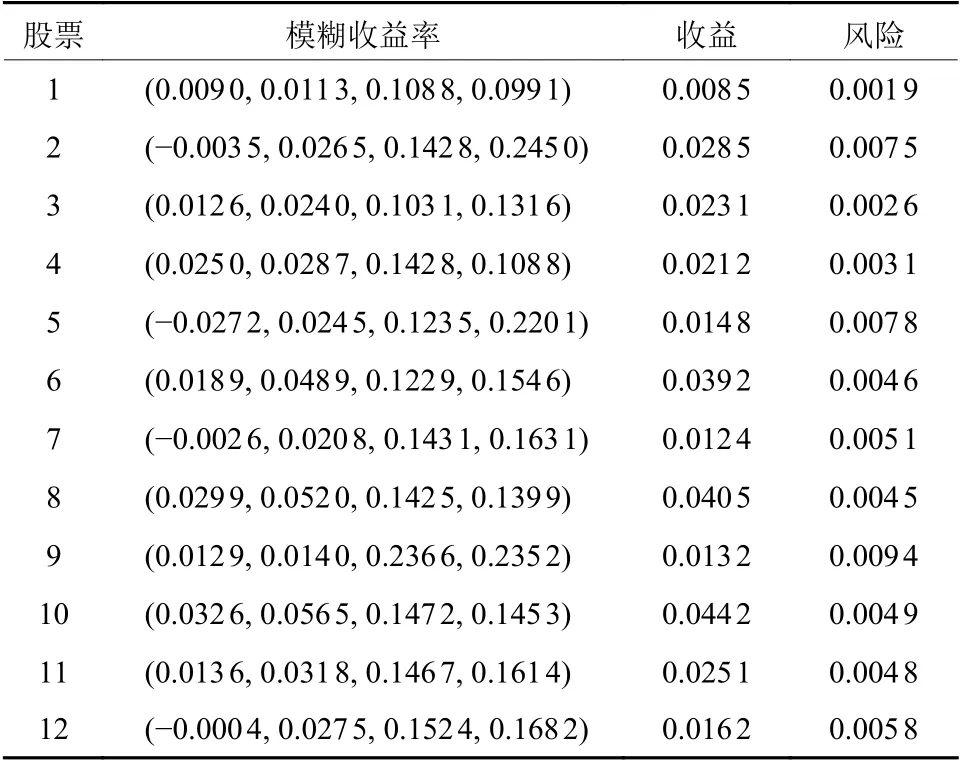
表3 所选股票模糊收益率的拟合结果Table 3 The fitting result for fuzzy return rates of the selected securities

表4 模型P 4 ~P 6的最优投资组合Table 4 Optimal portfolios for model P4 ~P6


下面,根据历史数据和专家观点估计一个资产的模糊收益率,假设其为梯形模糊数r=(a,b,α,β),隶着,通过测试集的数据比较各个投资组合策略在未来半年的实际表现。以每个月最后一个交易日为节点,记录表5中5个策略在测试集中的财富累积情况,结 果如表6所示。

表5 5个模型的最优投资组合Table 5 Optimal portfolios for the five models

表6 5个模型所构建策略的累积财富Table 6 Cumulative wealth for the investment strategies obtained by the five models
由表5可知,本文所提出的FMSVD模型与传统的Markowitz的MV模型可以构建一个较为分散化的投资策略,而传统模糊投资组合模型FMSV和FMSAD所构建的投资策略集中投资于少数几只股票上。可以看到,本文提出的策略可以构建结构合理的投资组合。从表6可以看出,与其他模型相比,本文提出的FMSVD模型在测试集中的财富累积状况一直维持在较高的水平。因此,本文所提出的策略在实际应用中具有较好的表现。
6 结论
本文研究了模糊环境下考虑交易费用和基数约束的投资组合调整问题。首先,基于历史数据和专家观点,通过建立一个模糊收益率拟合模型,确定了各个资产收益率的模糊分布。其次,考虑到传统模糊投资组合模型所构建的投资策略往往集中投资于少数资产,提出了一个模糊均值-下半方差-分散化投资组合调整模型。然后,根据投资者对各个目标的偏好将所提出的多目标规划模型转化为单目标规划模型,并设计了一个改进的遗传算法求解所建立的模型。最后,通过实例分析说明了所提出的策略可以实现较高的收益,较好地满足投资者的分散化要求,具有较强的实用性。在实际投资过程中,影响投资决策的因素和约束很多,本文仅考虑了交易费用与基数约束。因此,考虑更全面的市场因素和现实约束的模糊投资组合调整问题有待进一步探讨。
