6061铝合金铣削工艺参数多目标优化

2020-09-26唐超兰

广东工业大学学报 2020年5期

唐超兰，谢义

（广东工业大学机电工程学院，广东广州 510006）

铝合金零件具有质量小、强度高、加工性能好等优良性能，被广泛应用于航天、医学、汽车等领域[1-2]。加工工艺参数的选择是影响铝合金零件质量的关键因素，同时也能有效提高机床使用寿命、加工效率和成品率，降低原材料和能源消耗，从而降低制造成本，实现绿色制造。影响铝合金零件铣削加工精度的因素有加工工艺方案、刀具参数、刀具路径、装夹方案等，其中工艺参数的选择一直是一个难题，其对铣削力、切削温度、刀具寿命等都有重要影响。然而，许多数控加工企业还在凭经验、参考手册或通过试切法来选择切削参数，往往难以实现高效率、高精度的最优化[3]。如果铣削工艺参数选取不合理，不仅难以保证零件加工精度、成本，而且可能因切削力过大等原因造成刀具损坏，降低机床的使用寿命。因此，研究铝合金铣削加工性能，优化工艺参数，对提高加工效率和加工质量，降低制造成本，提高设备使用寿命，实现绿色制造具有重要的应用价值。

在铝合金铣削加工过程中，采用较大的切削工艺参数可以缩短加工时间，但会加剧刀具磨损，降低表面质量。由于刀具快速磨损而频繁换刀，将影响加工效率并提高加工成本。表面质量恶化会降低零件的材料力学性能，可能使零件在使用过程中失效，从而造成安全事故。因此，铝合金的高效铣削加工需要实现材料去除率、加工成本以及表面质量三者之间的平衡，其本质上属于多目标优化问题。目前，已有学者在铣削加工效率、加工精度和成本控制等方面获得了许多研究成果。黄晓明等[4]对7 050-T7451铝合金高速铣削进行了正交实验，分析了铣削参数对表面粗糙度的影响规律，得到了铣削参数对表面粗糙的影响显著性；丁涛等[5]基于正交试验，使用表面粗糙度经验公式，对6 061-T651铝合金铣削工艺参数进行了优化；伍文进等[6]对6 061铝合金进行了铣削单因素试验和正交实验，分析了主轴转速、进给速度和切削深度对表面质量的影响规律；Ajith等[7]使用神经网络和田口灰色关联分析对铝基复合材料铣削参数进行了多目标优化，并证明人工神经网络(Artificial Neural Network, ANN)模型比回归模型预测精度更高；姚倡锋等[8]通过铣削试验发现铣削速度和每齿进给量的比例关系会严重影响加工表面的形貌；Li等[9]使用NSGA-II算法对Ti6Al4V铣削工艺参数进行了多目标优化，优化结果有利于增加刀具寿命，降低表面粗糙度；王立新等[10]进行了高强度铝合金干式铣削试验，试验结果表明表面最佳工艺参数组合为高切削速度、中等切削深度和较小进给量；谢黎明等[11]使用Deform-3D软件仿真分析了铝合金铣削参数对表面粗糙度的影响，并对其进行了实验验证，结果表明背吃刀量对表面粗糙度影响最大；邓朝晖等[12]以刀具寿命和零件表面质量为约束条件，以能量效率最高、碳排放最低和材料去除率最高为多目标优化目标，使用信噪比方法将多目标优化问题转化为单目标优化，对铣削参数进行了优化。

通过文献分析可知，在铣削工艺参数选择时要综合考虑刀具参数、机床性能、铣削参数等因素，但上述研究多是选择3或4个工艺参数进行优化，考虑不够全面。因此，本文在前人的研究基础上，以6 061铝合金铣削为研究对象，以主轴转速、进给速度、轴向进给量、径向进给量和刀具直径为实验因素，设计了五因素五水平正交实验，建立了6 061铝合金铣削多目标优化模型，使用gamultiobj函数对优化模型进行求解，得到了优化后的铣削工艺参数，能有效提高加工效率和加工质量，降低制造成本，实现绿色制造。

1 铣削试验设计与分析

以6 061铝合金为研究对象，经过大量研究与分析可知，评价Al6061铣削加工性能指标主要有加工效率、表面质量和加工成本等，主要体现在切削力大小、加工质量、刀具寿命和材料去除率等性能指标，在加工工艺条件一定情况下，影响这些指标的主要因素包括刀具直径、切削速度、铣削深度、进给速度和铣削宽度5个参数，因此，通过试验的方法研究不同加工参数对性能指标的影响。

在试验时选用硬质合金刀具，前角45°，后角5°，数控机床使用台群精机T-500数控加工中心，使用Bruker GTX型白光干涉仪获取表面粗糙度值，以单位时间内铣削材料体积作为材料去除率，以表面粗糙度衡量加工表面的表面质量。为减少试验次数，选用多因素正交试验设计方法进行样本布点，采用L25(55)正交表进行试验，得到25组试验结果，如表1所示。

2 表面粗糙度预测模型

由于表面粗糙度与铣削参数之间的关系为非线性映射关系，在建立非线性映射关系的研究上，目前通常使用神经网络等人工智能方法。神经网络在工程问题中得到越来越多的应用，其中在表面粗糙度的预测中应用最为广泛的是反向传播神经网络(Back-Propagation Network，BP神经网络)[13]。通过对大量文献分析得到遗传算法(Genetic Algorithm，GA)优化的BP神经网络预测模型(GA-BP预测模型)相比BP神经网络预测模型和线性回归预测模型，预测精度相对较高[14]。因此，本文采用GA-BP预测模型建立铣削参数与表面粗糙度之间的非线性关系。

2.1 GA-BP铣削表面粗糙度预测模型

2.1.1 BP神经网络

BP神经网络是Rumelhart和McClelland于1986年提出的一种多层前馈网络的误差反向传播神经网络学习算法[15]，其由输出层、隐含层、输入层和权值与阈值组成。在隐藏层中，可以根据层数将其分为单个隐含层和多个隐含层。多隐含层与单隐含层相比，泛化能力更强，预测更准确，但是训练时间相对较长。在决定隐含层数目时，应考虑网络的精度和训练时间。对于简单的映射关系，当满足网络精度时，应该选择单个隐含层以加快训练速度。对于复杂的映射关系，首选多层隐含层数目以提高预测的精度。实验表明用一个3层的BP神经网络可以构建一个从任意的a维输入层到b维输出层的映射。因此，在本文中，使用单隐含层结构，其包括输入、输出神经元和隐含层神经元。

表1 铣削正交试验结果Table 1 Milling orthogonal test results

通过对表面粗糙度的神经网络预测模型研究表明[16-17]，隐含层的神经元个数对模型预测精度有重要影响。因此，在确定网络层的结构后，应该选取合适的隐含层神经元数目，输入、输出神经元的数目由训练数据决定。关于隐含层神经元数目的选取，目前还没有相应的数学理论，一般根据工程经验或试错法进行选取。隐含层神经元数目也可根据经验公式(1)选取。经过反复试错后发现m取5时精度最高。其中，m是隐含层神经元个数，n是输入层神经元个数，l是输出层神经元个数，α是1～10的常数。

2.1.2 基于遗传算法的BP神经网络参数优化

理论上，如果有足够多的训练数据，并且隐含层节点选择合理，BP神经网络可以逼近任何非线性映射关系。但BP神经网络的缺陷是容易陷入局部最优，网络训练之初，神经元的权重与阈值都是随机确定的，因此训练的网络不够稳定。经遗传算法优化后，可得到较好的初始权值和阈值，进一步提高神经网络的预测性能。GA-BP神经网络表面粗糙度预测模型的实现流程如图1所示。

步骤1：确定BP神经网络的拓扑结构。

步骤2：种群初始化，并对初始权值与阈值进行基因编码。

图1 GA优化BP神经网络流程图Fig.1 Flow chart of the BP network optimized by GA

步骤4：选择。选择轮盘赌法进行个体择优，如式(4)所示。

步骤5：交叉。以一定概率选择种群个体进行交叉。

步骤6：变异。以一定概率对种群个体和基因位置进行随机变异。

步骤7：重复进行步骤2～6的操作，直到优化参数满足要求。

2.2 预测模型有效性验证

在训练模型之前，为了消除输入和输出之间的数量级差异，必须使用标准化方法对每个输入和输出进行数据预处理。归一化和反归一化的一般方法如式(5)和式(6)所示[18]。

其中，x是待归一化数据，X是归一化后的数据，xmax和xmin是待归一化数据中的最大、小值，b和a是目标归一化区间的上、下限。

使用表1中的试验数据进行GA-BP铣削表面粗糙度预测模型的训练，遗传算法优化训练结果如图2和图3所示，均方误差值与适应度值在迭代次数达到220次迭代后趋于稳定。

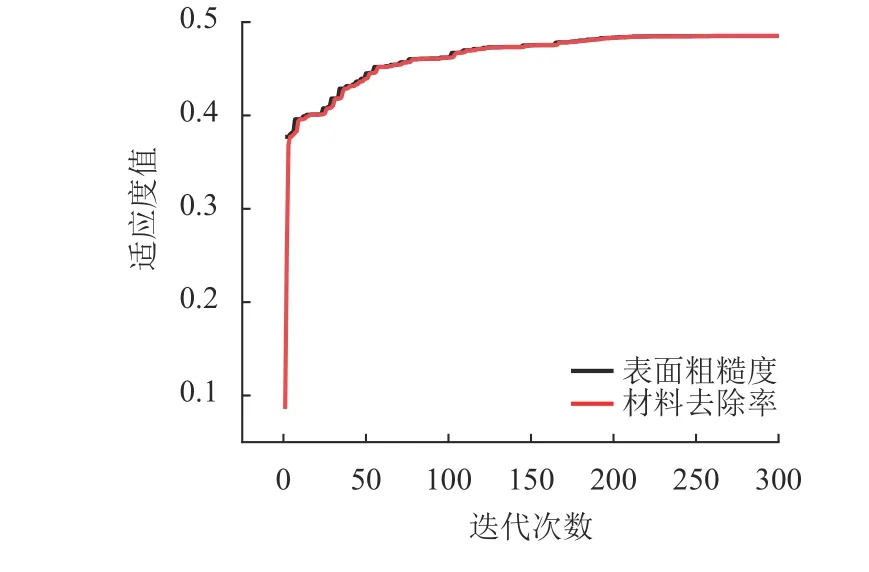
图2 适应度函数值变化Fig.2 Fitness function value change

图3 遗传算法均方误差Fig.3 Genetic algorithm mean square error

为了验证模型的预测精度，另外做了5组实验，实验结果如表2所示。从验证试验结果可以分析出，GA-BP预测模型相对比BP神经网络预测模型和支持向量机(Support Vector Machine, SVM)预测模型精度较高，且最大误差仅为5.76%，因此，GA-BP预测模型可以用于铣削表面粗糙度的预测。

3 铣削工艺参数优化

3.1 基于NSGA-II算法的gamultiobj函数

基于NSGA-II算法的gamultiobj函数是MATLAB软件中开发的一种多目标优化遗传算法，其使用快速非劣排序、新的多样性保持策略使得计算效率大大提高，同时引入拥挤比算子，使计算的Pareto前沿分布更均匀[19]。

3.2 优化问题

3.2.1 优化变量

构造优化变量x=(x1,x2,x3,x4,x5)，其中x1,x2,x3,x4,x5分别表示刀具直径(D)、主轴转速(n)、径向进给量(a)、轴向进给量(b)、进给速度(v)。

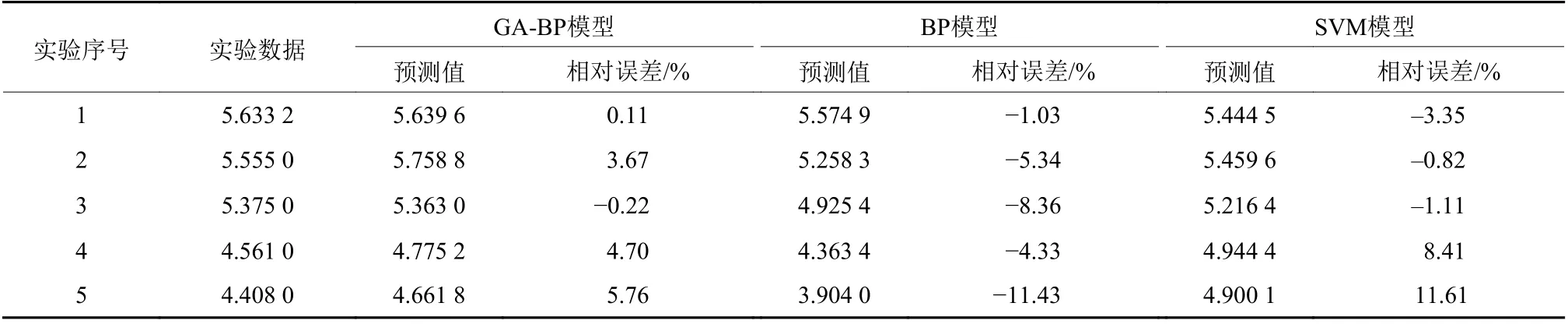
表2 表面粗糙度预测值与实验数据对比Table 2 Prediction compared with experimental data of surface roughness

3.2.2 约束条件

铣削工艺参数优化的约束条件需要综合考虑机床、刀具、加工参数等对加工质量的影响，本文选取的约束条件如下：

刀具直径D，mm，4 ≤D≤ 12；主轴转速n，r·min-1，9 000 ≤n≤ 13 000；径向进给量a，mm，0.1 ≤a≤ 0.3；轴向进给量b，mm，1 ≤b≤ 8；进给速度v，mm·min-1，900≤ v≤1 300。

3.2.3 目标函数

本文旨在提高加工精度和加工效率，因此选取表面粗糙度和材料去除率作为优化目标。

表面粗糙度目标函数如式(7)所示。

其中，A是输入变量矩阵，net是训练后的GA-BP表面粗糙度预测模型，y是预测值。

材料去除率目标函数如式(8)所示。

综上所述，铣削参数多目标优化的数学模型如式(9)所示。

显然，这是一个多变量、非线性约束的多目标优化问题。

4 优化结果分析

使用MATLAB中以NSGA-II算法为基础开发的gamultiobj函数对上述多目标优化问题进行求解，得到的Pareto前沿如图4所示。

图4中，Pareto前沿变化趋势表明，在AB段，材料去除率相对表面粗糙度变化速率大；在CD段，表面粗糙度相对材料去除率变化幅度大；在保证表面粗糙度和材料去除率的同时，BC段的Pareto点构成的集合是期望解集。提取BC部分Pareto解，如表3所示。

图4 铣削参数多目标优化Pareto前沿Fig.4 Multi-objective optimization of milling parameters

分析Pareto解集可以得到以下规律。

(1) 优化后的各铣削参数之间差别较小，其对应的表面粗糙目标函数差别较小，材料去除率目标函数有较小波动，这表明在试验铣削参数的取值范围内，参数变化对表面粗糙度和材料去除率的影响一致。

(2) 主轴转速、轴向进给量和进给速度对表面粗糙度和材料去除率的影响显著且接近上限，刀具直径和径向进给量对表面粗糙度和材料去除率影响较小且接近下限。

(3) 合理提高主轴转速、减小径向进给量，会较大降低表面粗糙度并且保证一定的材料去除率。

5 结论

建立了以材料去除率和加工表面粗糙度为优化目标的多目标铣削参数优化模型，使用基于NSGAII算法开发的gamultiobj函数对模型进行求解，得到较优铣削参数范围。

综合考虑加工效率和加工精度，应选择较高主轴转速、较小径向进给量和进给速度，合理增加轴向进给量。高速铣削6 061铝合金，推荐选用铣削参数：主轴转速12 000～13 000 r·min-1，径向进给量0.19～0.21 mm，进给速度1 272～1 300 mm·min-1，轴向进给量6～8 mm，刀具直径4 mm。