极端应变率下钨孔洞演化及其力学响应的分子动力学模拟

百晓丹，陈逊，马运柱，刘文胜，梁超平

极端应变率下钨孔洞演化及其力学响应的分子动力学模拟

百晓丹，陈逊，马运柱，刘文胜，梁超平

(中南大学 轻质高强国家重点实验室，长沙 410083)

极端应变率；分子动力学模拟；孔洞；塑性变形；位错

钨及钨合金具有密度大、熔点高和高温强度高等优异性能，是国防军事领域的关键材料之一，也是目前对付装甲目标等的主要动能武器弹芯材料[1]。随着防御工事和武器装备的发展，高超声速飞行器技术及其军事应用成为现今研究的热点[2]。因此，应用于未来高超声速领域的钨及钨合金材料将承受更加严苛的作业环境，如极端应变率等。现有高应变率下的钨及钨合金变形行为研究主要通过Hopkinson拉/压杆[3-4]、轻气炮[5]和爆炸加载[1]等技术实现，应变率范围在102~ 106s−1。近年来，随着激光能量的提高和美国等国家强激光装置对学术界的开放，科学家得以通过激光驱动撞击实验，揭示材料在更高应变率106~1010s−1下的塑性行为[6]。在激光驱动撞击的极高应变率下，材料出现与低应变率下截然不同的塑性变形机制，如随应变率升高，塑性变形由位错滑移为主转变为孪晶变形为主；随应变率进一步升高，材料又发生结构相变或非晶化转变[7]。然而，高应变率使得直接对材料塑性变形行为的观察变得极为困难，使用第三代窄脉冲同步辐射光源能原位观察材料在激光驱动撞击下的晶体结构信息，但无法获得具体的位错运动、孪晶变形以及相变过程[8]。分子动力学模拟可准确纪录原子在飞秒、皮秒尺度下的运动轨迹，已被证明是研究材料在极端应变率下变形行为的最有效手段[6]，如ZEPEDA- RUIZ[9]和WEHRENBERG等[10]通过分子动力学预测了金属钽在极端应变率下位错到孪晶的转变过程，并通过实验验证了模拟结果。钨及钨合金通常采用粉末冶金方法制备，存在大量孔洞，而孔洞演化又是材料在极端应变率下碎裂失效的主要原因[6]。为此，本文作者采用分子动力学模拟来研究极端应变率(108~1011s−1)下单晶钨中孔洞的演化规律，获得孔洞尺寸和应变率对钨动态力学性能的影响，并从原子尺度揭示孔洞演化的塑性机理，为钨合金在极端应变率下的应用提供理论指导。

1 模拟方法

采用LAMMPS软件进行分子动力学模拟[11]，通过嵌入原子方法描述钨原子间的相互作用[12−15]。孔洞模型是在尺寸为48×48×48(为钨的晶格常数，=0.316 5 nm)的体心立方(BCC)钨单晶块的中心掏半径分别为12，15，17和19的圆孔(为钨的原子半径，=0.137 0 nm)，具体的模型细节列于表1。对所建立的模型，首先通过共轭梯度法静态优化其结构和原子位置，并进一步通过等温等压系综(isoth- ermal-isobaric ensemble, NPT)获得优化后的结构在300 K下的平衡结构。其中时间步长设置为0.001 fs，运行50 000步后的孔洞结构如图1所示。最终，通过在正则系综(canonical ensemble, NVT)下对模型的X轴(对应[100]晶向)以恒定应变率(108~1011s−1)施加体积变化来获得体系的应力状态，模拟沿X轴压缩到初始长度的1/4时终止。在模拟过程中，通过Langevin控温器来保持体系温度为300 K。为了获得变形过程中的原子信息，根据不同应变率来选取模拟的时间步长(2~0.5 fs)，以保证相同应变间隔下的原子信息一致。变形后的缺陷通过OVITO软件中的位错提取算法(dislocation analysis, DXA)和公共近邻分析(common neighbor analysis, CNA)进行表征[16]。

表1 不同孔径模型的结构参数

Note:is the radius of tungsten atom,=0.137 0 nm; ais the lattice constant of tungsten, a=0.316 5 nm.

图1 等温等压系综(NPT)300 K弛豫后的孔洞结构

2 结果与讨论

2.1 孔洞尺寸效应

对不同孔径的孔洞模型进行计算，结果表明孔洞的大小不会影响钨的弹性和塑性变形行为。图2所示为无孔洞的理想单晶模型和具有不同尺寸孔洞的模型在应变率为108s−1时的应力−应变曲线。从图中看出，在无孔洞的理想状态下，钨的屈服强度为58.5 GPa，孔洞的存在使得屈服强度急剧降低，孔半径=12时屈服强度下降至29.0 GPa。随孔径增大，屈服强度进一步降低，在=19时屈服强度降至26.0 GPa。产生这一现象的主要原因是孔洞处产生的高应力集中和低的位错启动力。封闭孔的应力集中计算公式为[17]：

式中：σmax为孔洞处的最大应力；σ¥为远离孔洞处的应力；R为孔的半径。由式(1)可知孔洞处的应力集中随孔径增大而增加，R=19r的孔洞处的应力集中程度较R=12r孔洞处的增加25%，这是导致钨的屈服强度下降的主要原因。孔洞处高的应力导致钨的塑性变形提前发生，无孔洞的完美晶体在应变ε=0.068时发生屈服，而在含有R=12r的孔洞时，在ε=0.039就已经发生塑性变形。

从应力−应变曲线的弹性阶段看出，孔洞的存在也导致钨的弹性模量减小，并且随孔洞尺寸增大，弹性模量进一步降低。从原理上看，弹性模量是材料的本征属性，反映了原子、离子或分子之间的键合强度。中心对称参数(centrosymmetry parameter, CSP)的计算公式为[11]：

式中：为成键数；e为原子平衡间距；为受力面积；d/d为原子间势能的一阶导数。从式(3)可知弹性模量与成键数呈线性关系。表2所列为模型弛豫前断1~4根键时的CSP值和总断键数，式(3)中的成键数等于无孔洞时的总成键数total减去有孔洞时的断键数broken，即=total−broken。因此弹性模量与断键数呈线性关系，斜率为负值，即随断键数增加，弹性模量降低。图3所示为弹性模量与总断键数的对应关系，图中的弹性模量由图2中不同孔径的模型弹性变形阶段线性拟合得到。从图中3看出，弹性模量与断键数呈很好的线性关系，随孔洞半径增大，断键数增多，弹性模量由理想致密晶体(断键数为0)的387.05 GPa降低到=19(断键数为21 356)的370.83 GPa。从以上分析可知，内封闭孔洞处的断键导致单晶钨的弹性模量降低。

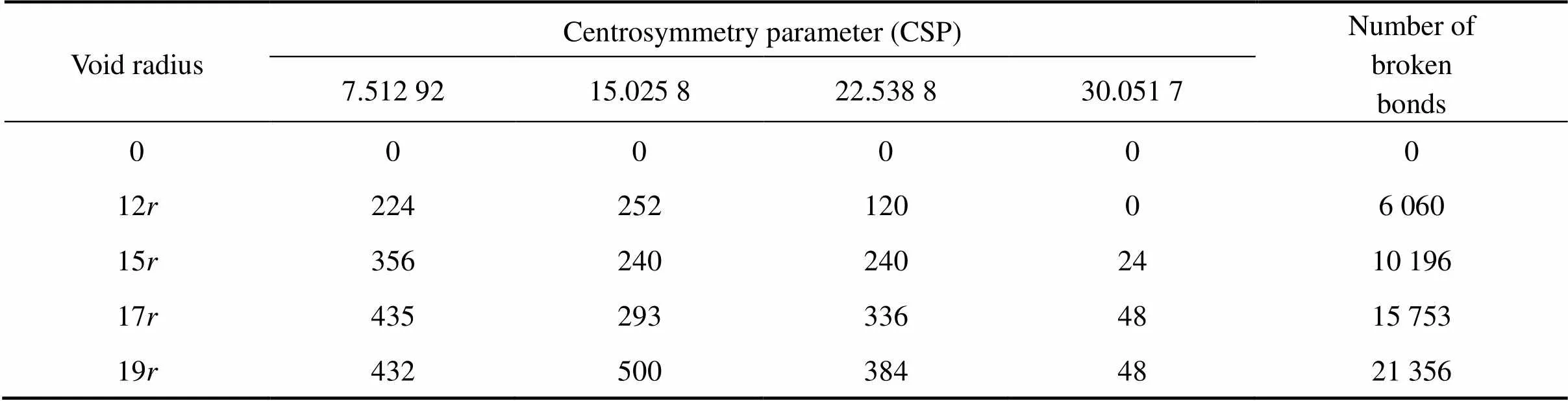
表2 不同孔径的孔洞模型断1~4根键时的中心对称参数和总断键数

图3 含孔洞单晶钨的弹性模量与断裂金属键数量及孔洞半径的关系

2.2 应变率的影响

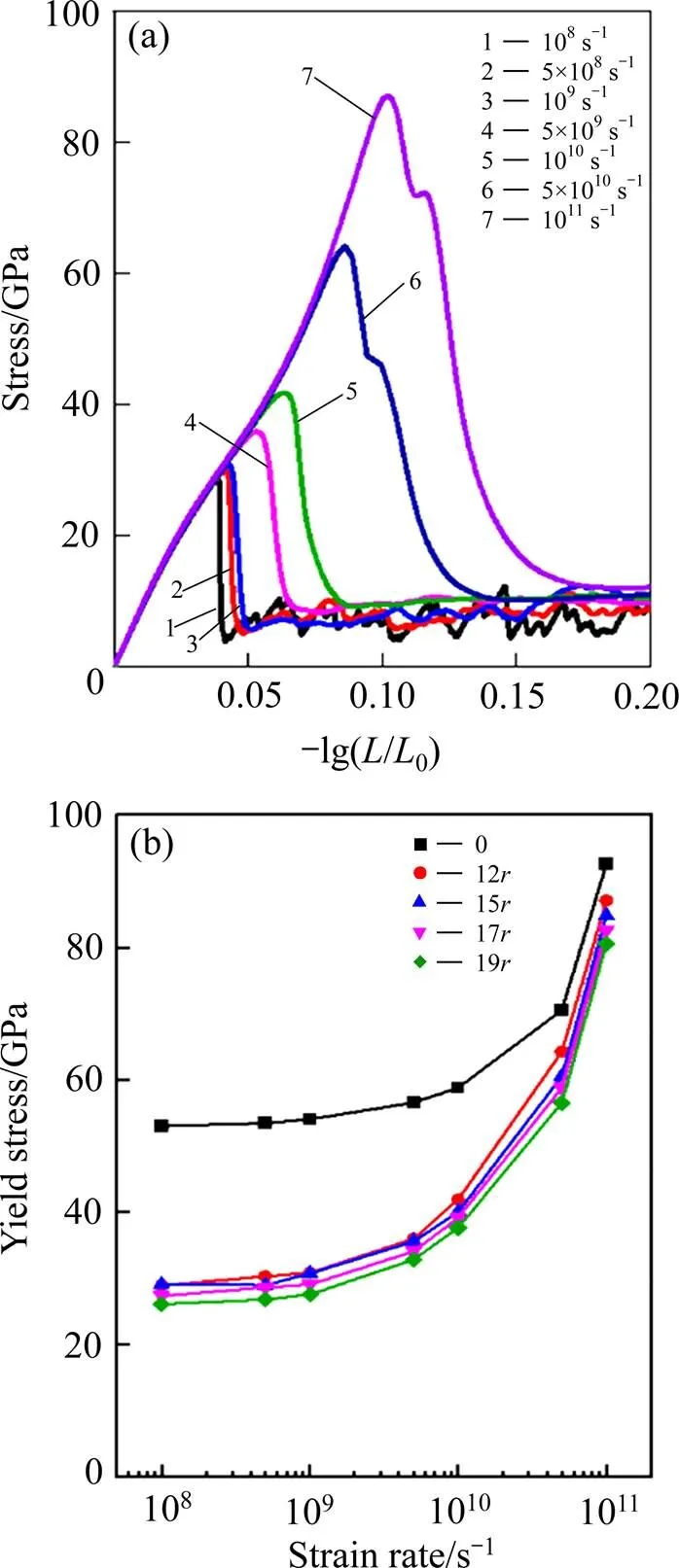
图4 应变率与孔洞半径对钨压缩性能的影响

(a) Stress-true strain curve of tungsten under different strain rates (void radius=12); (b) Yield strength of tungsten with different void radius as a function of strain rate

2.3 孔洞塑性变形机理

为了研究孔洞在应力集中下的变形机理，采用通过位错提取算法和公共近邻分析来研究孔洞形貌变化和缺陷。与实验不同，分子动力学模拟得到变形过程中的原子结构信息，图6所示为典型应力−应变曲线上各点的原子结构信息。从图6看出，在屈服点a时，孔洞沿[100]发生一定的压缩，且位错开始在某些面上形核；压缩进行到b和c点时，一个位错环开始向外发射；到达d点时，第一个位错环完成一次剪切回到孔洞，而其他方向的位错环继续向前发展；不同方向的位错环不断发射和运动，导致孔洞发生不同方向的剪切，最终孔洞坍塌，呈现e点处不规则形状的孔洞，如图6(e)所示。

图5 单晶钨在不同应变率下屈服时的原子结构快照和径向分布函数

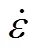
通过对应力矩阵进行晶体坐标系到滑移系转换，得

图6 含孔洞R=12r的单晶钨在应变率108 s−1下压缩变形过程中的原子快照

图7 R=12r孔洞在应变率108 s−1下压缩变形时的位错环结构(对应图6中的c点)

不同{112}面上发射的1/2[111]位错在一定条件下可发生如下位错分解：

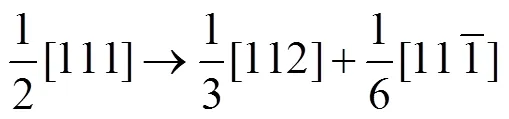
从而在初始滑移面上留下的不全位错，所以当1/2[111]螺位错发生交滑移到相邻的{112}面时，体系中留下一段孪晶。通过位错提取算法分析发现，孔洞处发射位错的伯氏矢量均为1/2[111]，当位错接触到另一{112}滑移面时，发生交滑移，从而留下一段孪晶。图8所示为图6变形过程中d点的变形孪晶原子结构图。由图可知图7中的发生分解，形成了孪晶片段。由此判断孔洞在受到[100]方向极高应变率压缩时，通过位错和孪晶协同发生变形。

表3 R=12r孔洞模型在应变率108 s−1下压缩屈服点处不同滑移系的剪应力

*The star indicates that this system is active at yielding.

3 结论

1) 对单晶钨进行压缩变形，随孔径增大，孔洞处的应力集中增大，导致钨的压缩屈服强度降低，同时由于孔洞处断键数增加，导致材料的弹性模量减小。

2) 含有孔洞的单晶钨的屈服强度随应变率增加而增大，呈现出很强的应变率硬化行为，而弹性模量不随应变率变化而变化。

4) 在非晶化之前，孔洞的塑性变形是由位错滑移和孪晶变形的共同作用造成的。

[1] 王星, 李树奎, 王迎春, 等. 不同加载应变率下钨合金变形及破坏机理研究[J]. 北京理工大学学报, 2010, 30(11): 112−116. WANG Xing, LI Shukui, WANG Yingchun, et al. Study on deformation and failure mechanism of tungsten alloy under different loading strain rates[J]. Journal of Beijing Institute of Technology, 2010, 30(11): 112−116.

[2] 蔡国飙, 徐大军. 高超声速飞行器技术[M]. 北京: 科学出版社, 2012: 243−272. CAI Guobiao, XU Dajun. Hypersonic Vehicle Technology[M]. Beijing: Science Press, 2012: 243−272.

[3] 郭文启, 刘金旭, 吕翠翠, 等. 90W-7Ni-3Fe合金拉伸力学行为的应变率效应[J]. 稀有金属材料与工程, 2013, 42(4): 793−796. GUO Wenqi, LIU Jinxu, LÜ Cuicui, et al. Strain rate effect of tensile mechanical behavior of 90W-7Ni-3Fe alloy[J]. Rare Metal Materials and Engineering, 2013, 42(4): 793−796.

[4] MA Y, ZHANG J, LIU W, et al. Microstructure and dynamic mechanical properties of tungsten-based alloys in the form of extruded rods via microwave heating[J]. International Journal of Refractory Metals & Hard Materials, 2014, 42: 71−76.

[5] 刘海燕, 宋卫东, 宁建国. 不同晶粒度钨合金动态力学性能研究[J]. 材料工程, 2007(6): 4−7. LIU Haiyan, SONG Weidong, NING Jianguo. Research on dynamic mechanical properties of tungsten alloys with different grain sizes[J]. Materials Engineering, 2007(6): 4−7.

[6] REMINGTON T P, REMINGTON B A, HAHN E N, et al. Deformation and failure in extreme regimes by high-energy pulsed lasers: A review[J]. Materials Science & Engineering A, 2017, 688(Complete): 429−458.

[7] BOURNE N K. Atomistic views of deformation[J]. Nature, 2017, 550(7677): 461−463.

[8] MILATHIANAKI D, BOUTET S, WILLIAMS G J, et al. Femtosecond visualization of lattice dynamics in shock- compressed matter[J]. Science, 2013, 342(6155): 220−223.

[9] ZEPEDA-RUIZ L A, STUKOWSKI A, OPPELSTRUP T, et al. Probing the limits of metal plasticity with molecular dynamics simulations[J]. Nature, 2017, 550(7677): 492−495.

[10] WEHRENBERG C E, MCGONEGLE D, BOLME C, et al. In situ X-ray diffraction measurement of shock-wave-driven twinning and lattice dynamics[J]. Nature, 2017, 550(7677): 496−499.

[11] PLIMPTON S. Fast parallel algorithms for short-range molecular dynamics[J]. Journal of Computational Physics, 1995, 117(1): 1−19.

[12] ZHOU X, JOHNSON R, WADLEY H. Misfit-energy-increasing dislocations in vapor-deposited CoFe/NiFe multilayers[J]. Physical Review B, 2004,69(14): 144113.

[13] REN Q Q, FAN J L, GONG H R. Work function and cohesion properties of W-Fe interfaces[J]. Materials Letters, 2015, 145: 205−208.

[14] MI S T, GONG H R, FAN J L. Structural stability and mechanical property of Fe-W solid solutions from a constructed Fe-W potential[J]. Journal of Applied Physics, 2019,126(11): 115102.

[15] WEI W, CHEN L, GONG H, et al. Strain-stress relationship and dislocation evolution of W-Cu bilayers from a constructed n-body W-Cu potential[J]. Journal of Physics Condensed Matter, 2019, 31(30): 305002.

[16] STUKOWSKI A, ALBE K. Extracting dislocations and non-dislocation crystal defects from atomistic simulation data[J]. Modelling & Simulation in Materials Science & Engineering, 2010, 18(8): 2131−2145.

[17] JR W D C. Materials Science and Engineering: An Introduction [M]. United States of America: John Wiley & Sons, 1994: 150− 196.

[18] DUPONT V, GERMANN T C. Strain rate and orientation dependencies of the strength of single crystalline copper under compression[J]. Physical Review B Condensed Matter, 2012, 86(13): 71−75.

[19] TANG Y, BRINGA E M, REMINGTON B A, et al. Growth and collapse of nanovoids in tantalum monocrystals[J]. Acta Materialia, 2011, 59(4): 1354−1372.

[20] TANG Y, BRINGA E M, MEYERS M A. Ductile tensile failure in metals through initiation and growth of nanosized voids[J]. Acta Materialia, 2012, 60(12): 4856−4865.

[21] REMINGTON T P, RUESTES C J, BRINGA E M, et al. Plastic deformation in nanoindentation of tantalum: A new mechanism for prismatic loop formation[J]. Acta Materialia, 2014, 78: 378− 393.

[22] BRINGA E M, TRAIVIRATANA S, MEYERS M A. Void initiation in fcc metals: Effect of loading orientation and nanocrystalline effects[J]. Acta Materialia, 2010, 58(13): 4458− 4477.

[23] DUPONT V, GERMANN T C. Strain rate and orientation dependencies of the strength of single crystalline copper under compression[J]. Physical Review B, 2012, 86(13): 134111.

Molecular dynamics simulation of void evolution and its mechanical response in single-crystal tungsten under extreme strain rate

BAI Xiaodan, CHEN Xun, MA Yunzhu, LIU Wensheng, LIANG Chaoping

(National Key Laboratory of Science and Technology for National Defense on High–Strength Structural Materials, Central South University, Changsha 410083, China)

extreme high strain rate; molecular dynamics simulation; void; plastic deformation; dislocation

TG146.4

A

1673-0224(2020)04-288-08

国家自然科学基金青年科学基金项目(51801236)；国家自然科学基金重点项目(51931012)

2020−06−01；

2020−06−17

梁超平，副教授，博士。电话：13357312107；E-mail: cpliang@csu.edu.cn

(编辑 汤金芝)