基于周向SH0导波的管道轴向缺陷定量表征∗

贾九红 刘天阳 刘学成 廖作雨 张显程

(华东理工大学 承压系统与安全教育部重点实验室 上海 200237)

0 引言

管道在输送高温高压、强腐蚀和易燃易爆等流体方面起着重要作用。管道一旦发生泄漏或开裂，很容易导致爆炸事故，从而导致巨大的生命财产安全问题。因此，建立一种长期有效的在线监测方法，时刻掌握管道的缺陷损伤，具有重要意义。

相对于传统超声检测技术[1−3]，超声导波技术传播距离远、检测效率高、不容易漏检，受到了学者的广泛关注[4−5]。其中，水平剪切(Shear horizontal,SH)波在波导中的传播有许多优异的特性，对无损检测很有价值。研究表明[6−8]，在均匀介质的平板中，SH0模态沿振动方向的位移能量在厚度上均匀分布，且位移幅值较大，因此对板上下表面或者内部缺陷的检测具有相同的检测能力，且灵敏度较高。当前关于SH0导波的激励已经发展较为成熟，使用近似线源的反平面剪切可以在半无限空间中激励出SH波[9]，Jia 等[10]、Liao 等[11]使用压电晶片，在激励源满足理论值的条件下，激励出较为纯净的SH0波，并验证了其可靠性。

周向导波沿管道周向传播，因此对轴向缺陷敏感；相较于柱面导波，其检测距离相对较短，有利于验证环形焊缝等复杂条件或者管壁较厚的情况下缺陷是否存在；同时通过优化选取模态和频率提高识别精度，因此周向导波逐渐受到青睐。其中Grace等[12]、Viktorov[13]、何存富等[14−15]、黄松龄等[16]均对管道周向超声导波的传播特性进行了研究，发现曲率半径对频散特性存在影响；李隆涛等[17]、葛建明等[18]、张旭等[19]验证了周向导波对轴向缺陷检测的可行性；Luo 等[20]采用简化的二维单元模型研究了周向SH导波与轴向缺陷的相互作用关系，结果表明反射系数与轴向缺陷的深度和长度尺寸存在对应关系；张在东等[21−22]分别通过数值模拟和试验研究验证了周向SH波和周向Lamb波对厚壁管道外壁缺陷灵敏度较高；Wang等[23]使用开发的有限元程序包，通过结合周向SH导波的反射系数和透射系数，简单实现了轴向缺陷的定量检测。

SH0导波不易频散的特性以及其激励技术的日渐成熟，使此类检测方法受到学者们的关注，上述学者对周向导波的传播特性以及损伤检测进行了相应研究，但是对于利用SH0导波进行确定定量表征的研究相对缺乏，基于此的检测方法尚不成熟。本文以数值模拟和试验相结合的方式，以反射系数和透射系数为参数，建立量化模型表征轴向缺陷的深度和长度尺寸。

1 周向SH导波的传播特性

沿管道周向传播的超声导波称之为周向导波。其中周向SH导波在管道上位移振动方向沿轴向z，传播方向沿周向θ，如图1所示。本文采用Disperse软件绘制其频散曲线，设置壁厚为1 mm，材料为316L(参数如表1所示)。

图1 管道周向SH导波传播示意图Fig.1 Schematic diagram of pipe circumferential SH guided wave propagation

表1 316L 材料参数Table1 Material properties for 316L steel

管道周向导波的频散特性不仅与频厚积相关，也与管道曲面的曲率半径有关。提取不同曲率半径下的周向SH0模态的群速度频散曲线数据，探究曲率半径对周向SH0模态传播特性的影响，如图2所示。分析图像可知：在较低频率范围，周向SH0群速度随频率变化明显；频率较大时，群速度随频率变化较小；曲率半径越小，群速度随频率的变化量越大。因此在利用周向SH0导波对管道缺陷进行检测时，应关注其曲率半径，对群速度进行适当校准，可提高缺陷定位检测的精度。

对于周向SH0模态导波的波结构，已有学者做出相关研究[16]，无论曲率半径为何值，周向SH0模态的径向位移和周向位移均为0，因此周向SH0模态不存在离面位移，这种特性决定了周向SH0模态在传播过程中不易受管道外界液体或者包覆层的影响，相对于其他具有离面位移的导波，能量泄露较小、衰减小，有利于远距离传播。

图2 不同曲率半径下周向SH0模态的群速度Fig.2 Group velocities of circumferential SH0 modes with different bending coefficients

2 周向SH0导波和轴向缺陷定量表征的数值模拟

2.1 有限元模型的建立

考虑到实际缺陷具有三维特征，因此选用Solid164单元，建立壁厚1 mm、外径100 mm、轴向长为50 mm的直管段有限元模型，缺陷均设置为矩形槽，网格划分单元尺寸为0.2 mm。根据周向SH波的振动特点，模拟时在图3所示位置施加由汉宁窗调制的5周期轴向位移载荷作为激励源。模型中激励源、缺陷和透射信号接收点三者的相对位置如图3所示，分别相隔60◦，且都位于轴向正中间位置。激励源加载振动方向沿管道轴向。为了能够有效检测小尺寸的缺陷且只有单一的周向SH0模态，激发频率为1 MHz。

图3 管道截面示意图Fig.3 Pipe section diagram

2.2 周向SH导波与轴向缺陷尺寸定量关系数值模拟研究

在探究轴向缺陷长度作为单一变量与周向SH导波的作用关系时，固定其他参数不变，只改变轴向缺陷长度。缺陷的周向宽度取管道周长的1/360，约为0.87 mm(以弧度表示为π/180)，径向深度为0.6 mm，轴向长度从2 mm 逐渐增加到20 mm。在模拟过程中同样分别提取自激自收信号和一激一收信号，图4和图5分别列举了4 mm和16 mm 缺陷长度尺寸的反射信号和透射信号时域波形图。

在管道轴向缺陷深度和宽度恒定的情况下，轴向缺陷长度改变时，反射信号峰值有明显变化，即反射信号对轴向缺陷长度变化敏感；轴向长度改变较小时，透射信号能量变化不是很明显。为了更好地定量表征周向SH0模态与轴向缺陷尺寸的关系，引入反射系数R和透射系数T的概念，其表达式如下：

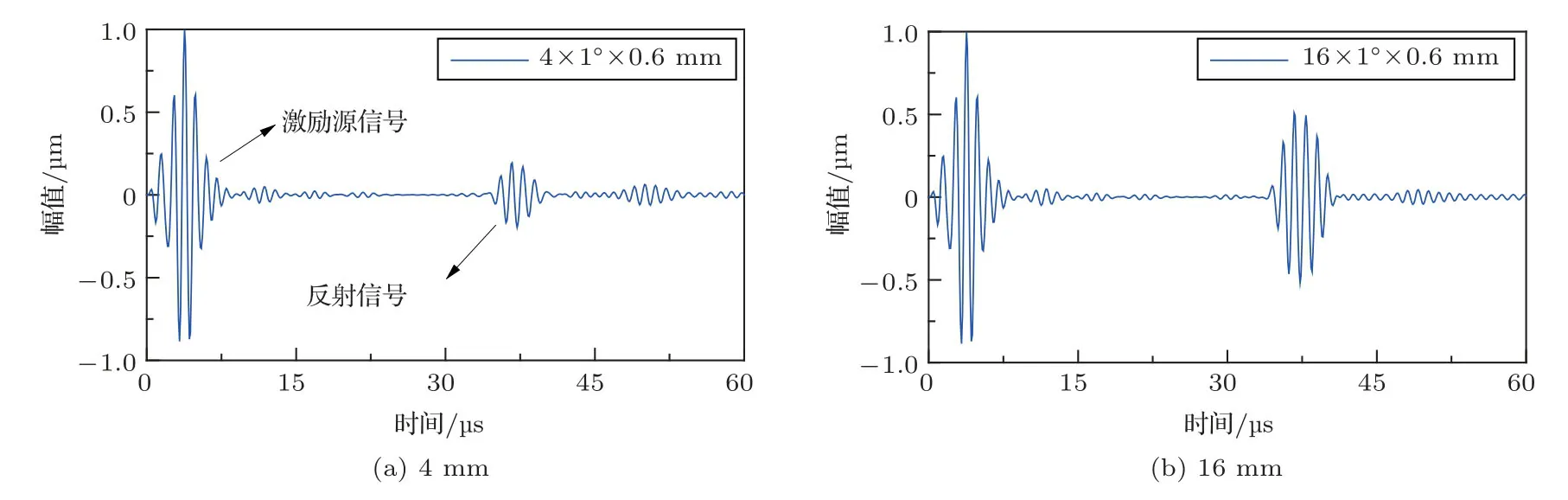
图4 不同缺陷长度的反射信号图Fig.4 Reflected signal diagrams of different defect lengths

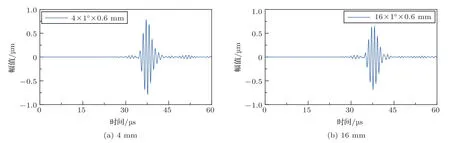
图5 不同缺陷长度的透射信号图Fig.5 Transmitted signal diagrams of different defect lengths

其中，A1为始波信号峰-峰值，AR为缺陷反射信号峰-峰值；A2为无缺陷时的透射信号峰-峰值，AT为有缺陷时的透射信号峰-峰值。分析表达式可知，在始波信号峰-峰值一定时，反射信号峰-峰值越大，则反射系数越大，这意味着导波经缺陷反射的信号能量越高；在无缺陷透射能量一定时，在含缺陷情况下透射能量越高，则透射系数越大，即代表着导波透过缺陷的信号能量越高，穿透能力越强。通过式(1)和式(2)将回波信号转换为反射系数、透射系数数值，便于定量分析。

使用相同的方法，保证缺陷的周向宽度为π/180，轴向长度为12 mm，缺陷深度分别为壁厚的20%、40%、60%、80%和100%(即贯穿缺陷)，提取模拟过程中自激自收信号和一激一收信号。

2.3 回波信号与轴向缺陷的定量分析

根据2.2节的模拟结果，增加有限元模型，完善周向SH导波与轴向缺陷尺寸的量化分析方法，继续丰富不同深度和长度下的反射系数和透射系数数据，提高准确性和可靠性。对模拟数据拟合可得周向SH导波反射系数和透射系数随轴向缺陷深度比和长度变化曲线，如图6和图7所示。

分析图6和图7可知：(1)无论何种深度比下，反射系数随轴向缺陷长度增大均先快速增大然后逐渐变缓，透射系数则呈现先迅速降低后缓慢降低的趋势；(2)同一长度下，深度比越大，反射系数相差越大；透射系数也相差越大。通过建立上述的反射系数和透射系数与轴向缺陷长度和深度比的拟合方程表，可以对该范围内直管中的轴向缺陷实现定量分析并预测。考虑到实际工程中需要综合考虑深度比和长度与反射系数和透射系数的关系，为此将缺陷长度和深度比作为横纵坐标，可得图8和图9所示云图。分析可知任意一个反射系数或者透射系数可以分别对应云图中的一条等值曲线，同时曲线上的任意一点的横纵坐标又分别对应相应的轴向缺陷长度和深度比。当反射系数所对应的轴向缺陷长度和缺陷深度比与透射系数所对应的长度和缺陷深度比最为接近时，即认为是缺陷的实际尺寸。运用此种超声导波幅值定量表征缺陷的方法，随着检验数据的增多，精确性和可靠性也会越来越高。

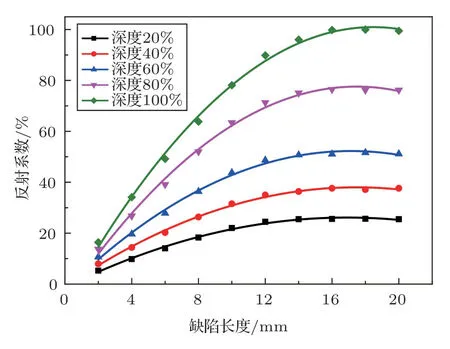
图6 反射系数模拟曲线Fig.6 Simulated curves of reflection coefficient

图7 透射系数模拟曲线Fig.7 Simulated curves of transmission coefficient

图8 反射系数云图Fig.8 Reflection coefficient contour

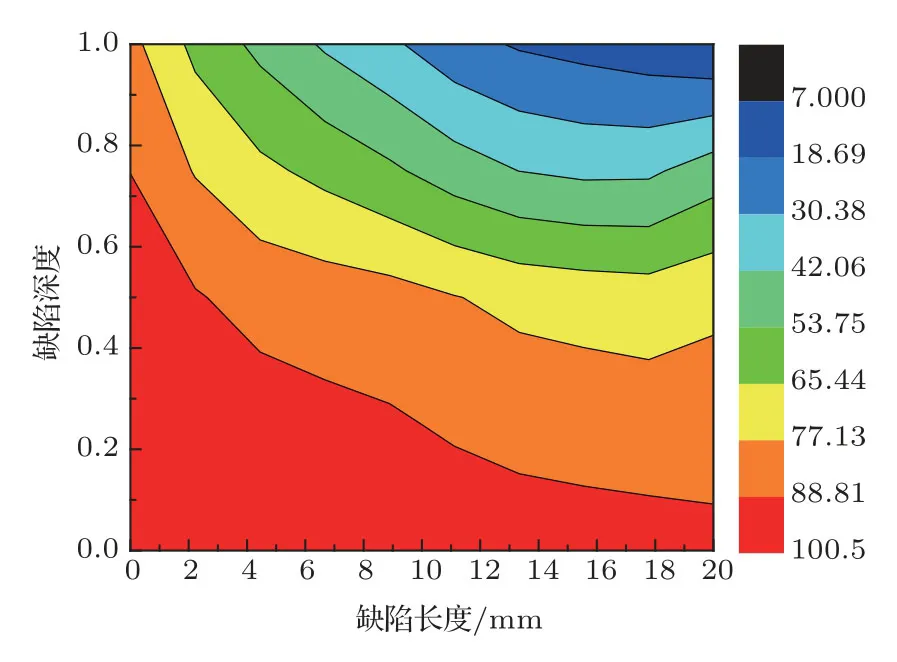
图9 透射系数云图Fig.9 Transmission coefficient contour

3 管道周向SH导波与轴向缺陷定量试验研究

3.1 试验系统的搭建

本试验主要是验证管中周向SH导波定量表征轴向缺陷的可行性。试验设备有超声信号发生器AFG3021C、信号放大器AG1006、双工器RDX-6、数字示波器MDO3012以及设备连接线、鱼夹线等。超声换能器使用PZT-5H的d35式厚度剪切压电晶片，尺寸为15 mm×1 mm×1 mm，频率1 MHz。晶片极化方向P及贴片如图3标记所示，长边沿管道轴向。压电晶片加载的振动方向沿管道轴向，与极化方向P相同，周向SH0波传播方向沿管道周向，即图3中C方向[24]。试验材料为壁厚1 mm、外径100 mm、轴向长为50 mm的316L 直管，结构尺寸和材料参数均与模拟保持一致。图10为自激自收试验连接图，可用于接收和提取自反射信号；图11为一激一收试验连接图，可用于接收和提取透射信号。缺陷位于正上方，压电晶片位于缺陷左右两侧相距缺陷60◦的位置。试验中采用5周期正弦脉冲信号，频率为1 MHz。

图10 自激自收试验示意图Fig.10 Diagram of the pulse echo mode

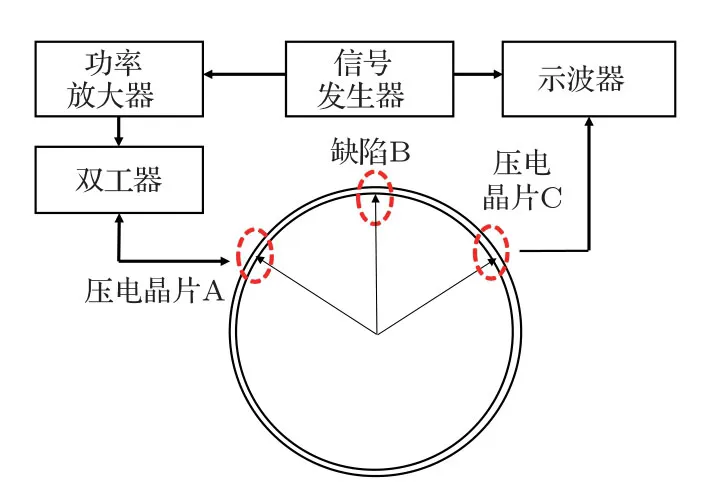
图11 一激一收试验示意图Fig.11 Diagram of the pitch-catch mode

3.2 周向SH导波与轴向缺陷长度定量关系试验

为了验证反射/透射系数与缺陷轴向长度之间的定量关系，加工一组周向宽度为π/180，径向深度1 mm(即贯穿)，轴向长度分别为4 mm、8 mm、12 mm、16 mm和20 mm的含缺陷管件。通过试验得到轴向缺陷不同长度的反射信号和透射信号。当缺陷的径向深度和周向宽度不变时，随轴向长度的增加反射信号的能量明显增加，透射信号的能量明显减少，即代表着反射信号和透射信号的能量幅值与缺陷长度存在对应关系。列举轴向长度4 mm和16 mm的波形图如图12和图13所示。

将不同缺陷尺寸下的反射/透射信号转化为对应的反射/透射系数，可得图14和图15。分析可知随着轴向缺陷长度的增加，反射系数先迅速增大，然后逐渐变缓。与模拟结果的比较，虽然实验数据略低于模拟值，但两者的总体变化趋势相似，且均呈现单调变化。透射系数随轴向缺陷长度增加呈现先快速下降，后缓慢减小的趋势。说明在缺陷长度较小时，反射系数和透射系数对缺陷长度的改变均更为敏感。其次，试验与模拟的匹配结果表明，透射系数匹配度优于反射系数。分析认为反射系数值与激励始波能量息息相关，由于试验过程中激励的始波信号经过压电晶片传递到被测试件中本身会有一个较大的衰减。因此，与理想的模拟条件相比，试验反射系数低于模拟反射系数。而透射系数是含缺陷试件的透射信号能量与无缺陷透射信号能量的比值，无需考虑激励始波进入被测试件的这一衰减过程。

图12 不同缺陷长度的反射信号图Fig.12 Reflected signal diagrams of different defect lengths

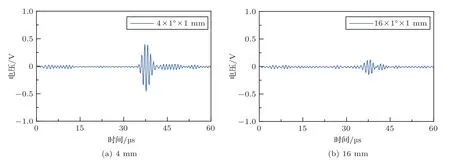
图13 不同缺陷长度的透射信号图Fig.13 Transmitted signal diagrams of different defect lengths

图14 反射系数模拟与实验值的比较Fig.14 Comparison of simulated and experimental reflection coefficients

图15 透射系数模拟与实验值的比较Fig.15 Comparison of simulated and experimental transmission coefficients

3.3 周向SH导波与轴向缺陷深度定量关系试验

为了验证反射/透射系数与缺陷径向深度之间的定量关系，加工一组周向宽度为π/180，轴向长度1 mm，轴向缺陷的深度分别为20%、40%、60%、80%和100%的含缺陷管件。通过试验得到轴向缺陷不同深度的导波反射信号和透射信号。当缺陷的轴向长度和周向宽度不变时，试验中轴向缺陷深度的增加使反射信号能量迅速增加，透射信号明显减小，即证明实际中反射信号和透射信号能量与轴向缺陷深度具有很强的相关性。

同样将不同缺陷尺寸下的反射/透射信号能量峰-峰值转化为对应的反射/透射系数，可得图16和图17。分析可知试验中周向SH导波的反射系数随着缺陷深度的增加而逐渐增大，且增速略有增大；而透射系数则逐渐减小，且减小速度越来越快。说明轴向缺陷深度越大时，反射系数和透射系数对缺陷深度的改变均越敏感。此外，在深度试验中，透射系数的匹配度明显降低。检查分析发现实际管道厚度略低于理论值，故加工固定深度缺陷后的剩余厚度小于理论值，从而导致透射系数减小。

图16 反射系数模拟与实验值的比较Fig.16 Comparison of simulated and experimental reflection coefficients

图17 透射系数模拟与实验值的比较Fig.17 Comparison of simulated and experimental transmission coefficient

4 结论

本文分析了周向SH0导波在管道中的群速度特性，周向SH0模态在截止频率以下群速度会随着频厚积变化而变化。但随着曲率半径的增大，群速度变化现象逐渐减弱；当曲率半径接近∞时，群速度几乎不变。通过模拟和试验分析周向SH0导波与不同尺寸的管道轴向缺陷的相互作用，验证了周向SH0导波对轴向缺陷定量表征的可行性。结果表明，对于轴向缺陷的长度，反射系数在初期快速增大，然后增速逐渐变缓；透射系数则呈现先迅速降低后缓慢降低的趋势。对于缺陷深度，反射系数随着深度的增加逐渐增大，且增速略有增大；透射系数则逐渐下降且下降速度越来越快。综上可知当缺陷长度较小、深度较大时，反射系数和透射系数对缺陷尺寸的变化更为敏感。