散流器送风口位置对排风柜性能的影响研究
2020-09-24张显相刘东
张显相 刘东
同济大学机械与能源工程学院
0 引言
近些年,随着全社会对公共卫生安全问题的重视,实验室及其安全成了人们关注的一个焦点。理化实验室主要是利用现代科学技术手段对物质的物理性能和化学成分进行检测分析的实验室,其安全性主要体现在实验室内部空气品质是否得到保证。试验中产生的一些挥发气体对人体有各种刺激作用,一些有毒有害物如笨、甲醛已被确定对人体有致癌性[1]。危险的工作环境对实验人员的生命健康造成巨大威胁。美国职业安全卫生管理局统计显示,实验室人员寿命比社会平均寿命少10 年[2]。排风柜是实验室内重要的局部通风设备,其提供一个封闭的通风操作空间,通过在内部形成负压,环境以捕集、排出烟气,颗粒等有害物质,从源头对污染物进行控制,保证实验人员安全。
实验室送风的作用时稀释室内污染物及维持相邻房间压力差,而送风口位置不当时,其会对排风柜形成不同程度的干扰,所以实验室送风应同时考虑其通风效率和对排风柜性能的影响,本文特别针对实验室常用的散流器送风口在不同布置位置的工况下对排风柜面风速,浓度的影响情况,来研究送风对排风柜性能的影响。
1 实验设施介绍
1.1 实验室介绍
同济大学排风柜全性能测试平台中,标准型排风柜背靠墙放置于封闭的实验室内,实验室尺寸(长×宽×高)为4 m×4 m×3.5 m(图1),本次实验所涉及风口为实验室唯一送风,排风依靠排风柜排风,实验室全面排风口关闭,房间微负压。
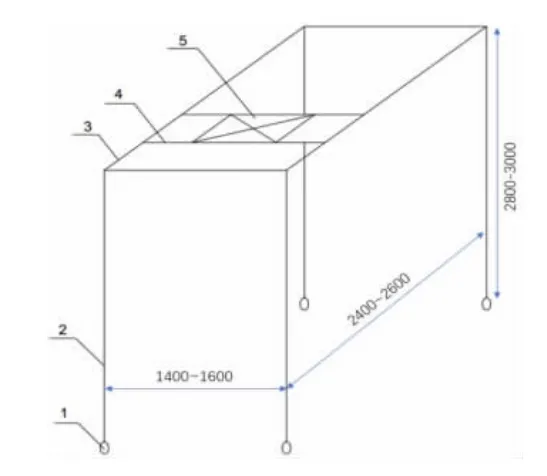
图2 风口支架示意图
图2 为风口支架示意图。图中,1 为移动轮(可滚动改变支架位置),2 为支柱,3 为滑轨,4 为支撑条(每个支撑条可在滑轨上单独滑动和固定),5 为风口(可固定在支撑条上)。
1.2 实验仪器介绍
采用Testo 425 高精度配合风速仪支架进行面风速测试,采用Thermo ScientificTMMIRAN SapphIRe 便携式环境空气分析仪实现一台仪器对多种气体的精确检测。
2 散流器不同位置对排风柜性能影响研究
2.1 散流器风口特征
在暖通设计领域,方形散流器具有良好的散流特性和美观的外形,结构形式多样,有1~4 个方向散流的形式,能满足不同类型天花板的要求,而且散流器内外框可以自由分离,拆装容易,便于调节风量,因此被广泛应用于空调通风系统的送风口[3]。其气流属于贴附(平送)型,多用于层高较矮、人员较密集的房间,可以作为送风口,一般情况下送风距离3~4 m 左右[4]。故很多带吊顶的实验室会选择散流器作为送风风口。本次实验选用的散流器面板由外边框和可拆卸风口内芯组成,固定式叶片用于水平送风,结合静压箱使用,效果良好,风口内芯可通过置于外边框内的弹簧装置定位或拆除。材质边框和内芯均采用铝合金6063-T5,表面用静电粉末喷涂。图3 为方散三视图,规格为525 mm(L)×525 mm(H),其中,X=672 mm,Y=522.8 mm。
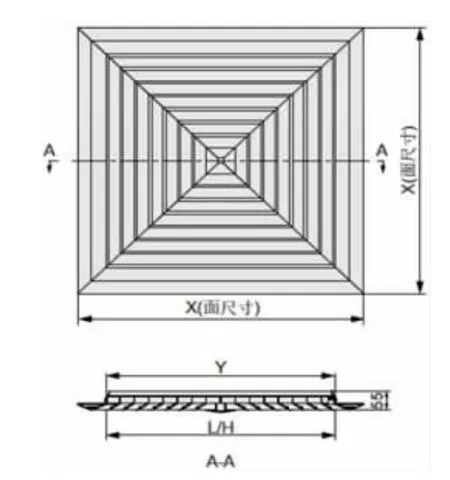
图3 方散三视图
2.2 正交试验
正交试验设计是研究多因素多水平问题的有效方法,它是根据正交性从全面试验中挑选出部分具有代表性的点进行实验,具有高效,快速和经济的特点,因而广泛应用于科学试验和生产实践中。
本文采用正交试验设计方法,通过极差分析和方差分析处理试验结果,得出最优解。
散流器风口对排风柜性能影响的研究中,各个因素及水平如表所示,三个因素分别为相对排风柜左右位置,相对排风柜前后位置,风口高度。每个因素设置三个水平,选用正交表L9(34),各因素相对位置描述。
因素A:相对排风柜左右位置,如图4 所示:
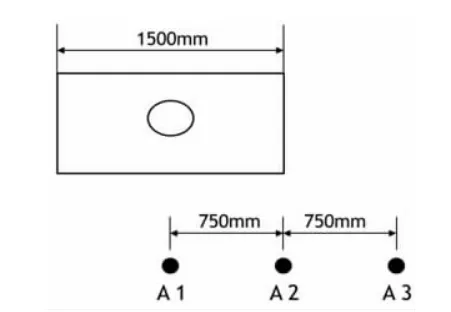
图4 相对排风柜的左右位置
因素B:相对排风柜前后位置,如图5 所示:
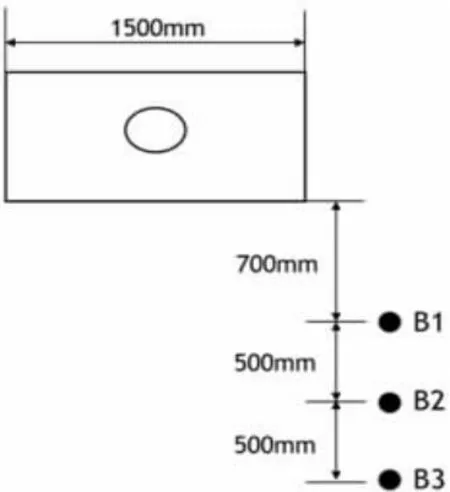
图5 相对排风柜的前后位置
因素C:风口的高低位置,如图6 所示:
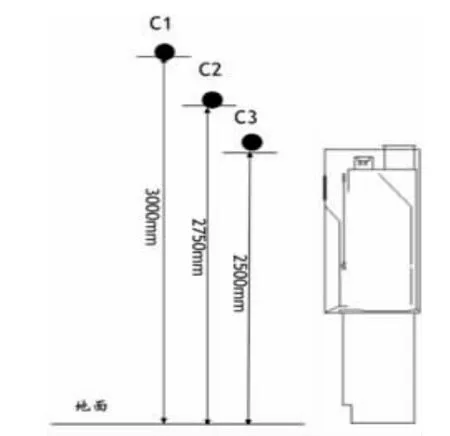
图6 风口高低位置
表1 为正交试验表。
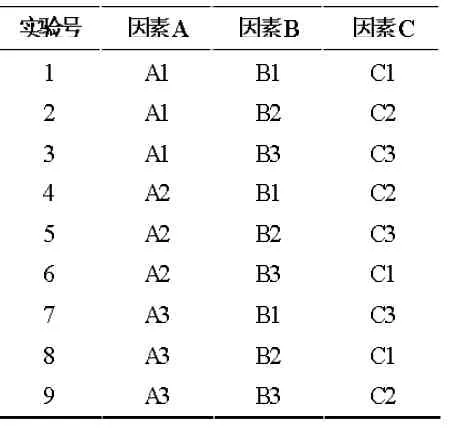
表1 正交试验表
2.3 结果分析(确定最佳的安装距离和安装高度)
对于排风柜的研究,面风速和控制浓度是排风柜的重要性能参数。对排风柜进行测试,排风柜静尺寸(长×宽×高)为1250 mm×860 mm×2200 mm,排风口为300 mm。拉门高度设在500 mm,排风量取整为1200 m3/h,送风量1100 m3/h。测试是在某实验室内进行,测试时实验门窗关闭。
2.3.1 面风速测定
面风速测试时,排风柜操作面均匀划分为12 个测点,测点布置如图7 所示:按照标准中的测试方法,使用风速温度测量仪测量各测点的风速。
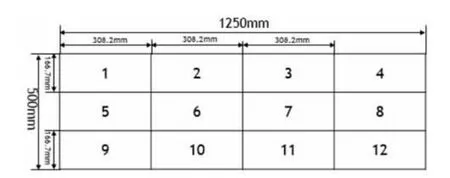
图7 面风速测试点位图
根据正交试验表所列的实验工况,保证送风、排风风量不变的情况下,调整散流器的位置测量不同工况下的面风速数据,通过分析各个测点20 组数据的标准差均值和各个测点20 组数据的均值的标准差反映不同工况下面风速的波动性和均匀性。
本文实验设计对每组实验的面风速进行测试,对排风柜操作面均匀划分为12 个测点,每个测点读取20 组数据,波动性分析先计算每个测点20 组数据的标准差,然后再对12 个测点的标准差数据求平均值,得出面风速标准差的均值,反映了面风速的波动性(表2)。
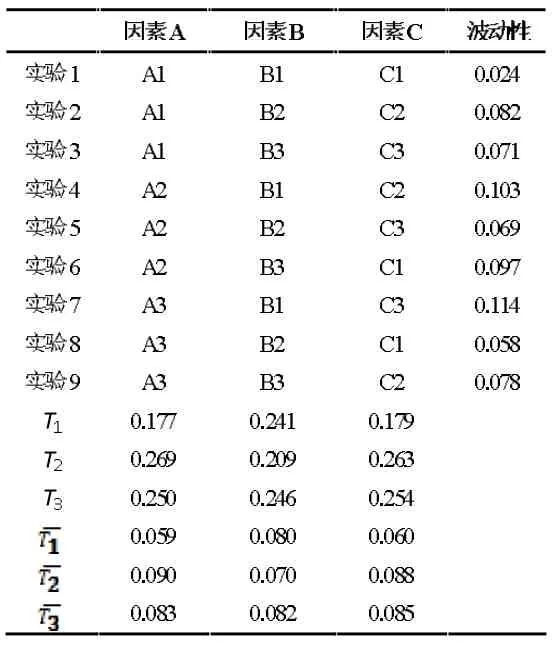
表2 面风速波动性
表2 中,T1,T2和T3这三行数据分别是各因素同一水平结果之和。例如,T1行A 因素列的数据0.177 是A 因素3 个1 水平的实验值的和,而A 因素3 个1 水平分别在第1、2、3 号实验,所以
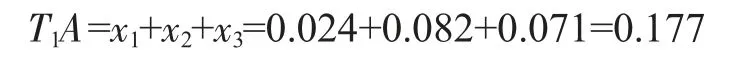
注意到,在上述计算中,B 因素的3 个水平各参加了一次计算,C 因素的3 个水平也各参加了一次计算。
其他的求和数据计算方式和上述方式相似,然后对T1,T2和T3这三行分别除以3 得到三行新的数据表示各因素在每一水平下的平均波动性。用各因素标准差均值的最小值的水平组合的方案,可以得出最优方案为A1B2C1。
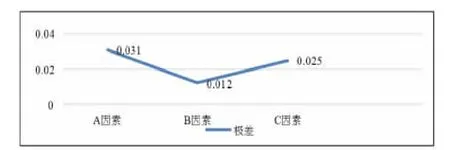
图8 各因素面风速波动性的影响
表3 反映面风速均匀性的测试和计算结果。通过对波动性的研究方法,可以得出面风速均匀性最好的方案为A3B3C3。
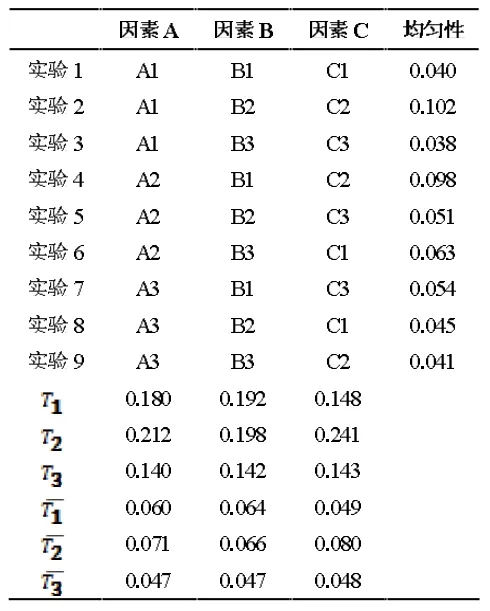
表3 面风速均匀性测试和计算结果
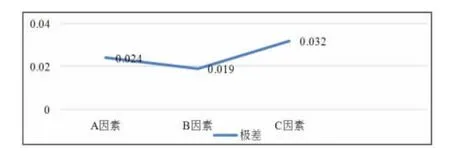
图9 各因素面风速均匀性的影响
2.3.2 浓度测定
在排风柜工作台面、内侧壁面上画平行于柜门的直线,在距柜门均为150 mm 的地方释放微量烟气。对于一个典型的带有垂直柜门的台式排风柜,需要三个位置:左、中、右。左边位置时,引射器的中心距离左侧壁300 mm。中间位置与左右两侧壁等距。右边位置距离右边侧壁300 mm。假人着实验室衣服,呼吸带距排风柜柜面垂直高度550 mm,距柜面水平距离75 mm(图10)。
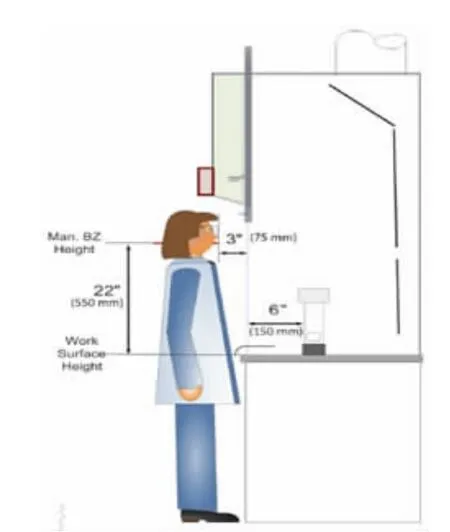
图10 假人位置
待房间背景浓度达到测试标准时,对每个工况每个位置下的污染物(假人吸入)浓度测试,每秒记录一次读数,共记录360 组数据。对各工况下数据进行分析,如表4 所示。
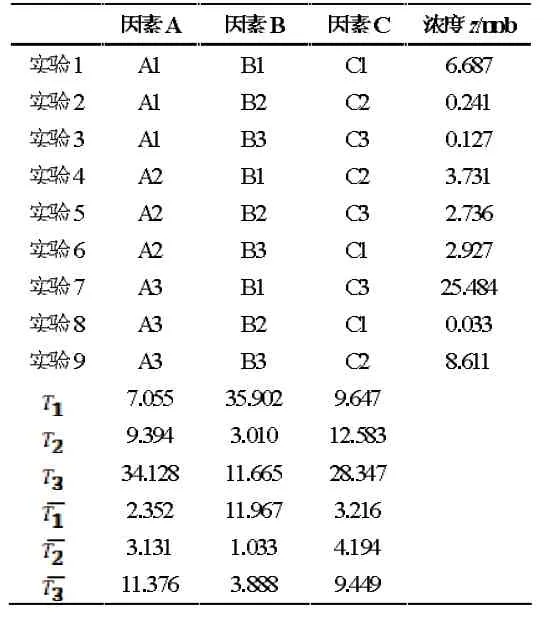
表4 浓度测试和计算结果
表4 中,T1,T2和T3这三行数据分别是各因素同一水平结果之和。例如,T1行A 因素列的数据7.055 是A 因素3 个1 水平的实验值的和,而A 因素3 个1 水平分别在第1、2、3 号实验,所以
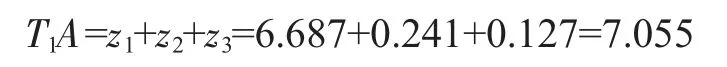
注意到,在上述计算中,B 因素的3 个水平各参加了一次计算,C 因素的3 个水平也各参加了一次计算。其他的求和数据计算方式和上述方式相似,然后对T1,T2和T3这三行分别除以3 得到三行新的数据和表示各因素在每一水平下的平均浓度。用各因素均值的最小值的水平组合的方案,可以得出最优方案为A1B2C1。
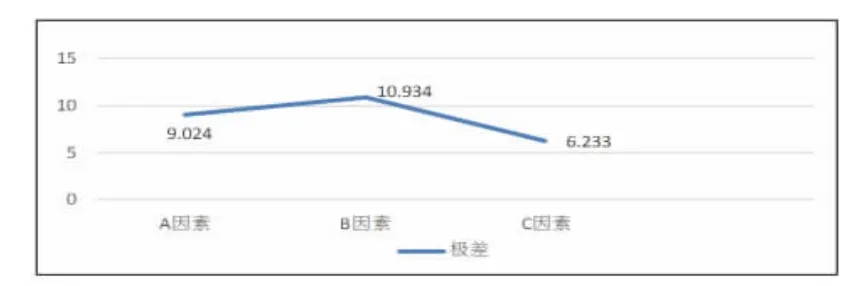
图11 各因素对浓度的影响
通过对浓度与面风速分析结果的对比分析,最优组合信息如表5 所示:
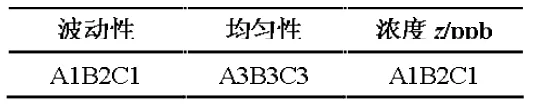
表5 面风速与浓度的对比
从表5 可得出如下结论:散流器风口工况下,风口的位置最优组合为A1B2C1,面风速的波动性与浓度相关性大。
3 结论
通过对面风速波动性的研究,可以得出最优方案为A1B2C1,比较极差得到,A 因素的极差RA=0.031最大,表明A 因素对波动性的影响程度最大。B 因素的极差RB=0.012 最小,说明B 因素对面风速波动性的影响程度不大。影响大小顺序依次是A>C>B。
同样对波动性的研究方法,可以得出面风速均匀性最好的方案为A3B3C3。影响大小顺序依次是C>A>B。
通过对浓度的分析,用各因素均值的最小值的水平组合的方案,可以得出最优方案为A1B2C1。比较极差得到C 因素的极差RC=6.233 最小,说明该风口的工况下C 因素对浓度的影响程度不大。影响大小顺序依次是B>A>C。
