竖直矩形小通道内上升流沸腾换热规律研究
2020-09-24黄雪松伍丹丹马雯
黄雪松 伍丹丹 马雯
中国石化中原油田分公司石油工程技术研究院防腐中心
0 引言
由于板翅式换热器结构紧凑,传热效率高,经济性好以及可同时进行多种介质换热等优点,在制冷,空调以及航空等领域得到广泛应用[1-2]。其主要由许多矩形流道构成[3-4],制冷剂在通道内部进行沸腾换热,其沸腾换热性能设计是一个技术难点问题。由于沸腾换热的多变性和复杂性国内外大量实验研究成果各不相同[5],目前对沸腾换热机理认识方面还存在分歧。如文献[6-7]研究表明由于对流沸腾换热机理作用沸腾换热系数随干度、质量流率增大而增大,而热流密度对沸腾换热系数影响较小。文献[8-9]表明由于核态沸腾和对流沸腾换热机理共同作用,沸腾换热系数随干度,热流密度以及质量流率增大而增大。同时,上述实验研究都提出了相应经验关联式,但这些关联式都是以有限实验数据为基础,将其应用于实际工程有待进一步验证[9]。
对于沸腾换热研究,数值模拟方法比实验方法具有更大的优越性[10-11]。所以很多学者采用数值模拟技术对沸腾换热机理进行模拟[12],如文献[13]采用CFX 对垂直套管内过冷沸腾换热进行模拟与试验对比,验证了上升汽液两相流沸腾传热模拟的可靠性。文献[14]以文献[15]管束外垂直试验台为原型,采用CFX 对管束外垂直上升汽液两相流沸腾传热特性进行模拟,得出不同入口温度、热流密度和质量流速下管束外狭窄通道内的热工水力特性。在上述汽液两相沸腾换热模拟中,沸腾换热过程均是通过汽液相间热质交换来实现,汽液相间热质交换率被认为与汽液相界面面密度Agl和汽液相间温差成比例[16-18]。在CFX 的Mixture 模型中,汽液相界面面密度是汽液相界面交互深度的函数,所以合理的汽液相界面交互深度是准确模拟沸腾过程的关键。在CFX 中并没有给出汽液相界面交互深度的具体确定方法,只是作为一个需要确定的参数给出,目前仅文献[19]提出了其确定方法。
本文对沸腾换热模拟中汽液相间热质交换原理进行分析,依据文献[19]方法计算汽液相界面交互深度,并借助CFX 软件对文献[1]实验工况进行模拟,并与实验数据进行对比分析。在保证模型准确性基础上,模拟分析了干度、质量流率对R21 在竖直矩形小通道内上升流沸腾换热的影响规律,并与文献已有经验关联式进行对比分析。
1 沸腾换热数值模拟模型分析
1.1 汽液相间热质交换模型
对于沸腾换热模拟,汽液两相之间热质传递通常采用汽液两相质量方程、能量方程的源项来实现。汽液相间质交换量是通过单位体积汽液相间质交换量模拟,其可表示为[18-19]:

式中:Γlg为单位体积内在单位时间从汽相进入液相的质量;Agl为汽液相界面面密度为单位汽液相界面的质量流率。
汽液相间显热换热量是通过单位体积汽液相间显热换热量模拟,其定义如下:
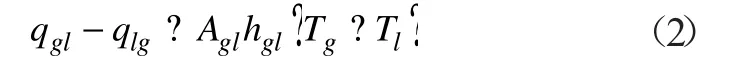
式中:qgl(qlg)为单位体积内在单位时间从液(汽)相进入汽(液)显热量;hgl为汽液相界面换热的对流换热系数;Tg为汽相温度;Tl为液相温度。
对于汽液相在相界面换热的对流换热系数hgl可以用汽液相间无量纲怒谢尔特数Nugl表示,即
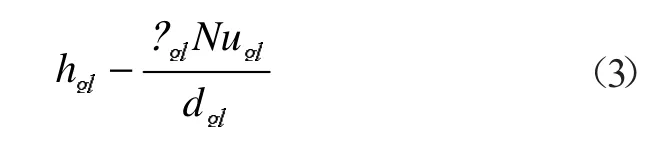
式中:λgl为汽液相综合导热系数;Nugl为汽液相界面怒谢尔数;dgl为汽液相界面交互深度。
依据式(1)和式(2)可以得出,要保证汽液相间热质交换模拟结果的准确性,需确定合理的汽液相界面面密度Agl、汽液相在相界面换热的对流换热系数hgl以及单位相界面质量流率在相间无量纲怒谢尔特数Nugl已知时,汽液相在相界面换热的对流换热系数hgl可按式(3)确定。
1.2 热相变模型
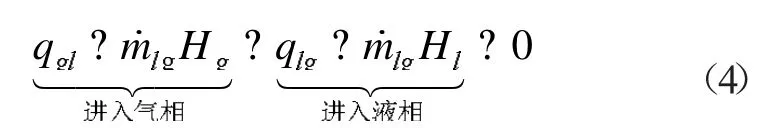
式中:Hg、Hl分别为汽、液相的焓值。在沸腾换热中上式可表示为
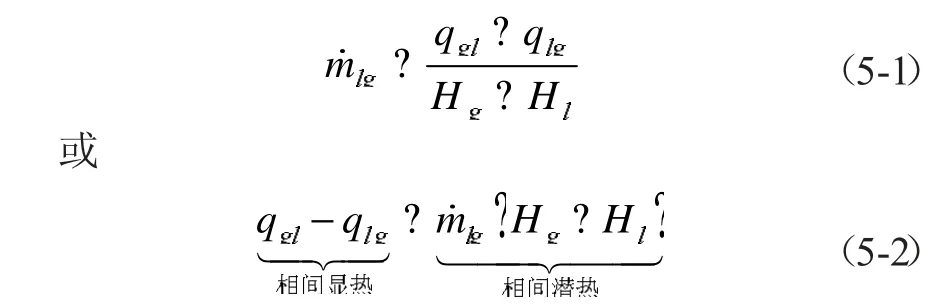
式(5)可得出汽液相间显热交换量等于相间质交换所需潜热量。
1.3 Mixture 模型中相界面面密度
对于式(1)和式(2)中汽液相界面面密度Agl,在CFX 的Mixture 模型中通过汽液相界面交互深度dgl进行计算。单位体积汽液相界面面密度定义如下:

式中:rg、rl分别为汽、液相体积分数。
式(6)表明汽液相界面面密度Agl与汽液相体积分数rg、rl以及汽液相界面交互深度dgl有关,合理确定汽液相界面面密度Agl的关键在于确定合理的汽液相界面交互深度dgl。目前,主要凭借实际工程经验确定汽液相界面交互深度dgl,仅文献[19]提出了一套理论方法对其进行预测,本文将采用该方法对汽液相界面交互深度进行预测。
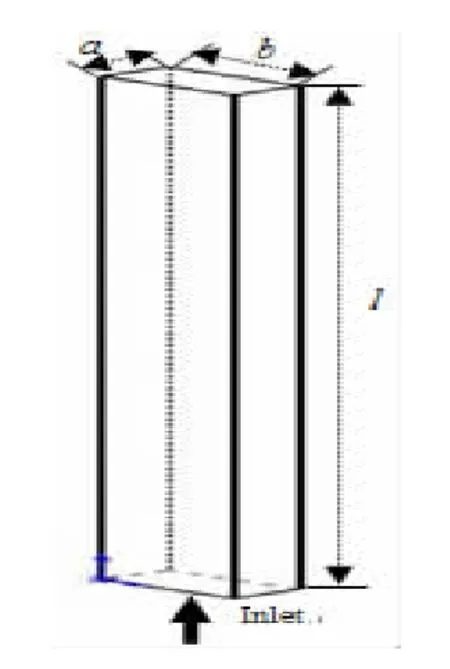
图1 竖直矩形流道
2 数值模拟模型建立
本文依据文献[1]实验模型建立了竖直矩形流道(1.6 mm×6.3 mm×290 mm)内沸腾换热模拟模型,借助ICEM 软件对模型进行了网格划分。为保证模拟结果的准确性,考虑壁面边界层对沸腾换热性能的影响,对壁面边界层进行网格加密。同时,为保证计算结果的准确性,提高计算效率,本文对模型进行网格无关性验证,并最终确定网格数为130 万,其模型见图1。同时,在本文模拟中,能量和动量方程均采用非均相模型,湍流采用均相k-ε 模型。为保证上述方程的封闭性,有必要附加相应的边界条件,因此本文在竖直矩形小通道入口附加质量流率、温度边界,壁面附加定壁面热流密度边界。在保证模型封闭性基础上,借助CFX 软件对其沸腾换热规律进行模拟。
3 模型验证及结果讨论
文献[19]给出了干度为0.5,入口质量流率为215 kg/(m2·s),不同壁面热流密度时,沸腾换热系模拟值与实验数据对比的结果,并没有给出不同干度时的对比结果。由于竖直矩形通道内沸腾换热性能受干度和入口质量流率的影响明显,因此有必要验证在不同干度和入口质量流率时,沸腾换热系数模拟结果与实验数据的吻合性,从而保证该模型在不同干度和入口质量流率条件下的准确性。
图2 是不同干度时,沸腾换热系数模拟结果与文献[1]实验数据的对比结果。其中,图2(a)是质量流率为215 kg/(m2·s)、热流密度为6 kW/m2,不同干度时,沸腾换热系数模拟值与实验数据对比结果,结果表明模拟结果与实验吻合较好,在干度小于0.7 时模拟结果偏小,干度大于0.7 时模拟结果偏大,但其误差在±15%以内。同时,结果还表明:由于强制对流沸腾换热机理增强,干度越大沸腾换热系数越大。图2(b)是质量流率50 kg/(m2·s)、热流密度1.1 kW/m2,不同干度时,沸腾换热系数模拟结果与文献[1]实验数据对比结果。结果表明,模拟结果与文献[1]实验吻合较好,偏差同样在±15%以内,说明文献[19]中的汽液相界面交互深度确定方法在小流量、低热流工况时同样能准确预测沸腾换热规律。
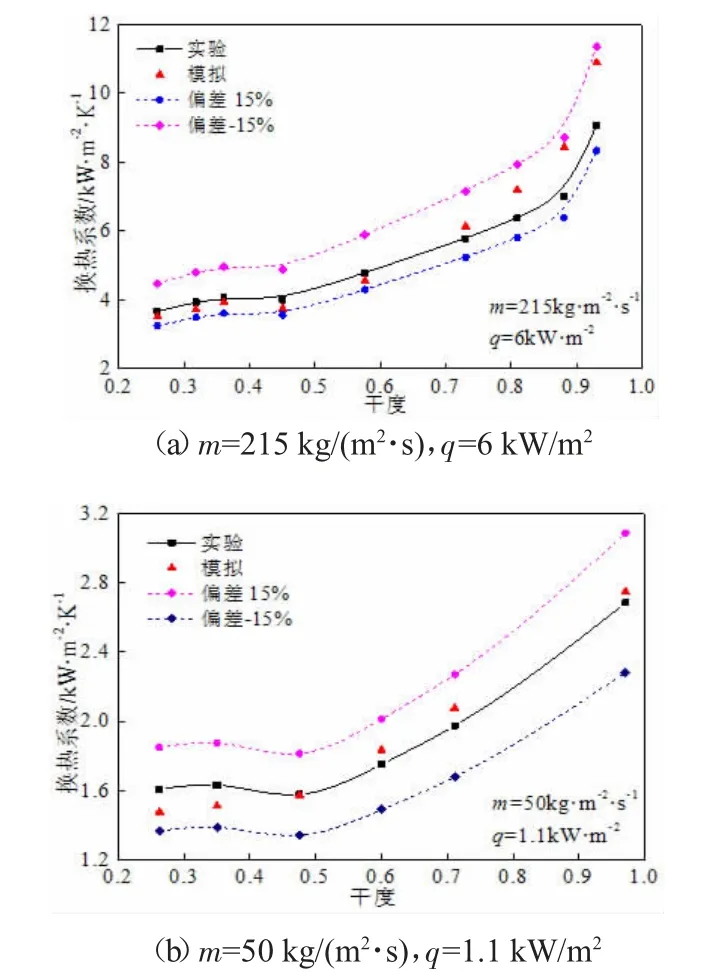
图2 不同干度条件下模拟结果与实验数据对比结果
在上述模型验证基础上,本节分析了不同干度、质量流率对沸腾换热的影响规律,并与文献[20-22]经验关联式(见表1)进行对比。图3 是质量流率215 kg/(m2·s)、热流密度6 kW/m2时,沸腾换热系数模拟值与文献[20-22]关联式计算结果对比。结果表明,在干度小于0.7 时,模拟与Warrier 关联式计算结果吻合较好,其偏差在15%以内。当干度大于0.7 时,模拟值大于关联式计算值,干度越大偏差越大。干度越大,沸腾换热系数越大,并且换热系数的增幅越大。图4 和图5 分别是壁面热流密度为6.0 kW/m2、入口质量流率为215 kg/(m2·s),不同干度时,距入口50 mm 断面的液相和汽相速度分布。结果表明,随着干度增大,矩形小通道内汽液相流速逐渐增大,从而使强制对流换热随干度增大而增强。综上所述,在竖直矩形小通道内,干度的增大将导致其内部汽液相速度增加,使矩形通道内强制对流沸腾换热机理增强,从而使沸腾换热系数随干度的增大而增大。
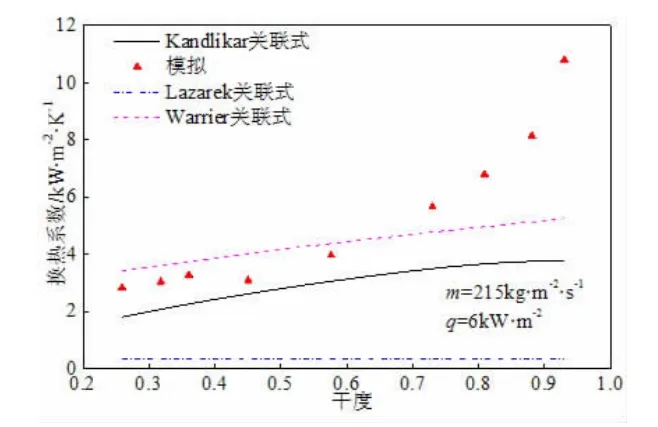
图3 干度对换热影响

表1 常用流动沸腾换热关联式
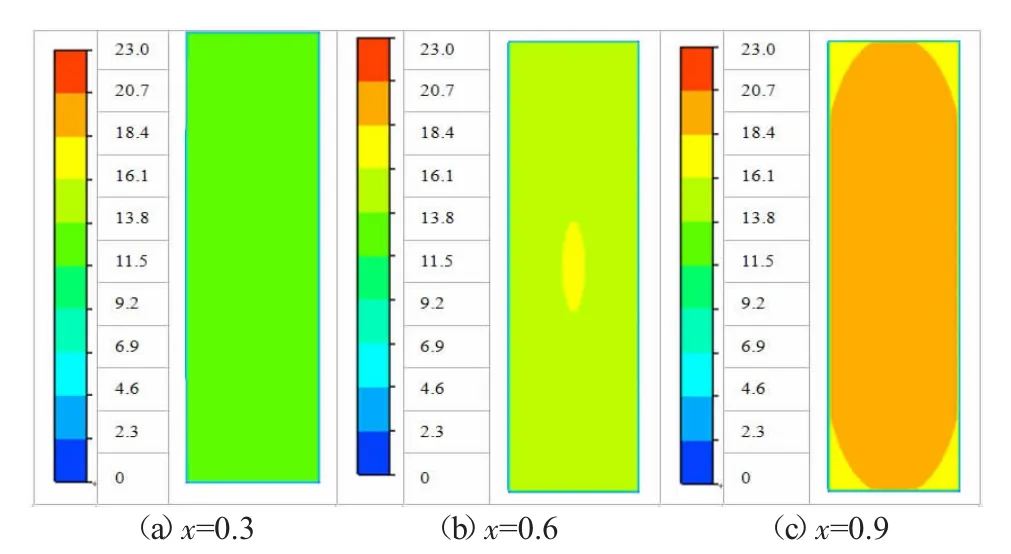
图4 液相速度分布图(m/s)
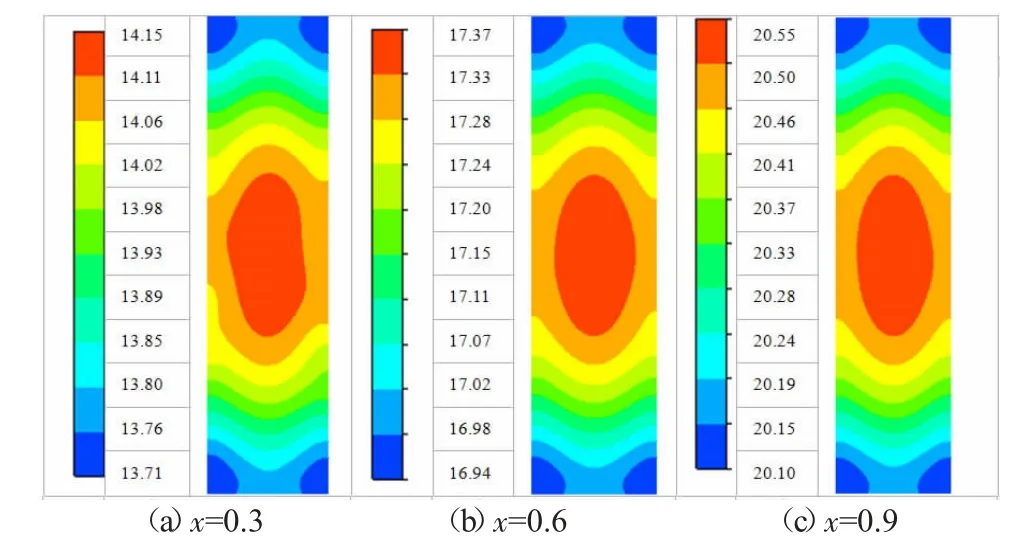
图5 汽相速度分布图(m/s)
图6 是不同质量流率时,沸腾换热系数模拟值与关联式计算结果对比。图6(a)是干度0.6、热流密度6 kW/m2,不同质量流率时模拟值与关联式计算结果的对比。结果表明,沸腾换热系数模拟值与Warrier 关联式计算结果吻合度较高,与Lazarek 关联式计算结果偏差较大。图6(b)是干度0.9、热流密度6 kW/m2,不同质量流率时模拟值与关联式计算结果的对比。结果表明,在干度0.9 时模拟结果偏大于关联式计算结果,质量流率越大则偏差越大,与图3 的结论具有一致性。文献[19]是以非共沸混合冷剂为工质对沸腾换热进行模拟,并与关联式进行对比,由于在不同干度条件下,非共沸混合冷剂汽、液相中各组分的含量将有所不同,从而导致其物性发生了很大的变化,因此上述结论与文献[19]所得结论偏差较大是合理的。图6 模拟结果还表明,沸腾换热系数随入口质量流率的增加而增大。为进一步分析入口质量流率对沸腾换热性能的影响规律,本文又给出了不同入口质量流率时,距入口50 mm 断面的汽相速度分布。图7 是干度0.6、热流密度6 kW/m2,不同入口质量流率时,距入口50 mm 断面的汽相速度分布。结果同样表明,随着质量流率增加矩形小通道内汽相流速逐渐增大。汽液相流速的增大会导致矩形小通道内冷剂强制对流沸腾换热机理的增强,因此沸腾换热系数随入口质量流率的增加而增大,本质上是由于对流沸腾换热机理随质量流率增大而增强所致。
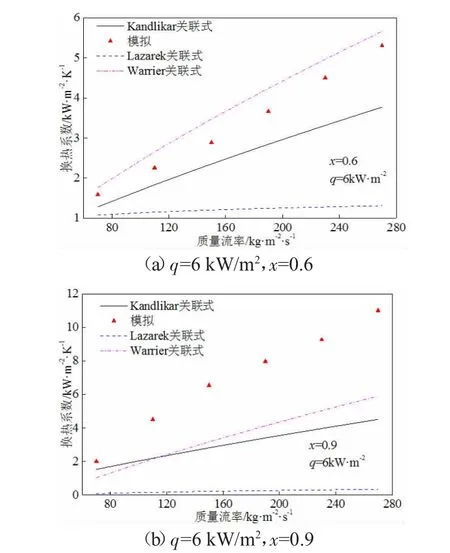
图6 质量流率对沸腾换热系数的影响规律
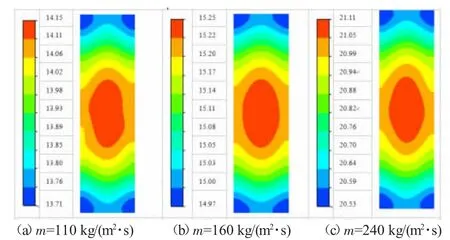
图7 汽相速度分布图(m/s)
4 结论
本文借助文献[19]汽液相界面交互深度确定方法,对R21 在竖直矩形小通道内上升流沸腾换热规律进行模拟。通过模拟与文献已有经验关联式计算结果对比分析,推荐了已有关联式,并提出了其使用范围。通过上述研究可得出如下结论:
1)模拟与实验对比分析结果表明,文献[19]汽液相界面交互深度确定方法,应用于不同干度和质量流率条件下的沸腾换热模拟仍具有很高准确性,其偏差在±15%以内。
2)干度、质量流率对沸腾换热性能的影响比较明显,并且随干度、质量流率的增大,强制对流沸腾换热机理有所增强,从而导致沸腾换热系数随干度、质量流率的增大而增大。
3)在干度小于0.7 时,模拟与Warrier 关联式计算结果吻合较好。在干度大于0.7 时,模拟与关联式计算结果偏差较大,干度越大偏差越大。
