奇异值与特征值扰动界估计

燕岩军，宋儒瑛，杨 帆

(1.山西机电职业技术学院 基础部，山西 长治 046011；

2.太原师范学院 数学系，太原 030619；

3.佳木斯大学 理学院，黑龙江 佳木斯 154002)

在科学和工程领域，矩阵研究应用广泛，并且许多问题可归结为矩阵特征值和奇异值相关问题.因此，对矩阵特征值和奇异值相关研究具有重要意义.近年来，矩阵特征值、奇异值研究越来越受到广泛学者的关注,并得出许多较好结果，主要涉及非奇异终端[1]、特征多项式[2]、特征值扰动[3]、奇异值扰动[4]、矩阵空间[5]等相关方面的研究.特别地，Eisenstat[6]与Ipsen等[7]对于可对角化矩阵给出乘法扰动下特征值扰动结果：

(1)

这里κ(X)=‖X‖2‖X-1‖2.

随着对矩阵特征值、奇异值问题深入研究，许多学者在研究方法上也不断探索创新，这些方法对研究矩阵特征值、奇异值在误差精确性方面起着非常重要的作用，如矩阵迭代判定法[8]、正交矩阵对角化法[9]、正规矩阵对角化法[10]等.本文在这些方法研究基础上，对矩阵特征值、奇异值问题作进一步研究.通过构造双随机矩阵、结合矩阵相关技巧运算，给出一种新的证明方法，并得出新结论：

(2)

最后，通过比较式(1)与式(2)结果，可以知道式(2)结果更优，说明本文结论改进推广了Eisenstat与Ipsen等人已有结果，具有一定的研究意义.

首先对文中字母符号进行简要说明.在文中使用符号Cm×n来表示m×n阶复元素矩阵的全体，用符号I代表单位矩阵，用符号A*表示矩阵A的共轭转置，用符号eig(A)表示方阵A的全体特征值，用符号‖·‖2表示矩阵的谱范数，用符号‖·‖F表示矩阵的F范数.

1 预备知识

定义1[11]假定矩阵A∈Cn×n.若存在一个n×n阶可逆矩阵Q，并且满足A=QΛQ-1，那么就称矩阵A是一个可对角化矩阵.其中这里Λ=diag(λ1,λ2,…,λn)为对角矩阵，并且λi(i=1,2,…,n)表示矩阵A的特征值.

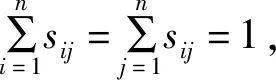
说明对于任意一个n×n阶方阵B，结合矩阵奇异值知识可以将其分解为B=U*∑V.其中这里的U、V表示酉矩阵，∑=diag(σ1,…，σn)，σi表示方阵B的奇异值，并且有σ1≥σ2≥…≥σn≥0.

2 主要结论

引理1[12]假定矩阵S=(sij)是一个n×n阶的双随机矩阵.对于任意一n×n阶方阵T=(tij)，那么则存在{1,2,…,n}中的一个排列τ，使其满足：

(3)

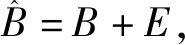
(4)

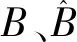
根据矩阵B奇异值分解，可知：

B-1=(U∑V*)-1=(V*)-1∑-1U-1=V∑-1U*.

(5)

因此，结合矩阵B奇异值分解可以得出:

(6)

同理：

(7)

(8)

这里用符号Re(α)表示复数α的实部.

这样，将引理1结果应用到式(8)中，可以知道存在{1,2,…,n}的一个排列τ，满足式(9)：

(9)

根据式(9)可知定理成立.证毕

特别说明：对于非奇异矩阵奇异值相对扰动研究，本文通过构造双随机矩阵法并结合Li R C[13]一文相应技术手段，给出矩阵加法扰动下非奇异矩阵奇异值相对扰动上界的一个新结论，具有一定的推广意义.这是因为，对于n×n阶非奇异矩阵B，Demmel与Veselic[14]证明得出：

(10)

尽管Demmel和Veselic得出奇异值相对扰动上界比较好，但Li R C[15]一文中通过进一步研究证明并得出：

(11)

这说明，Demmel和Veselic得到的结果中奇异值相对扰动界的和并不是最小.由此可见，本文结论具有一定的研究价值.如果在本文基础上还能进一步找到比本结论还小的上界，这对研究矩阵奇异值相对扰动意义重大，这是以后努力的方向.

其中这里的λi(i=1,2,…,n)表示矩阵A的特征值.

(12)

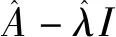
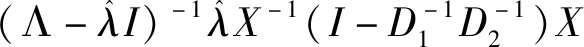
(13)

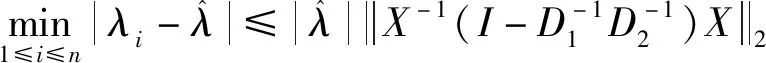
3 结论

对于可对角化矩阵，给出矩阵乘法扰动下特征值差的扰动上界估计，并且本文得到定理2上界估计更优，改进了Eisenstat、Ipsen等的结果。

这里因为,比较式(1)与式(2)，根据矩阵谱范数定义，显然有：

(14)

由式(14)可以看出，本文定理2中得到的扰动上界比Eisenstat、Ipsen等得出的上界估计要小，所以本文定理2结论改进了参考文献[6,(定理6.1)]与[7,(定理5.1)]中的结论，具有一定的研究意义.