带线性项和积分型系数问题的解
2020-09-24周荧,王跃
周 荧,王 跃
(贵州大学 数学与统计学院,贵阳 550025)
众所周知,解决微分问题最终都转化为求微分方程,然而在物理、工程技术等方面出现的大量微分方程因为复杂而难以求出解析解,甚至在能求出解析解的情况下,也可能会因为表达式的繁杂而失去实用价值,从而技术员常常希望有简单的解析解,近似度非常高的简单表达式也可以,这样不仅有利于作数值计算,还方便作定性分析.如果一个表达式几乎处处满足微分方程及所要求的附加条件,而在那些不满足的地方可以忽略不计,那么这个表达式也叫近似解.由于求近似解的各种方法已经比较成熟[1],因此在很多文献中也常常只讨论微分问题解的存在与否、是否多解等基础理论.多年以来,在不同边界条件下问题:
(1)
解的研究仍是热点,因为它与梁振动模型[2]有关.而实际上它来源于经典的基尔霍夫振动模型:
(2)
其中ρ、h、p0、E、L均为常数,0 (3) 至少存在1个正解和1个负解,并利用反证法获得不存在正解的条件,但解的形式也没提到. 受文献[3,5,15-16]的启发,本文也考虑问题(3),不同于文献[11]的是a,b,为任意实数(常数参数均可),ΩRN(N≥1),将通过函数构造给出问题(3)的无穷多近似解和古典解,直观上可看出有正解、负解和变号解.另外,本文将详细说明问题(3)当ΩRN(N≥1)是划去坐标平面且无边界条件限制时也有无穷多古典解,而Ω含坐标平面中的点或是闭集时可以将之视为近似解. 关于负模量问题(1)解的存在性研究状况目前不多,除了前述文献之外,文献[18]推广了文献[9]的结果到全空间,文献[19]拓展文献[8]的问题到球上获得正解的存在唯一性,文献[20]推广文献[8]的结果到次线性指数,文献[21-23]的研究与文献[9,18]类似,文献[24]带有指数型非局部系数,文献[25]利用代数的方法获得1个2个或3个解的存在唯一性,文献[26]则推广负模量问题到变指数的情形并获得无穷多弱解. 定理1 设Ω⊆RN,如果=0,则问题(3)有无穷多近似解具有多项式型. 证明不失一般性,以R为例,可以任取其中的一个有界区间[c,d]⊆Ω,对过端点的由有限条折线组成的任意连续函数v(x),令: 那么u(x)|x∈(c,d)=0.注意到在(c,d)内,除了有限个不可导点外,u(x)是分段常数,因此几乎处处有u(x)=0并且有界,所以几乎处处满足v=0,从而根据v(x)的任意性可得出问题(3)有无穷多多项式型的近似解. 例1 当Ω=(c,d),=0时,是问题(3)的近似解. 定理2 设=0且ab>0,则当Ω⊂R时问题(3)有无穷多多项式型的古典解. 证明设ab>0,[c,d]⊂Ω是有界区间,取正整数m,n≥3,令: 例2 若满足Ω=(c,d),=0,ab>0,求证是问题(3)的古典解. 证明在Ω上u(c)=u(d)=0显然成立.而在Ω上,直接计算可得: 综上可知,u(x)是问题(3)的一对古典解. 推论1 设Ω=(c,d),=0且ab>0,则对所有过点(c,0)和(d,0)的二阶光滑函数v(x)而言,只要令则u(x)都是问题(3)的古典解,而此时古典解有无穷多个. (4) (5) 下面就a、b、满足不同情形时,对问题(3)的一些近似解和古典解的情况作介绍. 定理3 设b=0,a>0,Ω=R,则问题(3)有无穷多三角函数型的近似解. 证明若b=0,只要a>0,则对任意常数及整数m,-av=v有无穷多古典解: (6) 下面的定理主要讨论b≠0的情形,此时考虑关于的方程式可得: (7) 定理5 设a=0,b<0,Ω=(c,d),则问题(3)有无穷多三角函数型的古典解. 证明如果a=0,b<0,则问题(3)退化到特征值问题由于此时从而在零边值时它存在无穷多古典解: (8) 定理6 设=0,ab>0,Ω=(c,d),则问题(3)有无穷多三角函数型的古典解. 证明如果=0,ab>0,则此时问题(3)有无穷多古典解可表示为: 定理7 设Ω=(c,d),a,b,同为正或同为负,则问题(3)有无穷多三角型函数的古典解. 证明当a,b,同为正或同为负时,只要取正整数M使得则对所有n,m∈Z,只要|n|>M,问题(3)都有如下的古典解: (9) 定理9 设ab<0,Ω=(c,d),则在与之间时问题(3)至少有i个线性无关的三角函数型古典解. 证明如果ab<0,不难发现只要满足: 本部分可作为问题(3)的拓展,但非问题(3)当a,b,满足其他情形时的补充,因为这里Ω可以无光滑边界,也不要求连通.假设N是正整数,x∈RN|xi≠0,i=1,2,…,N,即是RN中划去坐标平面的集合,显然RN不是连通区域但却由2N个连通区域组成.设开集Ω考虑如下问题: (10) 这里a,b,为任意实数,可以是常数也可以是参数. 定理10 设Ω若ab>0或b>0,则问题(10)有无穷多古典解. 证明对N≥1,任取β>1,i>0(i=1,2,…,N).取则: 可得出: 因此当a,b,同为正或负时取β>1即可;ab>0时可取>0时,如果a=0则取β>1,a≠0可取 当满足ab>0或b>0时有一类古典解具有如下解析式: (11) 是问题(10)当满足ab>0或b>0时的近似解、特别当Ω=RN时,可以把式(11)看作是近似解. 本文使用构造函数的方法,构造出无穷多近似解和古典解满足所给的边值问题,然而利用变分方法只能得到对应泛函存在临界点,从而证明问题存在弱解,而给不出解的形式.对问题(3)而言,当=0时,定理1讨论u(x)=0几乎处处成立且有界,定理2和定理6围绕且u有界展开;当≠0时,定理4、定理5及定理7至定理9主要阐明-1>0的情形,定理8补充了文献[11]的N≥3到N=1,2;实际上,文中获得的近似解,在不可导处的单向极限导数存在并且有界而导致了这些不可导点在函数和非局部积分中总可以视其测度为零,因此这些不可导点是可以忽略的.另外还可以发现这些近似解几乎处处二次光滑.这种方法的优点是给出了近似解和古典解的很多形式,获得的结果是变分方法不可能完全达到的.利用类似的方式,联合特征值问题的谱理论,可以证明本文的结论对N≥2以及Neumann型零边值条件同样成立.根据算子方程的谱理论,本文的所有结果均可以推广到Ω⊂RN.1 零右端的多项式型近似解和古典解

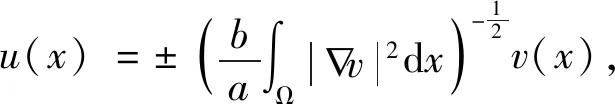

2 零边值的三角函数型近似解和古典解
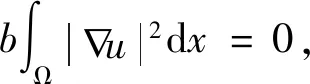
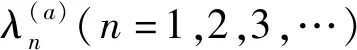
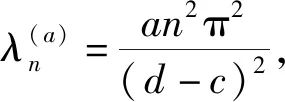




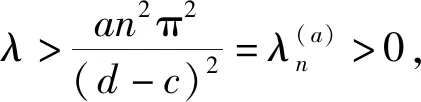

3 无边界的指数函数型解

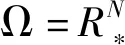
4 结语
