桥上CRTSⅡ型板式无砟轨道层间关键构件的地震响应规律及参数影响分析

冯玉林,蒋丽忠,周旺保,何彬彬,聂磊鑫,谭志化

(1.中南大学土木工程学院,长沙 410075； 2.中南大学高速铁路建造技术国家工程实验室,长沙 410075；3.华东交通大学土木建筑学院,南昌 330013； 4.中国科学院大学,北京 100049)

引言

CRTSⅡ型板式无砟轨道是中国特有的轨道结构形式之一，大量的应用在已建高速铁路线路中。该轨道结构放弃了长桥上无砟轨道必须设置断缝并在梁端处断开的原则，认为底座板是主要受力构件，各项设计均以底座板为核心开展。检算荷载主要为二期恒载、基础沉降、墩柱扭转、活载、制动/牵引、温差、收缩和徐变等，而地震荷载并未检算。由于我国地处欧亚与环太平洋地震带，是地震发生最为活跃的国家之一，因此，明确轨道结构中各关键构件的地震响应及损伤规律，是高速列车-桥梁-轨道耦合系统震后维修与运营的基础[1-3]。

目前，基于理论与计算机仿真的轨道结构地震响应已有大量研究：王炎等[4]、张永亮等[5-6]分别以某高速铁路连续梁桥与简支梁桥为研究对象，建立了考虑轨道约束及摩擦效应的“线桥一体化模型”，对延性与减隔震体系进行非线性地震响应分析，得出了轨道体系纵向刚度约束效应对桥梁下部结构地震反应的影响的结论。基于缩尺模型振动台试验的轨道结构的地震作用研究：Toyooka等[7]、Iemura等[8]、Petrangeli等[9]、Fitzwilliam等[10]、Kim等[11]进行了铁路桥梁的缩尺模型振动台试验以及理论分析，并建立了“线桥一体化模型”，研究了轨道结构对桥梁结构抗震性能的影响，讨论了轨道结构和桥梁结构在地震作用下的相互作用机理。高速铁路桥梁无砟轨道系统的地震损伤的研究：Tecchio等[12]针对欧洲铁路中占比较大的石拱桥，提出了完整的桥梁-轨道系统地震易损性分析流程。Park等[13-14]基于响应面法提出了用于桥梁-轨道系统地震损伤的评估方法，可以有效地估计任意的桥梁-轨道系统的地震易损性[15-16]。

通常，高速铁路桥梁结构地震损伤主要关注基础、墩柱和支座，但轨道结构亦会发生破坏。目前对轨道结构地震损伤研究已取得较多成果，但大多研究成果针对有无轨道、引桥跨数、地震动特征、单一关键构件及墩高等对高速铁路桥梁-轨道系统的地震响应的影响[17]，而考虑两侧引桥与路基的高速铁路连续梁桥-轨道结构的整体系统在地震作用下的损伤规律的研究较少。因此，本文采用有限元软件ANSYS_APDL建立HBBSS仿真模型，分析HBBSS中各关键构件的地震损伤规律及刚度不确定性对HBBSS地震响应的影响规律。

1 HBBSS各关键构件地震响应规律

为明确HBBSS中各关键构件的地震响应及损伤规律，建立如图1所示的考虑引桥与路基的高速铁路连续梁桥-CRTSⅡ板式无砟轨道结构整体系统，桥梁结构参数见文献[18]。CRTSⅡ板式无砟轨道系统各关键构件包括扣件、剪切钢筋、CA砂浆层、侧向挡块、剪力齿槽、滑动层、硬质泡沫塑料、端刺、摩擦板等[19]，现结合CRTSⅡ板式无砟轨道设计原理[2]及已有研究取各关键构件参数[20-21]。选取近场EL Centro和Taft地震动，地震输入为一致激励，并调幅至9度多遇、设计和罕遇[22]。限于篇幅，仅绘制罕遇地震作用下各关键构件的坐标里程-地震响应幅值包络图，如图2所示。

图1 考虑引桥与路基的高速铁路连续梁桥-CRTSⅡ板式无砟轨道结构整体系统

图2 HBBSS中各关键构件地震响应规律

由图2可以发现，两种罕遇地震作用下，各关键构件变形规律趋于一致。滑动层产生的纵向变形最大，变形包络图峰值出现在桥跨的活动支座处，最大变形峰值发生在连续梁右边跨的活动支座处，EL Centro波和Taft波作用下的最大变形峰值分别达33 mm和58 mm；由于固定支座处的剪力齿槽对滑动层具有显著的约束效应，固定支座附近的滑动层纵向变形较小。连续梁与引桥相比，其跨度更长、质量更大、受到的地震惯性力更大，因此连续梁上的滑动层纵向变形总体上比引桥上的滑动层纵向变形更大。CA砂浆层的纵向变形包络曲线关于跨中近似成正对称分布，由于端刺及固定支座承受了极大的纵向力，端刺及固定支座处均出现纵向的显著位移峰值，且纵向位移最大值出现在连续梁制动墩上的固定支座处，EL Centro波和Taft波作用下的最大值分别为13 mm和34 mm；扣件的纵向变形规律与CA砂浆层相似，在端刺及固定支座处均出现纵向位移峰值，最大值出现在连续梁左边墩上的支座附近，最大接近1 mm(EL Centro)，2 mm(Taft)；梁缝处的剪切钢筋纵向变形最大峰值出现在右边引桥的梁缝处，EL Centro波和Taft波作用下的最大值分别1.3 mm和7.5 mm；剪力齿槽纵向变形最大峰值出现在连续梁制动墩上的固定支座处，最大仅为0.02 mm，因此剪力齿槽纵向变形可忽略。

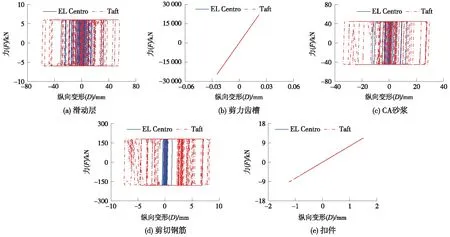
图3 HBBSS中各关键构件损伤规律

综上可知，CA砂浆及扣件纵向变形比滑动层小，归其原因为滑动层类似桥面上浮体系，地震作用下滑动层仅传递纵向摩擦力而产生较大位移，从而达到减震耗能的作用。此外，地震作用下连续梁制动墩和非制动墩均承受着较大的纵向剪力[23-25]。调整EL Centro波和Taft波的加速度峰值，并对3种水准地震下各关键构件的位移峰值进行计算，计算结果见表1、表2，其中9度罕遇地震下各关键构件的内力-位移关系曲线如图3所示。表1、表2中变形系数为地震下各关键构件的变形峰值/弹性限值(变形峰值为地震作用下各关键构件的进入非线性后的位移的最大值；弹性限值为各关键构件本构模型屈服点对应的位移值)。由图3、表1及表2可知，在3种水准EL Centro和Taft地震动作用下，各关键构件出现损伤的顺序基本一致，即滑动层、CA砂浆和剪切钢筋；剪力齿槽和扣件在设计水准下未损伤。对于变形系数较大的构件，设计时应重点关注。

表1 3种水准下各关键构件纵向变形程度(EL Centro)

表2 3种水准下各关键构件纵向变形程度(Taft)

2 HBBSS各关键构件刚度变化对体系地震响应的影响分析

竖向刚度保持不变，对不同水平刚度的各关键构件在9度罕遇地震作用下的地震响应进行计算，计算结果如图4所示。图4中，kca、kjq、kkj、kcc、kdc和khd分别为CA砂浆层、剪切钢筋、扣件、剪力齿槽、端刺与滑动层的水平刚度。

由图4可看出：对扣件地震响应的影响最显著是扣件刚度值，影响幅度达218%，其次是CA砂浆，影响幅度达148%，滑动层和剪切钢筋的影响幅度分别达到51%和35%，而端刺和剪力齿槽对扣件地震响应的影响很小；对剪力齿槽地震响应影响最大的是剪力齿槽刚度值，影响幅度达101%， 其次是滑动层和CA砂浆，影响幅度达14%，剪切钢筋、扣件及端刺对剪力齿槽地震响应的影响均很小；对CA砂浆地震响应影响最大的也是CA砂浆刚度值，影响幅度达320%，其次剪切钢筋为90%，滑动层为40%，而扣件、端刺及剪力齿槽均很小。对滑动层地震响应影响最大的是剪力齿槽刚度值，影响幅度达100%，其次滑动层和CA砂浆为10%左右，剪切钢筋、扣件及端刺的影响均很小；对剪切钢筋地震响应影响最大的是CA砂浆，影响幅度高达390%，其次剪切钢筋为133%，滑动层为30%，扣件、剪力齿槽及端刺的影响均很小。

图4 各关键构件刚度不确定性对体系地震响应的影响

综上所述，CA砂浆和滑动层对各关键构件地震响应均有显著的影响，CA砂浆层的影响尤为突出；此外，剪切钢筋对CA砂浆及其自身的地震响应也有一定的影响，究其原因为剪切钢筋是将轨道板、CA砂浆层及底座板联系在一起的层间关键抗剪构件。因此，CA砂浆、滑动层及剪切钢筋是各关键构件地震响应的重要影响因素，在抗震设计中应特别注意。

3 结论

建立了考虑钢轨、扣件、轨道板、CA砂浆、底座板、滑动层、桥梁、侧向挡块、固结机构、大小端刺等的考虑引桥与路基的高速铁路CRTSⅡ型板式无砟轨道-连续梁桥仿真模型，探讨了桥上CRTSⅡ型无砟轨道层间关键构件地震响应规律，结论如下。

(1)在3种地震强度下，进入损伤的关键构件按变形系数大小可划分为滑动层、CA砂浆和剪切钢筋。剪力齿槽和扣件在设计标准规定的地震动烈度下很难出现损伤。对于变形系数较大的构件，在设计分析时应予以重点关注。

(2)CA砂浆的纵向变形包络曲线关于跨中近似成正对称分布，由于端刺及固定支座承受了极大的纵向力，端刺及固定支座处均出现纵向极大位移峰值，且纵向位移最大值出现在连续梁制动墩上的固定支座处。

(3)CA砂浆、滑动层及剪切钢筋的刚度变化对各关键构件的地震响应具有显著影响，是各关键构件地震响应的重要影响因素，在抗震设计中应特别注意。

(4)地震作用下滑动层及滑动支座产生较大幅值的纵向滑移且滞回曲线中有较多的往复作用，从而具有显著的地震耗能作用。

(5)随着地震动强度的增大，各关键构件的地震变形系数显著增大。