Method for extracting angle-domain common image gathers in Kirchhoff beam migration

ZHANG Zhihou, YAO Yu, SUN Hui, 2*, YANG Junjie and LI Meng

1. Faculty of Geosciences and Environmental Engineering, Southwest Jiaotong University, Chengdu 611756, China;2. School of Resources and Environment, University of Electronic Science and Technology of China, Chengdu 611731, China

Abstract: Kirchhoff beam migration is a simplified Gaussian beam migration, which omits the dynamic information and can calculate multi-arrival traveltime, so it is a high-precision and fast seismic imaging method. In the imaging process, extracting common image gathers can be used for velocity analysis, improving the accuracy of modeling and imaging quality. Compared with the conventional common image gathers extracting methods, the angle-domain common image gathers extracting method can avoid the artifacts caused by multi-arrival seismic waves. The authors present a new method of extracting common image gathers in angle-domain from Kirchhoff beam migration and verify the method by numerical calculations.

Keywords: Kirchhoff beam migration; angle-domain common image gathers; beam propagator; travel time calculation

0 Introduction

Prestack depth migration methods can mainly be divided into wave equation based imaging method and ray-based imaging method. Ray-based migration methods can be further divided into Kirchhoff migration and beam migration. Beam migration methods boast the advantages of high computational efficiency and high accuracy. The Kirchhoff beam migration addressed in this paper belongs to the beam migration methods.

Hill introduced the Gaussian beam poststack migration and Gaussian beam prestack migration in 1990 and 2001, respectively, which laid the foundation of beam migration methods. Sunetal. (2000) combined the idea of beam imaging with Kirchhoff migration theory, and proposed a 3-D Kirchhoff beam migration method. Gray (2005) put forward the Gaus-sian beam migration in the shot domain, and made a simple statement for the Gaussian beam migration under the complex surface. Gray and Bleistein (2009) proposed true-amplitude Gaussian beam migration based on convolutional imaging conditions. Popovetal. (2010) proposed a Gaussian beam superposition imaging method, which has better calculation accuracy but lower calculation efficiency. Liu and Palachala (2011) simplified the Gaussian beam migration, only keeping its kinematic characteristics, and provided a new beam propagation operator and weight function to further improve the calculation efficiency of the migration algorithm. Huangetal. (2016) introduced Fresnel beam propagation operator into Gaussian beam migration to solve the problem that Gaussian beam spreads rapidly with the increase of propagation distance. Yuanetal. (2017) proposed the least-square Gaussian beam migration imaging method by combining Gaussian beam migration with Gaussian beam forward modeling method. Sunetal. (2018) studied the beam propagation operator and local plane wave decomposition method in Kirchhoff beam migration.

The extraction of common image gathers is an important means of seismic data processing, which is of great significance to velocity analysis and image quality improvement. Xuetal. (2001) pointed out that Kirchhoff migration can be carried out in the angle-domain for complex models, so that the migration noise can be suppressed better. Meanwhile, it is suggested to extract the angle-domain common image gathers to avoid the artifacts caused by multiple wavefields. Xieetal. (2002) proposed a method of angle-domain common image gathers extraction based on the decomposition of local plane waves. Rickett and Sava (2002) proposed a method to obtain the common offset image gathers from the offset domain, and further proposed a method to obtain the angle common image gathers through the offset domain imaging gathers. The essence of this method is to obtain the angle ga-thers by using the time shift migration imaging conditions. Sava and Fomel (2003) carried out a further study on the method of obtaining the common image gathers in angle-domain through the offset domain common image gathers and provided a transformation post migration method, which transformed the common image gathers in offset domain into the common image gathers in angle-domain through the slant stacking method. Soubaras (2003) presented a method to obtain the angle gathers of the shot gathers by using the harmonic ferocity method. Fomel (2004) provi-ded the method of obtaining the angle-domain common image gathers from the three-dimensional wave equation imaging. Sava and Fomel (2006) proposed the me-thod of extracting common image gathers in angle-domain based on time-shifting imaging conditions. Lietal. (2008) proposed a method of accurately exac-ting common image gathers in angle-domain in wave equation migration and applied it to stack imaging method. Lietal. (2017) proposed a method for extracting common image gathers in angle-domain based on local plane wave decomposition in reverse time migration. Song and Liu (2018) extracted the common image gathers in the angle-domain in the VSP RTM.

Kirchhoff beam migration is one of the beam migration methods. Extracting common image gathers in angle-domain is not as complicated as wave equation migration methods. The imaging angles of underground nodes can be calculated and obtained during the implementation of the migration. The study introduces a method of calculating this imaging angle and verify it by extracting angle-domain common image gathers of the complex model.

1 Methods and principles

Calculating the imaging angle of the target nodes is the key step in extracting the common image gathers in the angle-domain. In this section, we will introduce the beam propagation operator of Kirchhoff beam migration and the calculation method of the target nodes’ imaging angle.

1.1 Beam propagation operator

Kirchhoff beam migration ignores the dynamic information in the process of ray tracing, so it is impossible to calculate the beam width as Gaussian beam. As shown in Fig.1, Liu and Palacharla (2011) calculated the beam width with the following equation:

(1)

WhereV0is the velocity at the starting position of the ray,Δais the angle interval between adjacent rays, andσis the integral of velocityValong the ray path, which can be expressed as:

(2)

Fig.1 Schematic diagram of ray width (after Liu & Palacharla, 2011)

The grid node’s traveltime in the beam is obtained by Taylor expansion of the discrete node’s information on the central ray. As shown in Fig.2,xis the target point covered by the beam,x0is the closest point toxon the central ray,x′ is the projection ofxon the central ray, and the distance betweenxandx0in Cartesian coordinate system isΔxandΔz, respectively, the distance betweenxandx0in the ray central coordinate system isΔsandΔn, respectively, the traveltime of the central ray atx0isT(x0), and the traveltimeT(x) atxcan be expressed as:

(3)

(4)

Wherepxandpzare the slowness components atx0, respectively.

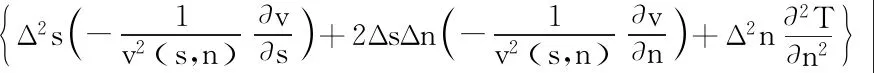
(5)

Wherev(s,n) represents the velocity at pointx0. Taking into account the transformation relationship between the central ray coordinate system and the Cartesian coordinate system:

Δs=sinθΔx+cosθΔz

(6)

Δn=cosθΔx-sinθΔz

(7)

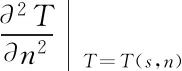
(8)

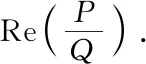
(9)

Whereσ0is

(10)

Combining the above formula, the traveltimeT(x) of the beam at the target nodexcan be obtained.

Fig.2 Schematic diagram of grid point traveltime calculation

After obtaining the travel time information, the slowness componentspx(x) andpz(x) can be obtained by calculating the partial derivatives to the spatial position：

(11)

(12)

In this way, the propagation angleαof the beam at the target node can be obtained:

(13)

Fig.3 Schematic diagram of imaging angle calculation

Fig.4 Velocity distribution of Marmousi model

(a) Common image gathers extraction locations; (b) common image gathers (CDP: 250); (c) common image gathers (CDP: 350); (d) common image gathers (CDP: 450); (e) common image gathers (CDP: 550); (f) common image gathers (CDP: 650).Fig.5 Extraction of angle-domain common image gathers from Marmousi model

As shown in Fig.3, after knowing the propagation anglesθSandθBCof the ray beam from the source and the window center to the target node, the imaging angleθof the node can be obtained by subtracting the two angles.

θ=|θS-θBC|

(14)

2 Numerical experiment

In this section, we use the Marmousi data sets to verify the angle-domain common image gathers from Kirchhoff beam migration.

Fig.4 shows the velocity distribution of Marmousi model. There are 737 grid points in the transverse direction of the model, the grid spacing is 12.5 m, 750 grid points in the longitudinal direction, and the grid spacing is 4.0 m. The velocity of Marmousi model varies drama-tically and the model contains many faults.

Fig.5 shows the results of angle-domain common image gathers from the Marmousi model. Fig.5a shows the imaging results of the model and the CDP locations of the extracted angle-domain common image gathers. Fig.5b-f shows the common image gathers of CDP numbers 250, 350, 450, 550 and 650, respectively, with the maximum imaging angle of the grid nodes of 120°. It can be seen from Fig.5 that the imaging results strictly match the velocity model. The angle-domain common image gathers extracted by the method in this paper are basically with flat layers, which reflects the effectiveness of the method in this paper.

3 Conclusion

In this paper, a new extracting method of angle-domain common image gathers for Kirchhoff beam migration is presented. The key step of extracting angle-domain common image gathers is how to obtain the imaging angle of the target nodes. In Kirchhoff beam migration, it is necessary to calculate the propagation angle of the beam from the shot point and the window center at the target node respectively. Although the dynamic information is omitted in the ray tracing process, the influence of wave front curvature on the grid nodes’ traveltime is eliminated by an approximation calculation method. The propagation angles of the beam at the grid nodes can be accurately calculated. The numerical results of Marmousi data sets verify the effectiveness of the proposed method.