协调解决暂态稳定与短路电流问题的最优阻抗运行策略

贺忠尉，向 勇，邓明辉，阳 帅,黄文涛*，何 俊

(1.国网湖北省电力有限公司恩施供电公司，湖北 恩施 445000；2.湖北工业大学 电气与电子工程学院，武汉 430000)

为加快推动能源生产和消费革命，进一步提升煤电高效清洁发展水平.同时满足大规模跨区输电和新能源发电并网的要求，中国国务院提出“上大压小”的政策[1]，促使了越来越多大容量发电机组在低电压等级电网中投运，大容量发电机组具有效率高、经济性好等优点，同时能够减少大气污染物的排放,对于节能降耗,具有重要经济和环境效益[2].大容量机组下移到低等级电网，对低等级电网的暂态稳定以及短路电流都会有不同程度的影响.对于大容量机组接入低等级电网后，从理论上分析暂态稳定问题，发电机经联络线外送功率，外部条件相同的情况下，发电机外送功率越大，暂态稳定裕度越低，越易发生暂稳问题;发电机组与系统间容易失去同步运行，导致暂态失稳；若为了保持暂态稳定，通过串联电容的方式减小回路阻抗，暂态稳定的稳定问题得以缓解，但同时会增大电网母线短路电流，易导致短路电流超标.因此，暂态稳定和短路电流问题是一对相互矛盾的问题.

目前国内外研究文献中还没有提出具体的解决办法来平衡大容量机组下移低等级电网导致的暂态稳定与短路电流之间的矛盾问题.对于电网短路电流超标的问题，陈伟等[3]提出的通过从优化电网运行方式、加装变压器中性点小电抗和新型限流设备的应用等方面展开分析，最后提出适应当前区域的短路电流综合治理方案.Zhang等[4]针对500 kV高压接收端电网三相短路电流，提出了在特高压变电站隔离500 kV母线，将变电站外的线路搭接，并分散电源，从而限制短路电流超标.文献[5-6]分析了电网由于网架结构变化以及600 MW接入220 kV电网等原因导致短路电流超标的原因，提出了通过统一规划电网、采用高阻抗主变和限流电抗器、采用合理的电源接入方式等措施来防止短路电流超标.文献[7-10]研究的短路电流对电网结构强度的要求和对电网运行方式以及受电能力等因素的影响，将电网进行分区，调整运行方式，加强网架强度等；文献[11-12]研究了限制三相短路电流的控制策略.目前对于暂态稳定问题的研究中，管霖等[13]提出了基于节点暂态电压特征的区域划分方法，Zhang等[14]提出了通过建立具有RPG的互联电力系统的运动方程，然后推导暂态能量函数，以分析虚拟惯性对暂态能量转换的影响.Yuan等[15]提出通过重新安排同步发电机的运行同时保持瞬态稳定性以确保突发事件的发生.高昆仑等[16]提出了一种基于一维卷积神经网络(1D-CNN)的暂态稳定评估方法.Kishan等[17]通过调节暂态能量函数，开发了一种改进的新混合方法来加强系统的暂态稳定性.

这些文献中的研究方法都是单一针对解决暂态稳定问题或者短路电流问题，克服了其中的暂态稳定问题又会增大短路电流超标的风险，反之亦然.本文建立了电网短路电流水平和暂态稳定水平的表征电网稳定水平的协调优化目标函数，给出了约束条件.提出了基于外点罚函数法求解最优系统阻抗值来保证系统稳定运行的控制策略，该策略通过优化出系统最佳阻抗来同时解决电力系统中存在的暂态稳定与短路电流的问题，提升电力系统的安全稳定水平.

1 暂态稳定分析

在电力系统受到故障干扰后，忽略定子回路的非周期分量，功率特性变化如图1所示.

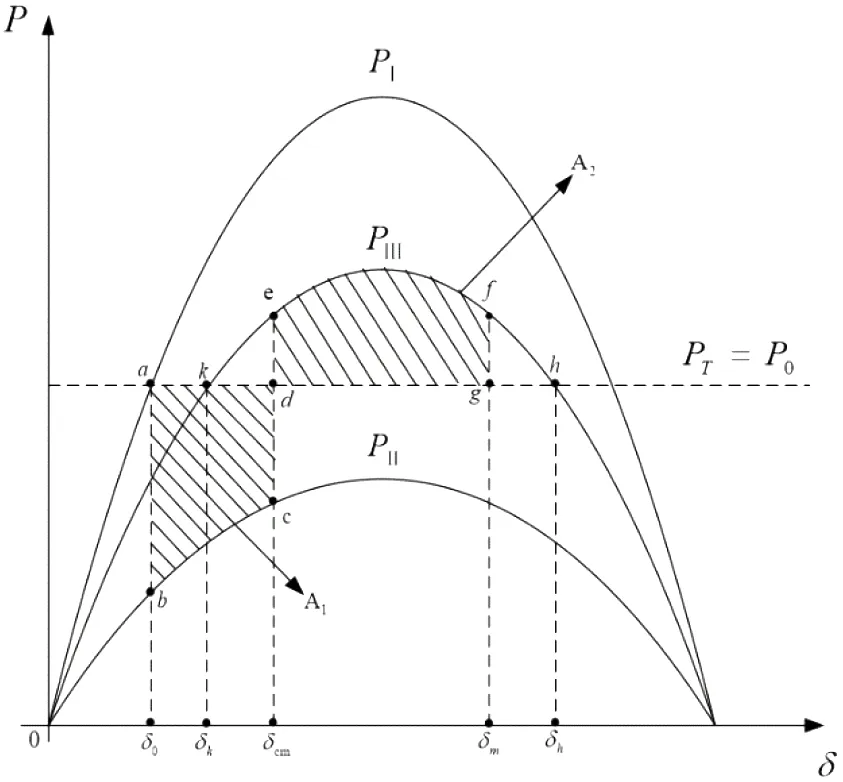
图1 简单系统三种状态的功角特性曲线Fig.1 Power angle characteristic curve of three states of simple system

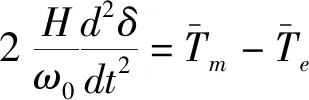
由功率特性曲线可知，系统的暂态稳定性与功率角的大小密切相关，系统受到扰动后功率角变化过程为[18]:

(1)

式中H为惯性时间常数，ω0为转子速度额定值，Tm为机械转矩，Te为电磁转矩.

正常运行时发电机经过变压器和线路向无限大系统送电，发电机用暂态电抗后的恒定电压来简化，则发电机电磁功率Pe和U功角关系为：

(2)

设用函数δ(X)表示系统等值阻抗和功角关系为：

(3)

式中C1、C2均为正常数，Pe为发电机电磁功率，E′为发电机等值电动势，X为电动势E′与无限大系统之间电抗，δ为功率角，U为系统电压.

由于δ(X)的导函数为：

(4)

δ′(X)恒大于零，即系统的等值阻抗与功率角正相关.

由此可知，适当的调节系统等值阻抗X，可以有效的调节功率角δ，从而保证电力系统的稳定运行.

2 短路电流分析

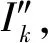
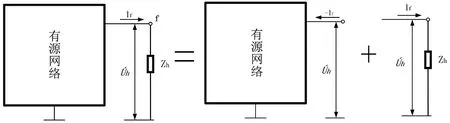
图2 短路电流计算原理图Fig.2 Schematic diagram of short-circuit current calculation

本文采用短路电流的工程算法进行描述.忽略短路过程中的过渡阻抗，节点h的短路电流周期分量初始值表示为：

(5)

若从系统的等值阻抗分析，采用短路点自阻抗分析模型[19]可得到短路电流约束条件为[20]：

(6)

式中Amn为两个节点间互导纳，Ann为节点自导纳，gk为0-1变量表示线路或变压器的开闭状态，A为短路电流的导纳矩阵，X是A的逆矩阵表示电抗矩阵，Bcn为节点h处补偿电容器电纳，G为发电机，xG″为发电机次暂态电抗，xijk为以i、j为首末节点的线路k的电抗，I为节点集合，J为短路电流超标母线集合，Xhh为式(6)求出的节点自电抗，IA,h为节点h处短路电流基准值，ih,lim为h点短路电流最大限额.

由短路电流约束条件可得，在既有网架结构条件下，受电气距离以及发电机和变压器阻抗等因数影响，短路电流与系统阻抗呈负相关，通过串联电容器或者串联电抗器等影响系统阻抗的手段能有效调节系统短路电流.

3 暂态稳定与短路电流的耦合

在大机组下移到低等级电网的研究背景下，且在原有网架结构和运行方式下，易发生短路电流超标和暂态失稳等故障.设以系统阻抗表达暂态稳定的函数为式(3)，以系统阻抗表达短路电流的函数由式(5)可得为：

(7)

暂态稳定与短路电流受系统阻抗变化影响的变化趋势如图3所示,其中阻抗值为X1～X3时，S1区域表示系统暂态稳定；阻抗值X2～X4时，S2区域表示电流在限额范围内；阻抗值X2～X3时，S3区域表示暂态不失稳且短路电流不超标.

图3 暂态稳定与短路电流受系统阻抗影响变化趋势Fig.3 Transient stability and short-circuit current change trend affected by system impedance

设M(X)为保证系统稳定运行的函数,即为：

M=λ1F1+λ2F2+λ3,

(8)

(9)

(10)

式中λ1、λ2、λ3均为常数.

通过优化协调方法Np，在满足大机组下移低等级电网后暂态稳定和短路电流不超标条件下，得到保证系统安全稳定运行的最优系统阻抗值M.利用优化协调方法Np得到目标函数M最小，Np为：

Np=[Np1,Np2,Np3,…,NpN].

(11)

4 基于外点罚函数的最优系统阻抗值求解

根据式(8)～(10)可以得到目标函数M的表达式为：

(12)

等式约束为短路电流与系统阻抗的动态平衡关系以及功角与系统阻抗的动态平衡关系，极坐标下的潮流方程；不等式约束为在系统稳定运行的条件下，各个系统参数的限额范围.

外点罚函数的原理为根据约束的特点，构造惩罚函数，然后加到目标函数中去，将约束问题求解转化为一系列的无约束问题.这种“惩罚策略”，对于无约束问题求解过程中的那些企图违反约束条件的目标点给予惩罚.如图4所示.

图4 外点罚函数法原理图Fig.4 Principle diagram of the external point penalty function method

在寻求最优系统阻抗值时，采用一般的消元法无法解决过程中的约束非线性问题.为了在满足约束条件的情况下，使得目标函数值最小，即得到最优系统阻抗值，则需要利用极小化辅助函数将约束非线性问题转换为无约束问题.鉴于此，本文采用外点罚函数法来求解最优系统阻抗值[21].

外点罚函数约束问题为：

minf(x)，x∈Rn，

s.t.gi(x)≥0，i=1,2，…，u，

hj(x)=0，j=1,2，…，w.

(13)

式中f(x)、gi(x)、hj(x)均为Rn上的连续函数，状态变量为：

(14)

其中，δv为功角，Ir为短路电流.

根据式(12)确定目标函数为：

f(x)=M.

(15)

等式约束为：

(16)

不等式约束为：

(17)

其中，Ul,max、Pm,max、δv,max、Iw,max、Xk,max分别为系统电压、发电机组出力、功角、短路电流以及系统阻抗的最大值；Ul,max、Pm,min、δv,min、Iw,min、Xk,min分别为系统电压、发电机组出力、功角、短路电流以及系统阻抗的最小值.

通过将目标函数和约束函数组成辅助函数，将原来的约束问题转化为极小化辅助函数的无约束问题的途径，将式(13)优化为：

F(x，σ)=f(x)+σP(x).

(18)

式中P(x)具有以下形式：

(19)

φ和ψ是满足下列条件的连续函数：

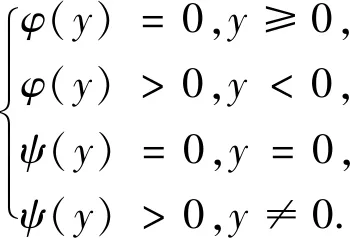
(20)

其中函数φ和ψ的典型取法为：

(21)

其中α≥1,β≥1,均为给定常数，通常取作α=β=2.由此将式(13)转化无约束问题：

(22)

其中σ是很大的正数，P(x)是连续函数.因此，从定义知，当x为可行点时，P(x)=0，从而有F(x，σ)=f(x)；当x不是可行点时，在x处，σP(x)是很大的正数，它的存在是对脱离可行域的一种惩罚，从而迫使迭代点靠近可行域.由此通过求解式(22)得到式(13)的近似解，这个过程中，随着σ增大，得到的近似解约接近于真实值.一般把σP(x)称为罚项，σ称为罚因子，F(x，σ)称为罚函数.

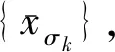
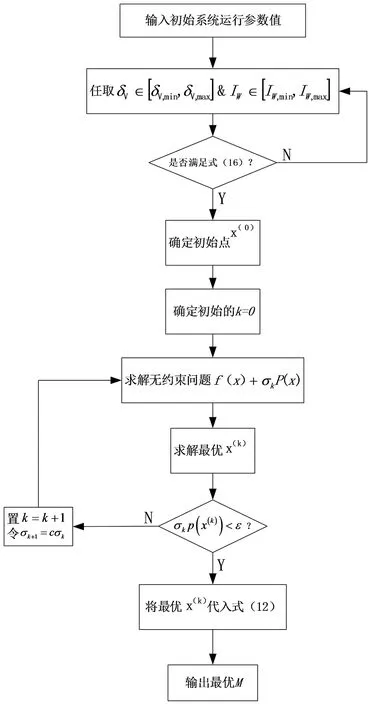
图5 最优系统阻抗值求解流程图Fig.5 Flow chart for solving the optimal system impedance value

已知约束问题，取控制误差ε>0以及罚因子的放大系数c>1，其中可取ε=10-4，c=10；

第1步：给定初始点x(0)和初始惩罚因子σ1，其中x(0)可以不是可行点，取σ1=1，令k=1；

第2步：以xk-1为初始点求解无约束问题：

minP(x，σk)=f(x)+σkP(x)

(23)

第3步：若σkp(x(k))<ε，那么以x(k)作为近似最优解，停止计算.否则，令σk+1=cσk，k=k+1，返回到第2步.

5 GGE电网仿真分析

采用HB电网2018年夏高运行方式下PSASP数据包为基础参数，以GGE地区电网为实例对上述策略进行仿真验证，GGE地区220 kV主网架如图6所示，其中天蓝色标识线路为重点仿真分析线路[22].

图6 GGE地区220 kV主网架图Fig.6 220 kV main grid in GGE area

EZ2号机组与4号机组容量均为650 MW，通过电厂出线串入GGE地区220 kV主网，电网出线同时也是联系WCB电网与EZ电网的主干通道.由于EZ2号机组与4号机组的机组容量大，且从图6中可知，EZ电网与WCB电网的电气距离短，两台大容量机组直接连入220 kV电网，对GGE地区电网的安全稳定运行存在潜在的失稳风险，尤其是容易发生短路电流超标与暂态失稳.

根据文中所述的短路电流与暂态稳定协调控制策略，以EZ2、G4、LZ之间的电气联系为重点仿真对象，根据式(12)求解得到系统最优阻抗值的条件下，鄂光线与鄂庄线的阻抗分别为：

(24)

其中ZEG为鄂光线最优阻抗值，ZEZ为鄂庄线最优阻抗值，单位为104Ω.

设计8种方案下鄂光线与鄂庄线的不同阻抗值进行仿真验证.阻抗值如表1所示.

表1 重点仿真线路在8种方案下的阻抗值Tab.1 Impedance values of key simulation lines under 8 schemes

根据本文所提出的策略以及对算法的求解，如表1所示，将方案8设定为通过外点罚函数寻得的系统最优阻抗值，以最优阻抗为基准，在一定范围内设定7种不同的系统阻抗值，通过PSASP显示高于或低于系统最优阻抗的仿真结果，并对暂态稳定以及短路电流进行分析，将结果与方案8进行比较，来验证本文所提策略的有效性与可行性.

将方案1至方案4中的阻抗值代入PSASP中进行仿真，仿真结果如图7～12和图13～16所示.

图7 2号机组功角曲线 图8 4号机组功角曲线Fig.7 Unit 2 power angle curve Fig.8 Unit 4 power angle curve

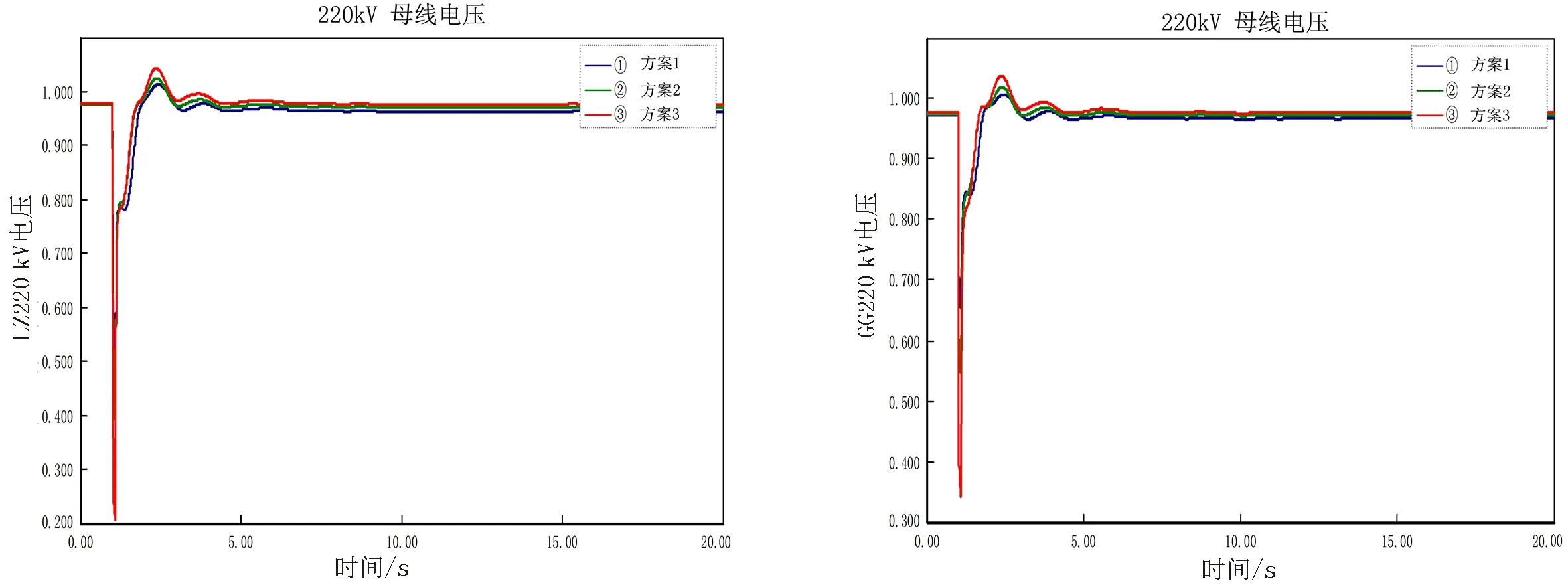
图9 LZ 220 kV电压曲线 图10 GG 220 kV电压曲线Fig.9 LZ 220 kV voltage curve Fig.9 GG 220 kV voltage curve

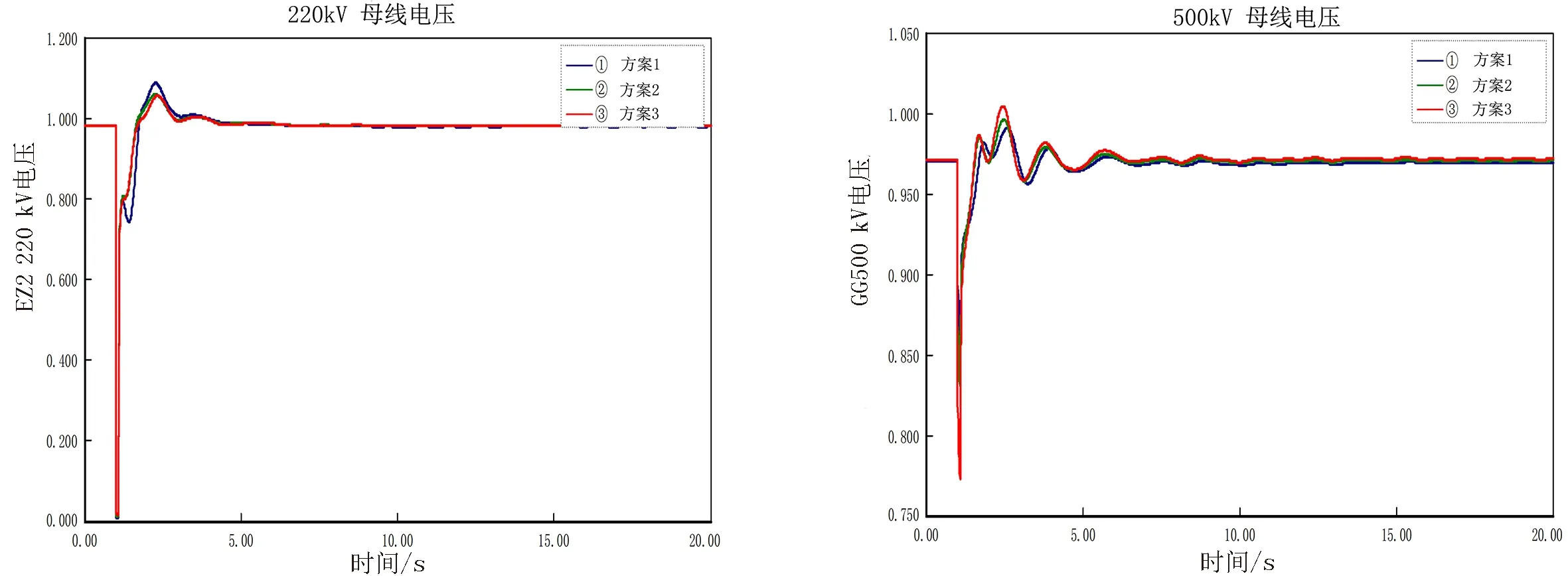
图11 EZ2 220 kV电压曲线 图12 GG500kV电压曲线Fig.11 EZ2 220 kV voltage curve Fig.12 GG 500 kV voltage curve

方案1至方案3的仿真结果如图7～12所示，以图中①～③曲线表示随系统阻抗值逐渐增大，功角、电压振幅逐渐增大，随着系统阻抗值逐渐增大到濒临暂态失稳的过程中，EZ2机组功角、LZ 220 kV电压、EZ2 220 kV电压、GG 220 kV电压、GG 500 kV电压均在稳定范围内，但振幅逐渐增大，短路电流不超标，逐渐威胁到系统暂态稳定.

方案4中的阻抗值代入进行仿真，最终如图13～16所示，EZ2机组功角失稳，LZ、GG、EZ 2220 kV电压以及GG 500 kV电压均失稳，由于阻抗值偏大，系统发生暂态失稳.

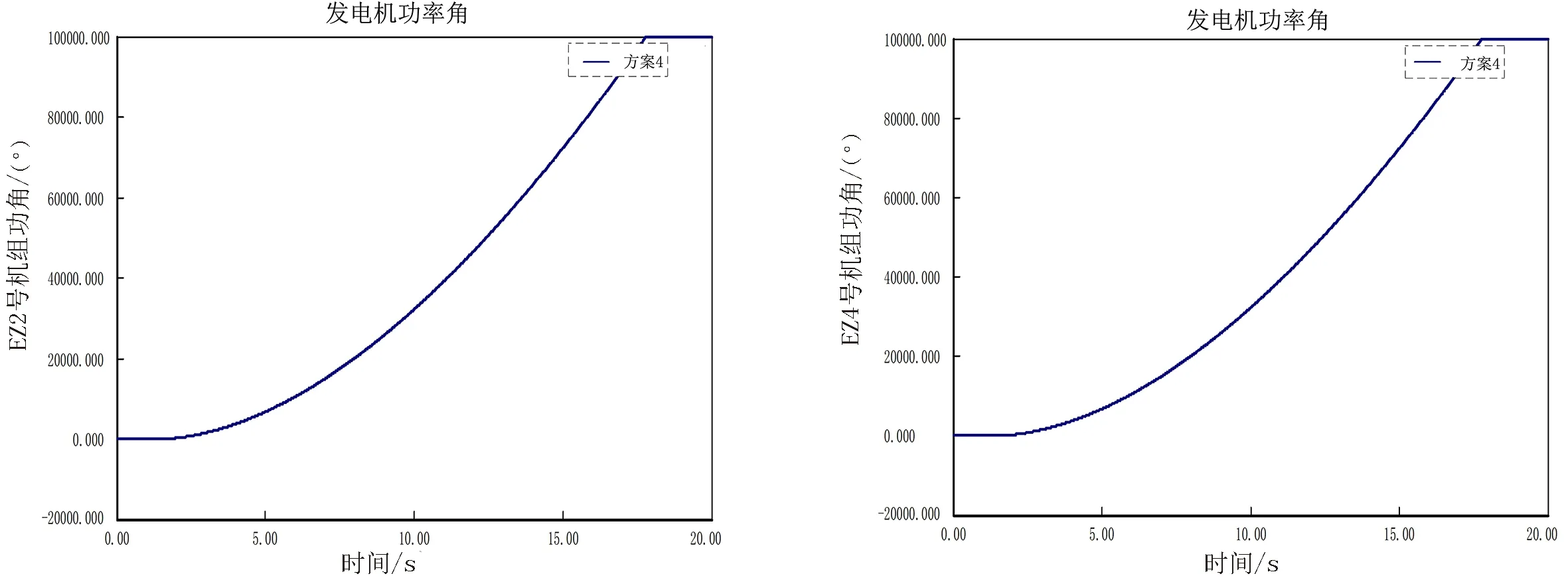
图13 2号机组功角曲线 图14 4号机组功角曲线Fig.13 Unit 2 power angle curve Fig.13 Unit 4 power angle curve

将方案5至方案7中的阻抗值代入PSASP中进行仿真，仿真结果如图17～22所示.

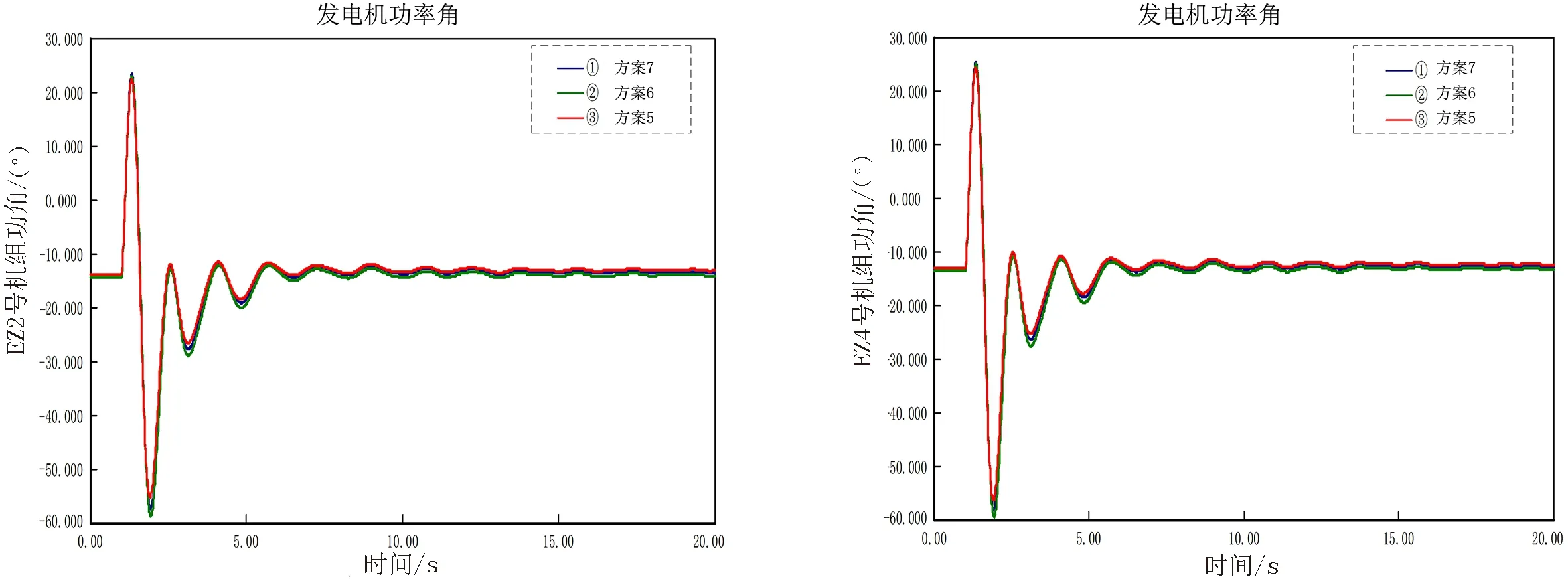
图17 2号机组功角曲线 图18 4号机组功角曲线Fig.17 Unit 2 power angle curve Fig.18 Unit 4 power angle curve

由图可知，系统阻抗值逐渐减小，以①～③曲线表示，LZ、GG、EZ2 220 kV电压以及GG 500 kV电压均稳定，系统暂态稳定，但短路电流超标.

将方案8中的阻抗值代入PSASP中进行仿真，计算结果如图10(a)～10(d)所示.

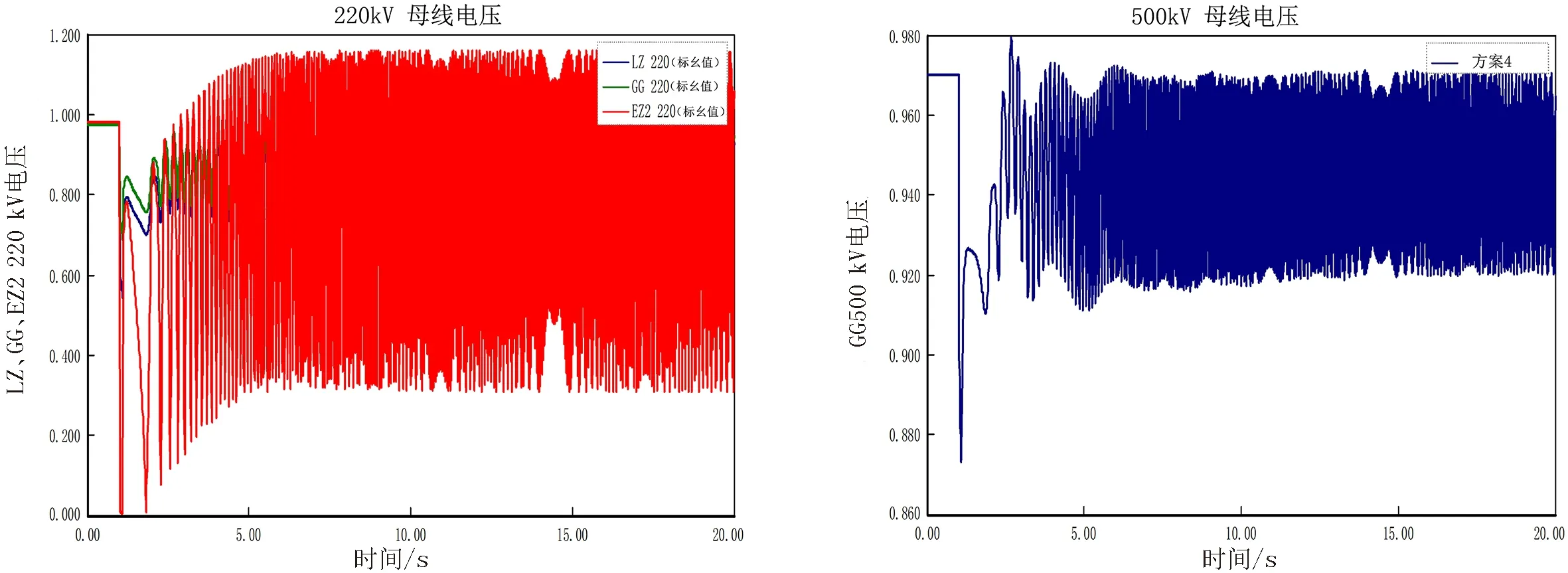
图15 LZ、GG、EZ2 220 kV电压曲线 图16 GG 500 kV电压曲线Fig.15 220 kV voltage curve of LZ,GG,EZ2 Fig.16 GG 500 kV voltage curve

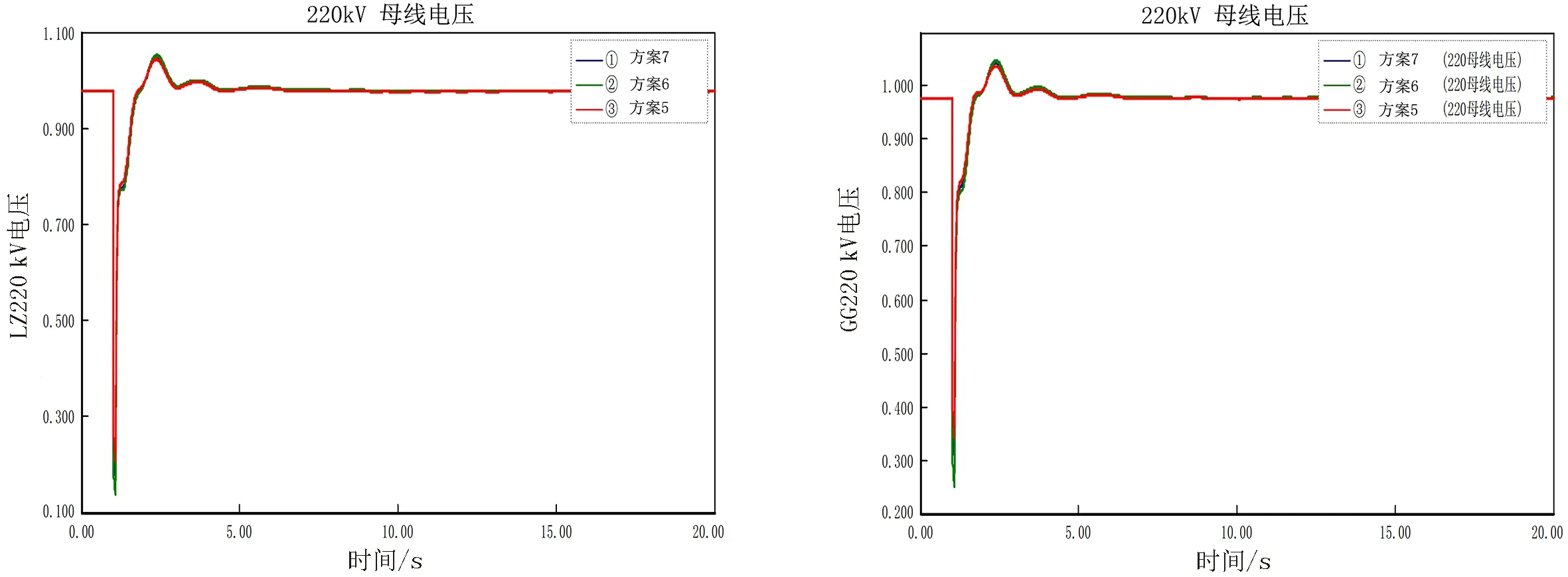
图19 LZ 220 kV电压曲线 图20 GG 220 kV电压曲线Fig.19 LZ 220 kV voltage curve Fig.20 GG 220 kV voltage curve

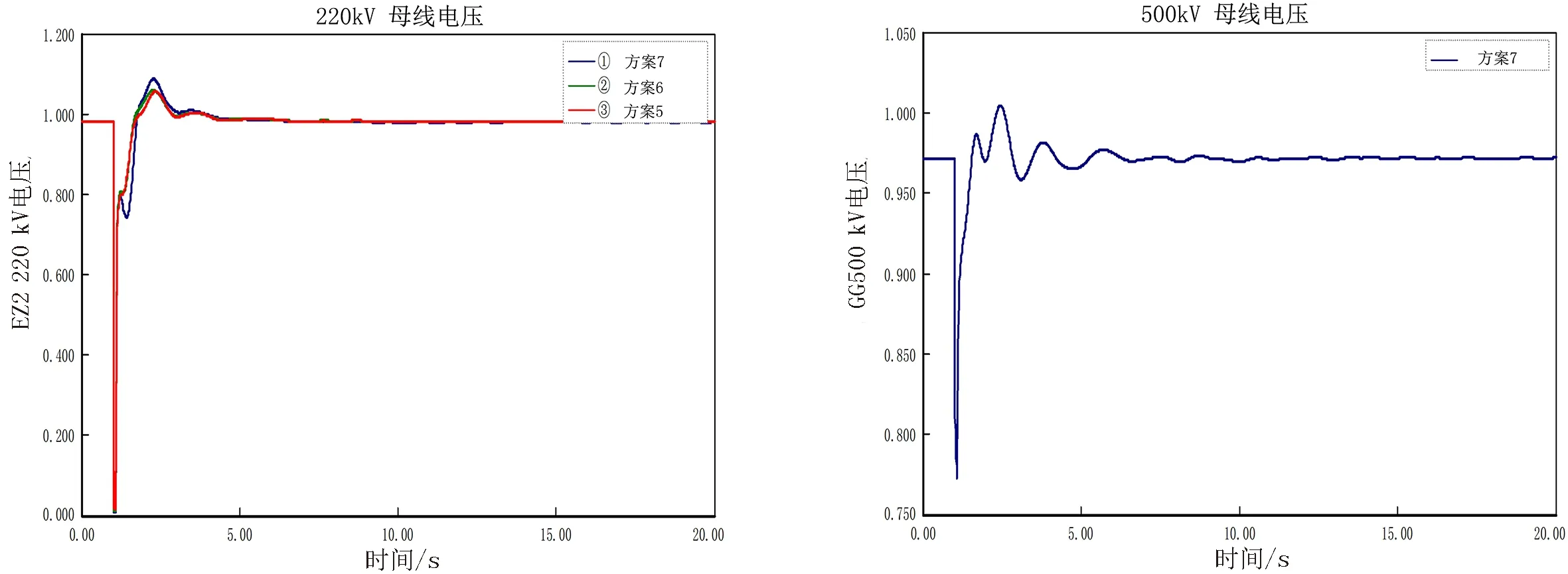
图21 EZ2 220 kV电压曲线 图22 GG 500 kV电压曲线Fig.21 EZ2 220 kV voltage curve Fig.22 GG 500 kV voltage curve

如图23～26所示，采用本文所提策略得到的系统阻抗值进行仿真验证，系统保持稳定运行.方案1～方案8所有仿真结果分析如表2所示.

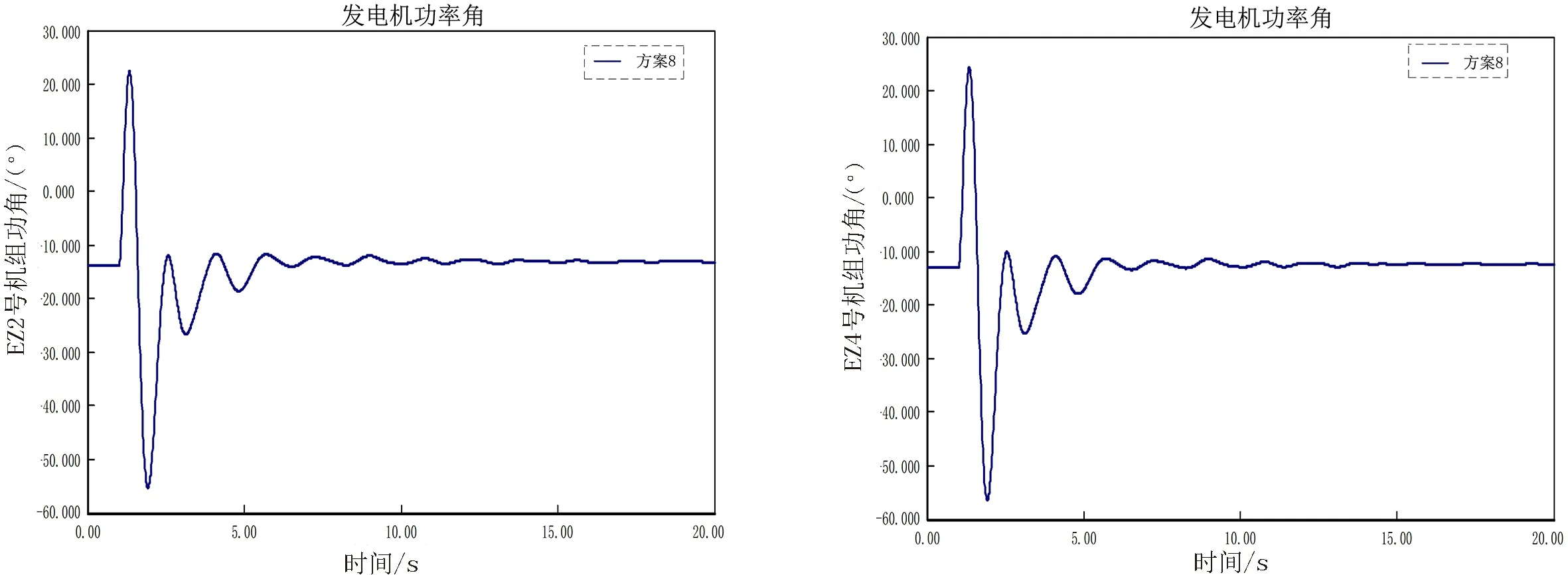
图23 2号机组功角曲线 图24 4号机组功角曲线Fig.23 Unit 2 power angle curve Fig.24 Unit 4 power angle curve

表2 仿真结果分析表Tab.2 Simulation results analysis

仿真结果表明，本文提出的暂态稳定与协调控制策略能有效的解决大机组下移低等级电网状况下，暂态稳定与短路电流的矛盾问题，保障系统稳定运行.

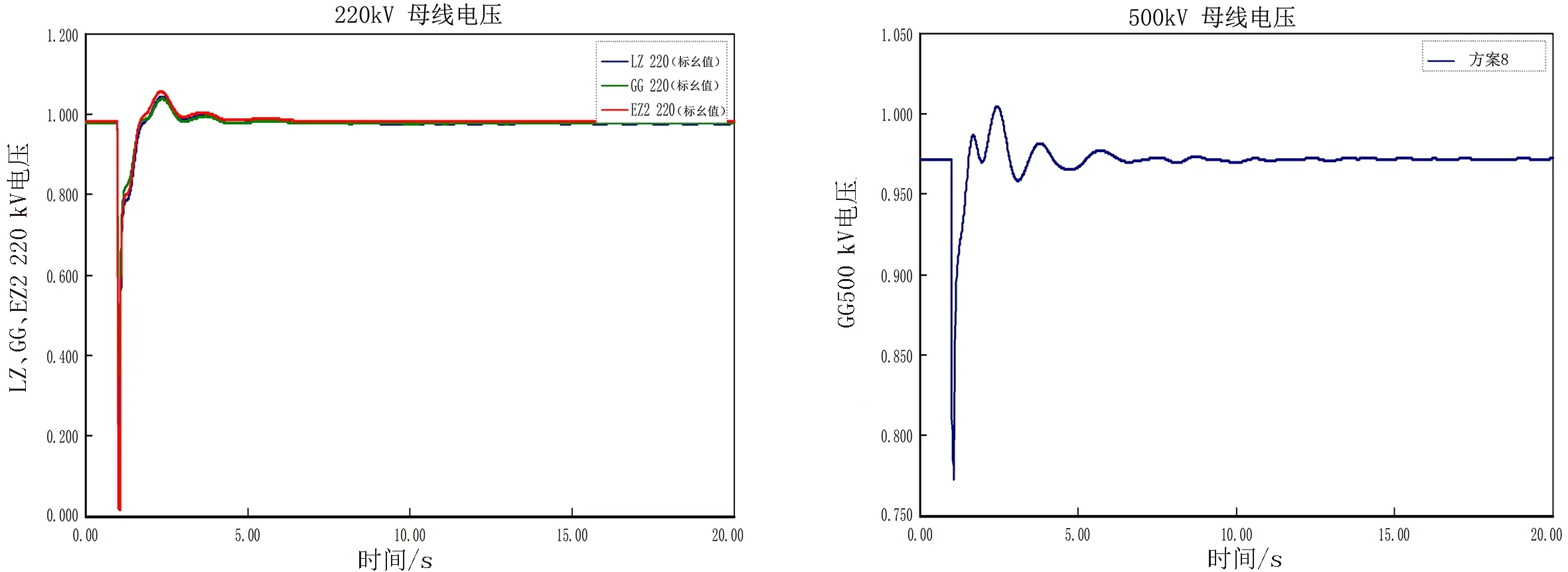
图25 LZ、GG、EZ2 220 kV电压曲线 图26 GG 500 kV电压曲线Fig.25 220 kV voltage curve of LZ,GG,EZ2 Fig.26 GG 500 kV voltage curve

6 结语

对于传统的通过切机、切负荷等措施来解决短路电流超标和暂态失稳等系统稳定问题，会使得经济效益变差，且不能从根本上协调解决二者之间的矛盾.本文建立联系暂态稳定与短路电流的数学模型，采用外点罚函数法求解系统最优阻抗值，从保证了系统的稳定运行.这为大机组下移低等级电网，引发的暂态稳定与短路电流超标等问题提供了一个可靠的理论依据和解决措施.