一类等价商范畴的构造

毕梦凡 ，何济位

(杭州师范大学理学院，浙江 杭州 311121)

0 引言

设K为特征是零的域, 设A=A0⊕A1⊕A2⊕…为诺特分次K-代数.记grA为有限生成的分次右A-模构成的范畴, 记torA为有限维分次右A-模构成的grA的全子范畴.由于torA是grA的Serre子范畴, 故有商范畴qgrA=grA/torA.在非交换射影几何中, 商范畴qgrA通常被称为非交换射影概形[1].事实上, 若A=K[x0,x1,...,xn]为多项式代数, 则qgrA等价于射影空间Pn的凝聚层范畴[2].

在非交换射影代数几何的研究中, 需要将一个诺特分次代数的商范畴用其他代数的商范畴来刻画.比如, 任意一个诺特连通分次代数A的商范畴qgrA必定等价于其Veronese子代数A(n)的商范畴qgrA(n)[1,3-4],而代数A(n)具有良好的同调性质,当n足够大时,A(n)是一个Koszul代数.在非交换奇点解消理论中,需要将Gorenstein代数的商范畴用某个自反模的自同态代数的商范畴来刻画[5-6].在文献[7]和[8]中,本文通信作者与其合作者建立了商范畴的Galois理论,从而为非交换奇点解消提供一类工具.特别地,对于Gorenstein商奇点是2维时,其所有奇点解消都是Morita等价于斜群代数[5].

本文的主要目的是通过矩阵方法,由一个给定诺特分次代数A来构造一类新的代数,而这类新构造的代数与分次代数A的商范畴是等价的.在新构造的代数中,有一类具有Koszul性质.Koszul代数是一类具有很好同调性质的分次代数,其在量子群、代数几何、代数表示理论等领域有重要应用[9-11].在非交换射影几何的研究中,需要应用非连通的Koszul代数(即A0不是半单代数[12]).本文通过矩阵方法,从已有连通Koszul代数构造了一类A0不是半单的Koszul代数.

1 准备知识

令K为特征是0的域.本文所讨论的分次代数都是指分次空间A=⊕n≥0An上具有一个代数结构,并且其乘积满足:对于任意元素aAi,b∈Aj,都有ab∈Ai+j,其中i,j≥0.称一个分次代数是局部有限的,如果对于任意i≥0,dim(Ai)<∈.称分次代数A是右诺特的,如果A的分次右理想满足升链条件.如果A0=K,则称分次代数A为连通分次代数.

一个分次右A-模M是一个分次空间⊕n∈ZMn以及右A-作用满足:对于任意m∈Mi,a∈Aj都有ma∈Mi+j,其中,i∈Z,j∈N.一个分次模同态是指一个右A-模同态f:M→N,满足f(m)∈Ni,∀m∈Mi,i∈Z.

令A为局部有限的右诺特分次代数.记grA为有限生成的分次右A-模构成的范畴,其态射为分次模同态.令torA为有限维分次右A-模构成grA的全子范畴.定义商范畴:

qgrA=grA/torA.

由于A是诺特分次代数,商范畴qgrA是Abel范畴.

对于一个分次代数A,可以将A0看成是分次右A-模.称A是Koszul代数,如果分次模A0有一个投射模分解:

…→Pn→…→P1→P0→A0→0,

其中,对于任意n≥0,分次模Pn是由n次元生成的.比如,多项式代数与外代数都是连通Koszul代数.本文将构造一类非连通的Koszul代数.

2 矩阵代数

设A是诺特分次代数,设I为A的分次双边理想.称I为余有限的,如果A/I是有限维的.

任意给定A的分次双边理想I,构作矩阵代数

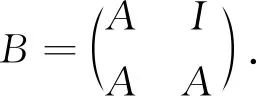
(1)

引理1设A为分次代数,I为A的余有限的双边理想.令B为如上定义的代数,

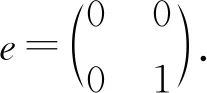
证明eBe≅A是显然的.另一方面,

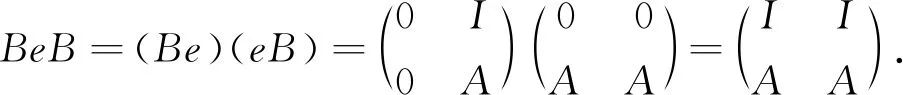
由于I是余有限的，故B/BeB是有限维的.证毕.

引理2若A为右诺特分次代数,则矩阵代数B也是右诺特分次代数.

证明作映射

f:A→B,a

则f是一个分次代数同态,并且f是单射.因此可以将A看作是B的子代数,由此B是分次右A-模.作为右A-模,B可以写作

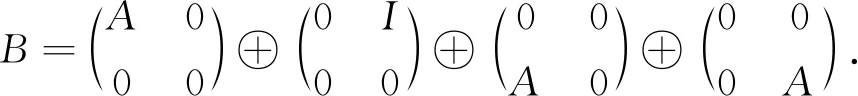
由于A是右诺特的,上述等式右边的每一个直和项都是有限生成的,故B是有限生成的右A-模.再由A是右诺特代数,可得出B也是右诺特代数.证毕.

命题1设A为诺特分次代数,I为A的余有限的双边理想.设B为式子(1)定义的矩阵代数.则有Abel范畴等价qgrA≅qgrB.

证明由引理2,B是右诺特分次代数.故qgrB也是Abel范畴.令M=Be,则M是分次B-A-双模,并且作为左B-模或者右A-模都是有限生成的.类似地,令N=eB,则N是分次A-B-双模,且作为左A-模或者右B-模都是有限生成的.于是可以构造如下函子

F=-⊗BM:grB→grA,G=-⊗AN:grA→grB.

由于eBe≅A,对于任意分次A-模X,

FG(X)=X⊗AN⊗BM=X⊗eBeeB⊗BBe=X⊗eBeeBe≅X.

(2)

故FG自然等价于恒等函子.

由于M是投射B-模,故函子F是正合函子,并且F将有限维模对应到有限维模.因此,F诱导了商范畴之间的函子

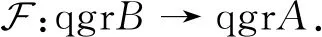
另一方面,由于N是有限生成左A-模,则对于任意有限维右A-模Y,Y⊗AN必定也是有限维的.设f:Y→Y′为分次右A-模同态,且kerf和cokerf都是有限维的.由张量函子的右正合性,态射f⊗AN的余核也是有限维的.由于kerf⊗AN是有限维的,且态射f⊗AN的核是右B-模kerf⊗AN的同态像,故kerf⊗AN也是有限维的.于是由商范畴的泛性质,G诱导了如下商范畴之间的函子[13]

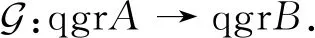
记π:grB→qgrB为投影函子(grA到商范畴qgrA的投影函子也记作π).以下证明类似于[14,Lemma 2.9].

考察正合序列

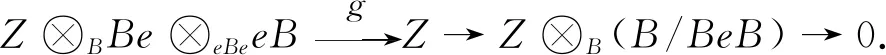
由于B/BeB是有限维的,Z⊗B(B/BeB)也是有限维的.

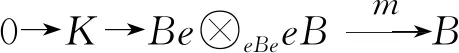
证明由于A是局部有限的,A≥n是余有限的双边理想.由命题1,即可得到结论.证毕.

3 主要结论

设A是右诺特分次代数,在这一节中,我们将考察n-阶矩阵代数,并且将上一节的结论推广至n-阶矩阵情况.构造矩阵代数如下

(3)

其中,Iij(1≤i

引理3设A为右诺特分次代数,B为如上定义的矩阵代数.则B也是右诺特分次代数.

证明由于A是右诺特分次代数,双理想Iij都是有限生成的右A-模.类似于引理2的证明过程,可以将A中元素对应到B的主对角线元素,从而将A看作是B的子代数.由此,B是一个分次右A-模,并且作为右A-模,B是一些有限生成的右A-模的直和,故B作为右A-模是有限生成的,因此B是右诺特分次代数.证毕.

有上述引理,若A是右诺特分次代数,则B也是右诺特分次代数,故商范畴qgrB是Abel范畴.

定理1设A是局部有限的右诺特分次代数,设B为形如等式(3)中构造的矩阵代数.

(ii)若A的右整体维数是有限的,且对于所有i,j都有Iij=A≥1,则B的右整体维数也是有限的.

证明(i) 对矩阵代数B的阶数n作数学归纳.当n=2时,即为命题1情况.

现假设结论(i)对于小于n时的情况都成立.将B写作如下形式

其中I=(I12…,I1n),J=(A,…,A)T,

由归纳假设,有Abel范畴等价 qgrA≅qgrC.

(4)

由结论(i)的条件,I1是余有限的,故B/BeB是有限维的.再由命题1的证明可得Abel范畴等价qgrB≅qgrC.结合式子(4),得到Abel范畴等价qgrB≅qgrA.

(ii) 由于A的右整体维数是有限的,则代数A0的右整体维数必定也是有限的.事实上,任意一个右A0-单模S都可以看成是一个分次右A-模.假设A的右整体维数为d,设0→Pd→…→P1→P0→S→0是S作为分次右A-模的投射分解.由于A是非负分次代数,则前述投射分解的0次部分构成了S作为右A0-模的投射分解.故A0的右整体维数必定不大于d.又由于所有双边理想都有Iij=A≥1(1≤i

例1设A=K[x1…,xn]为多项式代数,则A是诺特代数且右(或左)整体维数为d.令

其中n≥2.则由定理1以及文献 [15],B的整体维数等于d,但C的右整体维数为无限.

注记1 满足定理1 (iii)条件的矩阵代数B都具有无限整体维数,假如分次代数A的右整体维数是有限的,则Abel范畴等价qgrA≅qgrB在一定意义上说明分次代数A是分次代数B的非交换奇点解消[5].

4 Koszul性质

这一节将证明一类特殊的矩阵代数是Koszul代数,从而给出构造非连通Koszul代数的方法.

设A=K⊕A1⊕A2⊕…为连通Koszul代数,设平凡模KA有如下极小投射分解:

(5)

其中,对于n≥1,Vn是有限维分次向量空间,并且Vn的非零元素都集中于n次.对于任意n≥1,定义线性映射

φn:Vn→Vn-1⊗A1

为φn=dn|Vn,这里V0=K.于是对于任意v∈Vn,a∈A有dn(v⊗a)=φn(v)a.

都是投射右B-模.

其中,δ0为自然投影映射,

其中,∂0为自然投影映射,

引理4上述构造的序列(7)和(8)分别是右B-模e1B0和e2B0的投射分解.

证明只要证明序列(7)是正合的,序列(8)的正合性类似.

(9)

其中,fn(v⊗a,u⊗b)=(φn(v)a,φn(u)a),∀v,u∈V,a∈A.

(10)

由于A是Koszul代数,序列(9)是正合的,故序列(10)正合,进而序列(7)是正合的.证毕.

证明由引理4,得到e1B0与e2B0的右B-模投射分解.注意到e1B0⊕e2B0=B0,并且引理4中构造的投射模分解的第n个投射模是由n次元素生成的(n≥0),因此,B是Koszul代数.