考虑载货量的危险品运输车辆路径优化

张圣忠，陈婷婷，孙荣庭，白 雪，高 超

(长安大学 经济与管理学院，陕西 西安 710064)

随着工业化进程的加速，危险品运输量在逐年上升[1]。据交通部统计，2017年国内危险品运量达到11亿t，且在以每年10%的速度增长，其中道路运输是危险品运输的主要手段，占95%以上。不同于普通物品，危险品在运输过程中容易出现侧翻、碰撞、泄漏、燃烧、爆炸、中毒等现象，且一旦发生事故就可能造成人身伤亡、财产损毁和环境污染等严重后果[2]。这不仅会造成了运输损失，还会对沿途人民的生命和周边环境造成严重威胁。因此，在保障安全的前提下对危险品运输车辆路径进行合理的优化就显得十分重要。

危险品运输车辆路径优化问题(vehicle routing problem for hazardous, HVRP)一般是将危险品运输特性和VRP问题结合起来，考虑容量限制、总运输时间限制和时间窗口限制等约束,以总运输成本最小化和总风险最小化为目标。KARA等[3]首次提出一种考虑风险和成本的双目标优化模型, 使用库恩-塔克条件和互补松弛条件将其转换为单目标模型,并对模型进行求解。ZOGRAFOS等[4]提出了危险品运输VRP的双目标模型，使用线性加权方法将所提出的双目标模型转换为单目标模型，并对其进行求解。MENG等[5]提出了在有限的运行时间段、服务时间和节点等待时间窗约束下的车辆路径模型，并提出了求解的动态规划方法。PRADHANANGA等[6]提出了一种具有时间窗约束的双目标VRP，并提出了一种元启发式算法，以提供一组帕累托较优解。ERKUT等[7]将危险品网络设计问题归结为树选择问题，采用树状网对双层规划模型进行分析，并用启发式算法求解模型。辛春林等[8]针对HVRP问题给出了详细的综述,并提出了求解单目标和多目标问题的智能算法。

危险货物运输风险的度量也是HVRP问题中的重要因素。在以往的研究中，学者们一般利用“传统风险模型”[9]来衡量危险品运输过程中的风险，该模型通常以随机分布来表示事故发生概率，以距事故现场特定距离内受影响的居民人数[10]来表示事故后果。后来也有学者考虑到了运输车辆的载货量对风险带来的影响，如PRADHANANGA等[11]使用危险品运输车辆的额定载货量和人口暴露数来衡量危险品的运输风险。不过大多数研究者仍采用人口暴露数来衡量运输风险，目前仅有少量研究考虑到了载货量动态变化对风险的影响，如袁文燕等[12]提出了随载货量线性变化的风险测度方法，其所建模型以最小运输距离和最小风险为目标，且未考虑服务时间窗的约束。综上所述，目前针对危险品运输路径规划问题的研究还不够充分，与实际危险品运输情景仍存在较大差距。为了进一步贴近现实情况，笔者考虑了HVRP问题中载货量动态变化对运输风险的影响，同时考虑配送时间窗约束，以最小化危险品运输的车辆数、运输总距离和运输风险为目标函数，建立了考虑载货量的危险品运输车辆路径问题模型，决策危险品运输车辆数和车辆服务路径。

在求解HVRP优化问题方面，常用传统的精确算法往往由于问题复杂而造成计算量巨大，为此有学者提出分布估计算法求解多目标问题[13-14]，可以提高模型的鲁棒性，该算法可以有效应用于车辆路径优化问题的求解[15-16]。因此，笔者设计一种基于概率模型的多目标进化算法对提出的HVRP问题进行求解，先采用NSGA2算法的非支配排序方法来获取进化群体，再通过概率模型进行随机采样计算每个可行解的目标值和对应的路线。针对考虑载货量的危险品运输车辆路径优化问题，通过概率模型来描述实际载货量和风险之间的线性关系，并在选择机制中融入NSGA2算法的概念，基于群体的宏观进化方式，使其可以利用HVRP问题的结构信息来产生更好的个体，扩大多目标进化算法的搜索范围，保证算法解的可行性以及求得完整的Pareto前沿。

基于以上考虑，在采用实际载货量建立新风险度量模型的基础上，笔者研究了一种以最小化运输距离、车辆数和运输风险作为优化目标且考虑服务时间窗约束的多目标路径优化问题，建立数学模型，提出一种基于概率模型的多目标进化算法对问题进行求解。并通过对3种按道路网络节点形成的不同分布进行算例仿真，以验证模型与算法的有效性。

1 考虑载货量的危险品运输车辆路径问题建模

1.1 问题描述

研究问题可以描述为：在危险品道路运输网络中有一个配送中心、多个客户需求点和若干危险品运输车辆。在不超载的情况下，配送中心根据每个客户节点的需求量在配送时间要求内进行分配，直至满足每个客户需求，一辆车可为多个客户需求点进行配送并确定配送车辆的数目。从配送中心同时派发多个危险品运输车辆对各自分配的需求点进行服务，服务完成后车辆必须返回到配送中心。主要假设有：①配送中心拥有足够的库存满足辖区内各个需求点需求；②各需求节点的需求量和时间窗要求可提前获知且需求不可拆分；③配送中心及需求点之间的行驶距离、事故概率、暴露人口数已知；④所有配送车辆额定载货量相同。

已知危险品道路运输网络系统G=(N,A)，其中N={0,1,2,…,n}代表危险品配送中心0和该配送中心所有客户需求节点i的集合，A代表连接需求节点及配送中心的所有道路的集合。各节点之间的距离为dij,每个需求节点i的需求量及配送时间窗要求分别为qi和[ETi,LTi],k辆具有容量W的配送车辆从配送中心0出发，按照配送路线依次完成相应需求节点的配送，最终返回到配送中心。

1.2 参数及变量定义

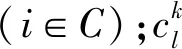
1.3 风险度量模型

在HVRP问题中，运输车辆从仓库出发依次访问若干个需求点后返回仓库，配送车辆上危险品载重量的不断变化与车辆的访问路径密切相关。

传统的风险度量模型以Rij=pijφij来度量边(i,j)上的道路风险，其中pij，φij分别为车辆在路径(i,j)上发生事故的概率及事故导致的后果(通常用人口暴露数来表示)，不考虑载货量与事故影响后果的关系，因此无法准确衡量路径风险。基于以上考虑，笔者假定风险影响后果与危险品的载货量存在线性关系，于是有：

(1)

车辆k的第m段配送路径上的载货量为：

(2)

则车辆k的第m段配送路径上的风险为：

(3)

那么车辆k配送路径上的风险为：

(4)

1.4 模型建立

该问题的优化的目标为：

(5)

(6)

(7)

该问题的可行解必须满足的约束条件有：

(8)

(9)

(10)

(11)

(12)

(13)

Tjk=Tik+tijxijk,ETj≤Tjk≤LTj,

∀i∈N,∀j∈C,∀k∈K

(14)

xijk∈{0,1},∀i,j∈N,∀k∈K

(15)

yik∈{0,1},∀i∈C,∀k∈K

(16)

式中：目标函数(5)表示最小化运输总距离；目标函数(6)表示最小化车辆数；目标函数(7)表示最小化风险；约束条件(8)表示每个需求点只有一辆车为其服务；约束条件(9)表示每辆车出发时最多只能访问一个客户；约束条件(10)表示每辆车到达时最多只能配送一个客户；约束条件(11)表示车辆到达某客户节点完成配送后必须从此节点出发；约束条件(12)表示确保每个客户被访问一次，并返回到配送中心；约束条件(13)表示车辆载货量约束；约束条件(14)表示配送时间窗约束，要求车辆必须在时间窗内开始配送；约束条件(15)和(16)表示决策变量的取值范围。

2 算法设计

相关研究解决HVRP问题通常用遗传算法进行求解[17]，KALYANMOY等[18]提出基于拥挤距离的分布性方法的快速非支配排序遗传算法NSGA2,但是NSGA2存在交叉、变异等遗传操作对问题结构破坏的设计缺陷，且无法考虑到变量之间的相关依赖关系，从而通过引入概率模型捕获问题中的结构关系，降低破坏程度，并在求解效率和解的质量上有较大的优势。基于此，笔者提出一种基于概率模型的多目标进化算法对HVRP问题进行求解，该算法通过NSGA2的非支配排序方法进行种群选择和构造非支配解集，将参与进化的个体进行构建概率模型，并选取轮盘赌策略对概率矩阵进行更新、归一化、随机采样等操作来求解多目标优化模型。

2.1 初始解

对模型采用自然数定长编码的方式进行求解，解码得到的路径由危险品车辆运输的配送中心和需求点编号组成。例如1-12-8-10-21-1-20-11-2-1-13-4-25-1-3-16-7-1-24-5-14-1-22-23-1-6-9-18-1-15-17-19-1，该路径的数字1为配送中心，其他数字表示车辆对需求点的配送顺序，其中1-12-8-10-21-1表示同一辆车对不同需求点进行配送并返回到配送中心。通过编码产生初始解时，首先采用NSGA2算法获取种群的优势个体，既可得到运输方案的可行解，又提高了算法的鲁棒性；其次在其个体领域内获取部分解；最后与产生的其他解一起随机生成初始解。

2.2 非支配集的构造

通过非支配排序的方法构造问题的非支配解集，根据解之间的支配关系构造，从配送中心出发，为了保持种群在解空间的分布性和多样性，将个体的拥挤距离作为种群中个体之间的比较准则，使得准Pareto域中的非支配解能均匀扩展到整个域，对可行解进行快速非支配排序并计算拥挤距离来进行比较操作，再根据相邻解的拥挤距离大小选择精英个体直接进入下一代种群参与进化。个体聚集密度的计算式为[19]：

(17)

式中：P[i]distance表示个体i的聚集密度距离；P[i]·m表示个体i在子目标m上的函数值；fk表示有k个子目标；r表示种群子目标的个数。

2.3 概率矩阵

根据参与进化的个体进行构建概率模型，在危险品运输车辆的装载不为空或者当前时刻不在配送时间窗范围内的情况下，采用轮盘赌策略对选取的精英个体进行采样，选取第m段路径配送首节点的车辆，对配送车辆k+1进行迭加，再计算节点ci为某条路径首节点的概率qr，从中选取适应度较高的个体，并统计相同车辆配送的节点ci和cj在同一路径上相邻的概率pr，计算方法如式(18)和式(19)所示。

(18)

(19)

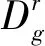
2.4 算法流程

算法具体流程：①参数初始化。构造初始解并初始化非支配解集，令初始迭代次数gen=1，最大遗传代数maxgen=100。②对目标进行解的构造，构造N个解；根据所有客户的需求量，通过概率模型采用轮盘赌策略随机选择下一个被访问的需求点j，直至配送车辆载货量为0并记录该配送路径，并返回仓库；进行下一路径的选取。③进行非支配解的筛选，计算最优的非支配解集第m段路径的目标函数值并更新进化，在多次求得的非支配解集中再次求非支配解集,以达到较优解集。④重复步骤②，直至gen=maxgen。基于概率模型的多目标进化算法流程如图1所示。

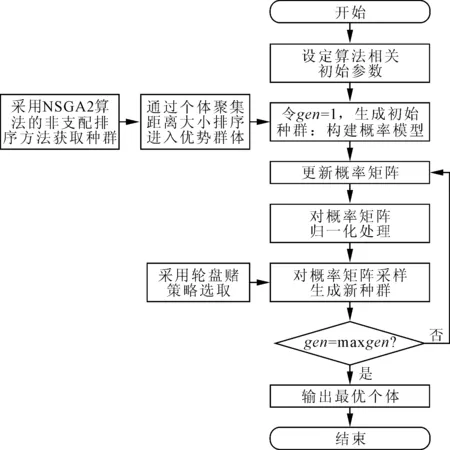
图1 基于概率模型的多目标进化算法流程图

3 仿真结果与分析

笔者通过数值仿真实验来检验目标模型的效果。实验设置3组相同的数据规模和按需求点的地理位置或时间窗的3组不同的分布数据，均考虑24个顾客需求点和1个仓库，SOLOMON[20]算例为VRP领域公认的经典算例，因此笔者也选取该算例进行研究。道路系统中的事故概率和人口密度信息随机生成。算法的参数设置个体数为200个，最大迭代次数为100次，优势种群数为40个，采用Matlab编程实现该算法。

3.1 算例对比分析

采用SOLOMON算例按网络节点的地理位置或时间窗形成聚类分布、均匀分布和介于两者之间3组不同分布的算例，分别为R101、RC101和C101数据。R101的车辆集中分布在运输距离680～780 km之间，而C101的车辆数在各个运输距离段呈现平均分布，且车辆数较少，RC101的车辆数在各个运输距离段也呈现平均分布，但在每一个时间段内的车辆数比C101集中。选取3组不同分布的顾客坐标、需求、时间窗和服务时间的信息作为基本算例，按车辆数进行分类后各自分布的Pareto解如图2所示。

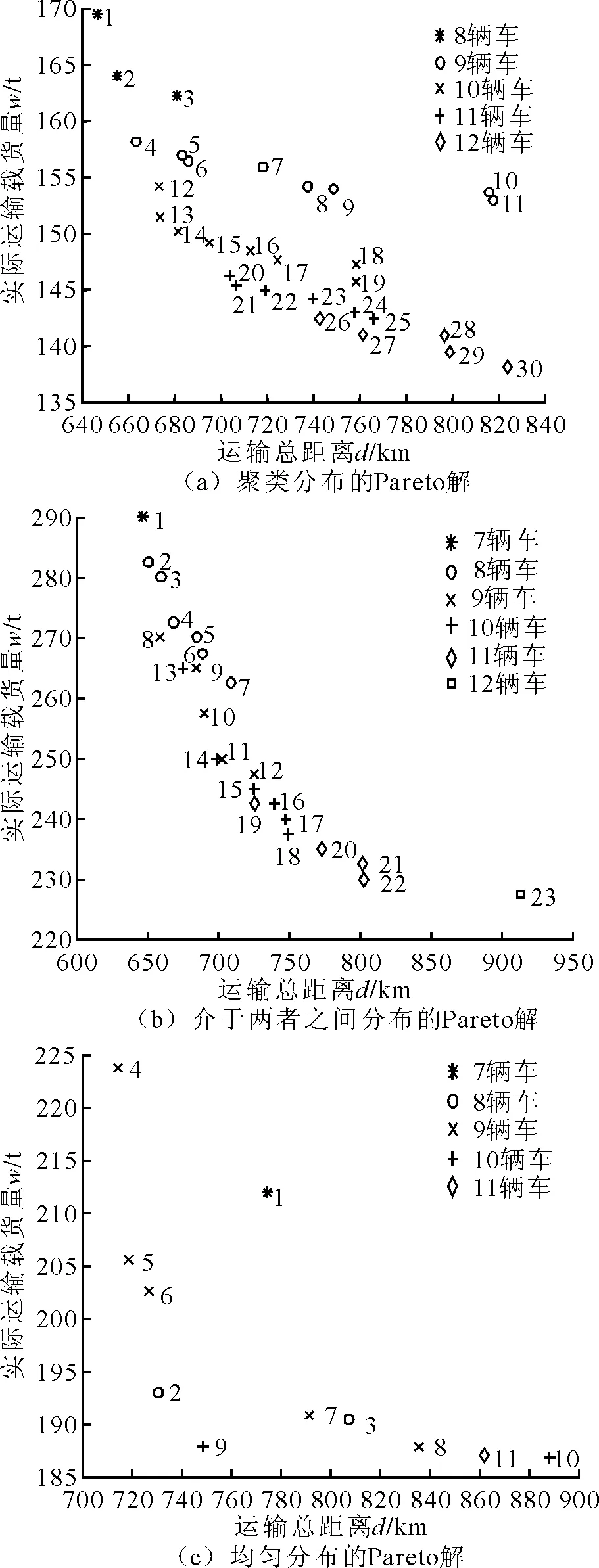
图2 按网络节点位置分布的Pareto解

不同分布生成的Pareto解的信息如表1所示。结合图2和表1可知：①当顾客点相同时，考虑载货量的聚类分布生成30个Pareto解，均匀分布生成11个Pareto解，在聚类与均匀之间的分布生成23个解，不考虑载货量的Pareto解只有2个，这表明基于概率模型的多目标进化算法在考虑载货量的情况下可以求得更多的Pareto解，对运输过程中的动态变化较为敏感。②按网络节点的地理位置形成的均匀分布生成的解空间相较而言更为分散，这表明基于概率模型的多目标进化算法可以对不同分布的个体聚类距离进行计算，根据顾客地理位置分布的分散程度，其对解的搜索范围加大，导致运行时间增加。

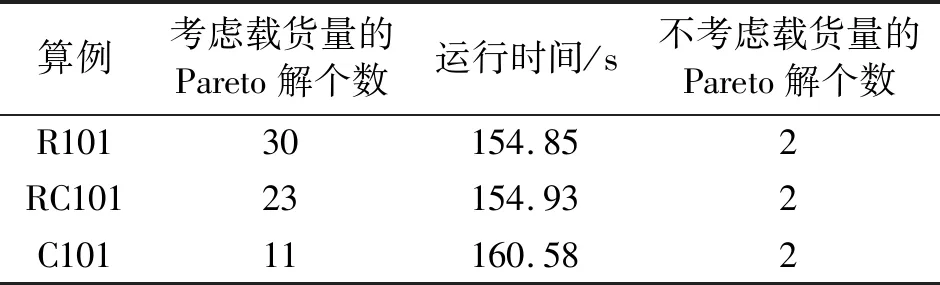
表1 不同分布生成的Pareto解的信息

3.2 聚类分布的算例分析

以25个网络节点位置形成的聚类分布为例，对比分析两种不同风险度量方式(即考虑载货量和不考虑载货量)下3个目标的Pareto解集风险值，如表2所示。

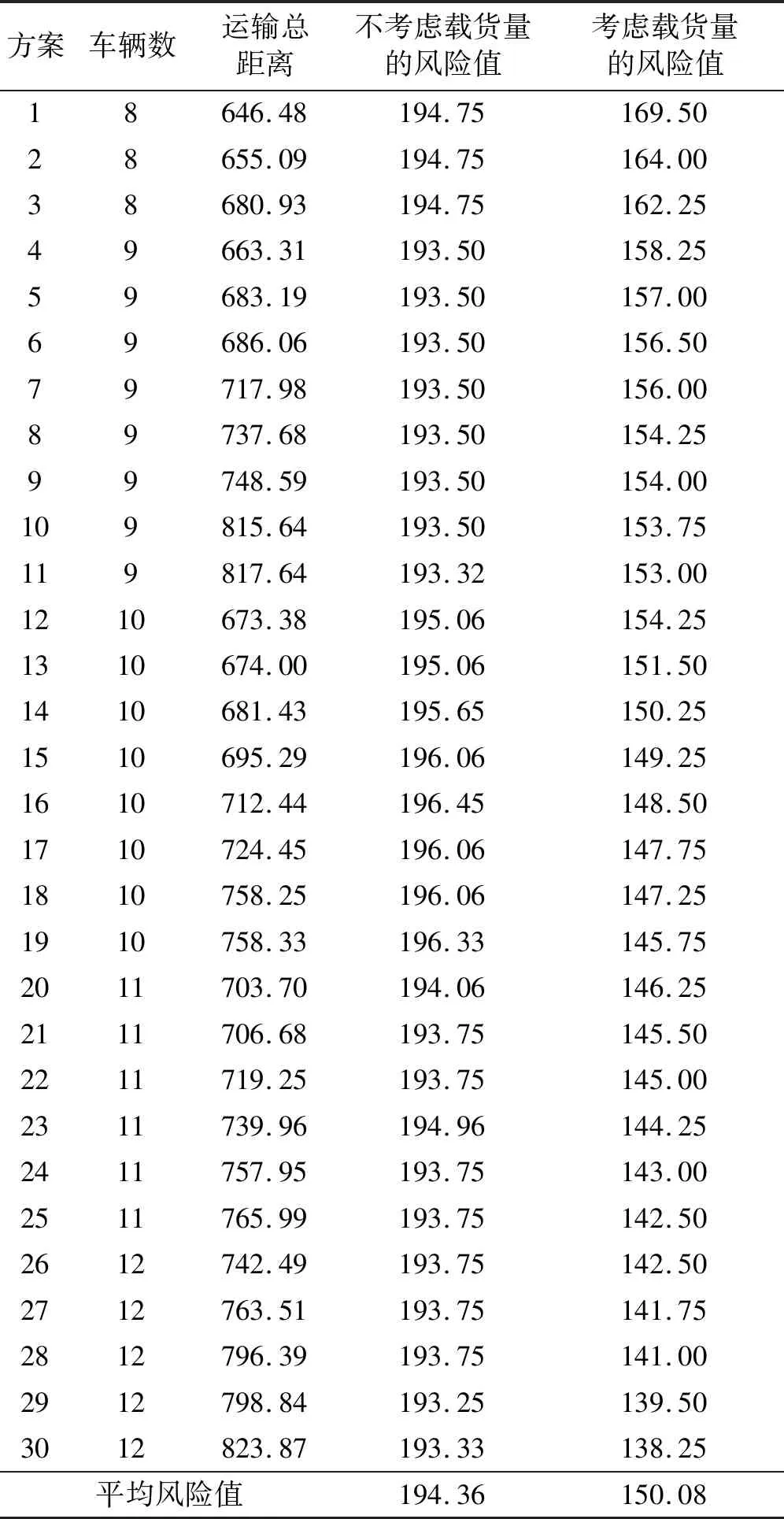
表2 不同风险度量方式下的Pareto解

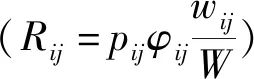
对考虑载货量的风险度量方式进行细节描述，通过R101算例进行仿真计算获得一组Pareto解，记录了对应的3个目标值和路线，如表3所示。

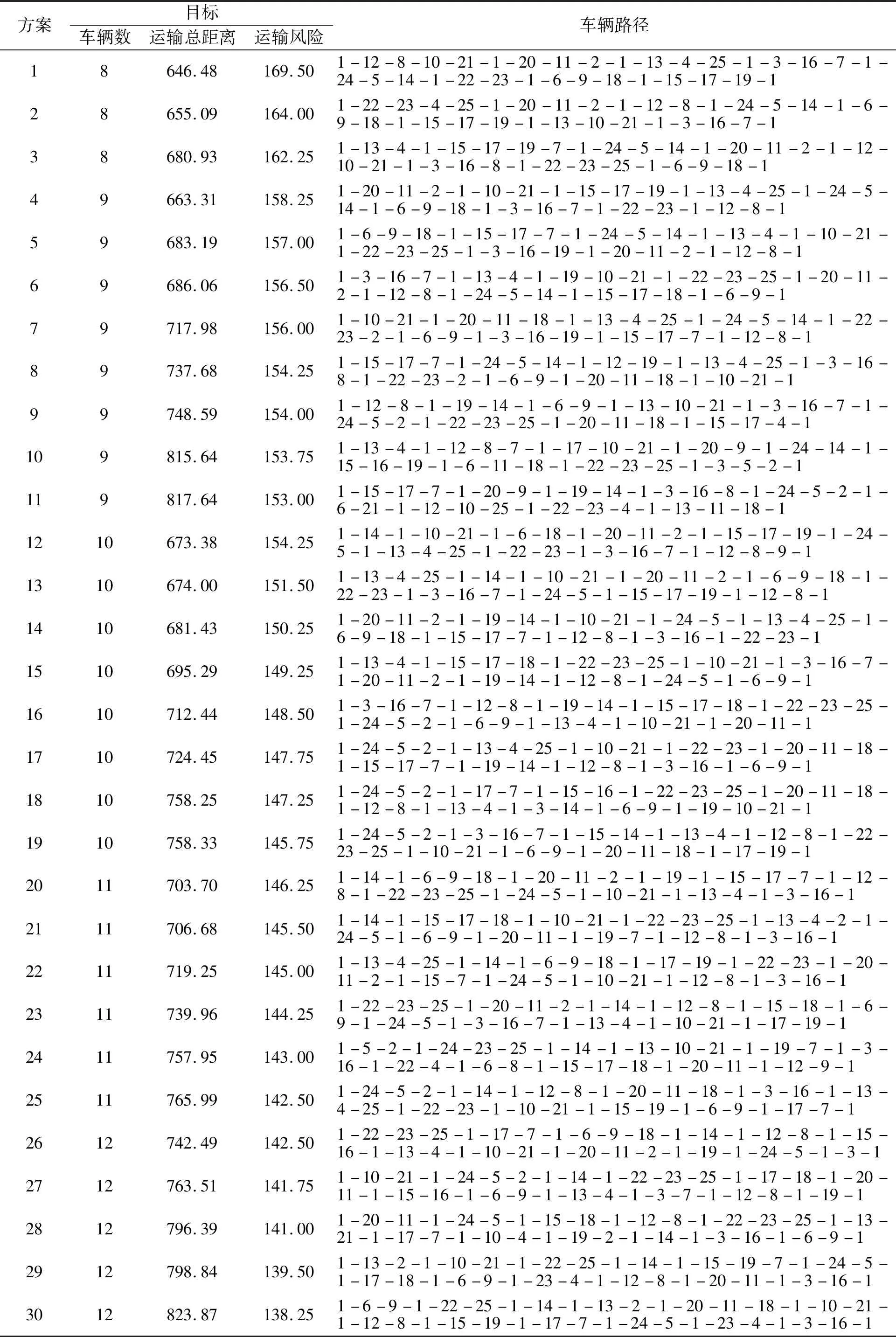
表3 R101算例的Pareto解

从表3可以看出，随着方案中车辆数目的增加，运输风险不断降低，但是运输距离呈上升趋势。这是因为在整体需求不变的情况下，车辆数增加会导致每辆车的配送节点减少，分配到每辆车上的危险品数量减少，完成配送任务至空车的速度加快，因此总风险下降；但是车辆数增加会降低单车配送效率，因此总距离上升。R101数据中顾客需求点位置坐标所形成70×80区域的运输轨迹路线如图3所示，如果决策者偏向于成本最低，可以选择方案1的轨迹路线；如果决策者偏向于风险最低，可以选择方案30的轨迹路线。

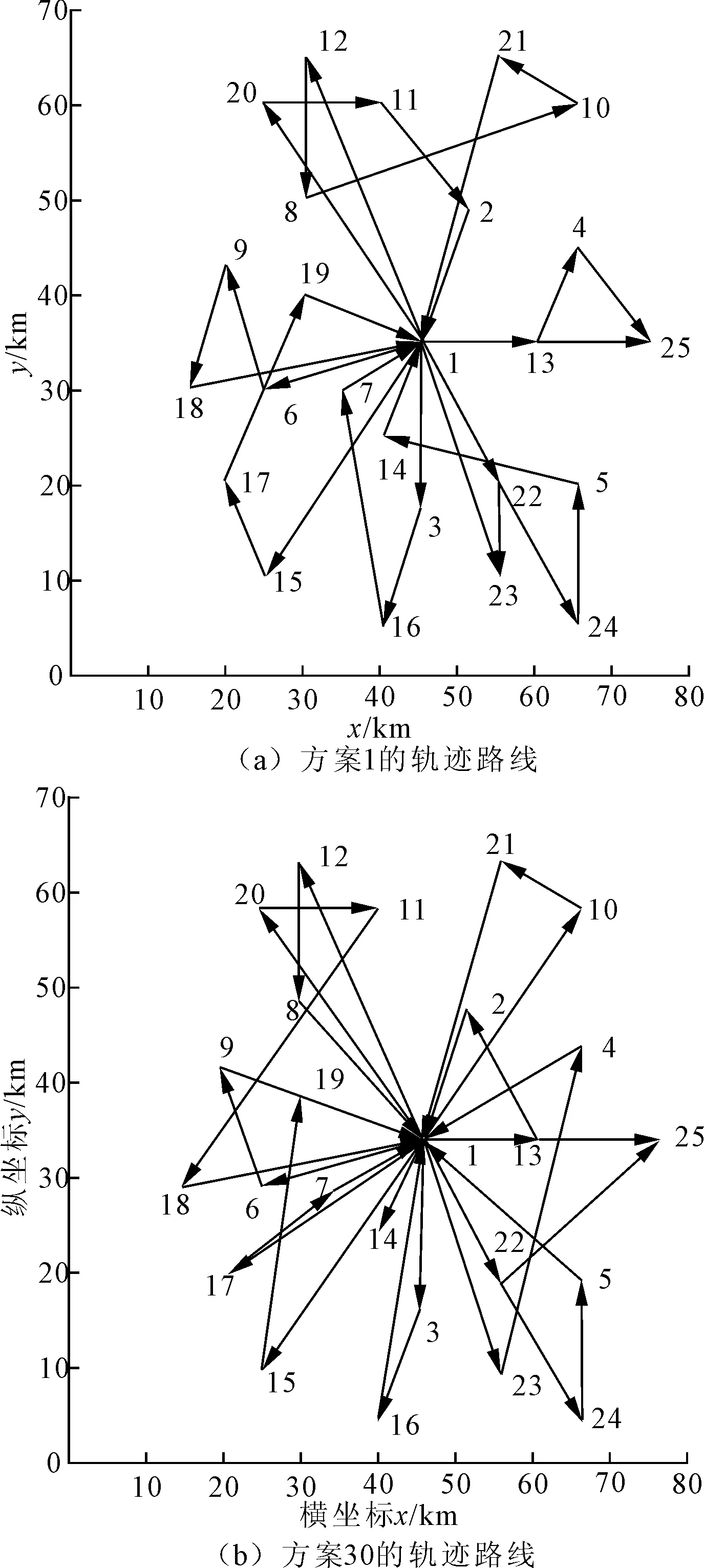
图3 非支配解的轨迹路线

4 结论

(1)考虑载货量和服务时间窗的危险品车辆运输路径问题，建立以最小化车辆数、运输总距离及运输风险为目标的HVRP多目标优化模型，并设计了一种基于概率模型的多目标进化算法来求解问题。模型引入了配送时间窗的约束，并将车辆数作为路径优化中考虑运输成本的目标之一，从而决策者可以按车辆数目从Pareto解集中选择满意的危险品运输路径，且能够为决策者提供更多的路径选择。

(2)通过数值分析发现，概率模型对变量之间的关系进行估计的进化算法能够获得多目标问题的有效Pareto解。通过对顾客的地理位置或时间窗不同分布的算例求解，验证了模型的有效性，计算结果和运行时间也表明了基于概率模型的多目标进化算法对解空间有着较强的搜索能力。

(3)考虑载货量时，3种分布情况下得到的平均Pareto解集个数为21个；但不考虑载货量时，3种分布的Pareto解仅有2个。通过对不同风险度量模型进行计算发现，在不考虑载货量的风险度量方式下，Pareto解集的风险值分布较单一，且同比平均风险值，其风险值波动范围不超过2%；在考虑载货量的风险度量方式下，Pareto解集的风险值分布更加多样，其风险值在8.5%～12.9%范围内波动。因此，考虑载货量的风险度量方式可以提供风险多样化的决策方案，以满足不同决策者的风险偏好。

(4)笔者在设计风险模型时，考虑到对模型复杂程度的影响，并没有考虑危险品属性、路况、天气等多种因素对于危险品运输风险的相关性，可以在未来进一步深入研究。