考虑处理量优化的自提点选址多目标规划研究

黄 露，纪延光

(1.中国矿业大学 管理学院，江苏 徐州 221116；2.江苏海洋大学 商学院，江苏 连云港 222005)

随着我国电子商务的快速发展，快递量呈现迅速增长的趋势。国家邮政局数据显示，2019年全国快递业务量高达630亿件，同比增长24%，连续六年稳居世界第一。阿里研究报告显示，高校网购人群密度大，在全国网购用户中排名第三，快递量占全国总量的6%。为应对快递需求的不断增加，进一步降低配送成本，快递企业正在积极推广自提点建设。自提点具有灵活性、便利性、投资费用低等特点，越来越被企业和顾客所接受[1]。然而，随着消费体验逐步升级，自提点的服务能力已经不能满足顾客不断增长的服务需求[2]，这时快递企业不得不考虑优化自提点的处理量，科学规划自提点选址，以期提高自提点的运作效率和服务质量，进而有效解决成本和自提点服务能力之间的矛盾。

与其他选址问题不同，自提点选址问题直接面对顾客，是一个复杂的决策问题，涉及到企业、顾客等多个参与人员，在优化自提点选址过程中，要考虑多个目标才能符合实际情况。已有研究主要从理论模型和求解算法等方面对自提点选址进行了研究，如周翔等[3]通过聚类算法分析自提点的预选址数量等信息，建立自提点覆盖选址模型，设计网格密度聚类算法求解模型。VAHDANI等[4]考虑不确定条件下应急物流的两阶段多目标选址模型，运用元启发式算法求解。杨朋珏等[5]采用遗传算法求解带有客户满意度和配送效率优化的选址模型。陈义友等[6-8]基于顾客选择的选址问题，构建了以企业成本最小、需求量最大、顾客价值最大为目标的模型，提出双层迭代法进行求解，结果表明顾客选择行为影响自提点的运作效率和资源优化配置。陶志文等[9]建立了带有物流成本、顾客服务水平、碳排放等多因素的多目标模型，并用粒子群算法进行求解。SILVA等[10-11]分别考虑了设施的容量限制、个数约束、服务时间等因素，给出以等待时间最小为目标和需求量最大为目标的模型。韩珣等[12]进一步考虑顾客拥塞成本的自提点容量优化研究，建立了自提点容量优化选址模型，并分析影响选址变动的因素，研究结果对于企业布局自提点具有指导作用。

上述关于自提点选址的研究趋向于多个主体在考虑不同约束条件下的多目标模型及其求解算法，丰富了模型和算法的种类。然而，随着消费需求的不断升级，上述研究虽考虑了设施容量、服务时间等因素，但依然不能满足顾客的使用需求。为此，笔者引入处理量规模约束，构建基于自提点处理量优化的多目标选址模型，以优化自提量、降低成本为目标，试图权衡自提量和成本之间的博弈问题。在此基础上，通过连云港某自提网点处理量优化案例展开分析，使优化后的自提网络能够满足顾客的服务需求。

1 模型构建

1.1 问题描述

自提点选址问题，即为企业选址和需求点分配问题。企业考虑需求点位置和需求量后，在满足费用等约束条件下，从备选自提点中选择若干最优的自提点，合理规划需求点的分配，使得选址成本最小和顾客自提量最大。因此自提点选址要解决的问题是：企业对自提点选址问题进行决策，使得顾客最优分配策略下的自提总量最大和选址成本最小。

模型假设主要有：①顾客实际需求是动态的，以顾客日平均需求量为基础进行研究；②每个顾客只有一个自提点提供服务；③顾客以自提点提供的效用为选择依据，用自提点覆盖度表示效用函数；④自提点包裹处理成本存在规模效应，用阶梯型函数表达。

1.2 符号定义

在选址网络G(V,S)中，Vi为顾客点集合，Vi={i,i∈V}；Sj为候选自提点集合,Sj={j,j∈S}；B为预期费用；Mj为自提点中转量，且在自提点容量范围内；yj为0-1决策变量,yj=1表示选中候选点j作为自提点，否则yj=0；fj为自提点j的运营费用；Ckj为中转中心k到自提点j的单位运输费用；Di为需求点i平均每天的自提量；xij为0-1决策变量，xij=1表示顾客i选择自提点j服务，否则xij=0；dij为第j个自提点到客户点i的最短距离；C(dij)为覆盖度函数；R1为自提点覆盖最大临界距离；R2为自提点覆盖最小临界距离。

1.3 模型建立

结合企业和需求点之间的目标决策关系，构建自提点选址问题模型：

(1)

(2)

s.t.

(3)

(4)

(5)

(6)

xij≤yj,∀i∈V,∀j∈S

(7)

yj∈{0,1},∀j∈S

(8)

xij∈{0,1},∀i∈V,∀j∈S

(9)

(10)

(11)

式(1)表示最大化自提总量。式(2)表示最小化选址成本，包括从中转中心到自提点的运输成本、自提点的物资处理成本和运营成本。式(3)表示自提点日处理量约束。式(4)表示自提点运营成本约束。式(5)表示自提点建设个数大于等于1。式(6)表示每个需求点有且只有一个自提点服务。式(7)～式(9)为相关决策变量约束。式(10)为覆盖度函数的表达式。由于顾客具有理性行为，其选择意愿会受自提点距离的影响[13]，为表达这种现象，因此采用顾客到自提点的距离效用表示自提点覆盖度C(dij)，且覆盖度随着取货距离的增加而降低，呈分段线性关系。式(11)为自提点的日处理成本的表达式，由于存在规模效应[14]，随着自提点处理量的增长，处理成本不是线性函数关系，而是用分段函数描述。其中，D=Dixij表示自提点j的包裹处理量；Fj(D)是关于包裹处理量D的凹函数，且∂ln[(D-D2)a]/∂D>0，∂ln[(D-D2)a]/∂D2<0,表达包裹处理过程中的“规模效应”；D2为自提点临界参数；Ej1为系数；a为自提点规模效应系数，a∈(0,1)。

2 模型求解

多目标规划模型的各目标相互矛盾，很难同时得到最优，但存在Pareto最优解集。对于多目标规划模型的求解，可直接用粒子群算法，但在求解模型的过程中存在解的多样性较差、易陷入局部最优等弊端[15]。而NSGA-Ⅱ算法[16]是求解多目标模型应用最为广泛、有效的算法，具有全局最优解搜索能力。NSGA-Ⅱ算法引入精英策略、非支配排序，能够快速找到具有良好收敛性和保持多样性的Pareto最优解，使求出的解具有更好的效果。因此，笔者将NSGA-Ⅱ算法用于自提点选址问题的求解，具体流程如下：

(1)参数初始化。为模型参数和算法参数赋值，生成选址方案的初始种群Y(N)，设进化代数N。决策变量(yj,xij)为种群个体的编码方式。

(2)计算适应度值和非支配排序。基于目标函数值z1、z2的适应度值，对染色体非支配排序，所有的解都划分到相应等级前端，同时计算同一前端个体拥挤距离；选择等级小和拥挤度大的个体组成种群Y1。

(3)对种群进行遗传算法操作，产生新的种群NJ；父代种群Y(N)和子代种群NJ合并形成新的种群RJ。然后对种群RJ进行非支排序和拥挤度计算，重复上述步骤，直到满足迭代条件为止。

(4)算法终止条件。判断N是否达到最大进化代数，若是，则停止迭代，根据实际情况选择最优方案；否则，令N=N+1，生成新的种群Y(N)，返回步骤(2)继续迭代。

3 案例分析

以连云港某高校自提点网络为案例，选取平均每天的需求量和自提量作为研究数据，对自提点选址模型进行求解，得出成本最低、顾客效用最大的选址方案，并与某高校的自提点现状进行对比，证明模型和算法的有效性。自提点到需求点的距离根据百度地图定位出两地点的经纬度，计算出两地点之间的最短距离。根据实地调查得出需求区域的人均包裹需求量和各需求点的人口总量，运用公式“需求点的日均包裹总需求量=需求点人口量×人均包裹需求量”，得出各需求点的日均包裹需求量。根据连云港的平均工资水平和消费水平设置自提点的参数，车辆购买费用为8万元，员工工资为3 000～4 000元/月，自提点配置面积为70～80 m2，每天租金为3.5～5.0元/m2，以此计算出自提点固定成本为400～1 000元/天(包括工资、水电、设备等)。中转中心到自提点的单位运输费用为3元/km，自提点最大中转量为2 500个/天，自提点处理能力为600～2 500个/天，自提点最小覆盖距离为300 m，最大覆盖距离为500 m。自提点A(A1～A7)到需求点Q(Q1～Q7)的数据信息如表1所示。

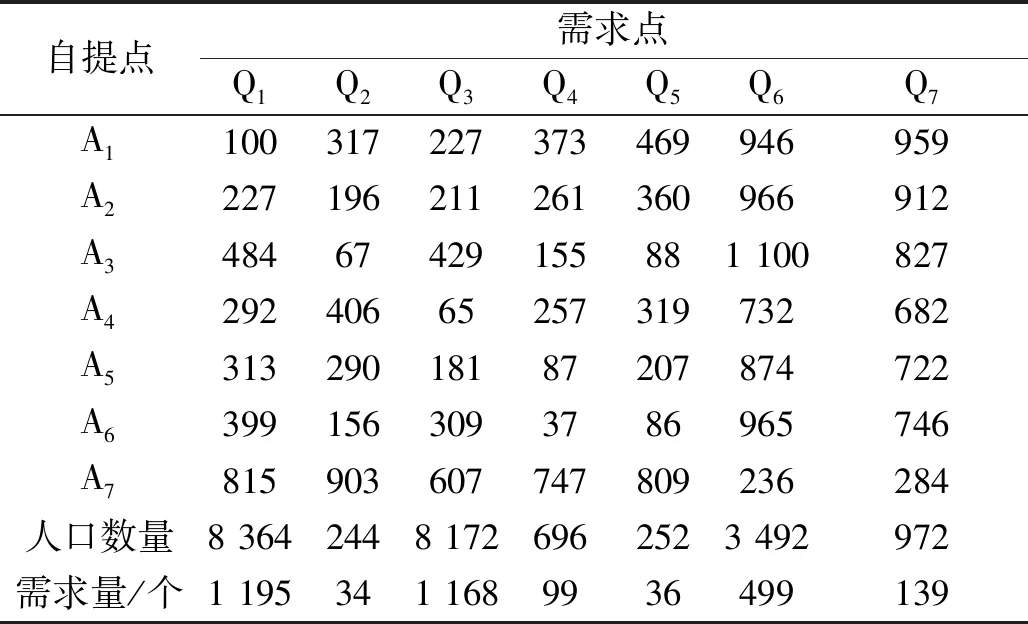
表1 备选自提点到需求点的相关信息

3.1 求解结果及分析

为了验证模型算法的有效性，分别对仅考虑自提量的单一目标模型、仅自提点选址成本的单一目标模型和综合考虑自提量和成本两个因素的双目标模型进行了求解，结果如表2所示。

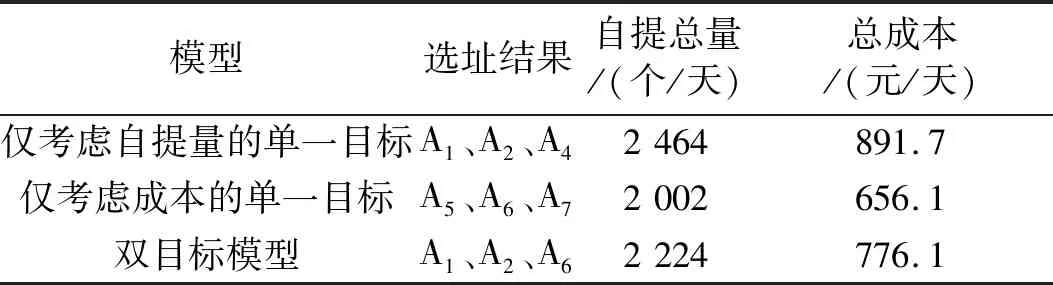
表2 不同模型下的自提量和成本的比较

从表2可以看出，综合考虑自提量和成本的选址方案比仅考虑成本的方案物流成本增加了18.29%，自提量增加了11.09%；比仅考虑自提量的方案自提量减少了9.74%，选址成本减少了12.96%。这表明双目标模型在选址过程中考虑了企业和顾客两个因素，平衡了自提量和成本之间的关系，具有较好的综合优势。同时，双目标模型比仅考虑自提量的单目标模型成本减少了115.6元，更符合企业降低成本的实际需要。

利用上述模型和算法计算现有自提模式的成本，通过多次模拟得到最优的参数设置：种群规模NP=100，最优前端个体系数ParetoFraction=0.3，适应度函数值偏差TolFun=10-100,最大进化代数NG=200，停止代数StallGenLimit=200，规模效应系数α=0.5。利用Matlab求解，运行10次得到求解结果，如表3所示。

由表3可知，现有自提模式的自提成本最大为1 035.53元，最小成本为975.15元，平均成本为1 004.56元，平均自提距离为3 062.70 m，平均自提量为1 808个。可以发现自提点覆盖会距离影响服务需求点个数，进而影响自提点的成本和自提量。

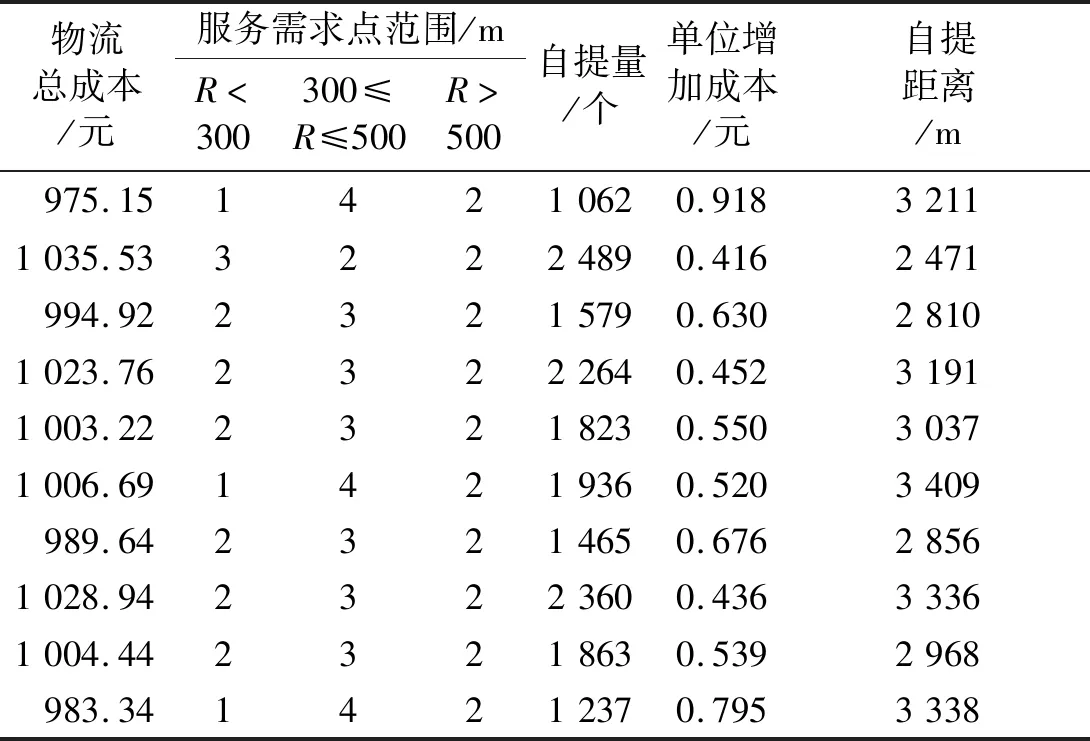
表3 现有自提点的运营情况表

进一步求解自提模式的选址方案，200次迭代寻优前端个体分布如图1所示(目标函数值1为-maxz，其绝对值表示自提量；目标函数值2为minz，表示选址成本)，相应的选址方案如表4所示。由图1可以看出，随着自提量的增加，选址成本也在增加。因此，企业需要基于决策目标在降低成本和提高顾客覆盖度之间权衡。

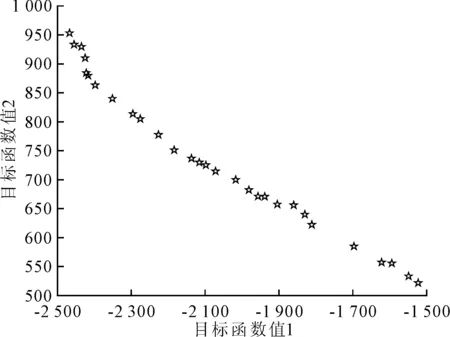
图1 前端个体分布图

从表4可以看出，自提点选址方案中最大成本为931.28元，最小成本为531.68元，平均成本为719.59元，平均成本比现有自提模式成本下降了28.37%；平均自提距离为2 905.8 m，下降了5.12%；平均自提量为2 033个，增加了12.44%。自提点服务距离在300 m以内的需求点平均为3个，占43.0%；服务距离在300～500 m以内的需求点平均为2个，占28.5%；服务距离在500 m以上的点平均为2个，占28.5%，可见服务范围主要集中在500 m以内。由于覆盖距离不同，覆盖需求点个数也不同，实际上顾客会选择服务距离近的自提点，这样会增加该自提点的自提量，成本也会随之增加，因此可以适当增加自提总量换取单位自提成本的减少，从而降低自提总成本。

表4 自提点选址方案

3.2 参数灵敏度分析

为了更好地观察覆盖距离和包裹处理量临界值对选址结果和目标值的影响，对其进行灵敏度分析。

(1)选取不同的R1和R2(最小覆盖距离和最大覆盖距离)，得出不同的目标函数值(自提量、自提成本、单位成本)和自提点选址结果，如图2所示。从图2可以看出，选址方案的分布近似于不连续的上升曲线，图像上的点代表选址方案。在选址方案中，覆盖距离(R1，R2)、自提量、选址成本等之间是相关联的，当R1，R2变化时，导致两个目标函数值也发生变化，特别是对自提总量的影响较为明显，变化幅度为12.33%。结合实际分析，由于用距离描述顾客到自提点的覆盖度差异，且表达式是分段函数，自提点覆盖距离的变化直接影响顾客选择自提服务的意愿。覆盖距离的增大，使得覆盖度降低，虽然会在一定程度上影响顾客的满意度，但随着自提量的增大，相应的成本也在增大。因此C(dij)的减少会导致成本的增长速度变缓。故对于企业而言，当决策者更注重于自提量时，则选择目标函数z2的折中解，但这样会增加成本，而当决策更关注成本时，则选择目标函数z2中的满意解。

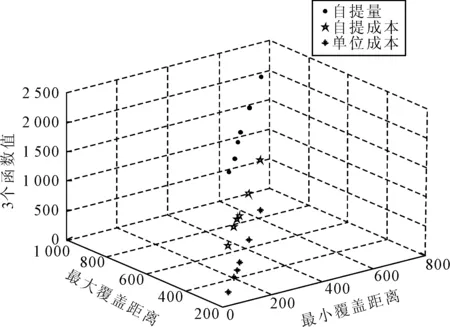
图2 R的灵敏度分析

(2)为获得规模效应，合理设置包裹处理量临界值D2，记录相应的目标函数值，并对其进行灵敏度分析，如图3所示。从图3可以看出，D2的变化对自提量和自提距离影响较大。随着D2的增大，会带来更多的自提量，即总自提量增加大约820个，同时自提距离也在增加，相应的自提成本增加了280元左右，但增加的程度不断降低，表明两者存在“边际递减”的关系。因此，企业可通过增加自提量处理规模效应临界值来获得规模效应，但需对临界值进行合理决策。

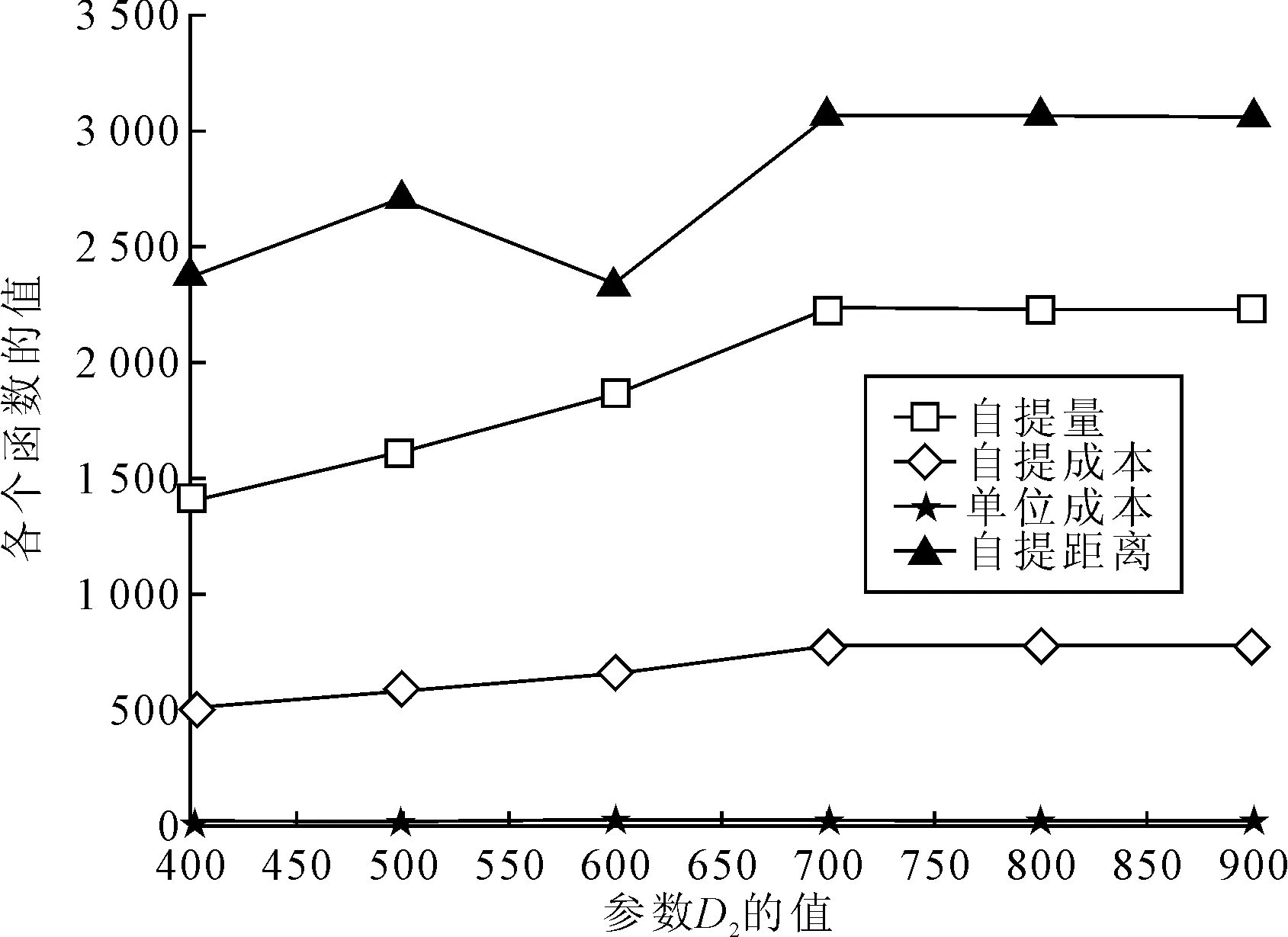
图3 D2的灵敏度分析

4 结论

以自提点处理能力和顾客需求不匹配为背景，探讨了多目标自提点选址问题，通过考虑覆盖度效用、处理量规模约束，构建了带有顾客自提量和企业包裹处理成本的自提点处理量优化模型，采用NSGA-Ⅱ算法和数值模拟对覆盖距离和包裹处理量临界值进行灵敏度分析，验证了模型和算法的有效性，该研究可以为企业节约成本、提高自提点运作效率和顾客服务水平提供借鉴指导。但是研究中假设距离作为主要影响因素描述覆盖度，未考虑服务的时间、安全风险等因素的影响，且忽略顾客需求、位置是变化的，也未考虑选择自提点服务的不确定性和随机性，后续研究可以针对这些问题继续改进。