顾及轨道误差的GNSS卫星钟差实时估计策略优化
2020-09-23刘站科李国鹏陈小英任秀波
刘站科,李国鹏,张 涛,陈小英,任秀波
(自然资源部第一大地测量队,西安 710054)
0 引言
随着北斗三号卫星组网运行并提供服务,北斗卫星导航系统(BeiDou Navigation Satellite Syst-em,BDS)的覆盖能力和服务性能进一步得到提升,更好地助力全球导航卫星系统(Global Navigation Satellite System,GNSS)四系统的导航、定位和授时服务[1-3]。目前,用户对GNSS多系统实时位置服务的精度需求逐步提高,实时卫星钟差产品作为高精度实时位置服务的关键技术,其精度亟需得到提升。
卫星钟差产品作为实时位置服务的重要基础产品之一[4],国际GNSS服务组织(international GNSS Service,IGS)与我国自主建立的国际GNSS监测评估系统(International GNSS Monitoring and Assessment System,iGMAS)均致力于优化多系统融合的卫星钟差实时估计的精度。IGS已推出全球定位系统(Global Positioning System,GPS)/全球卫星导航系统(Global Navigation Satellite System,GLONASS)卫星钟差实时产品,其精度可达到0.3~0.8ns。GPS超快速卫星钟差产品的预报部分可满足实时性要求,但其精度为3ns,虽略优于钟差精度为5ns的广播星历产品,但仍不能满足实时定位的高精度需求[5]。陈良等通过优化待估参数,实现了简单高效的多GNSS实时钟差估计模型,GPS卫星钟差实时精度约0.22ns,地球静止轨道(Geostationary Earth Orbits,GEO)卫星优于0.5ns,倾斜地球同步轨道(Inclined GeoSynch-ronous Orbit,IGSO) /中地球轨道(Medium Earth Orbit,MEO)卫星优于0.24ns,Galileo卫星优于0.32ns[6]。谷守周和施闯等通过优化BDS/GPS随机模型,显著提高了BDS/GPS的实时估计精度[7]。耿长江等通过优化钟差融合解算模型,利用滤波算法实现了BDS/GPS实时钟差融合估计,其实时钟差产品用于动态精密单点定位(Precise Point Positioning,PPP)的定位精度与事后产品相当[8]。BDS/GPS单系统或双系统实时钟差产品已经成熟,其四系统联合估计的实时钟差产品处于测试运行阶段。因此,针对GNSS四系统的卫星钟差联合估计的精度提升,实现策略优化,满足厘米级位置服务的需求,成为技术层面亟需解决的难题。
本文以iGMAS中国测绘科学研究院北斗分析中心为平台,在实现GNSS四系统实时卫星钟差联合估计的基础上,分析了不同卫星系统的轨道误差,设计了一种顾及轨道误差的权函数模型,进行策略优化,并采用IGS与iGMAS的实测数据进行精度评估,验证了此策略的可行性。
1 GNSS卫星钟差实时估计算法
GNSS卫星钟差实时估计是基于GNSS实时卫星观测数据,固定卫星轨道等精密信息,并利用模型修正相位缠绕和固体潮等误差,实现卫星钟差估计[4]。钟差实时估计一般采用非差估计算法[5]。非差估计算法的GNSS误差观测方程为
(1)
式中,S为GPS/BDS/GLONASS/Galileo卫星系统;r为地面观测站;n为当前历元的第n颗卫星;P为伪距观测值,Φ为相位载波观测值;dclkr为接收机钟差;dclkS,n为卫星钟差;br为接收机端信号延迟;bS,n为卫星端信号延迟;m为r测站跟踪某一颗卫星时的对流层投影函数;ztdr为天顶对流层湿延迟值;N为非差无电离层组合观测值的模糊度;l为伪距或载波观测值与卫星到测站位置的几何距离的差;v为误差改正数。
2 顾及轨道误差的GNSS卫星钟差实时估计策略优化
实时卫星钟差估计时,通常将轨道改正信息固定为超快速预报轨道,且采用6h更新的超快速轨道,而本文为降低轨道误差,采用3h更新的四系统超快速轨道。但是预报轨道仍然存在弧段间的跳跃[4],对实时钟差估计精度具有一定的影响。因此,从卫星轨道出发,研究其误差对卫星钟差估计的影响,并对钟差估计进行策略优化,以期提高估计精度。
2.1 卫星轨道误差影响分析
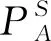
(2)
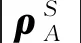
如图1所示,由轨道误差引起的测距误差(即径向和切向轨道误差在视线上的投影)等价于
(3)
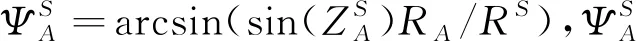
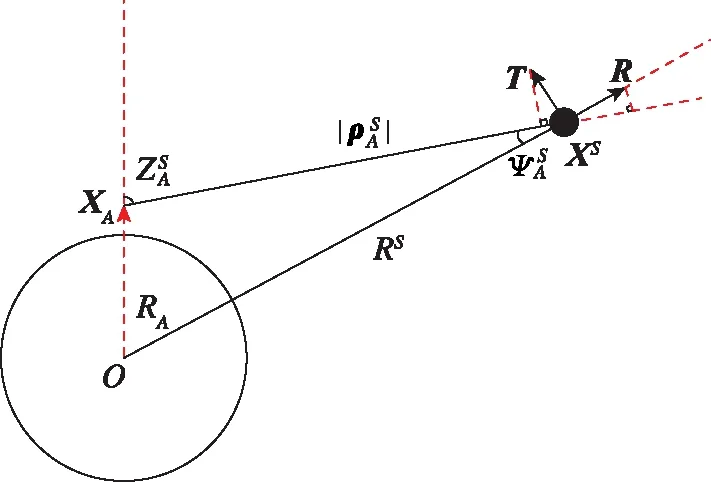
图1 轨道误差在信号传播方向上的投影Fig.1 Projection of orbit error in the direction of signal propagation
如表1所示,从GNSS各系统轨道误差分别对卫星钟差估计的影响来看:卫星钟差对径向轨道误差具有很强的吸收能力,最高可达98.8%。卫星钟差对切向轨道误差也有所吸收,最高可达25%。由此可知,卫星钟差中融合了卫星轨道误差,且卫星轨道误差可对卫星钟差精度产生影响。GNSS卫星对地面测站的最大可视角度为14.5°,而观测站对卫星观测的可视角度会影响GNSS的观测质量,从而在一定程度上对卫星钟差精度产生影响。因此,对卫星钟差估计精度的提高可以从卫星轨道误差方面进行研究。

表1 轨道误差对卫星钟差估计的影响
2.2 权函数模型优化
GNSS观测值为卫星和观测站之间的距离,此观测值已融合卫星轨道误差。因此,本文从卫星与测站之间距离的数学模型出发,对GNSS观测值进行权值确定,设计融合卫星轨道误差的权函数,优化随机模型[8],以提高实时卫星钟差估计精度。
距离观测在高精度测距定位应用中建立平差函数模型时,除了确定待定点的点位坐标参数,还需要附加误差参数[11-13]。薛树强等在测距定位观测方程非线性分析的基础上,导出了有关长距离函数二阶残余项的估计公式,距离函数的二阶泰勒展开项可转变为二阶残余项[15-18]。
卫星与观测站距离的测距定位观测方程可表示为
(4)
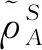
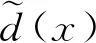
(5)

(6)
(7)
由于GNSS长距离问题的二阶项公式可精确到距离统计量的方差信息,即
(8)
(9)
(10)
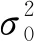
(11)

基于观测值的轨道误差和高度角对其权值的影响,可综合考虑轨道误差和卫星高度角对钟差估计精度的影响,联合确权,设计权函数(如式(12)),实现随机模型的优化。
(12)
3 数据处理分析
3.1 实验方法
实验中采用iGMAS和IGS的实时数据,实时获取80个左右的观测站数据以及导航星历。利用相同数据源的实时数据作为解算数据且使用相同的解算策略,如表2所示。基于不同权函数的设计方案,同时进行2018年年积日第10天~第24天(共计15天)的GNSS卫星钟差解算,将不同方案的钟差实时估计结果与GBM的精密钟差进行对比,得到各系统各天的精度结果。精度比对过程中,选取德国地学研究中心(German Research Centre for Geosciences,GFZ)提供的GBM最终钟差产品作为参考,目前GFZ作为最早提供高采样率的GNSS四系统卫星钟差的研究机构,其卫星轨道和钟差产品的稳定性好、精度高。GBM轨道产品较IGS最终产品精度优于1cm,钟差优于0.02ns。比较并分析两种方案的卫星钟差估计精度。

表2 实时钟差估计策略
实验方案为:方案一:权函数模型考虑卫星轨道误差影响,并对高度角加权;方案二:权函数模型仅考虑高度角加权。
3.2 实验结果分析
年积日第10天~第24天,两种方案的GPS卫星钟差精度如图2所示,GLONASS卫星钟差精度如图3所示,BDS卫星钟差精度如图4所示,Galileo卫星钟差精度如图5所示。将各系统各天的卫星钟差的实时精度求取平均值,如表3所示。
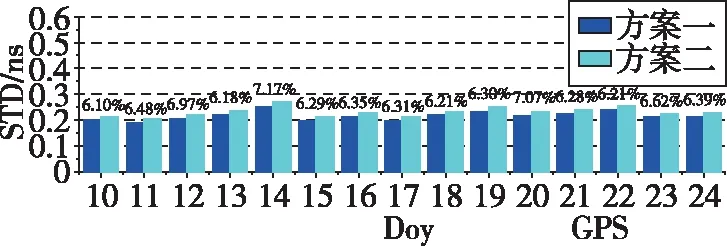
图2 GPS卫星实时钟差精度Fig.2 GPS satellite real-time clock offset accuracy
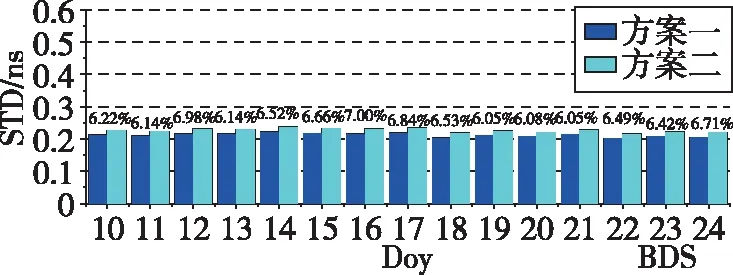
图3 BDS卫星实时钟差精度Fig.3 BDS satellite real-time clock offset accuracy
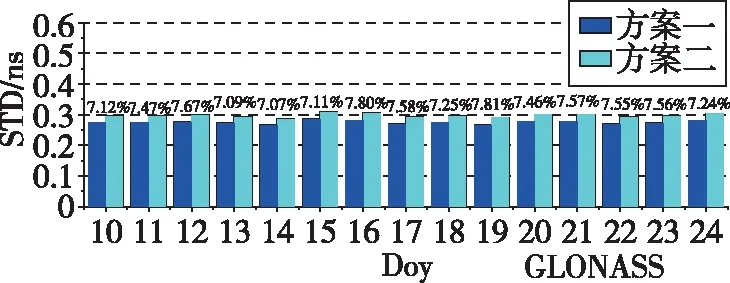
图4 GLONASS卫星实时钟差精度Fig.4 GLONASS satellite real-time clock offset accuracy
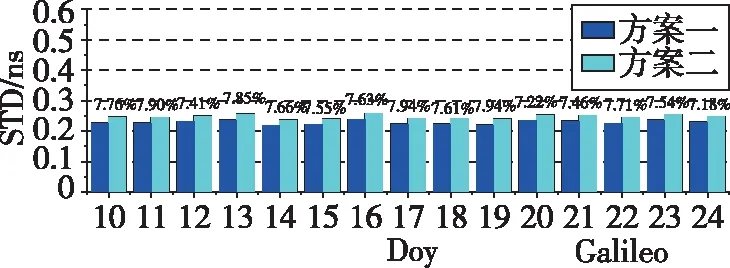
图5 Galileo卫星实时钟差精度Fig.5 Galileo satellite real-time clock offset accuracy
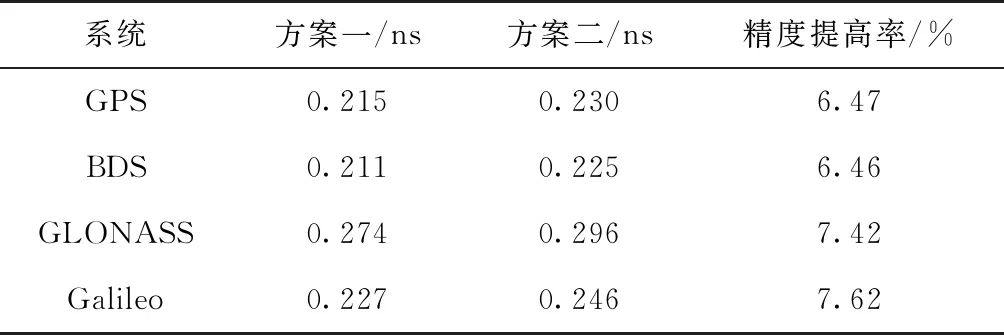
表3 年积日第10天~第24天两种方案的卫星钟差实时精度
由此实验的精度结果图2~图5及表3可知:
1)GPS中,各天中方案一的精度均明显优于方案二的精度,两种方案整体精度优于0.269ns。方案一的精度最高可达0.197ns,最低不超过0.250ns。相较于方案二,方案一的提高率最高可达7.17%,最低为6.10%,且提高率在6.50%附近波动。方案一的平均精度为0.215ns,方案二的平均精度为0.230ns,平均提高率为6.47%。
2)BDS中,各天中方案一的精度明显优于方案二的精度,两种方案整体精度优于0.236ns。方案一的精度最高可达0.201ns,最低不超过0.221ns。相较于方案二,方案一的提高率最高可达7.00%,最低为6.05%,且提高率在6.50%附近波动。方案一的平均精度为0.211ns,方案二的平均精度为0.225ns,平均提高率为6.46%。
3)GLONASS中,各天中方案一的精度同样优于方案二的精度,两种方案整体精度优于0.307ns。方案一的精度最高可达0.266ns,最低不超过0.285ns。相较于方案二,方案一的提高率最高可达7.81%,最低为7.07%,且提高率在7%附近波动。方案一的平均精度为0.274ns,方案二的平均精度为0.296ns,平均提高率为7.42%。
4)Galileo中,各天中方案一的精度同样优于方案二的精度,两种方案整体精度优于0.257ns。方案一的精度最高可达0.218ns,最低不超过0.237ns。相较于方案二,方案一的提高率最高可达7.94%,最低为7.18%,且提高率在7.50%附近波动。方案一的平均精度为0.227ns,方案二的平均精度为0.246ns,平均提高率为7.62%。
综合各系统各天的分析结果可知,相比方案二(即原来的方案),方案一可有效提高每个系统的整体解算精度,证明了此优化策略的可行性。GPS实时钟差精度平均提高6.47%,BDS平均提高6.46%,GLONASS平均提高7.42%,Galileo平均提高7.62%。
因此,顾及卫星轨道误差的权函数模型,能够对卫星钟差估计进行策略优化,可有效提高GNSS各系统实时卫星钟差的整体精度。
4 结论
本文在实现GNSS四系统实时卫星钟差联合估计的基础上,为提高GNSS卫星钟差实时估计精度,提出了估计优化策略。针对GNSS各系统的轨道差异,在分析各系统卫星轨道误差对钟差估计影响的基础上,基于距离函数线性化二阶残余项的思想,提出了一种顾及轨道误差的权函数模型,可有效提高实时精度。GPS钟差实时精度达到0.215ns,平均提高6.47%;BDS精度达到0.211ns,平均提高6.46%;GLONASS精度达到0.274,平均提高7.42%;Galileo精度达到0.227ns,平均提高7.62%。
对GNSS卫星钟差实时估计策略的研究,可从数学模型的角度出发,为多系统的定位授时等解算提供借鉴。此顾及轨道误差的权函数模型作为一种优化策略,可有效提高多系统解算的精度,满足实时定位的精度需求。然而,四系统的联合解算增加了估计参数的数量,延长了估计时间,因此在满足精度要求的条件下,如何提高解算效率,保证产品的实时性,成为下一步的研究方向。
