混沌蝙蝠算法UAV 网络控制系统故障诊断策略*

何燕燕

（江苏商贸职业学院电子信息学院，江苏 南通 226011）

0 引言

目前，由于网络技术的快速发展，网络控制系统在大型无人机发动机控制系统上的应用上也越来越受人关注［1-2］。网络控制系统与传统的点对点控制系统相比，最大的不同在于其相关数据是通过总线进行传输，但是也正是由于总线的存在导致其诱导时延以及数据丢包等问题，使得在进行故障诊断时必须将总线带来的不利因素考虑进去。文献［3］为离散时间延迟系统设计了功能强大的故障检测观察器。这样可以检测出残差，并为嘈杂的信号提供更好、更鲁棒的性能。文献［4-6］使用H∞理论对不确定系统，时滞网络控制系统和非线性系统执行鲁棒的故障检测，因此，即使在强噪声条件下，该系统也表现出色。可以保证故障的检测性能。然而，以上文献仅考虑了提高检测系统抵抗噪声干扰信号的鲁棒性方法，而不是考虑对干扰信号的影响。

为同时提升检测系统对噪声信号的鲁棒性以及故障信号的敏感性，本文针对双通道多包传输的短时变时延无人机发动机网络控制系统，提出了一种基于改进蝙蝠的故障检测观测器优化设计方法。首先对原系统建立故障观测器，将双通道多包传输转换为在系统之间切换，以将短期波动延迟建模为系统不确定性的一种。接下来，残余信号的传递函数和噪声信号与故障信号的比率建立为优化的目标函数，为使得残差信号对故障信号敏感，对噪声鲁棒，利用改进蝙蝠算法在保证观测器残差系统稳定的条件下使得目标函数最小，从而求得最优故障观测器增益矩阵。

1 系统建模

首先建立短时变时延无人机发动机网络控制系统，做以下合理的假设：

1）传感器、控制器、执行器均为事件驱动，周期为T。2）忽略计算时间带来的延迟。3）系统通过静态调度实现。4）忽略数据包丢和数据包错乱。

考虑到UAV 发动机在实际运行过程中可能会存在外界扰动或者模型建立的误差，因此，文献［7］将这些因素统一考虑为系统的模型不确定性。已知该发动机某一稳态点的不确定离散时间模型为：

传感器将数据发送给控制器的每个控制状态量封装在多个数据包中，并且将从每个控制器发送数据给执行器的每个控制状态量封装在不同数据包中，因此，每个控制器和系统通过执行指令的机制接收传感器执行指令的状态量x（k）与执行器的控制量u'（k）分别为x'（k）与u（k）。

静态调度的应用使得可以将多数据包传输转换为具有两个交换机的交换系统。当在k 时刻，开关K1和Si（i=1，2，…，m）连接，而开关K2则和Sj'（i=1，2，…，m）连接，此时，未发送的数据分组被认为是分组丢失，令k-1 时刻的数据替代。当前正在发送传输状态和控制变量，并且此时的数据变为当时的状态。因此，存在如下关系：

2 改进BA 算法

蝙蝠优化算法的原理为：在飞行过程中，蝙蝠不断发射并接受频率变化的声波脉冲，并且根据从周围反射回来的声波确定猎物位置并躲避障碍物［8-10］。蝙蝠种群发出的超声波由谐波类宽频带的调频信号组成，频率范围：25 KHz～100 KHz，假设空气的速度为340 m/s，波长与频率f 的关系为：

通过模拟蝙蝠群，该算法可以模拟在空间中移动，检测目标，捕获目标并避开障碍物的生物过程。最后，可以计算近似于全局最优问题的近似全局最优解［11］。

每个蝙蝠在搜索空间中的位置对应于解空间中的解，具有与脉冲声波的响度相对应的辐射速度与脉冲声波辐射适应度的频率函数之比。蝙蝠种群系统可以同时检测更新的脉冲声波。使用特定的发射频率，脉冲声脉冲速率和其他脉冲波的声脉冲响度，从而可以快速生成一组新的脉冲声发射解决方案。然后，逐渐演变为包括全局最优解或近似全局最优解［12］。迭代过程的公式如下：

当算法收敛到最优解域时，种群位置受到干扰，更准确地达到了使用局部函数搜索的主要目标，并保证了最优解的收敛性。更新公式为：

公式α 学函数是［-1，1］声学函数间隔内的随机数；Al为第l 代蝙蝠和其他种群的平均声音响度。

基于式（12），随着迭替换代的过程持续不断进行，更新各个电波参数对所有蝙蝠和人类群体的电波影响度被称为蝙蝠脉冲电波发射的频率Ri和其对蝙蝠的群体脉Ai冲波影响度。本次软件更新的计算公式基本定义如下：

式中，β，ω 为常数，β＞0，0＜ω＜1。

BA 在寻优过程中具有良好的收敛性和较大的搜索范围，但其位置的更新仅依赖蝙蝠种群的速度参数，且缺乏一定的多样性，导致算法后期种群聚集的现象较为严重［13-14］。为弥补这一缺点，本文对基本BA 进行变异操作，具体步骤如下：

Step1：设置蝙蝠种群的交叉比例和交叉方法，例如选取适应度值排名前50%的个体进行两两配对，对该50%的个体组成的种群分别进行两次交叉运算，将产生的数量相同的个体并替换为下一代的后50%个体，位置的交叉公式如（15）所示：

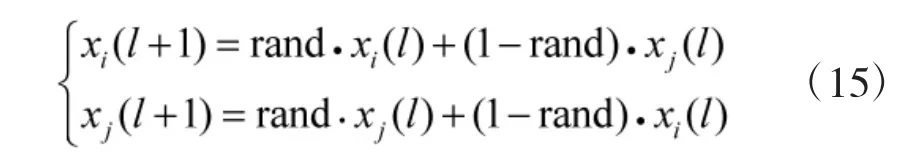
Step2：引入变异激活函数，对更新后的xi（t+1）进行变异操作，变异激活函数是蝙蝠个体是否进行变异操作关键，变异激活函数为：

Step3：对满足Step2 中激活函数条件的蝙蝠个体进行变异操作—均匀变换或高斯变换，均匀变换通过对位置的更新，将使得部分个体表现为以更快的速度向最优解区域进行收敛，高斯变换则主要解决算法在迭代后期易陷入局部极值的情况，由于蝙蝠种群在迭代后期将在最优解区域附近以微扰动的方式重新生成，此时的搜索已无法扩展至更大的范围，而高斯变换将在条件满足的情况下，将变异个体脱离最优解的限制，均匀变换与高斯变换的实现方法如下：

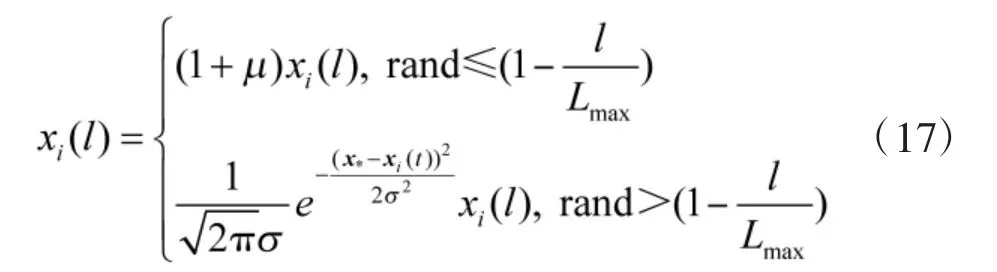
式中，σ 为高斯分布的标准差，由式（15）与式（16）可看出，变异操作的引入使得BA 种群内部的生物多样性得到了提高，加快了全局搜索速度，同时，在局部寻优过程中，能够避免最优解位置对种群整体的影响，避免陷入局部极值点。

图1 混沌BA 和基本BA 脉冲发射率

综上所述，改进BA 的实现步骤如下：

Step2：根据式（15）及适应度值排名对蝙蝠种群进行交叉运算，并根据式（16）确定蝙蝠个体是否触发变异操作，若Activate（k）＜1，则按照式（17）进行均匀变换或高斯变换；

Step5：找出当前种群内所有蝙蝠个体目标函数的记录最高值和最高值的位置。

步骤6：然后重复执行步骤2～步骤5，直到输出全局预优化的最佳解决方案或算法达到最大迭代的次数，然后再次输出全局最优算法的解。

3 改进BA 的故障检测观测器设计

设闭环观测器为：

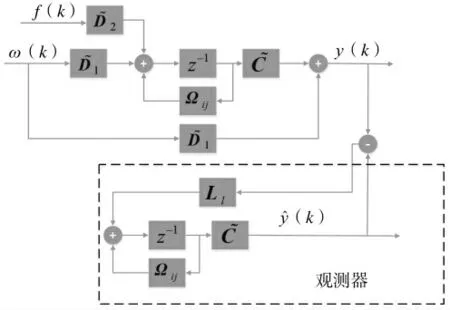
图2 观测器结构

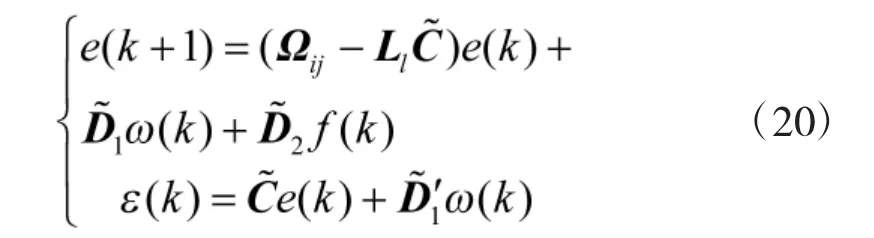
由于式（20）表示出了观察者的误差条件和输出等式，所以式（20）的Z 变换可以将残余信号ε 传递到干扰信号ω 和故障信号f 传递函数矩阵：

式中，Gf为残差信号ε 到故障信号f 的传递函数矩阵，Gω为残差信号ε 到扰动信号ω 的传递函数矩阵。

在本节中，将使用改进的BA 优化故障检测观察器增益矩阵Ll进行优化：

首先需要满足稳定性要求，这是故障检测的基础。由文献［3］获得稳定性的条件如下：

根据文献［6］的规则，将式（23）代入其中的一个函数式（22），该函数等式的取值变为ηl＞0（l=1，2，…，m×n），使得

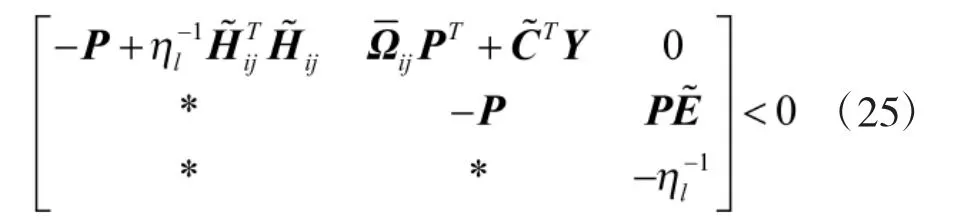
稳定性满足以下条件：观测器的增益矩阵Ll必须在一个满足对称正定增益矩阵P 的条件下存在ηl＞0（l=1，2，…，m×n），使得式（25）成立。

为了提高误差观测器的鲁棒性和灵敏度，适应度函数为

包含J1相对于整个噪声系统的ωr噪声频率和噪声信号的频率点的噪声传递函数增益。J1应尽可能小，以减少噪声对系统的影响［15］，因为传感器或执行器J2故障信号主要集中在低频段。优化的目的是使拟合函数最小，因为拟合函数应尽可能大，以使系统对故障信号更敏感。

总之，基于改进的BA 算法的故障检测可以归纳为以下优化问题：

具体的优化步骤为：

Step1：改进BA 的参数初始化。

Step2：每次获得的最佳位置均被计入式（27）中的线性矩阵不等式，以利用改进的BA 进行优化。如果有可行的解决方案，优化将继续。否则，将重复位置搜索。

Step3：迭代函数停止算法，并且需要确定替代次数Iterate_times 是否已经低于达到最大迭代的次数。当满足条件时，迭代函数将停止算法，并输出自适应函数的极值。对应于迭代函数的算法到达障碍观察者的最佳迭代位置和最佳增益矩阵Ll。否则，请返回到步骤3，并在下一次迭代中运行优化。

4 仿真算例及结果分析

4.1 控制系统半物理仿真平台

本文通过飞机发动机分布式控制仿真系统的半分布式物理仿真系统平台结构，设计并进行了该控制系统的仿真验证。图3 显示了系统结构设计框架思路。该系统主要包括：仿真计算机和控制器、智能执行器和智能传感器以及CAN 总线。仿真计算机实现发动机数学模型的仿真。智能传感器实现数据测量以及初步转换并将其通过CAN 总线传至控制器。控制器实现相应的控制功能，并输出控制信号控制智能执行机构。智能执行器收到CAN 总线的数据之后实现相应的控制行为。整个过程实现闭环控制，系统照片如图4 所示。

图3 系统的半物理平台结构

4.2 基于半物理平台的仿真

设无人机发动机的状态方程为：

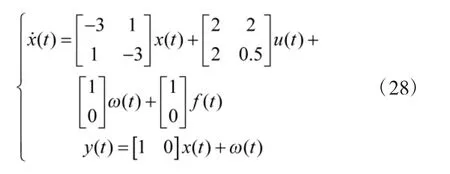
图4 网络控制系统仿真平台实物

设置采样周期时间T=20 ms 可得

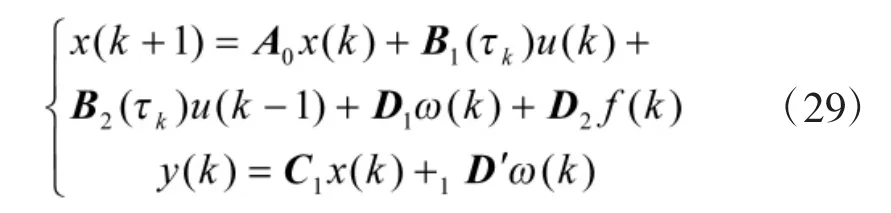
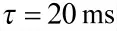
分别使用基本蝙蝠算法和改进蝙蝠算法来实现观测器寻优，如图5 和表1 所示表示某一个观测器的优化结果。

图5 优化结果对比图

从图5 和表1 中可以看出，改进蝙蝠优化的到达极小值时的收敛速度比基本BA 快9 个迭代周期。且改进蝙蝠优化算法收敛曲线无明显的转折，进一步证明该方法不易陷入局部最优。这表明改进蝙蝠算法具有更好的优化效果。

表1 优化结果对比表

第4 个数据位是CAN 总线。由于系统发送的数据量很少，因此，数据包的数据量仅为在半物理平台上模拟双通道多数据包传输所需的3 位。发送的数据包设置在数据包的标志位中。图6 显示了发送设置数据包的随机序列。

图6 数据包的随机传输顺序

传感器发生短路故障，则状态变量会出现一个突变，该种故障模式与阶跃型故障十分类似，故通过阶跃故障来模拟短路故障，对系统施加一个幅值较小的阶跃型故障，当添加了一幅度为0.92 的干扰信号。检测结果如图7 和图8 所示，分别显示了经典检测方法以及改进的BA 优化检测方法的结果。经典方法的残差信号的抖动幅度为0.12，而优化方法的残差方法的振动幅度仅为0.069，表明添加的干扰对经典检测方法会产生显著的影响，使得设置阈值并不能完全区分状态。而提出的检测方法对故障信号实现了显著的放大，另外还大大降低了干扰信号幅值。提出的方法使得阈值设置范围从经典方法的0.12～0.166 增加至0.069～0.202。该范围扩大了3.52倍，表明该方法有助于区分故障状态和正常状态。

图7 传统鲁棒观测器检测残差

图8 改进BA 观测器检测残差

图9 边坡故障残差比较

进一步给定一个传感器的非线性故障：

添加一幅值为0.08 的噪声信号。图10 展示了检测残差的比较结果。经典方法的残留振动约为0.004 2，优化方法的残留振幅为0.002 2。结果表明，噪声信号对传统的检测方法影响很大。此外，优化方法的阈值选择范围是0.002 2～0.018 4，而经典方法的阈值选择范围是0.004 2～0.008 3，相当于优化方法的阈值选择范围相比经典方法增大4.12 倍。此外，证明了这种优化方法可以更好地辨别故障和正常情况。

图10 非线性故障检测残差的比较

总之，改进的BA 优化的观察者增益矩阵可以将干扰信号放大，并减少噪声的影响。这样可以有效降低故障误诊率，有效提高故障检测的准确性。

5 结论

针对总线条件下具有双通道多包传输的短时变时延无人机发动机控制系统，提出一种基于改进蝙蝠优化算法的发动机故障检测算法。仿真结果表明：

1）在不同的丢包情况下能够保证系统的收敛性与稳定性。

2）改进蝙蝠算法比基本蝙蝠算法在优化准确率上更高。

3）提出方法不仅可以抑制噪声信号对残余振幅的影响，而且可以提高故障状态与正常状态之间的区别度，使得阈值选择具有更大的容错范围与选择空间，有效改善各种故障类型的检测效果。

在本文中，该方法仅限于稳态UAV 发动机故障检测，并且需要进一步全包线非线性模型的故障。