Z-连通极小集及其应用

赵 娜

（1.长治医学院数学教研室，山西长治046000； 2.陕西师范大学数学与信息科学学院，陕西西安710119）

Domain理论自20世纪70年代创建以来备受关注，其中研究的一个重要分支是尽可能将Domain理论推广到更一般的格序结构［1-3］.1977年，Hutton［4］在完全分配格上引入了极小族概念，证明了完全分配格的每个元都有极小族.自此，极小集（更一般地，φ-极小集）理论得到了广泛的应用，并产生了一系列较深刻的结果［5-13］.文献［5］引入并讨论了完备格上的极大族与极小族理论，给出完全分配格的一个构造定理.文献［6］证明了φ-极小集存在与完全分配律等价.文献［7］以拟极小集为基础，证明了拟极小集存在与连续偏序集等价，并对Lawson和Hoffmann所确立的完全分配格与连续偏序集间的对应关系给出了一种新处理.文献［8-13］分别论述了一些具体序结构的极小集刻画.本文在文献［5-13］的基础上引入Zc-极小集的概念，给出Zc-连续偏序集及保Zc-集的并且保≪Zc的映射的Zc-极小集刻画，得到了保Zc-集的并且保≪Zc的映射的扩张定理.

1 预备知识

定义 1.1［14］设 P 是偏序集，Ø≠S⊆P.若∀x，y∈S，∃xi∈S，i＝1，2，...，n，使得 x＝x1，xn＝y，且∀i＝1，2，...，n-1，xi，xi＋1可比较，则称 S 是连通的，x与y在S中连通.

定义 1.2［14］设 POS 是以偏序集为对象，保序映射为态射的范畴，设C是POS的一个子范畴，C上的一个连通集系统Zc是一个映射，其中对C的每一个对象 P，Zc（P）是 P的连通子集构成的子族，且满足下列条件：

1）∀x∈P，↓x∈Zc（P）；

2）若 f：P→Q 是 C 中的态射，则∀D∈Zc（P），↓f（D）∈Zc（Q）；

3）对C的每一个对象 P，Zc（P）还是 C的对象，其中Zc（P）的序是通常的包含关系.

设P是偏序集.称Zc（P）中元素为Zc-子集.若∀D∈Zc（P），∨D存在，则称P是Zc-完备的.记↓IZc（P）＝｛↓D｜D∈Zc（P）｝，IZc（P）中的元素称为Zc-理想.易证P是Zc-完备的当且仅当P的每个Zc-理想在P中上确界存在.

本文仅考虑POS上的连通集系统.

注 1.3Z-连通集系统和Z-子集系统［2］是POS上的2个不同的子集系统.对于偏序集P，根据Z-连通集系统和Z-子集系统的定义可以验证：

1）Zc（P）＝｛↓x｜x∈P｝是 Z-连通集系统，不是Z-子集系统；

2）Z（P）＝｛F｜F是 P的有限子集｝是 Z-子集系统，不是Z-连通集系统；

3）Zc（P）＝｛D｜D 是 P 的定向子集｝既是Z-连通集系统，也是Z-子集系统.

定 义 1.4［14］设 P 是 偏 序 集.若 对Zc（IZc（P））中任意 Zc- 集 D，都有∪D∈IZc（P），∪D＝∨D，则称连通集系统Zc是并完备的.

定义 1.5［14］设 P 是 Zc-完备偏序集，x，y∈P.若∀D∈Zc（P），y≤∨D，∃d∈D，使得 x≤d，则称 x≪Zcy.记⇓Zcx＝｛y∈P｜y≪Zcx｝.

性质 1.6［14］设 P 是 Zc-完备偏序集.若x≪Zcy≤z（x≤y≪Zcz），则 x≪Zcz.

定义 1.7［14］设 P 是 Zc-完备偏序集.若∀x∈P，有：

1）⇓Zcx∈Zc（P）；

2）x＝∨⇓Zcx，则称P是Z-连通连续偏序集，简记为Zc-连续偏序集.

定义 1.8［14］设 P 是 Zc-完备偏序集，F⊆P.若F满足：

1）F＝↓F；

2）∀D∈Zc（P），D⊆F，则∨D∈F.

则称F是 Zc-闭集.记 P的 Zc-闭集全体为ΓZc（P）.Zc-闭集的补集称为 Zc-Scott开集.全体Zc-Scott开集构成一个拓扑，称为Zc-Scott拓扑，记作 σZc（P）.

命题 1.9［15］设 P 是 Zc-完备偏序集，U⊆P.U是Zc-Scott开集当且仅当U满足：

1）U＝↑U；

2）∀S∈Zc（P），∨S∈U，则 S⊆U≠Ø.

2 Z c-极小集及Z c-连续偏序集的Z c-极小集刻画

定义 2.1设 P是 Zc-完备偏序集，x∈P，D∈Zc（P），若 D 满足如下条件：

1）x＝∨D；

2）若∀S∈Zc（P），x≤∨S，则∀d∈D，∃s∈S，使得d≤s，则称D是x的一个Zc-极小集.

注2.21）Zc-极小集的并未必是Zc-极小集.故若x有Zc-极小集，则未必有最大的.

2）定义2.1中若将条件 D∈Zc（P）改为 D⊆P，则称D是x的一个广义Zc-极小集.广义Zc-极小集的并是广义Zc-极小集.故若x有广义Zc-极小集，则必有最大的.

3）Zc-极小集是广义Zc-极小集.当Zc（P）是P中所有定向集之族，则此时的广义Zc-极小集是文献［8］中定向极小集的推广.

命题2.3设P是Zc-连续偏序集，x∈P，则⇓Zcx是x的最大Zc-极小集.

证明由Zc-连续偏序集及≪Zc的定义可知⇓Zcx是x的Zc-极小集.设D是x的任一Zc-极小集，取S＝⇓Zcx，由Zc-极小集的定义知∀d∈D，∃s∈⇓Zcx，使得 d≤s.从而 d≪Zcx，即 D⊆⇓Zcx，⇓Zcx是x的最大Zc-极小集.

定理2.4设 P是 Zc-完备偏序集，x∈P，⇓Zcx∈Zc（P）.则下列条件等价：

1）P是Zc-连续偏序集；

2）∃D∈Zc（P），D⊆⇓Zcx，∨D＝x；

3）∃D∈Zc（P），∨D＝x，↑x＝∩｛⇑Zcd｜d∈D｝；

4）x有Zc-极小集.

证明1）⇒2）取D＝⇓Zcx即可.

2）⇒3）∀d∈D，d≪Zcx，从而当 x≤y时，有d≪Zcy，即↑x⊆∩｛⇑Zcd｜d∈D｝.反之，若 a∈∩｛⇑Zcd｜d∈D｝，则∀d∈D，d≪Zca.由此可知x＝∨D≤a，即∩｛⇑Zcd｜d∈D｝⊆↑x.

3）⇒4）∀S∈Zc（P），x≤∨S，则∨S∈↑x＝∩｛⇑Zcd｜d∈D｝，从而∀d∈D，d≪Zc∨S.由≪Zc的定义知∃s∈S，使得 d≤s，即 D是 x的 Zc-极小集.

4）⇒1）设D是x的一个Zc-极小集，则D⊆⇓Zcx，x＝∨D≤∨⇓Zcx≤x.从而 x＝∨⇓Zcx，即 P是Zc-连续偏序集.

推论2.5设P是Zc-连续偏序集，x∈P.则下列条件等价：

1）D是x的Zc-极小集；

2）D∈Zc（P），D⊆⇓Zcx，∨D＝x；

3）D∈Zc（P），∨D＝x，↑x＝∩｛⇑Zcd｜d∈D｝；

4）D∈Zc（P），⇓Zcx＝↓D.

证明由定理2.4的证明过程及Zc-连续偏序集的定义可得.

引理 2.6［14］设 Zc是并完备的连通集系统.若P是Zc-完备偏序集，则P上的≪Zc关系满足插入性质，即 x≪Zcy⇒∃z∈P，x≪Zcz≪Zcy.

定理2.7设Zc是并完备的连通集系统，P是Zc-完备偏序集.则P是Zc-连续偏序集当且仅当P满足如下性质：

1）∀x∈P，⇓Zcx∈Zc（P）；

2）插入性质：∀x，y∈P，x≪Zcy⇒∃z∈P，x≪Zcz≪Zcy；

3）｛⇑Zcx｜x∈P｝是 σZc（P）的基；

4）∀x∈P，↑x＝∩｛U∈σZc（P）｜x∈U｝.

证明必要性 1）和2）分别由Zc-连续偏序集的定义及引理2.6直接可得.

3）显然⇑Zcx 是上集.∀S∈Zc（P），∨S∈⇑Zcx，即 x≪Zc∨S.由≪Zc满足插入性质知∃p∈P，使得x≪Zcp≪Zc∨S.故∃s∈S，使得 x≪Zcp≤s，则x≪Zcs，即⇑Zcx∩S≠Ø，因此⇑Zcx∈σZc（P）.

下证∀U∈σZc（P），U＝∪｛⇑Zcx｜x∈U｝.显然有∪｛⇑Zcx｜x∈U｝⊆U.反之，∀x∈U，⇓Zcx∈Zc（P），∨⇓Zcx＝x，则⇓Zcx∩U≠Ø.从而∃u∈U，使得 u≪Zcx，即 x∈⇑Zcu，U⊆∪｛⇑Zcx｜x∈U｝.

4）由3）及定理2.4知

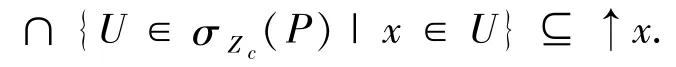
反之，由Zc-Scott开集是上集知↑a⊆U，即↑x⊆∩｛U∈σZc（P）｜x∈U｝.

充分性 由3）和4）知↑x＝∩｛⇑Zca｜a∈⇓Zcx｝.下证 x＝∨⇓Zcx.显然有∨⇓Zcx≤x.反之，∀a∈⇓Zcx，由2）知∃p∈P，使得 a≪Zcp≪Zcx，即 p∈⇓Zcx.则a≪Zcp≤∨⇓Zcx.从而a≪Zc∨⇓Zcx.故∨⇓Zcx∈∩｛⇑Zca｜a∈⇓Zcx｝＝↑x，即∨⇓Zcx≥x.

3 保Z c-集并和≪Z c的映射的Z c-极小集刻画及扩张定理

定义 3.1［14］设 P、Q 是 Zc-完备的偏序集，f：P→Q 是映射.若∀S∈Zc（P），f（∨S）＝∨f（S），则称f保Zc-集的并.

注3.2设映射 f：P→Q保 Zc-集的并，则 f是保序的，即 x≤y⇒f（x）≤f（y）.

定义 3.3设 P、Q是 Zc-完备的偏序集，f：P→ Q 是 映 射.若 ∀x，y∈ P，x ≪Zcy⇒f（x）≪Zcf（y），则称 f保≪Zc.

定义 3.4设P、Q是Zc-完备的偏序集，f：P→Q是映射.若∀x∈P，D是x的Zc-极小集，则↓f（D）是f（x）的Zc-极小集.则称f保Zc-极小集.

定理3.5设f：P→Q是Zc-连续偏序集间的映射.则下列条件等价：

1）f保Zc-集的并且保≪Zc；

2）f保 Zc- 集 的 并 且 ∀x∈P，f（⇓Zcx）⊆⇓Zcf（y）；

3）f保 Zc- 集 的 并 且 ∀x∈P，f（⇑Zcx）⊆⇑Zcf（y）；

4）f保序且f保Zc-极小集；

5）f保 Zc- 集 的 并 且 ∀x∈P，↑f（x）⊆∩｛⇑Zcf（y）｜y∈⇓Zcx｝.

证明1）⇔2），2）⇔3）显然.

2）⇒4）设 D是 x的 Zc-极小集，则 D∈Zc（P），x＝∨D，D⊆⇓Zcx.由连通集系统 Zc的定义及 f保 Zc-集的并知↓f（D）∈Zc（P），∨↓f（D）＝∨f（D）＝f（∨D）＝f（x），且 f（D）⊆f（⇓Zcx）⊆⇓Zcf（x），故↓f（D）⊆⇓Zcf（x）.由推论2.5 知↓f（D）是 f（x）的 Zc-极小集.

4）⇒5）设 D∈Zc（P），d＝∨D.由 f保序知∨f（D）≤f（d）.反之，∀x∈⇓Zcd 即 x≪Zcd，∃a∈D，使得x≤a，从而 f（x）≤f（a）≤∨f（D），f（⇓Zcd）≤∨f（D）.由4）知↓f（⇓Zcd）是 f（d）的 Zc-极小集，则f（d）＝∨↓f（⇓Zcd）＝f（⇓Zcd），故 f（d）≤∨f（D），即f保 Zc-集的并.∀x∈P，由推论2.5 及↓f（⇓Zcx）是f（x）的 Zc-极小集知

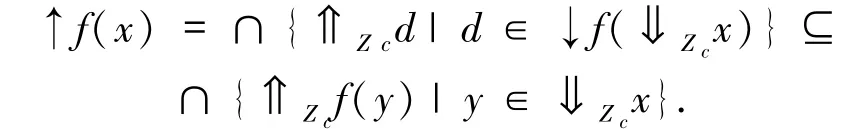
5）⇒1）设 a≪Zcb即 a∈⇓Zcb.由↑f（b）⊆∩｛⇑Zcf（y）｜y∈⇓Zcb｝知↑f（b）⊆⇑Zcf（a），从而f（b）⊆⇑Zcf（a），即 f（a）≪Zcf（b）.

定义3.6设P是Zc-完备的偏序集，B⊆P.若∀x∈P，⇓Zcx∩B∈Zc（B）且∨（⇓Zcx∩B）＝x，则称B是P的一个Zc-基.

定理3.7（扩张定理）设Zc是并完备的连通集系统，P，Q是Zc-连续偏序集，B是P的Zc-基.若g：B→Q是保Zc-集的并且保≪Zc的映射，则g可扩张为一个保Zc-集的并且保≪Zc的映射f：P→Q，且扩张是唯一的.

证明∀x∈P，令 f（x）＝∨↓g（⇓Zcx∩B）＝∨g（⇓Zcx∩B），下证f是满足条件的扩张.

1）x∈B 时，f（x）＝∨g（⇓Zcx∩B）＝g（∨（⇓Zcx∩B））＝g（x）.

2）若 a≤b，则⇓Zca∩B⊆⇓Zcb∩B.从而g（⇓Zca∩B）⊆g（⇓Zcb∩B），f（a）≤f（b）.即 f保序.

3）设 D∈Zc（P），d＝∨D.由 f保序知∨f（D）≤f（d）.反之，∀x∈⇓Zcd∩B，由 x≪Zcd 知∃a∈D，使得 x≤a.从而 g（x）＝f（x）≤f（a）≤∨f（D），故 f（d）＝∨g（⇓Zcx∩B）≤∨f（D）.即 f保Zc-集的并.

4）设 a，b∈P，a≪Zcb.由引理 2.6 知∃c∈P，a≪Zcc≪Zcb.由于 B 是 P 的 Zc-基，则∨（⇓Zcb∩B）＝b.从而∃u∈⇓Zcb∩B，使得 a≪Zcc≤u≪Zcb，故 a≪Zcu≪Zcb.同 理 可 得 ∃v∈ B，使 得a≪Zcu≪Zcv≪Zcb.由 f保序及 g 保≪Zc知 f（a）≤f（u）＝g（u）≪Zcg（v），故 f（a）≪Zcg（v）.又由 f的定义知g（v）≤f（b），所以 f（a）≪Zcf（b），即 f保≪Zc.

5）设h：P→Q是g的另一个满足条件的扩张.则∀x∈ P，h（x）＝h（∨ （↓ （⇓Zcx∩ B）））＝∨h（↓（⇓Zcx∩B））＝∨↓h（⇓Zcx∩B）＝∨h（⇓Zcx∩B）＝∨g（⇓Zcx∩B）＝f（x）.即扩张是唯一的.

注3.8Zc-基B关于P上的序未必是Zc-完备偏序集.g：B→Q保Zc-集的并是指若∀S∈Zc（B），∨S∈B，则 g（∨BS）＝∨Qg（S）.故在定义3.6 中要求⇓Zcx∩B∈Zc（B）.