基于有限元的钢爪摩擦焊机床身结构设计及优化研究*
2018-03-15李权飞兰州理工大学机电工程学院甘肃兰州730050
王 斌,辛 舟,李权飞(兰州理工大学 机电工程学院,甘肃 兰州 730050)
0 引 言
摩擦焊机是由摩擦焊主机、液压系统、电气控制系统三部分组成。其中,摩擦焊主机是由机身、主轴箱、顶端装置、4根导柱、夹具、电机等组成。
钢爪摩擦焊机在摩擦焊接过程中,顶端压力、摩擦压力、摩擦扭矩通过钢爪本体夹具传到床身上。因此,床身的强度、刚度及稳定性要求较高,如果床身变形过大,不仅会使床身上的夹具出现爬行现象,而且还会引起系统的严重振动。床身作为钢爪摩擦焊机非常重要的基础件,关系到零件的焊接质量以及机床的工作寿命[1-3]。因此,床身的强度,刚度及稳定性要求较高。而床身的静动态特性直接影响着钢爪摩擦焊机的工作性能。钢爪摩擦焊机在焊接过程中需要3 500 kN的顶锻压力以及32 000 N/m的扭矩,因此,要求床身结构应具有较好的静动态性能。
本文通过Solidworks建立钢爪摩擦焊机床身模型,导入ANSYSWorkbench中进行静动态分析以及灵敏度分析,根据灵敏度分析结果改进床身结构,进而增加床身静、动态性能,改善焊接质量,减小床身质量。
1 灵敏度理论分析
灵敏度分析是指结构的特征参数对结构的物理参数(质量、刚度、阻尼)的变化率。通过灵敏度分析,可以掌握结构各部分的参数变化与特征变量的敏感程度,为结构优化提供方向[4]。
无阻尼的特征方程为:
(1)
式中:[M]—质量矩阵;[K]—刚度系数;[ωr]—第r阶固有频率;[φr]—第r阶模态振型。
将式(1)左乘,并求对变量μ求偏导,可得:
(2)
将式(2)化简可得动态特性灵敏度公式:
(3)
式中:μ—M、K矩阵中任意元素,因而可以通过改变其结构参数进而改变其特征参数。
这里将以床身的厚度以及肋板的厚度作为设计变量,通过灵敏度分析进而改进床身结构。
2 床身初步结构设计及建立模型
本研究根据钢爪摩擦焊机的加工工艺要求以及参考其他机床床身机构,初步设计出钢爪摩擦焊机床身结构[5-6]。
笔者用Solidworks对其进行三维建模,床身模型如图1所示。

图1 床身三维模型P1—床身大端板;P2—外纵立板;P3—内纵立板(上);P4—内纵立板(下);P5—底板;P6—中间面板;P7—上面板;P8—上肋板;P9—下肋板
初步设计床身的各壁板厚度及肋板的厚度均为t=30 mm。
3 床身有限元分析
3.1 将初步设计的床身进行静态分析
本研究用Solidworks建立初步设计床身的三维模型,然后导入ANSYSWorkbench中进行静态分析[7]。
床身的各项参数如下:
材料为16Mn;
泊松比为u=0.31;
弹性模量E=212 GPa;
屈服强度为345 MPa;
床身质量为20 571 kg。
本研究在床身的16个地脚板处施加固定约束,约束其所有自由度。由于床身结构较为复杂且倒角多,本研究对床身模型采用自由网格划分,划分出60 607个节点,20 667个单元[8]。
床身的应力云图如图2所示。

图2 床身的应力云图
床身的最大应力为152.47 MPa,出现在中间面板与4根导柱连接处。由于材料的屈服强度为345 MPa,满足强度要求。
床身的综合变形图如图3所示。

图3 床身的综合变形图
床身的最大综合变形为0.480 33 mm,床身的最大变形较大,影响加工质量,因此要通过改变壁厚、肋板的厚度以及肋板的分布进而减小床身的总变形。床身的最大变形在4根导柱与中间面板连接处,且出现应力集中现象。
因此,为了减小在此处的应力应变,改变其肋板分布。
改变后的肋板分布如图4所示。

图4 床身内部肋板分布图
3.2 床身壁板厚度与肋板厚度灵敏度分析
本研究以壁厚、肋板的厚度与位置等参数为设计变量进行灵敏度分析,以床身的总变形大小作为衡量床身静态性能的主要参数,得到各个变量对床身最大变形的影响程度,在此基础上改变各个变量进而减小床身的综合变形,最终改善床身静态性能。文献[9]对床身的灵敏度分析及结构优化提供了可靠的参考与理论依据。
板厚对床身的最大变形灵敏度由床身的壁厚、肋板的厚度对床身最大变形的影响程度得到,如图5所示。
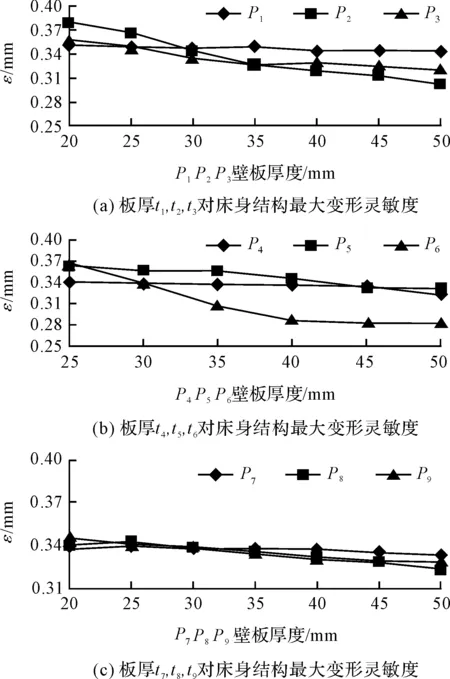
图5 各壁板厚度对床身最大变形灵敏度
从图5(a)可以看出:随着床身两侧大端板(P1)厚度t1的增加,床身的总变形基本保持不变,考虑到床身的重量,取其厚度t1=20 mm。外纵立板(P2)随着壁厚t2的增加床身最大变形逐渐减小,因此取P2的壁厚t2=50 mm。将内纵立板(上)的壁厚增加到35 mm后,床身的最大变形基本保持不变,因此可取内纵立板(上)(P3)的厚度t3=35 mm。
从图5(b)可以看出:内纵立板(下)(P4)随着其壁厚的增加床身最大变形几乎没有变化,因此取其壁厚t4=30 mm。底板(P5)随着壁厚增加到45 mm后床身最大变形基本保持不变,取t5=45 mm。中间面板(P6)壁厚增加到40 mm以后床身最大变形基本保持不变,所以取t6=40 mm。
从图5(c)可以看出:上面板(P7)壁厚增加到30 mm后床身的最大变形基本保持不变,因此取其壁厚t7=30 mm。增加上肋板(P8)壁厚床身最大变形逐渐减小,因此取其壁厚t8=50 mm。增加下肋板(P9)的壁厚床身变形也逐渐变小,取其壁厚t9=50 mm。
床身各壁板厚度如表1所示。

表1 床身各壁板厚度
3.3 将改进后的床身进行静态分析
本研究将改进后的床身用Solidworks建立的三维模型导入ANSYSWorkbench中进行静态分析。
床身等效应力云图如图6所示。

图6 床身应力云图
床身的最大应力145.91 MPa,小于初步设计床身的最大应力152.47 MPa,小于屈服强度345 MPa,因此改进后的床身满足强度要求。
床身的综合变形图如图(7,8)所示。

图7 床身综合变形图

图8 床身内部综合变形图
可见:最大变形在中间面板与导柱连接处,改进后床身的最大变形为0.172 13 mm,远小于初步设计的床身的最大变形0.480 03 mm。
4 床身模态分析
床身可以简化成一个多自由度系统。多自由度系统无阻尼自由振动运动方程为:

(4)

设方程的解为:
{x}={A}eiωnt
(5)
式中:{A}—系统左右振动时的振幅向量。
将式(2)代入式(1)可得:
(6)
当{A}的系数矩阵为零时,即:
(7)
上式称为特征方程。n个自由度系统有n个固有频率和n个主振型。由于床身上的激振力的频率都不高,只有最低的固有频率可能与激振频率接近或重合,只需对床身的低阶模态进行分析。
在结构的动态分析中,各阶模态所具有的权重因子大小与该模态频率的倒数成正比,也就是说低阶模态特性基本决定了产品的动态特性[10]。
将床身进行模态分析,确定其1阶模态。1阶模态振型如图9所示。

图9 床身1阶模态
由图9可知,床身结构有较强的抗弯和抗扭能力。床身的一阶固有频率为148.19 Hz,远大于床身工作时的最大频率50 Hz,因此钢爪摩擦焊机在工作时床身不易发生共振。
5 结束语
本研究将初步设计的钢爪摩擦焊机床身模型导入ANSYS Workbench中进行静态分析,得到其最大变形0.480 03 mm,最大应力152.47 MPa。通过灵敏度分析,将床身及肋板厚度作为设计变量,通过改变壁板厚度及肋板厚度来减小床身的最大变形,最终得到床身的最大变形为0.172 13 mm,最大应力为145.91 MPa,相比较初步设计床身的静态性能,通过优化的床身静态性能得到很大改善。最后将优化的床身进行模态分析,得到床身的最大频率为148.19 Hz,远大于床身的固有频率,得到其床身有较好的抗弯和抗扭刚度。
研究结果可为大吨位、大扭矩机床床身的设计与优化提供参考。
[1] 刘 江,唐传军.立式加工中心床身结构有限元分析与优化[J].组合机床与自动化加工技术,2010(4):20-22.
[2] 吴良宝,张年松,张 立.CK1440型数控车床床身动态特性分析[J].机械制造与自动化,2011(6):18-19.
[3] 李和明.基于ANSYSY Workbench数控铣床床身的静模态分析[J].现代制造技术与装备,2014(6):23-25.
[4] 何成浩,尹志宏.基于有限元分析的机床床身结构优化设计[J].科学技术与工程,2012(12):5743-5746.
[5] 王艳辉,伍建国.精密机床床身结构参数的优化设计[J].机械设计与研究,2003(6):53-55.
[6] 杨志冬,赵 晨,张卫园.稀有金属粉体称量机振动给料器运行参数的正交优化[J].包装与食品机械,2016(3):1-4.
[7] 许京荆.ANSYS Workbench工程实例[M].北京:人民邮电出版社,2015.
[8] 杜 勇,辛 舟.5 000 kN连续驱动摩擦焊机主轴箱的有限元分析[J].机械设计,2014(7):51-53.
[9] 李建福.灵敏度分析方法及其在机械优化设计中的应用[D].烟台:烟台大学机电汽车工程学院,2010.
[10] 汤文成,易 红,幸 研.加工中心床身结构分析[J].机械强度,1998(3):11-13.
