基于模糊PID的送杆机构同步控制建模与仿真研究*

周 围，李群明,2,3，高志伟，谢 帅

(1.中南大学 机电工程学院，湖南 长沙 410083; 2.中南大学 轻合金研究院，湖南 长沙 410083; 3.中南大学 高性能复杂制造国家重点实验室，湖南 长沙 410083)

0 引 言

某课题组所设计的岩心取样钻机用送杆机构主要用于输送杆件到固定位置，辅助钻机完成自动接杆操作。其中，送杆机构的送杆过程由对称安装的两个运送油缸驱动。为保障送杆过程平稳、位置精确，需要实现两缸多点位精度同步控制，且误差应小于1 mm。

为了提高系统的同步控制精度，相关学者做了大量研究。许勇[1]指出了液压同步控制主要有“同等方式”和“主从方式”，而“主从方式”因从动系统输出跟踪主动系统具有延时性，会出现较大的动态同步误差；针对回收机扫油臂与卷筒双马达同步控制问题，杨前明等[2]提出了一种“同等控制”结合模糊神经网络的同步控制器，系统同步精度高、无超调；针对锻造机双缸同步提升系统，吴娜等[3]提出了一种单神经元PID和交叉耦合的同步控制算法，系统的收敛性快、鲁棒性好；针对非对称液压缸与负载形成运动闭链而导致力耦合问题，窦海斌[4]设计出了一种鲁棒自适应跟踪控制器；针对多缸组成的同步提升系统，DONG Li-jing等[5]提出了一种大型举升系统的分布式控制策略，通过各缸的分布式控制器达到了耦合同步；针对提升装置同步误差对盾构管片拼装质量的影响，彭雄斌等[6]提出了一种双比例阀模糊PID控制方法，提高了两缸同步精度；针对海洋工程中大型结构块对接的多缸同步问题，成思铭等[7]提出了一种多缸耦合的模糊PID控制方法，避免了系统加减速的同步波动；针对拉床中两缸卧室电液同步系统具有线性和非线性级联问题，CHEN Guo-jin[8]等提出了一种IPSO-PID同步控制器，并引入了改进型粒子群优化算法。

上述方法虽然可实现两缸精确同步控制，但存在建模和控制算法复杂、工程实用性差等问题，难以满足送杆机构的实际需求。

针对上述不足，笔者提出送杆机构的送杆过程同步控制方案，并通过同等方式建立送杆过程数学模型和两缸闭环同步控制系统模型，然后设计模糊PID控制器，利用MATLAB的Simulink模块进行仿真分析，得到送杆过程的同步特性，验证控制方案的合理性。

1 送杆机构工作原理

送杆机构如图1所示。

图1 送杆机构图1—机架；2—运送油缸；3—支架安装架；4—运送支架；4.1—套管卡槽；4.2—钻杆卡槽；5—储杆箱；5.1—钻杆容纳腔；5.2—套管容纳腔；6—钻杆；7—套管

图1中，送杆机构的运送油缸推动运送支架进行钻杆或套管的选取或归位输送时，需要保障运送支架的钻杆卡槽或套管卡槽精确地对准储杆箱的钻杆容纳腔或套管容纳腔，进而才能精确地选取所需钻杆或套管。

由于送杆机构采用两边对称安装的运送油缸分别驱动两边的运送支架，而运送油缸的进油流量、油缸泄露、负载力耦合等因素会导致其活塞杆伸出行程难以同步，两边运送支架的卡槽中心线与储杆箱中杆件的中心线存在偏角，导致杆件不能精确落到卡槽内，使送杆机构不能正常工作。

2 送杆过程闭环同步控制系统建模

送杆机构的送杆过程模型如图2所示。

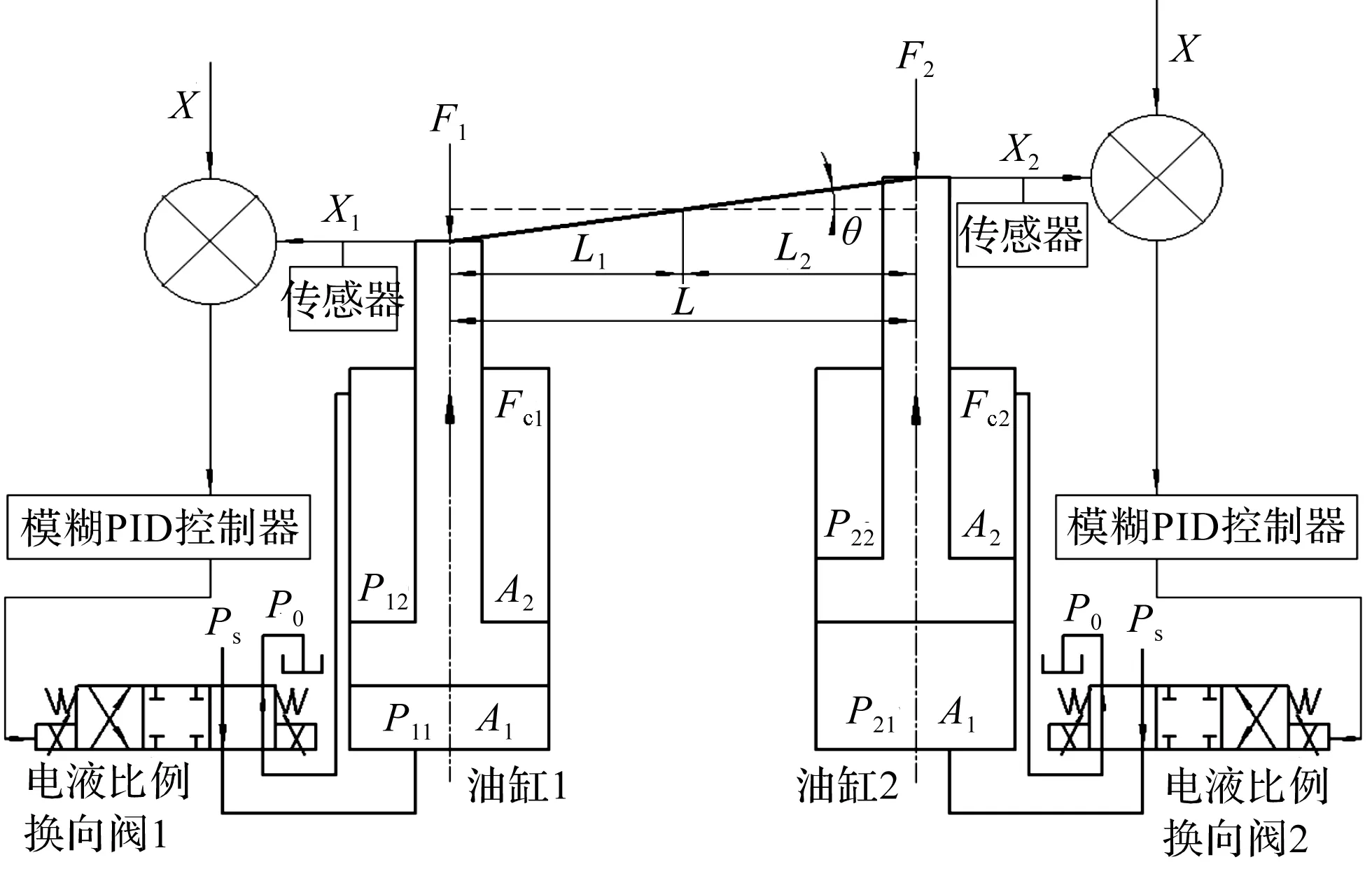
图2 送杆机构的送杆过程模型图

图2中，控制信号为运送油缸活塞杆伸出的理论位移或速度，油缸可通过位移传感器实时检测并反馈实际位移，然后将理论位移与实际位移的误差和误差变化率，作为模糊PID控制器的输入信号，再通过模糊PID控制器输出控制电压信号，调节电液比例换向阀的阀芯开度大小，进而调节运送油缸的流量与压力，达到对送杆过程实现闭环同步控制的目的。

2.1 两缸输送杆件的同步控制动力学模型

(1)两缸实际位移与杆件偏转方程为：

(1)

式中：θ—杆件的偏转角度；X1—油缸1实际位移；X2—油缸2实际位移；L—两缸中心距。

(2)运送支架与杆件的平面运动方程为:

(2)

(3)

(4)

式中：FC1，FC2—油缸1和油缸2的输出力；F1，F2—两边运送支架受到的摩擦阻力；M1—杆件质量；M2—运送支架质量；J1—杆件转动惯量；Y—杆件质心实际位移；L1，L2—杆件质心到油缸1或油缸2的中心距。

由式(1～4)可得：

(5)

(6)

2.2 电液比例换向阀数学模型

(1)比例电磁铁输出力方程为：

FD=KuU

(7)

式中：Ku—比例电磁铁电压力增益；U—比例电磁铁输入电压；FD—电磁铁输出力。

(2)比例电磁铁力平衡方程[9]为：

(8)

式中：mD—阀芯等效质量；cD—阀芯综合阻尼系数；kD—阀芯弹簧刚度；XV—电磁铁阀芯位移。

由式(7～8)可得，电磁铁阀芯位移方程为：

(9)

2.3 对称阀控制非对称缸数学模型

笔者以电液比例换向阀1控制油缸1为例来进行建模[10]。

2.3.1 阀1负载压力与负载流量的定义

稳态下油缸1力平衡方程为：

P11A1-P12A2=FC1

(10)

稳态下油缸1流量方程为：

(11)

稳态下油缸1输出功率方程为：

P11Q1-P12Q2=W

(12)

式中：P11，P12—油缸1无杆腔压力和有杆腔压力；A1，A2—油缸1无杆腔面积和有杆腔面积；Q1—流入或流出油缸1无杆腔流量；Q2—流出或流入油缸1有杆腔流量；W—液压缸输出功率。

由式(10～12)可得：

阀1负载压力为：

(13)

阀1负载流量为：

(14)

2.3.2 电液比例换向阀1的阀口流量方程

(1)正向XV1≥0时：

(15)

(16)

式中：Cd—阀的流量系数；ω—阀口面积梯度；XV1—换向阀1的阀芯位移；ρ—液压油密度；PS—系统压力；P0—回油压力。

由式(11，15，16)可得：

(17)

由式(13，17)可得：

(18)

(19)

由式(14，15，18)可得正向负载流量：

(20)

(2)反向XV1<0时：

(21)

(22)

同理，可得反向负载流量：

(23)

(3)阀1的压力流量特性方程为[11]：

由式(20，23)可得：

QL=KqXV1-KcPL

(24)

(25)

(26)

式中：Kq—流量增益系数；Kc—流量压力系数。

2.3.3 油缸1的流量连续性方程

(1)无杆腔流量：

(27)

(2)有杆腔流量：

(28)

式中：Cip—油缸内泄露系数；Cep—油缸外泄露系数；V1—油缸无杆腔容积；V2—油缸有杆腔容积；βe—油液体积弹性模量。

由式(27～28)可得负载流量[12]：

(29)

代入上式正反向P11、P12可得：

(30)

(31)

(32)

(33)

式中：Cap—附加泄露系数；Cbp—等效泄露系数；Ve—等效容积。

2.3.4 油缸1的力平衡方程

力平衡方程为：

(34)

式中：M—折算到活塞杆上的总质量；Bp—负载粘性阻尼系数；Kf—负载弹簧等效刚度。

由于送杆机构采用相同型号的力士乐电液比例换向阀驱动同种型号的油缸，可根据式(5，6，9，24，30，34)分别建立送杆过程的两缸闭环同步控制系统模型。

送杆过程两缸闭环同步控制系统模型如图3所示。

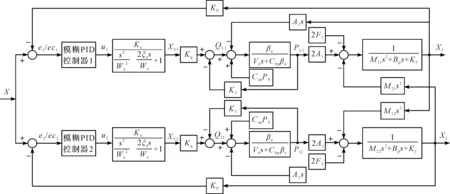
图3 送杆过程两缸闭环同步控制系统模型图

反馈系统采用磁致伸缩位移传感器，可直接检测并反馈油缸实际位移的绝对值，其中：KP—传感器反馈系数。

根据图3有：

(35)

3 模糊PID控制器设计与仿真分析

3.1 模糊PID控制器设计

由于控制系统具有强耦合和模型参数不确定性的特点，采用模糊PID控制能够提高控制精度和抗干扰能力。

笔者利用Simulink建立模糊PID控制器，以油缸的理论位移与实际位移的误差量e和误差变化率ec为输入，通过模糊控制器输出参数Δkp、Δki、Δkd，整定PID控制中的KP、KI、KD参数，从而使得模糊PID控制器能够精确地调节阀芯的开度大小。

设定系统误差量e和误差变化率ec的基本论域为[-1，1]，模糊输出量Δkp、Δki、Δkd的基本论域为[-6，6]；系统误差量e、误差变化率ec和模糊输出量Δkp、Δki、Δkd离散论域均为{-6，-5，-4，-3，-2，-1，0，1，2，3，4，5，6}；各变量的模糊子集设为{NB、NM、NS、ZO、PS、PM、PB}，分别对应{负大、负中、负小、零、正小、正中、正大}。

在MATLAB的fuzzy工具箱中，编辑输入量和输出量均采用三角形隶属度函数；解模糊选取重心法。

模糊控制器参数的在线整定过程，就是找到输入量e、ec和输出量Δkp、Δki、Δkd之间的模糊关系。

根据工程实践经验，可得到如下的模糊控制规则[13-14]：

(1)当|e|较大时，为提高系统响应速度，取较大的Δkp，取较小的Δki、Δkd，防止系统过度超调；

(2)当|e|适中时，为减小系统超调量，取较小的Δkp，取适当的Δki、Δkd，保障系统的响应速度；

(3)当|e|较小时，为使系统稳定，取较大的Δkp、Δki，取适当的Δkd，减小系统静差；

(4)当|ec|较大时，Δkd取值应越小，当|ec|较小时，Δkd取值应越大，避免系统振荡。

Δkp的模糊规则如表1所示。

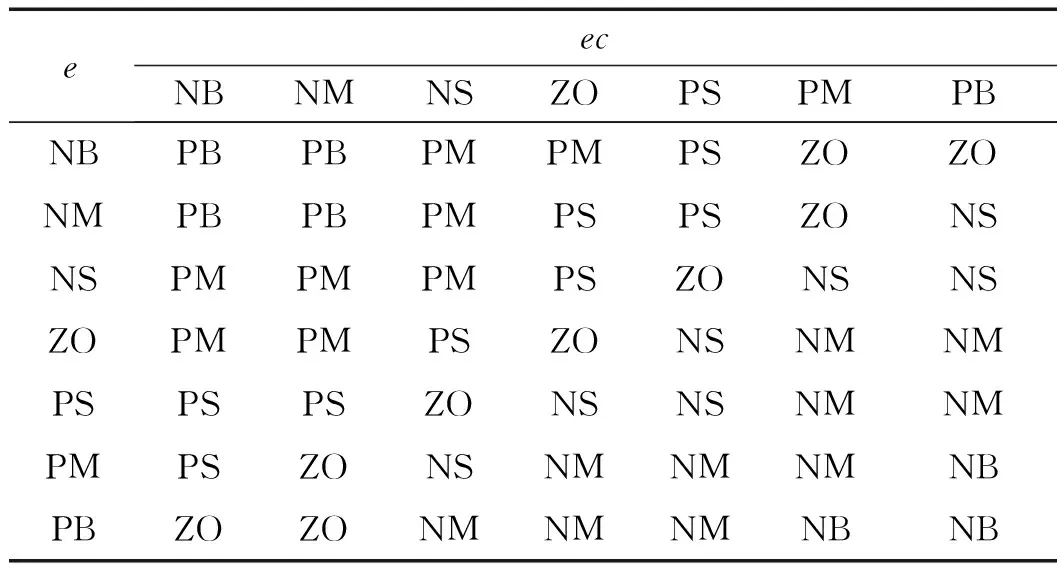
表1 Δkp的模糊规则表

Δki的模糊规则如表2所示。

表2 Δki的模糊规则表

Δkd的模糊规则如表3所示。

表3 Δkd的模糊规则表

根据以上模糊规则，笔者在模糊推理系统中，通过模糊语言(If e is ... and ec is ..., Then Δkpis ... and Δkiis ... and Δkdis ...)进行模糊规则编辑，共有49条模糊语言。

3.2 仿真分析

根据前文送杆过程两缸闭环同步控制系统模型，笔者利用Simulink进行仿真分析。

控制系统主要仿真参数如表4所示。

在输送杆件过程中，送杆机构需要实现两缸多点位精度同步控制，且最小定位位移是65 mm，最大定位位移是670 mm。为避免油缸在启动和停止时速度突变，造成液压冲击，笔者在仿真中采用速度控制信号。

油缸速度控制信号如图4所示。

表4 控制系统主要仿真参数表

图4 油缸速度控制信号图

图4中，速度信号为先匀加速，再匀速，最后匀减速的过程；且低速为0.05 m/s，高速为0.2 m/s。在此基础上，从而可以对不同速度控制下的两缸同步误差进行对比分析。

低速时两缸同步误差如图5所示。

图5 低速时两缸同步误差图

图5中，油缸以0.05 m/s低速实现最小位移65 mm精确定位时，对比传统PID控制器和模糊PID控制器的控制效果可见，油缸的速度和位移能够较好地跟踪控制信号；其中，采用传统PID时，两缸的最大同步误差有0.13 mm，稳定时的最终误差有0.05 mm；而采用模糊PID时，两缸的最大同步误差只有0.09 mm，稳定时的最终误差只有0.02 mm。

高速时两缸同步误差如图6所示。

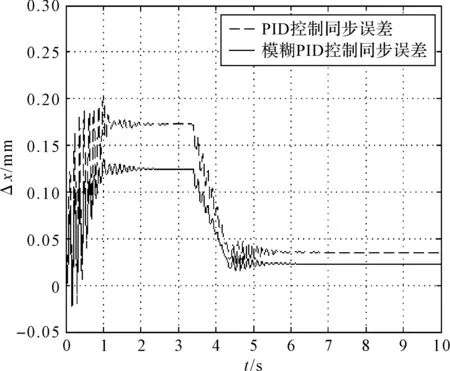
图6 高速时两缸同步误差图

图6中，油缸以0.2 m/s高速实现最大位移670 mm精确定位时，采用传统PID时，两缸的最大同步误差有0.20 mm，稳定时的最终误差有0.04 mm；而采用模糊PID时，两缸的最大同步误差只有0.13 mm，稳定时的最终误差只有0.03 mm。

从图(5，6)可得：在油缸匀加速启动时,采用同等控制方式时，在加速度的影响下，控制系统的同步误差逐渐增大；但在油缸匀减速停止时,系统会加快对同步误差的调节作用。

综上所述，与传统PID控制相比较,模糊PID控制能够较大地提高系统的控制精度。

4 结束语

(1)以某课题组所设计的钻机用送杆机构为例，笔者分析了送杆机构因同步误差不能正常工作的原因，并通过同等方式建立了送杆机构的送杆过程数学模型和两缸闭环同步控制系统模型；

(2)设计了模糊PID控制器，利用MATLAB的Simulink模块进行了仿真分析，并与传统PID控制进行了控制效果的对比。对比结果表明：模糊PID控制系统工作稳定、响应速度快、同步精度高，油缸能够较好跟踪控制速度和位移信号，低速时最大同步误差只有0.09 mm，高速时最大同步误差只有0.13 mm，满足送杆机构的同步控制需求；

(3)采用的模糊PID同步控制方法，不仅适用于两缸同步系统，而且适用于工程上的多缸同步系统，其控制系统的控制算法简单、搭建成本低，具有一定的借鉴价值。