格构锚杆边坡支护结构稳定性计算方法

2020-09-22曾承晶

建材与装饰 2020年26期

关键词：格构圆弧圆心

曾承晶

（贵州省建筑设计研究院有限责任公司，贵州贵阳 550081）

0 前言

格构锚杆为一种常用的支护结构，可以将其应用于大规模土质边坡支护工作中。因此，有必要探究边坡稳定性计算方式，建立满足土体土坡支护结构稳定性的模型，找寻提升锚杆支护结构稳定性的方式，提高框架支护结构设计水平，进而提高项目施工安全性和质量。

1 格构锚杆模型分析

格构锚杆边坡支护结构是轻质挡土类型，包含墙后土体、框架和锚杆等结构[1]，框架中还包括挡土板、竖梁和横梁，结构受力形式和竖向梁板结构类似。锚杆锚头一般设置在横梁与竖梁交接处，其锚固段锚入需加固的土体当中，锚杆受力时的工作机理如下：锚杆→锚固段砂浆→土体与砂浆摩擦力→锚固区地层。通过上述力的传递可以将下滑力或土压力传递至稳定土层中，其结构立面图如图1所示。

图1 支护结构立面

格构锚杆中的横梁和竖梁可按支撑与于弹性锚杆的连续梁进行设计和内力计算；根据挡土板与横梁和竖梁连接构造的不同，可简化为支撑在梁上的水平连续板、简支板或双铰拱板进行设计和内力计算。

2 稳定性计算模式分析

2.1 安全系数

分析边坡破坏情况是研究边坡稳定性的基础，可以体现出边坡破坏机理和形态。边坡破坏形式包含平面破坏、圆弧破坏、混合破坏模式，分析其稳定性需要结合破坏机理和形态，依据荷载条件、工程条件、支护情况分析其受力平衡状态[2]。通过引入极限平衡理论，完成对格构锚杆支护结构的受力平衡计算。因此，应分析土体力学指标、预应力作用。若边坡破坏情况是圆弧滑动模式，稳定性计算需侧重土体滑移力对于滑动面的影响，使得土体作出圆弧滑动。在检验边坡支护结构内部稳定性时，需明确边坡倾角、高度、滑移面半径、结构下端水平推力对于滑动体的荷载，土体粘聚力、土体自重与地面附加荷载等数据。其中，分析边坡稳定性主要是为了寻找契合静力平衡的标准与安全系数，求出最低安全系数，其数值可用Ks表示。

边坡内部稳定性的安全系数计算公式是：Ks=（Fs1+Fs2+Fs3+△Fs）/F。在该式子中△Fs是锚杆预应力对土体稳定性产生的影响效应，需要将其作为安全储备因素进行分析[3]。该公式中Fs1、Fs2、Fs3分别为土地粘聚力所形成的抗滑移力、坡顶地面和土体自重荷载的产生的抗滑移力、锚杆的抗滑移力。

2.2 圆弧滑动方式

该方式适用于土质边坡，当确定滑移面后，其边坡稳定性计算公式为：Ks=MR/MT。Ks是边坡的实际稳定性系数；MR与MT为滑动面中抗滑力矩和下滑力矩，可分别按下式计算：

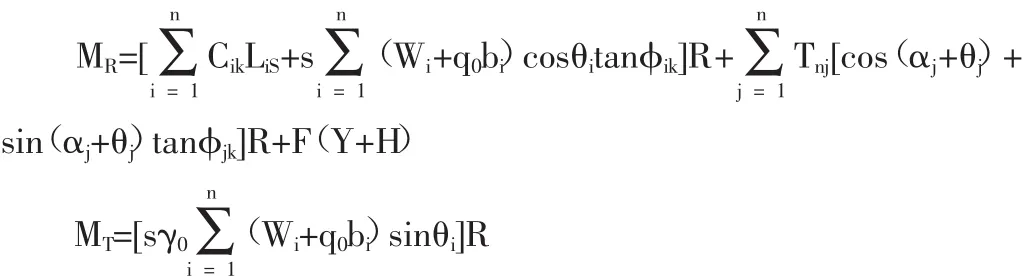
式中：H-边坡支护高度；bi-第i分Α条的实际宽度；θi-滑裂面水平面和切线间夹角；q0-顶面荷载的实际分布情况；m-锚杆层数；n-滑动体的实际分条数；Ls-滑裂面位置的弧长；F-锚杆底端水平推力数值；φik-摩擦角数值；αj-锚杆和水平面夹角；Wi-第i个分条土的重量；R-抗滑面上圆弧的实际半径；0-重要性系数；s-滑动体单元的实际厚度；Cik是第i条滑裂面粘聚力值；Y-圆心到地表距离。

2.3 圆弧滑动分条

借助圆弧滑动分条的方式可以计算边坡稳定性，当明确滑移面后能够得到稳定性系数。在使用此模式时应确定危险滑移面，得出最低安全系数，再结合该数值分析边坡的实际稳定性能否满足标准，计算过程如下：

2.3.1 假设阶段

假设圆心不在直线OE下侧与直线OC右侧的可能性是0，结合几何关系可以得出圆弧中水平面和切线的夹角是0°～90°。边坡滑移面最危险圆弧经过基坑角点A，实际情况如图2所示。

图2 滑移面模型

2.3.2 构建滑移面搜索模型

以图 2 为例，将 O′作为圆心，O（0，0）当作坐标原点，构建直角坐标系。O′所处位置位于矩形OCDE，将R当作圆弧的半径。在构建搜索模型时，结合圆心的实际位置获取滑移面，计算其稳定性系数。在该坐标系内，变量计算方式如下：若第j层的锚杆和圆弧交点作为中心C，则滑移内部锚杆长度用Ifj表示，外部长度是Inj，因此总长度计算公式是Lj=Ifj+Inj。

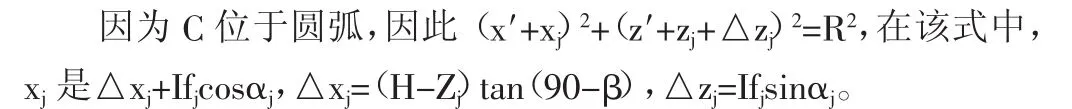
式中：H-开挖的深度；β-水平面和边坡的夹角；zj-第j根锚杆的端头至地面的实际距离；lfi可以借助迭代的方式设置定步长（△lfi），当第n次迭代后，公式为lfi=n△lfi。因此，锚杆总长可以作为稳定性验算中的质量，lnj和lfj实际上是锚固段和自由端的长度。同时，自由段设计时其长度需超过计算长度，确保该部分能够快速穿过滑移体至稳定土层内，该部分长度可以适当增加，进而提升锚固力。

2.3.3 计算第i条土的重量

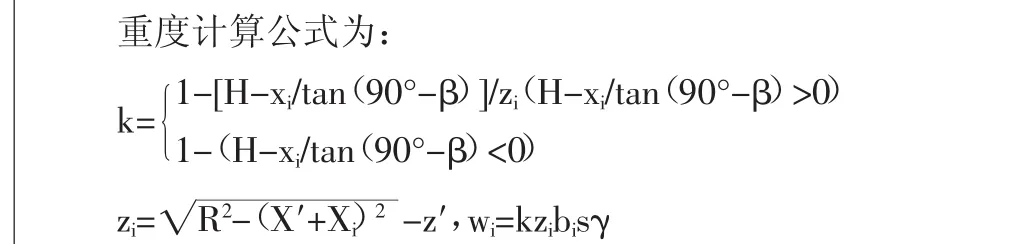
式中：k-边坡分条土重量的实际计算系数；zi-原点到第i条带底部中点的竖向距离；xi-水平距离。

2.3.4 定位最危险滑移面的圆心

当确定某一圆心后，结合力矩极限平衡理论，可以获取圆弧实际安全系数，即K。矩形OCDE圆心位置，借助网格法可以将其划分为数量是n×n的圆心，进而在其中找寻最低安全系数，将其设置为最危险的滑移面圆心。

2.4 稳定性计算总结

①基于极限平衡理论，可以借助积分的方式构建最危险滑移面搜索模型、稳定性安全系数模型，分析安全系数和滑移面圆心的函数关系。通过网格法得到安全系数；②探究锚杆因素对于土体稳定性的影响，得到圆心搜索区域内边坡设计参数的变化值；③对于土质良好的边坡，可以通过构建最危险滑移面模型计算稳定性；若土质边坡较差或边坡破坏情况较为复杂，则很难确定圆心搜索位置，应结合相关数值进行工程设计；④引入推导框架思想，对滑坡治理和土坡稳定性完成精准控制。在计算中需要充分考虑土体参数、施工概况、锚杆局部情况等因素对于边坡土体稳定性的影响。