关系诱导的形态学算子及其性质

戴乐君， 胡碧玉， 何祎宁， 苏郇立

（苏州科技大学 数理学院，江苏 苏州215009）

数学形态学是以集合论、格论、积分几何等为严格数学基础的交叉性学科，由法国的J.Serra 和Matheron于1964年提出。近几十年数学形态学得到了快速的发展，在法国、瑞典等国家一直有许多学者（如C.Ronse，P.Soille）和研究团队（如法国的丹枫白露、英格兰的Silsore 研究院）在进行数学形态学的研究和应用开发，出现了许多有意义的工作，如C.Kiselman[1]、I.Bloch[2]、郭艳艳[3]等人的有关研究。数学形态学广泛应用于信号、图像分析和处理、模式识别等领域，是一个发展前景广阔的领域。 数学形态学的研究大多集中在具体应用和算法的探讨上，近年来越来越多的数学家开始形态学的研究，使得数学形态学的理论基础逐步完善，例如，格上形态学[4-6]、度量空间上形态学[7-9]、模糊形态学[10]、随机形态学、数字几何空间拓扑理论等。 这些理论的建立一方面为形态学的应用提供了更多的方法和理论指导，同时也促进了理论数学研究的深入和新的数学理论的产生[11]。笔者利用集合X 上的关系给出其幂集上膨胀和腐蚀算子的定义；讨论由关系诱导的形态学算子的基本性质；探讨了关系的性质和其诱导的形态学算子性质之间的联系，并由此定义了膨胀的上确界和下确界运算，指出幂集P（X）上的所有膨胀算子构成一个完备格。

1 由关系诱导的膨胀和腐蚀及基本性质

文中，X 为非空集合，R 为X 上的关系，即R⊂X×X。 首先，给出P（X）上由R 诱导的膨胀和腐蚀算子，为了方便起见，除非特别说明，文中X 均为非空集合，P（X）为X 的幂集，R 为X 上的关系，即R⊂X×X。

定义1[1]设δ:P（X）→P（X），若δ∪i∈ΛAi=∪i∈ΛδAi，则称δ 为膨胀；若ε∩i∈ΛAi=∩i∈ΛεAi，则称ε 为腐蚀。

定义2设R 为X 上的关系，定义算子δ，ε:P（X）→P（X）如下：

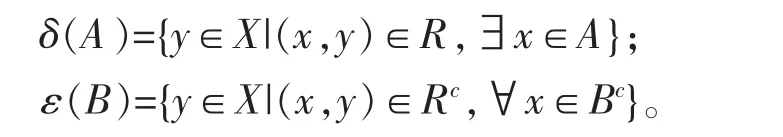
其中，Rc表示R 的补关系。

注1如果A=Ø 或者对任意x∈A 不存在y∈X 使得（x，y）∈R，则δ（A）=Ø；若B=X，则ε（B）=X；若R=Ø，则约定δ（A）=Ø。

定理1由定义2 中给出的算子δ，ε 分别为膨胀和腐蚀，且（ε，δ）是一对附益算子，即δ（A）≤B⇔A≤ε（B）。

证明首先，对y∈δ∪（Ai），存在x∈∪（Ai）使得（x，y）∈R，于是存在Ai满足x∈Ai。 于是y∈δ（Ai）⊂∪δ（Ai）。

反之，∪δ（Ai）⊂δ∪（Ai）是显然的。 所以，δ∪（Ai）=∪δ（Ai）。

下面证明（ε，δ）为一对附益算子。设δ（A）⊂B，对a∈A，证明a∈ε（B），因Bc⊂cδ（A），即∀y∈Bc，（a，y）∉R，所以a∈ε（B）。

同样可以证明，A≤ε（B）⇒δ（A）≤B。于是δ（A）≤B⇔A≤ε（B），所以ε 为腐蚀。另一方面，P（X）上的膨胀算子δ:P（X）→P（X）也确定了X 上的一个关系：Rδ=∪{（x，y）|y∈δ{x}}，Rδ称为由δ 诱导的关系。

定理2设δ:P（X）→P（X）为膨胀，Rδ为由δ 诱导的关系，则δRδ=δ。

证明对A⊂P（X），y∈δ（A），存在x∈A 使得（x，y）∈Rδ，于是y∈δRδ（A）。 另一方面，对y∈δRδ（A），存在x∈A 满足（x，y）∈Rδ，可得y∈δ（A）。 所以δRδ=δ。

该节余下部分将讨论关系R 的性质和诱导的形态学算子性质之间的联系。

定义3（1）如果对任意的x∈X，（x，y）∈R，称关系R 是自反的；

（2）如果（x，y）∈R 当且仅当（y，x）∈R，称R 是对称的；

（3）对X 上的两个关系R1，R2，定义

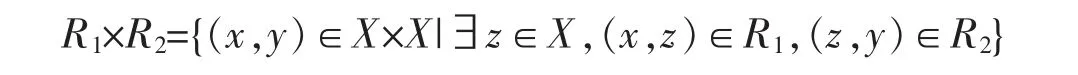
（4）称关系R 是单的，如果（a，x），（b，x）∈R 则a=b；称R 是满的，如果任意y∈X，存在x∈X 使得(x，y)∈R，即δR（X）=X。

定义4（1）对A⊂X，若A⊂δ（A），称δ 是扩张的；

（2）若对任意A⊂B，δ（A）⊂δ（B），则称δ 是单调递增的。

有以下的结论：

定理3设R 是X 上的关系，δ 为R 诱导的膨胀，则：

（1）R 是自反的当且仅当δ 是扩张的；

（2）R1⊂R2当且仅当δ1≤δ2；

（3）X 上的关系R 是单的当且仅当对任意的a≠b，δ（a）∩δ（b）=Ø；

（4）由δ=δ2δ1诱导的关系为R=R1×R2。

证明（1）假设R 为自反的，对任意的y∈A，（y，y）∈R，因为δ（A）={y∈Y|（x，y）∈R，∃x∈A}，所以y∈δ（A），即δ 是扩张的。 反之，如果δ 是扩张的，对任意x∈A，x∈δ（x），由于Rδ=∪{（x，y）|y∈δ{x}}，于是有（x，x）∈Rδ，即Rδ是自反的。

（2）假设R1⊂R2，δ1≤δ2是显然的。 另一方面，若δ1≤δ2，则

（3）设关系R 是单的，若δ（a）∩δ（b）=Ø，任取x∈δ（a）∩δ（b），则有（a，x），（b，x）∈R，所以a=b。 反之，对（a，x），（b，x）∈R，则有x∈δ（a）∩δ（b），于是a=b，即R 为单的。

（4）下面证明R1×R2诱导的膨胀δ 等于δ2δ1。 取

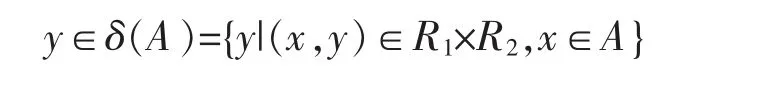
则存在z∈X，使得

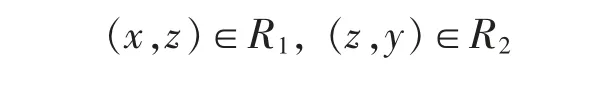
于是z∈δ1，且y∈δ2δ1，即y≤δ2δ1。

反之，对y∈δ2δ1（A），∃z∈δ1（A）使得（z，y）∈R2，故∃x∈A，满足（x，z）∈R1，所以（x，y）∈R1×R2，即y∈δ（A）。

推论1设R1，R2为X 上的关系，δ1，δ2分别是R1，R2诱导的膨胀算子，则

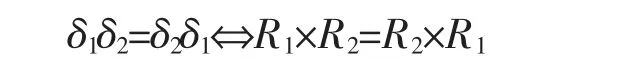
证明显然。

对于交换群G，G 上的关系R 称为是平移不变的，如果对任意的a∈G，（x，y）∈R⇒（x+a，y+a）∈R，称膨胀δ 与平移可交换，如果δ（A+x）=δ（A）+x。

定理4设X 为非空的交换群，R 为X 上的关系，δ 为R 诱导的膨胀算子，则R 为平移不变的当且仅当δ 与平移可交换。

证明设R 平移不变，下面证明δ（A+z）=δ（A）+z。 令y∈δ（A+z），则存在x=a+z∈A+z 使得（a+z，y）∈R，因为R 平移不变，所以（a，y-z）∈R，即y-z∈δ（A），所以y∈δ（A）+z。

类似可以证明δ（A）+z⊂δ（A+z），所以δ（A+z）=δ（A）+z。

反之，假设对任意的A∈P（X），z∈X，成立δ（A+z）=δ（A）+z，取（x，y）∈R，则y∈δ（x），于是

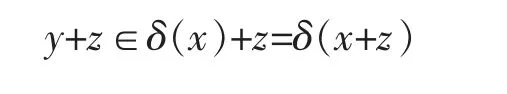
所以（y+z，x+z）∈R。

众所周知对膨胀算子δ:P（X）→P（X），存在唯一的腐蚀ε 与δ 附益，且cεc 也是一个膨胀算子，记为δˇ，其中c 为集合的补运算，但是一般情况δ 不等于δˇ。 类似的cεc 为腐蚀算子，记为ε^，与腐蚀ε^附益的膨胀记为δ^。容易验证δˇ=δ^，为了方便起见，记δT:=δˇ=δ^。对偶地，对腐蚀算子ε:P（X）→P（X），可以定义εT，首先，有以下的定义：

定义5给定非空集合X，若δ=δT，则称δ:P（X）→P（X）是对称的；若ε=εT，则称ε:P（X）→P（X）是对称的。

注2若δ 与ε 是一对附益算子，则δ 是对称的当且仅当ε 是对称的。

注3对X 上的关系R，定义RT如下：（x，y）∈RT⇔（y，x）∈R，如果RT=R，则称R 为对称的。 记R＝R∪RT，则容易验证R 是X 上包含R 的最小的对称关系。

定理5设R 是X 上的关系，δ 为R 诱导的膨胀，则δ 是对称的当且仅当R 是对称的。

证明设R 是对称关系，ε 是R 诱导的腐蚀算子，则

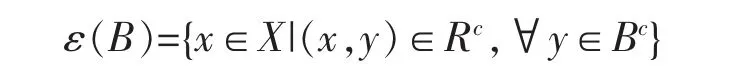
下面证明cεc（A）=δ（A）。

取x∈cεc（A），则有x∉εc（A），由于

故存在y∈A，使得（x，y）∈R，因为R 是对称关系，所以（y，x）∈R，于是x∈δ（A）。反之，对x∈δ（A），则∃a∈A使得（a，x）∈R，所以（x，a）∈R。 因为

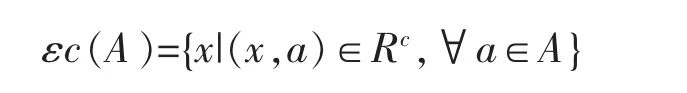
所以x∉εc（A）。

设δ 是对称的，证明R 是对称的。 首先注意到δ 是对称的当且仅当δcδ≤c。 令（x，y）∈R，则成立：

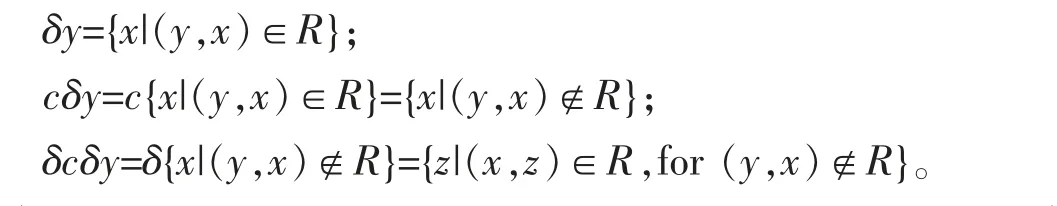
因为δcδ≤c，所以y∉δcδ，即∀（y，x）∉R，（x，y）∉R。 又因为（x，y）∈R，所以（y，x）∈R，即R 是对称的。

2 由关系诱导膨胀的代数性质

该节要给出P（X）上两个膨胀算子的上确界和下确界的概念，并且进一步说明P（X）上所有的膨胀算子构成一个与P（X）同构的完备格。

定义6设δ1，δ2为P（X）上的膨胀算子，定义δ1∨Rδ2如下

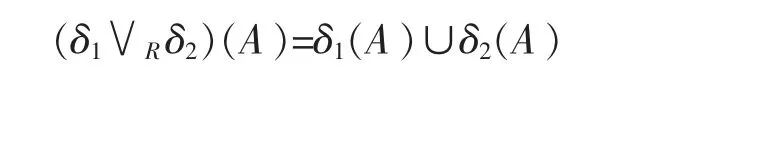
定理6设δ1，δ2分别为R1，R2诱导的膨胀，则δ1∨Rδ2为膨胀，且δ1∨Rδ2=δR1∪R2。

证明对任意A⊂X，证明（δ1∨Rδ2）（A）=δR1∪R2（A）。 假设y∈（δ1∨Rδ2）（A），则存在x∈A 使得（x，y）∈R1或（x，y）∈R2，即y∈δR1∪R2（A）。另一方面，假设y∈δR1∪R2（A），则存在x∈A 使得（x，y）∈R1∪R2，于是（x，y）∈R1或者（x，y）∈R2，所以δR1∪R2（A）⊂（δ1∨Rδ2）（A）。

但是一般情况，若如下定义δ1∧Rδ2:（δ1∧Rδ2）（A）=δ1（A）∩δ2（A），则δ1∧Rδ2不是膨胀算子，但是有以下的结论：

定理7设X 为非空集合，δ1，δ2为P（X）上两个膨胀算子，R1，R2分别是由δ1，δ2诱导的关系，则δR1∩R2是δ1和δ2的最大下界，即δR1∩R2≤δ1，δ2，且对任意δ≤δ1，δ2，均有δ≤δR1∩R2。

证明 因为R1∩R2⊂R1，R1∩R2⊂R2，所以，由定理6 可知，δR1∩R2≤δ1，δ2。 另一方面，对任意的膨胀δ≤δ1，δ2，关系Rδ包含于R1∩R2，于是δ≤δR1∩R2。

于是有以下的定义：

定义7设X 为非空集合，δ1，δ2为P（X）上的膨胀算子，R1，R2分别为δ1，δ2诱导的关系，则定义下确界运算∧R如下：δ1∧Rδ2=δR1∩R2。

则由定理7 可知，∧R为下确界运算，如果R1∩R2=Ø，则由定义可知，对任意A⊂X，（δ1∧Rδ2）A=Ø。

对δ，定义δ 的补为δc=δRc，其中R 为δ 诱导的关系，则有：

定理8设X 为非空集合，δ∈DL（定义见下面），δc为δ 的补，则：

（1）（δc）c=δ；

（2）cδ=δc；

（3）（δ1∨Rδ2）c=（δ1）c∧R（δ2）c；

（4）（δ1∧Rδ2）c=（δ1）c∨R（δ2）c；

（5）δc∨Rδ＝δX×X。证明显然。

定理9设X 为非空集合，则P（X）上所有膨胀算子在运算∨R和∧R下构成一个完备格，记为DL，而且DL 与P（X×X）同构。

证明显然DL 在上确界和下确界运算下成为一个格，为了证明DL 与P（X×X）同构，构造映射为ψ:DL→P（X×X），ψ:δ→Rδ，其中Rδ为δ 诱导的关系，则根据定理2，ψ 是一一映射，且由定理3，ψ 是保序的，再由定理7，ψ（δ1∧Rδ2）＝ψ（δR1∩R2）=R1∩R2，最后根据定理6，ψ（δ1∨Rδ2）＝ψ（δR1∪R2）=R1∪R2。 所以ψ 是从DL 到P（X×X）的同构。