由双分数布朗运动驱动的线性自排斥扩散的最小二乘估计
2020-09-22綦乐天闫理坦
綦乐天, 葛 勇, 闫理坦
(东华大学 理学院,上海201620)
1992年,R.Durrett 等人在文献[1]中对一类刻画增长聚合物形状变化的模型进行了研究。 在一些特定条件下,他们研究了随机微分方程

其中W 是一个d-维标准布朗运动,f 是Lipschitz 连续的。 方程(1)的解Xt是文献[3]中提出并研究的一个离散过程的连续版本。 1995年,M.Cranston 等人在文献[2]中扩展了该模型并建立了自吸引扩散的概念,作为特殊情况,他们研究了线性自交互(即f 是线性的)与常自交互(即f(x)=σ·sign(x),σ>0)两种情形。
若对任意的x∈Rd,函数f 满足x·f(x)≥0,称方程(1)的解为自排斥的;若对任意的x∈Rd,函数f 满足x·f(x)≤0,称方程(1)的解为自吸引的。
值得注意的是这种模型可比拟为一个Ornstein-Uhlenbeck 过程,因此,研究这类方程的渐近行为与参数估计或许是很有意义的。 关于自排斥与自吸引扩散的进一步研究可参阅文献[4-5];关于一般自交互扩散的研究可参阅文献[6-7]。 最近,L.Yan 等人在文献[8]中考虑了随机微分方程
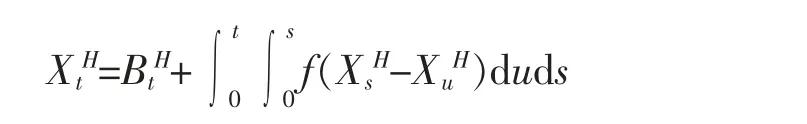
其中BH是一个Hurst 指数为1/2<H<1 的标准分数布朗运动,并作为特例研究了如下线性方程
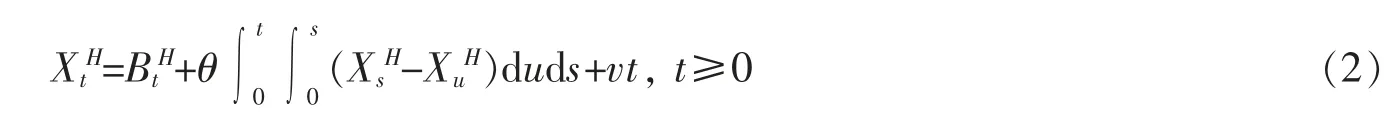
其中θ<0。 并在θ<0,1/2≤H<1 时给出了这个过程的显式解,且证明了当t 趋于无穷时,这个解是均方与几乎必然收敛的。 高辉等人在文献[9]中研究了线性分数自吸引扩散模型的离散刻画,给出了一个逼近并建立了收敛性定理。
另一方面,Y.Hu 等人在文献[10]中研究了由分数布朗运动驱动的Ornstein-Uhlenbeck 过程的参数估计问题,构造了最小二乘估计量并证明了估计量的几乎必然收敛性,并且在Hurst 参数1/2≤H<3/4 时给出了估计量的收敛速度。
受到上述相关研究的启发,文中考虑由双分数布朗运动BH,K驱动如下线性方程的参数估计问题
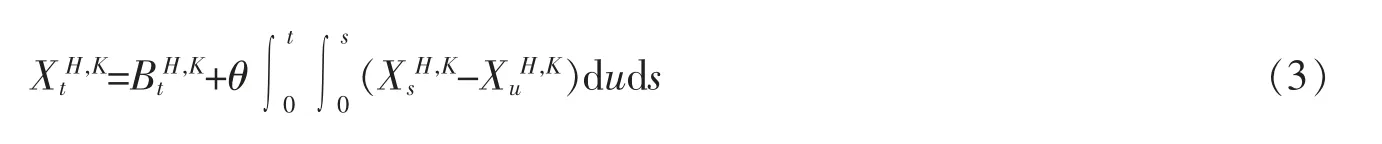
文中内容组织如下:第1 节中,简单介绍双分数布朗运动以及Malliavin 导数等一些基本知识。 第2 节中,给出参数θ 的最小二乘估计量,及文中的主要定理,即的渐进分布。 并为定理的证明建立一些引理。 第3节中,使用第2 节中建立的引理,给出渐进分布的证明。
1 预备知识
众所周知,参数为H,K 的双分数布朗运动BH,K={BtH,K, t≥0}是一个均值为零的,HK-自相似高斯过程,其协方差函数R(s,t)为
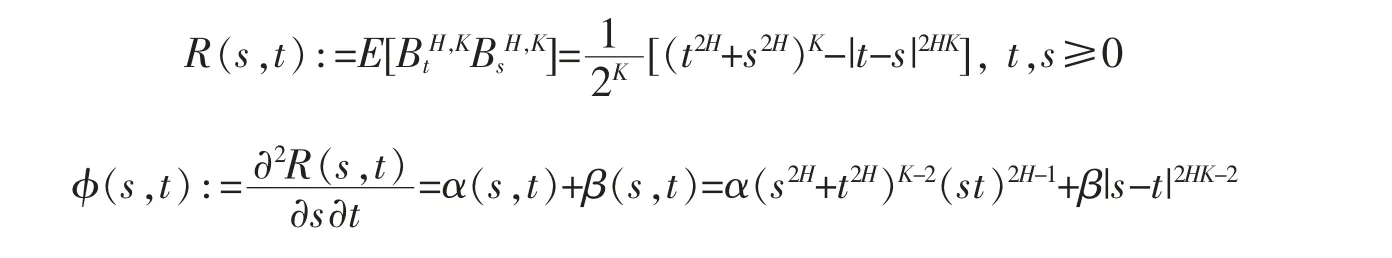
其中α=22-KH2K(K-1);β=21-KHK(2HK-1),且可以证明φ(s,t)是非负的。
H 是一个Hilbert 空间并且当1/2<HK<1 时,有
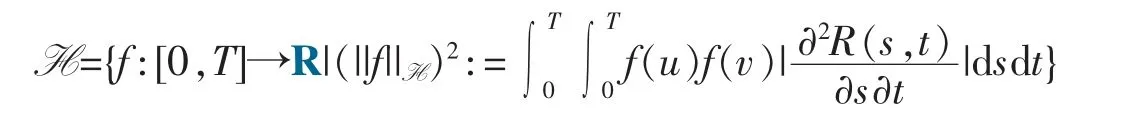
假设用ε 表示由示性函数1[0,t],t≥0 所张成的线性空间。在t≥0 时考虑映射这个映射在ε 上是线性的,并且它是一个从ε 到B 生成的高斯空间的一个等距,这个等距可以被扩张到H 上。称这个等距映射为关于BH,K的Wiener 积分,记成
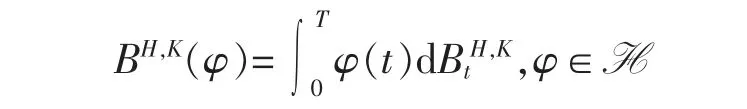
假设δ 表示如下光滑泛函的集合
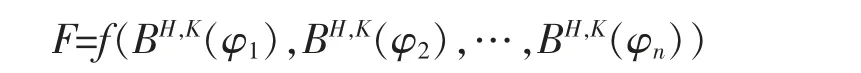
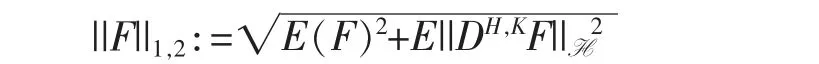
对于如上的F,定义导数算子DH,K(Malliavin 导数)为
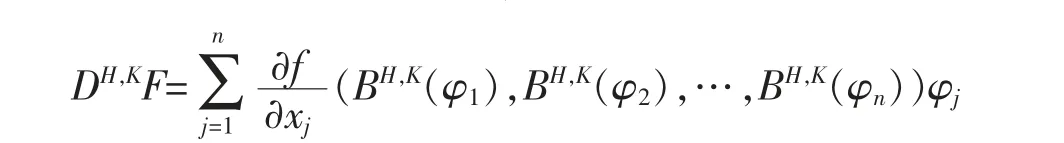
散度算子δH,K是DH,K的对偶,有D1,2⊂Dom(δH,K)并且对任意的u∈D1,2
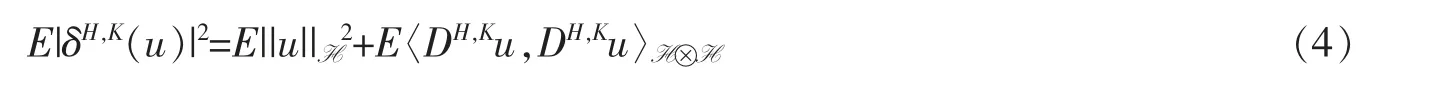
假设1/2<HK<1,如果u 是一个Hölder 连续性指数为α 的过程,且满足α+HK-ε>1(这里的ε 是一个充分小的正数),则Young 积分是适定的。
进一步地,如果u∈D1,2(|H|),有
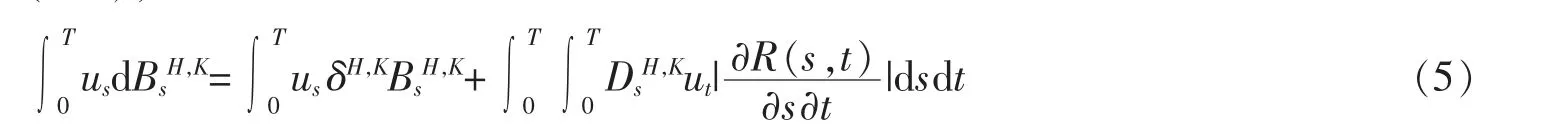
笔者将在接下来的运算中使用到两种积分的转换关系,若采用其他种类的积分,则分析过程则会不同。
2 主要结果及引理
假设C 是一个可能依赖于H,K,θ 的正常数,并且它的值在不同情况下可不同,这种假设同样适用于c。


参照文献[8]可以算出(3)式的解
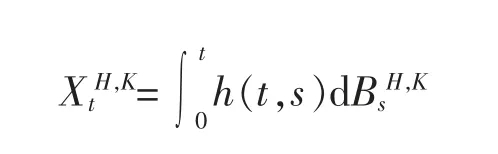
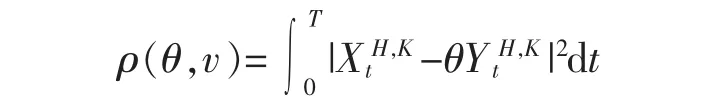
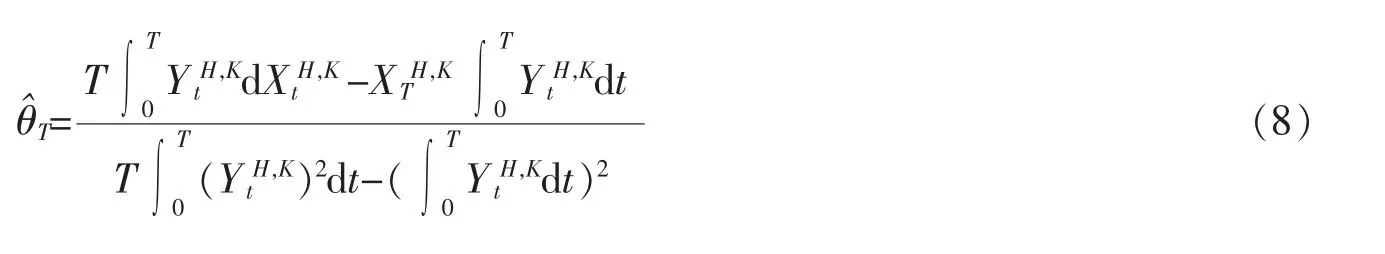
文中主要结果即以下定理:
定理1假设1/2≤HK<1 并且θ>0。 当T 趋向于无穷大时,如下收敛性依分布成立
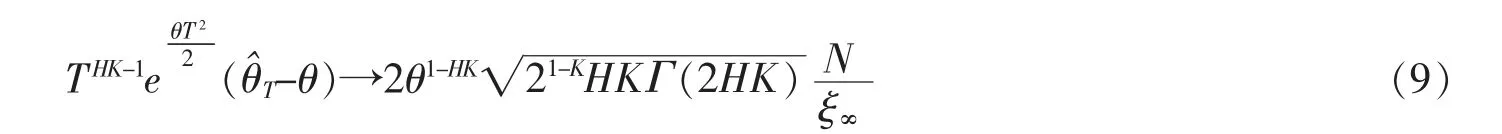
其中N 为一个独立于双分数布朗运动BH,K的标准正态随机变量,并且
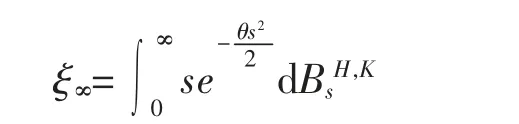
引理1设为所研究方程的解并且θ>0,1/2≤H<1,s,t∈[0,T]。 则
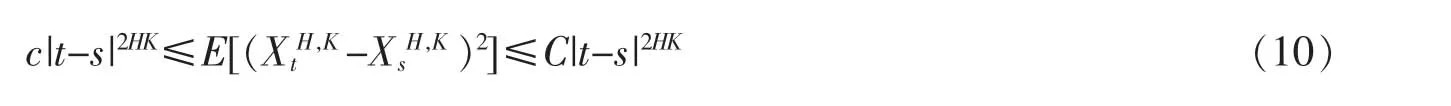
其中C,c 两个常数依赖于T。
证明
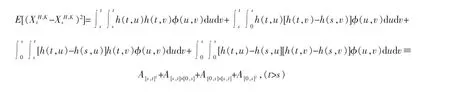
对于A[s,t]2,分别有

由此可知
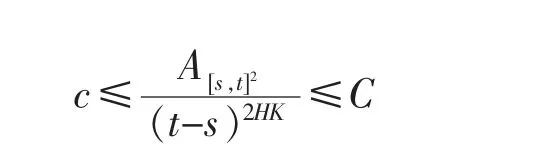
对于A[0,s]2
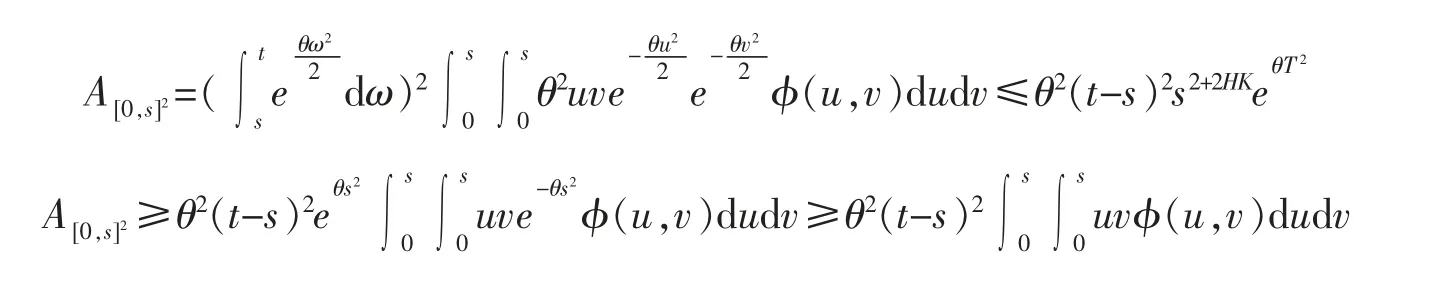
注意到
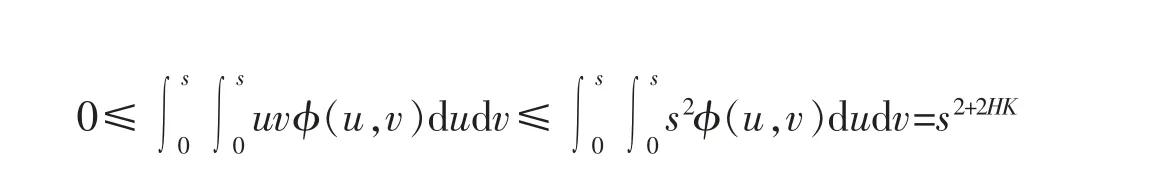
所以一定存在一个适当可以被多项式控制的函数f(s),使得
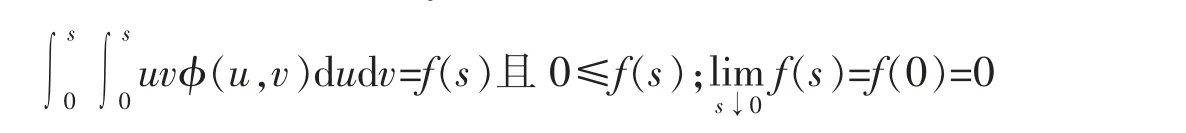
所以可以得到A[0,s]2≥(t-s)2f(s)。 故有
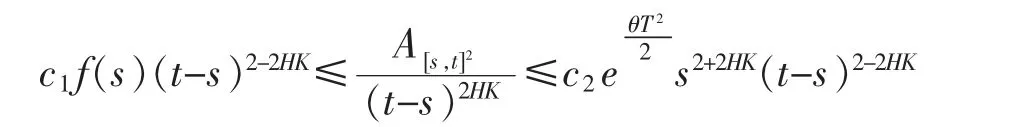
经过相同的分析,A[s,t]×[0,s],A[0,s]×[s,t]都满足同样的性质。 故有
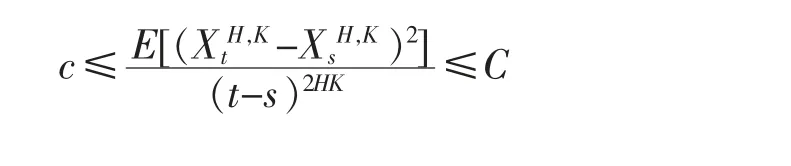
证毕。
由于f(x)足够光滑,所以XtH,K与BtH,K的连续性保持一致,这个结果并不是出乎意料的。
引理2假设1/2≤HK<1。 则随机变量

是一个L2(Ω)空间中的元,并且当T 趋向于无穷大时,ξT以概率1 和L2(Ω)收敛于ξ∞。 进而得知
证明
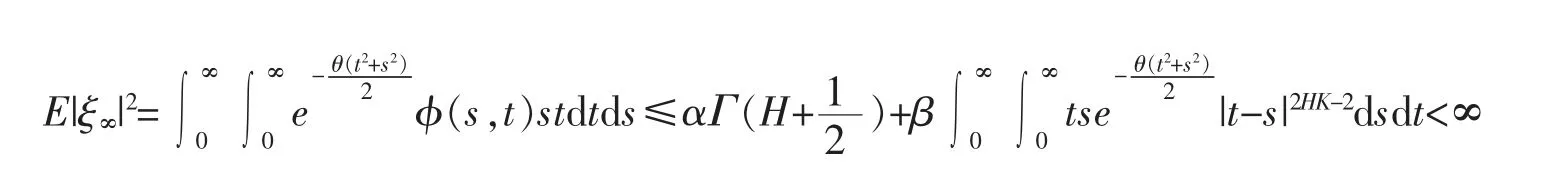
故可以得到:ξ∞是一个L2(Ω)中的元素。
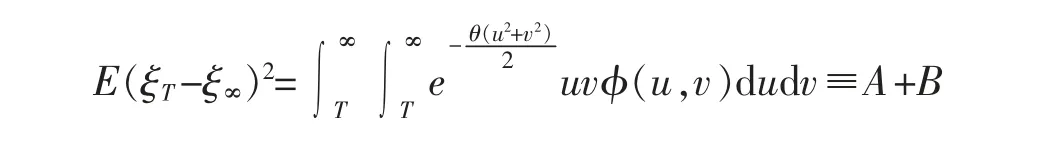
其中
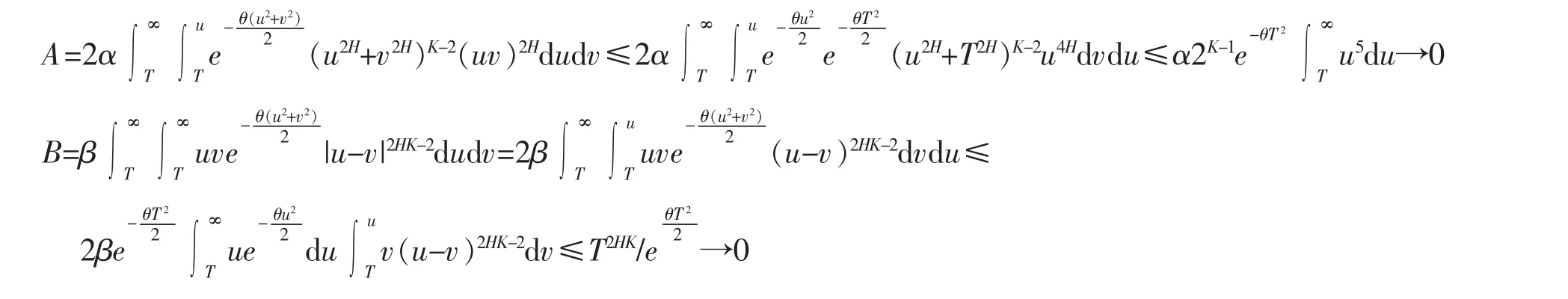
即证明了ξT均方收敛于ξ∞。
再者由分部积分知
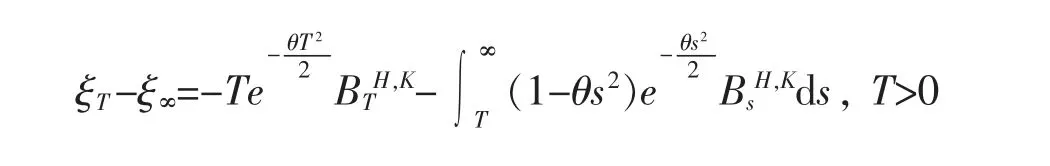
且由事实

与
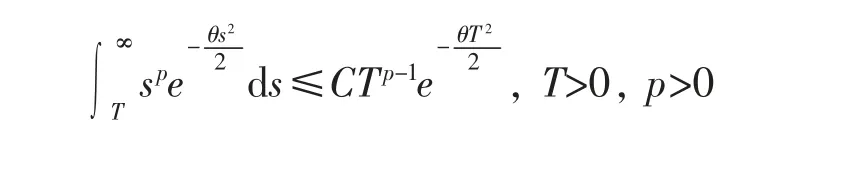
获得估计
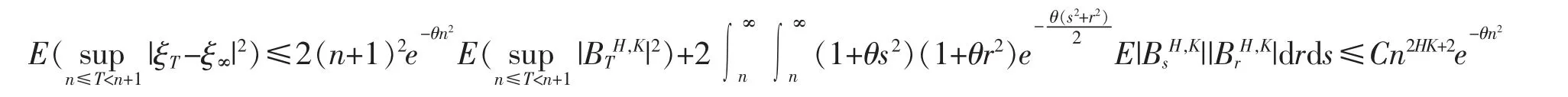
由Borel-Cantelli 引理得:当T 趋于无穷时,ξT以概率1 收敛于ξ∞。
引理3假设1/2≤HK<1。 对任意的有限整数p≥1,当T 趋于无穷大时,几乎必然有
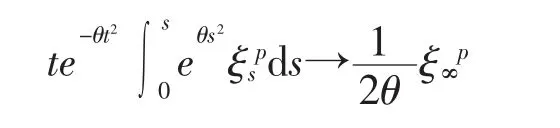
证明
由引理2 以及ξt的连续性,可知:因此,使用洛必达法则可以得到想要的结论。
引理4令1/2<H<1。 当T 趋于无穷时,有
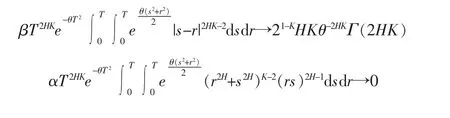
证明

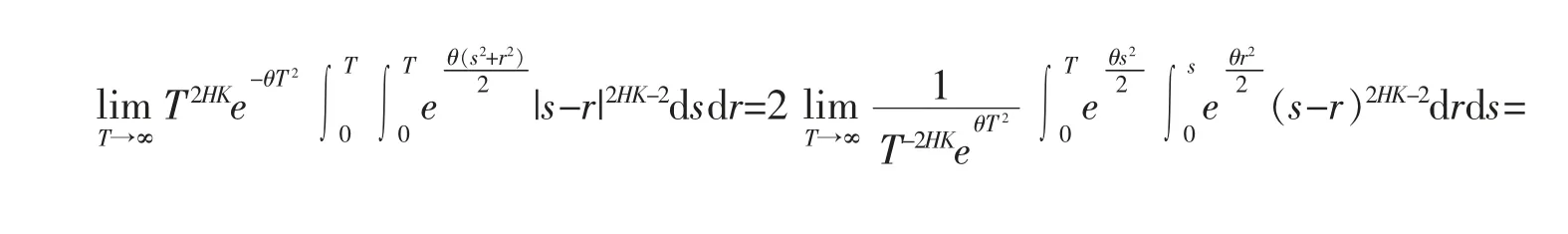
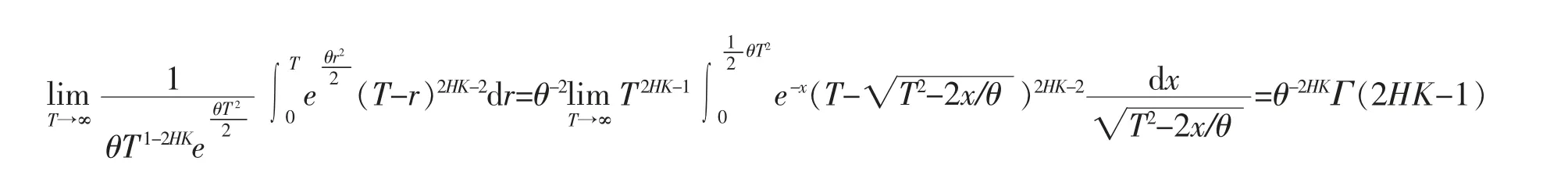
由同样的分析可以得到第二个收敛性。证毕。
引理5假设1/2≤HK<1。则对任意的σ{BtH,K, t≥0}-可测的并满足P(F<∞)=1 的随机变量F,当T 趋于无穷大时,有
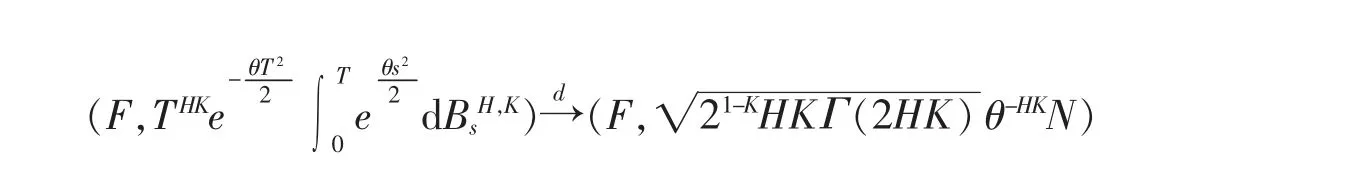
其中N 是独立于BtH,K的标准正态随机变量。
证明
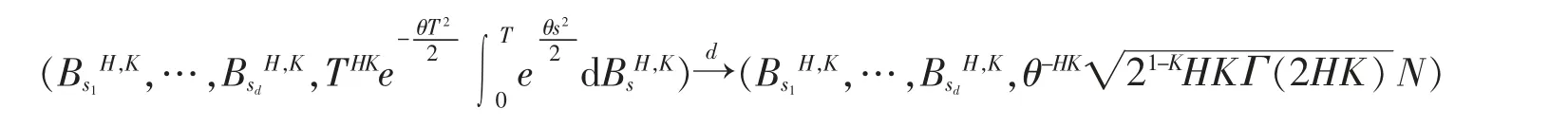
仅需要证明其协方差矩阵的任一元素收敛到0 即可。 对任意固定的s>0,
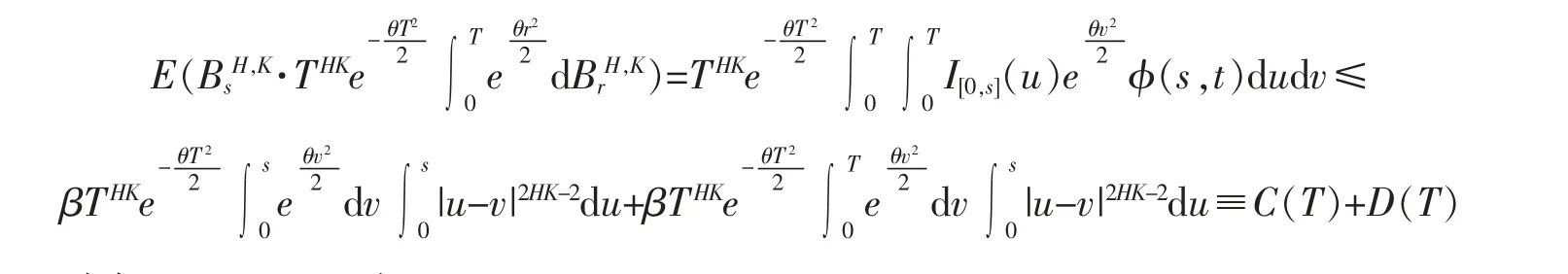
显然,当T→∞时有C(T)→0。 对于D(T)
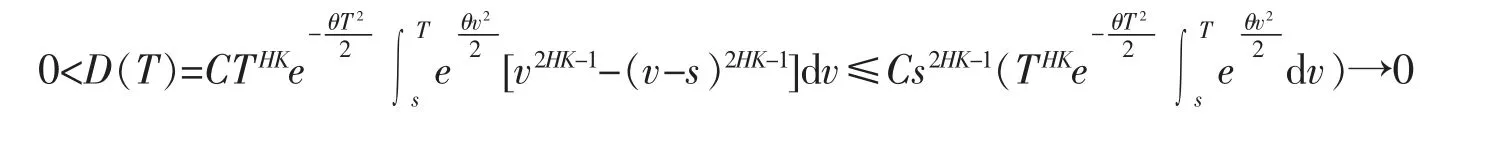
证毕。
引理6对于所有的1/2<HK<1,当T 趋向于无穷大时,如下收敛在L2(Ω)意义下成立
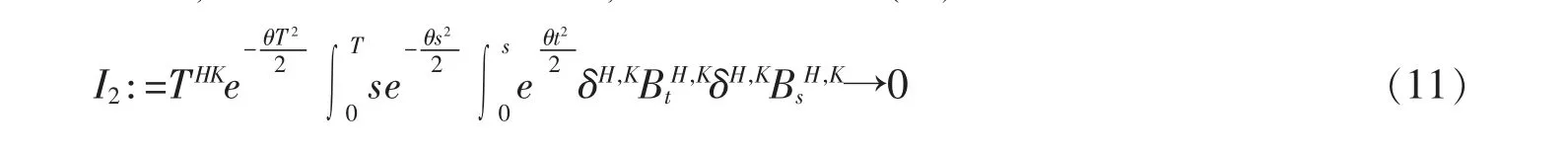
和
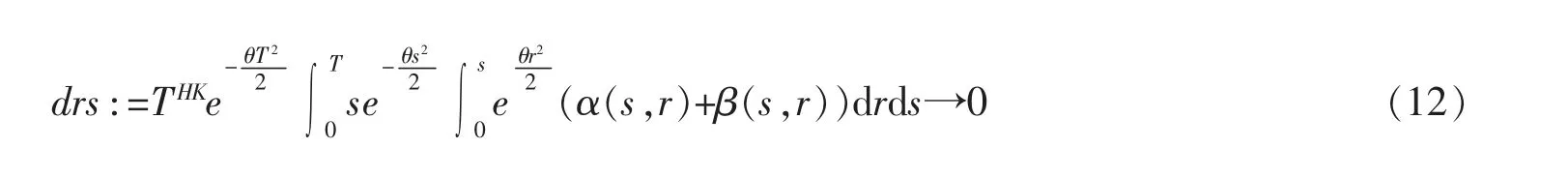
证明
由等式(4),对任意的T>0,获得
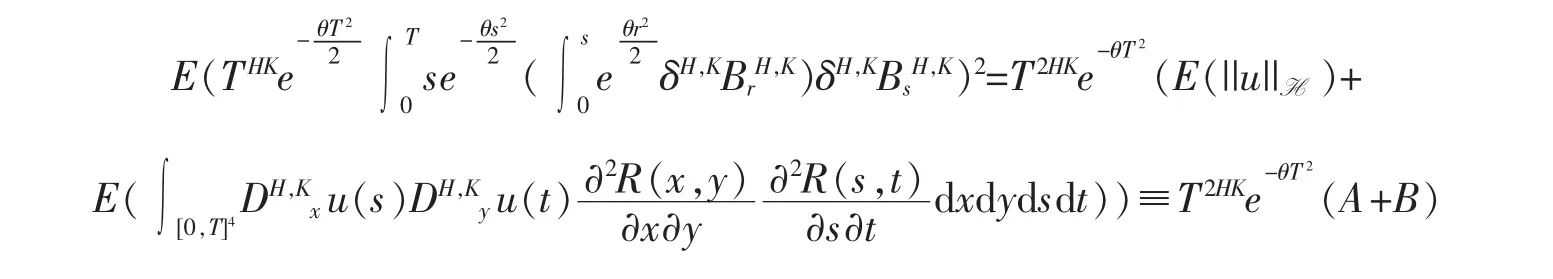
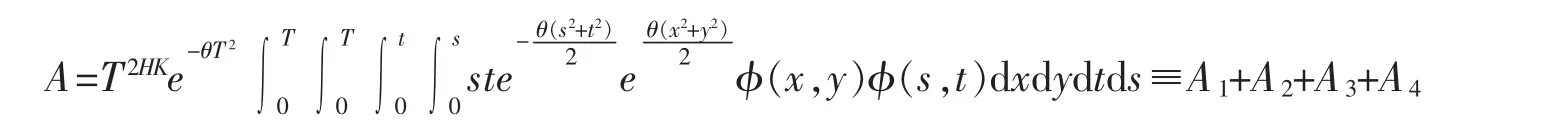
即,将上式拆分成为4 项,分别计算之
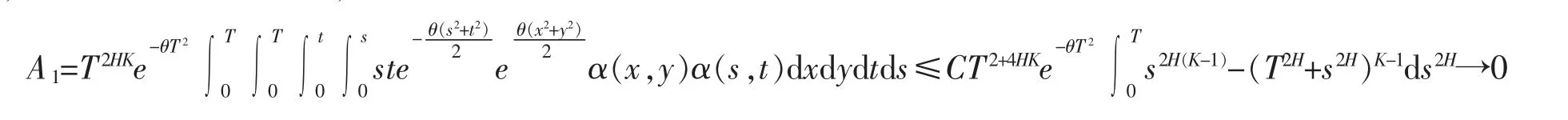
A2在区间s>t,s<t 上的值是一样的,故不妨假设s>t。
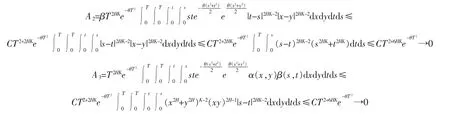
A4的收敛性分析与A3一致,且结论(12)由同样的分析即可得出。证毕。
3 定理1 的证明
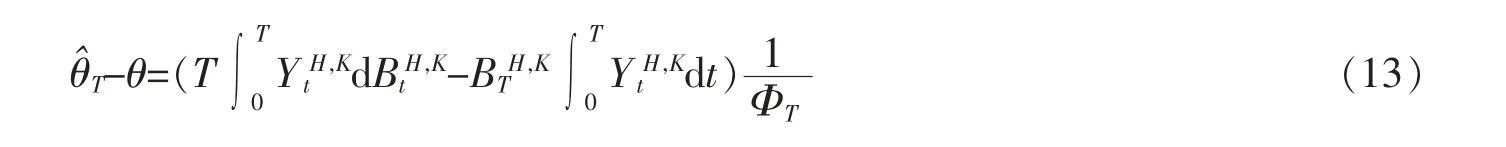
假设1/2<HK<1。 由(7)式、引理3 以及洛必达法则,有收敛性

假设1/2<HK<1。 对任意的T>0,在下式中等号左边代入(13)式后得到
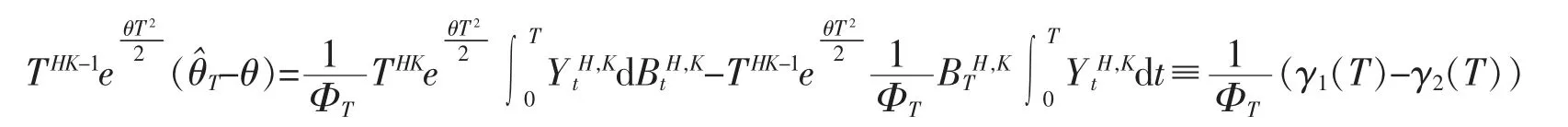
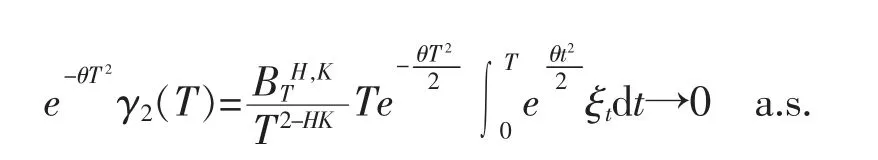
首先,对任意的T≥0,由(5)式以及引理6 得

其次,由(5)式知,对任意的T≥0,有
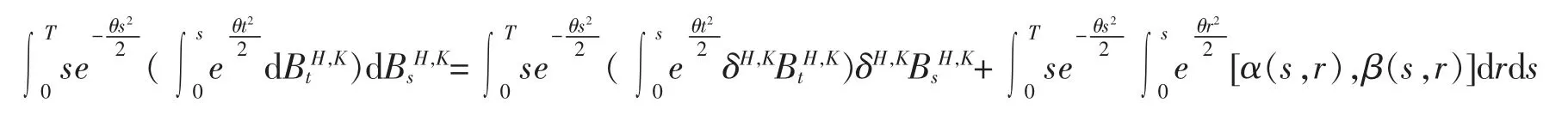
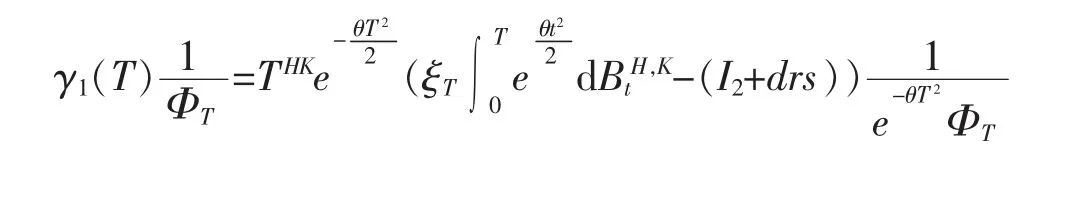
再将(7)式代入下式等号左边,获得最终结合引理5 以及Slutsky 定理,得到
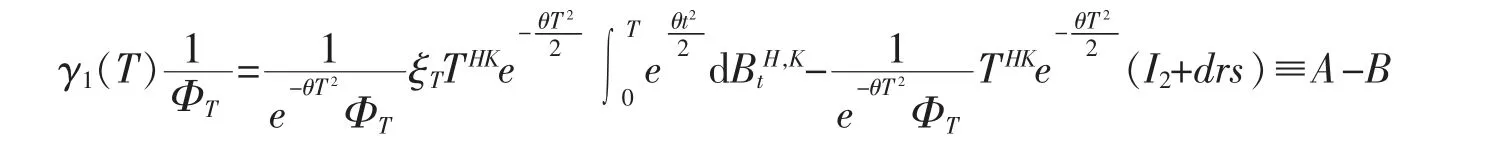
其中
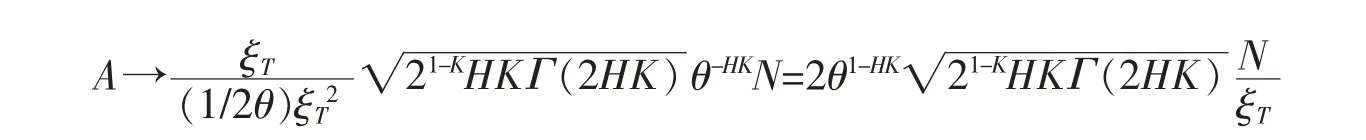
证毕。
