不同荷载条件下低孔隙率砂岩巴西劈裂试验的声发射特性

吴顺川，孙 伟，成子桥

1) 北京科技大学金属矿山高效开采与安全教育部重点实验室，北京 100083 2) 昆明理工大学国土资源工程学院，昆明 650093 3) 中电建路桥集团有限公司，北京 100044

利用巴西圆盘劈裂试验间接测定脆性材料抗拉强度自提出以来，得益于试样制备简单，采用常规压缩试验加载装置，已被广泛地应用[1−2]. 即使在今天，在提出测试方法后的七十多年里，巴西劈裂试验还没有统一明确的标准方法. ASTM[3]建议采用平面与圆盘接触，ISRM[4]建议采用非线荷载弧形夹与试样接触，中国的国家标准和行业标准[5−6]采用与加载板间放有直径为1 mm钢丝为垫条的线荷载与试样接触. 这三种不同的建议方法可以归为两大类：ISRM、ASTM建议方法属于非线荷载（抛物线荷载、正弦荷载等），中国的国家标准和行业标准建议方法属于线荷载. 显然后两者加载装置与试样的接触荷载方式存在很大不同.尽管采用了不同的试验装置，但建议的抗拉强度计算公式却是一致的. Fairhurst[7]首次提出荷载条件对试验结果有影响，在Hondros解的假定下采用Griffith准则分析加载板边缘对解析解的影响，发现增加接触角度，起裂位置会偏离圆盘中心，并提出一个最优接触角度为2arctan(1/8). Erarslan和Williams[8]的研究表明加载装置与试样的接触方式影响峰值荷载、起裂位置、应力分布及I型断裂韧度. 一些学者[9−10]报道了在试验中观察到巴西劈裂试验试样起裂位置经常偏离中心，得出裂纹起裂和扩展的应力区域不同于连续、均质、各向同性材料的结论. Markides和Kourkoulis[11]研究了不同的加载方式，包括线荷载、均布荷载、抛物线荷载及正弦荷载下的巴西破裂数值模型，指出上述不同荷载条件对圆盘主要区域应力分布并不敏感，但在荷载与圆盘接触附近存在差异. Garcia-Fernandez等[12]的研究指出加载板与圆盘接触角度扮演着重要角色，不同的接触角度对应着不同的荷载直径方向上的起裂位置，并得出为确保中心起裂应该增大接触角度的结论. 通过上述研究可以发现，巴西劈裂试验结果容易受到试样的不均质性、加载速率、加载方式、试样尺寸等多种因素的影响，导致圆盘应力分布和起裂位置与理论设想存在较大差别.

1989年以来，声发射监测技术被用于速度场演化、震源位置反演、震源机制等方面，证明了其具有可行性[13−18]. Falls[18]和 Zhang 等[19]采用分布在圆盘前后表面或圆周的声发射传感器收集连续信号，用于确定巴西劈裂试验试样的声发射事件时空演化及震源机制，用于评估试验的合理性. 任会兰等[20]和Zhang[21]等基于声发射技术及矩张量理论研究了混凝土和页岩宏观抗拉破坏的细观裂纹扩展机制. 目前，采用声发射技术研究巴西劈裂试验破裂机制的研究依然很少. 基于此，本研究采用声发射监测技术研究低孔隙率砂岩在线/非线荷载条件下的圆盘试样损伤三维演化及震源机制，并评估不同荷载条件对巴西劈裂试验抗拉强度的影响，以试图定量描述荷载接触条件对巴西劈裂试验的影响.

1 试验方法

1.1 试样制备

为保证试样的一致性，本研究所用的低孔隙率砂岩来自四川自贡地区，巴西圆盘试样均取自同一岩块，所用试样沿同一方向钻取. 主要由长石、石英、氧化镁和黏土矿物组成，平均颗粒半径约为0.1 mm，孔隙率约为6.5%，有关自贡砂岩的物理性质描述见系列试验[19, 22−23]. 试样尺寸满足 ISRM建议的试验标准，即圆盘直径等于50 mm，厚度为25 mm，直径与平均晶粒尺寸之比大于 10∶1. 此外，选用的试样保证两端面不平整度误差及直径的误差控制在±0.02 mm以内.

1.2 试验装置及过程

图1（a）展示了传感器的三维布置方式，巴西圆盘一个平面上布置4个Nano30声发射传感器，距离圆盘中心15 mm以90°等角分布. 另一面同样布置4个Nano30声发射传感器，以90°等角分布，距离圆盘中心15 mm，与对面传感器错开45°，相当于对面传感器顺时针旋转45°. 试样与传感器接触部位均匀涂抹耦合剂（硅脂），特制的夹具用于确保传感器与试样表面的接触稳定，以提高弹性波的传递及信号的接收. 非线荷载加载夹与试样之间放置减摩片，以减少端部摩擦. 试验前，分别对无应力状态下的线/非线荷载巴西圆盘试样进行2次波速测量，用于检测传感器与试样表面的耦合情况，同时测量传感器安装精度及定位误差的计算. 试验中线/非线荷载以相同的荷载加载速率加载直至试样破坏. GAW-2000型微机控制电液伺服刚性压力试验机的加载速率均为 30 N∙s−1，保证其准静态加载.

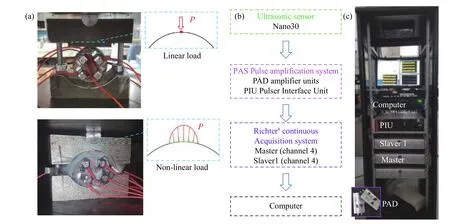
图1 加载装置及声发射信号采集流程. （a）两种加载方式装置；（b）声发射采集系统原理；（c）声发射采集系统实物图Fig.1 Loading devices and acoustic emission signal acquisition setup:(a) two different loading devices; (b) schematic diagram of AE acquisition system;(c) photograph of AE acquisition system

1.3 声发射数据采集

图1（b）和图1（c）展示了声发射信号连续采集的流程及原理. 砂岩试样中的微裂纹破裂及人工震源产生的扰动被试样表面的Nano30传感器监测后，以电压的形式传输给 100 kHz～1 MHz 带通的PAD放大器单元. 信号被前置放大，增益值设定为30 dB. 而后信号传输到Richter8连续采集系统，进行信号连续采集，采集的数据被存储到固态硬盘中. Richter8系统由Master-Slaver1组成，每个Richter可同步连续采集4个通道的数据. 为测试传感器安装及定位精度，在加载前，由脉冲发生器接口单元PIU依次从传感器S1到S8发射500 V脉冲. 500 V脉冲作为人工震源，剩余的7个传感器作为接收器记录信号.

2 试验分析及结论

2.1 传感器阵列及定位精度分析

试验前对试样进行了2次无应力状态波速测量，以测量2为例，500 V高压脉冲从S2发射，S1、S3～S8作为接收器接收信号，通过P波自动到时拾取而获取到时时差，而后采用网格坍塌搜索算法进行定位. 网格坍塌搜索算法是一种常用的定位算法，Geiger法仅适用于各向同性介质易产生极大定位误差，而单纯形法迭代搜索最小残差使其无法获取全局最优解. 网格坍塌搜索算法适用于非均质性和各向异性速度模型，可获得全局最优解及产生较小的定位误差[23]. 将两组脉冲事件（人工震源）定位结果与已知传感器位置进行对比，非线荷载条件下的定位结果如图2（a）所示. 两种加载板条件下的结果表明定位误差在北、东上的分量的绝对值均不超过 9 mm. 图 2（b）给出了阵列分析工具和 L2 范数计算对假象坐标点 (N,E,D) = (10 mm,0, 0)的定位残差，定位残差为0-3.08E-6之间，表明传感器排布有很好的监测效率. 综合以上，可认为本研究传感器布设方式的定位精度较高，是合理可靠的.

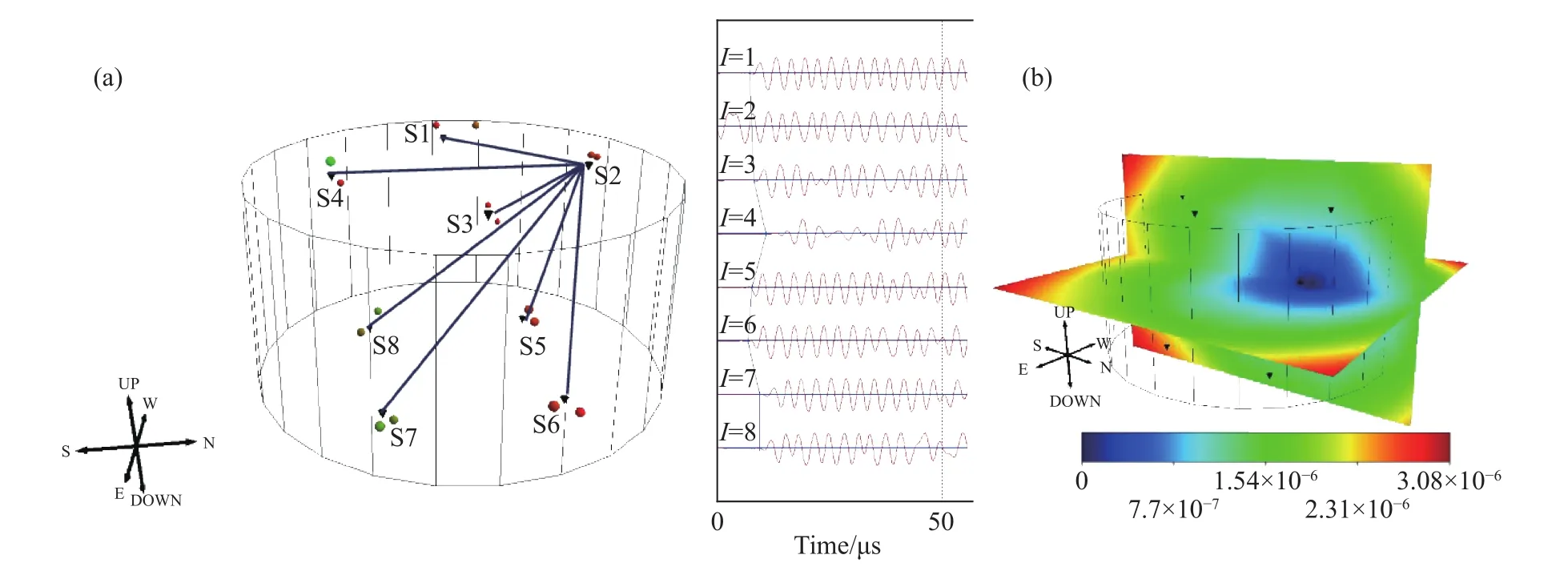
图2 传感器三维定位残差及主动震源定位结果. （a）主动震源定位结果及传感器2波形信号；（b）定位残差密度切片Fig.2 Misfit space density plane of 3D sensor array and active source locating result:(a) active source location result and the waveforms obtained through Survey 2; (b) density planes of misfit error

2.2 声发射特征分析对比

图3（a）展示了线荷载条件下巴西圆盘劈裂试验声发射特性，试验过程一共采集了354 s连续声发射波形信号. 采用触发比率为0.5的拾取算法将连续声发射信号进行触发处理，满足不少于4个通道的波形存储记录204.8 μs的数据. 一共1131个有效定位声发射事件，其有效定位事件破裂震级三维分布及时空演化如图4所示. 根据有效定位事件频率的变化将线荷载试验过程划分为4个阶段：阶段1，有效定位事件有20个，频率最低（不超过 1 s−1），破裂震级不超过−4.21. 阶段 2 持续时间从 202.1992249 s至 304.9882426 s，一共有 412 个有效定位事件，随时间不断增加，阶段末出现有效声发射事件集中剧烈增加现象，最大频率为48 s−1，破裂震级最大为−3.38. 圆盘起裂位于圆盘中心上、下约15 mm，且圆盘中心以上起裂面积大于圆盘以下. 阶段3持续时间从306.1193752 s至334.8700203 s，一共有 265个有效声发射定位事件，有效声发射定位事件频率随时间分布较为均匀且相对较低（1～7 s−1），在阶段末最大有效声发射事件频率剧增至 47 s−1，破裂震级最大为−2.78，位置基本与阶段1相同，且圆盘中心以上更为集中.阶段 4 持续时间从 336.0350351 s至 353.9187746 s，有434个有效定位事件，此阶段开始有效定位事件频率相对较低，约为 5 s−1，事件集中剧烈增加发生在阶段末，为 234 s−1，破裂震级最大为−2.84. 位置主要集中在圆盘中心以上12 mm，且偏离中心位置.

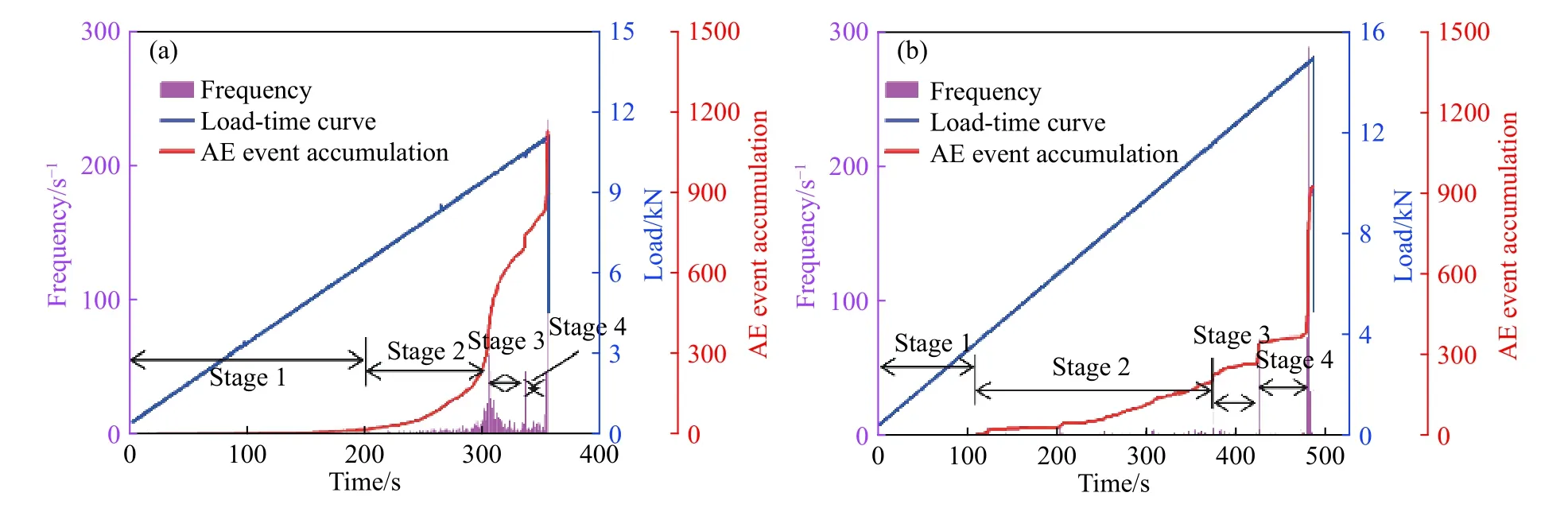
图3 荷载、声发射事件累计数及频率与时间的关系. （a）线荷载；（b）非线荷载Fig.3 Variations of load, AE event accumulation and located AE rate with time:(a) linear load; (b) non-linear load

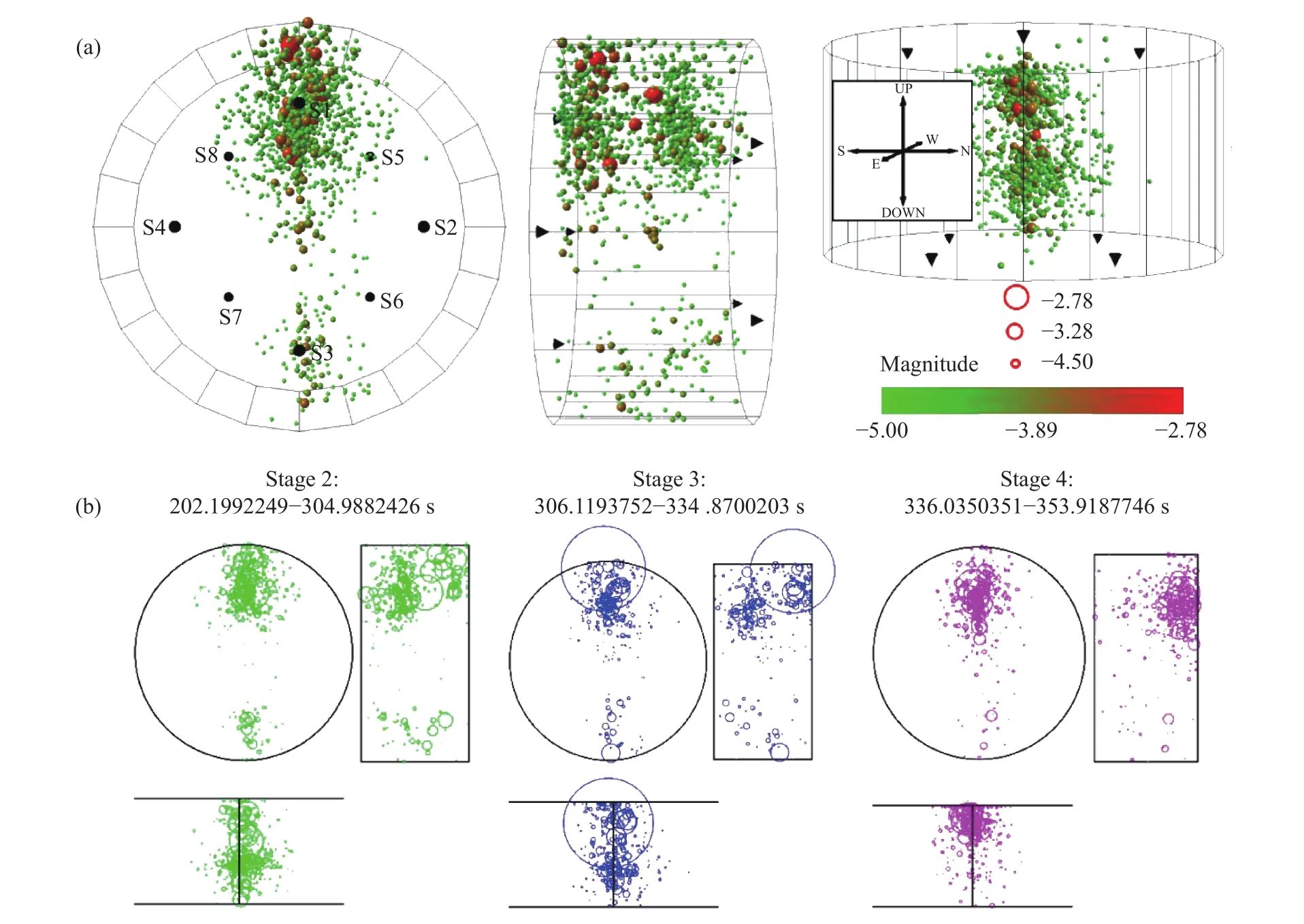
图4 线荷载条件下声发射事件破裂震级及时空演化. （a）破裂震级三维视图；（b）不同阶段有效声发射事件增量（依据信噪比绘制）Fig.4 Located magnitude and spatial evolution of AE events for the linear load:(a) the located magnitude shown in the 3D model; (b) the effective AE increment at different stages (marker sizes are scaled by signal to noise ratio)

图3（b）展示了非线荷载条件下巴西圆盘劈裂试验声发射特性，试验过程中一共采集了484 s连续声发射波形信号. 一共931个有效定位声发射事件，其有效定位事件破裂震级三维分布及时空演化如图5所示. 同样，根据有效定位事件频率的变化将线荷载划分为4个阶段：阶段1，有效定位事件频率最低（1 s−1），破裂震级为−4.41；阶段 2 持续时间从 100.5892033 s至 371.9930491 s，一共有203个效定位事件，随时间不断增加阶段末出现有效声发射事件集中剧烈增加现象，最大频率为21 s−1，破裂震级最大为−3.48. 巴西圆盘起裂位于圆盘中心以下约 12 mm；阶段 3持续时间从 373.4738827 s至423.9923606 s，一共有71个有效声发射定位事件，频率随时间先减小后出现剧烈增加，最大有效声发射事件频率由约 3 s−1剧增至 72 s−1，破裂震级最大为−3.24，位置与阶段1相比稍微靠近圆盘中心；阶段 4 持续时间从 425.0513716 s至 484.2164435 s，一共有654个有效声发射定位事件，开始阶段有效定位事件频率相对较低，约为 2 s−1，事件集中剧烈增加发生在阶段末，频率为 289 s−1，破裂震级最大为−2.09. 整体来说，非线荷载条件下有效声发射事件定位位置较为分散，但基本位于加载方向，与实验结果较为一致.

通过对线/非线荷载条件下巴西劈裂试验试样损伤演化对比，可以得出以下结论：相同加载速率下，阶段2～阶段4的声发射事件发生在不同的位置，均随着荷载的增加，平均震级随之增大. 声发射信号的信噪比亦呈增大趋势，表明裂纹破裂释放的能量随着试样接近破裂越来越大. 线荷载条件下显著减缓了圆盘损伤累计的时间和释放能量的大小，使得微裂纹迅速成核、扩展及贯通，达到破坏峰值强度后发生剧烈的脆性破坏. 非线荷载条件下巴西劈裂试验起裂时刻早于线荷载，且裂纹稳定扩展阶段（阶段2）时间较长，表明非线荷载方式可有效控制微裂纹的稳定扩展. 这种现象可以解释为非线荷载条件下随着接触面积增大，使圆盘受力面积增大，减缓了应力集中，使圆盘内部微裂纹稳定扩展.

采用三点法[24]计算了裂缝网络的几何形状，所得的极分布被投影到下半球，密度高的区域表明存在优先取向. 有效定位声发射事件的极点密度如图6所示，结果表明线/非线荷载巴西圆盘破裂面均在整体上近似垂直. 然而，线荷载条件下巴西圆盘破裂面的走向分布在W12°N至W15°S范围内，非线荷载条件下巴西圆盘破裂面的走向分布在W18°N至W20°S范围内，表明非线荷载破裂面的局部扭曲程度大于线荷载. 作为对比，非线荷载条件下得到的宏观破裂面局部扭曲程度亦大于线荷载.

采用Gutenberg-Richter关系式[25]表示震源与频率的关系：

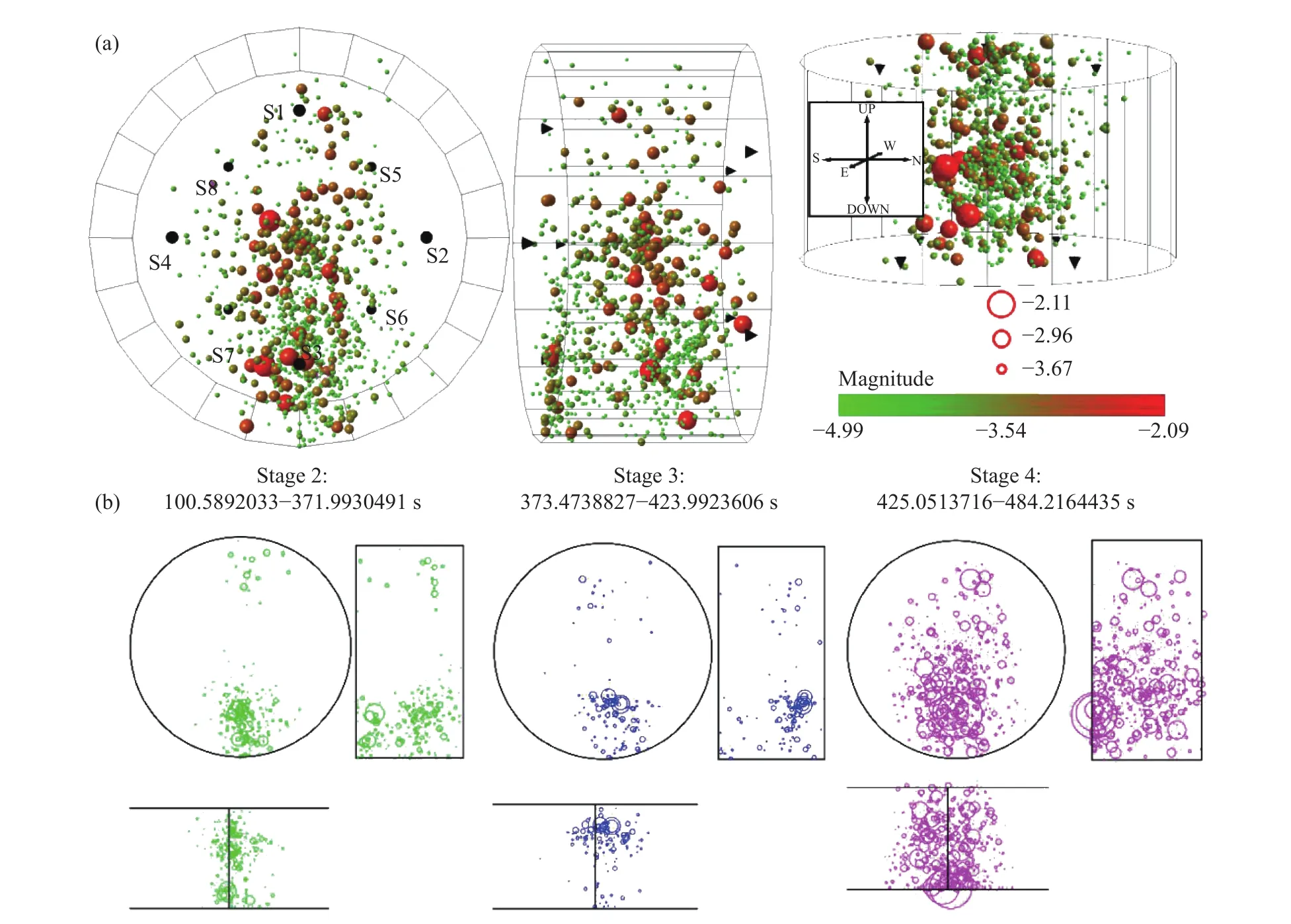
图5 非线荷载条件下声发射事件破裂震级及时空演化. （a）破裂震级三维视图；（b）不同阶段有效声发射事件增量（依据信噪比绘制）Fig.5 Located magnitude and spatial evolution of AE events for the non-linear load:(a) the located magnitude shown in the 3D model; (b) the effective AE increment at different stages (marker sizes are scaled by signal to noise ratio)

图6 微裂纹极点密度及宏观破裂面模式. （a）线荷载；（b）非线荷载Fig.6 Stereonets of microcrack pole density and macroscopic fracture modes:(a) linear load; (b) non-linear load

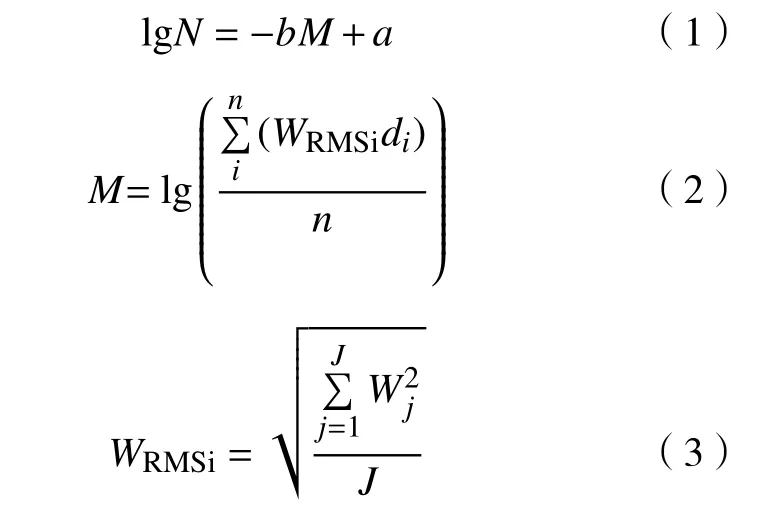
式中，a为常数；b通常称为b值，其变化规律可为前震提供先兆信息，是震级分布及能量释放剧烈程度的重要指标；N为不超过相对震级M的有效定位事件累计数；n为传感器数量；di为第i个传感器和震源之间的距离，m；WRMSi是第i个传感器波形幅度的均方根；Wj是第i个传感器的所有J个采样点的第j个振幅点. 图7展示了线/非线荷载声发射事件累计次数lgN与相对震级M之间的关系. 线荷载条件下声发射有效定位事件震级分布在−5.0～−2.78之间，震级M大于−4.0的声发射事件占8.95%. 震级在−5.0～−4.50声发射事件出现的次数最为集中，有效定位事件累计数呈递减分布，当向右端移动时，有效声发射事件累计数骤然下降，且越来越低. 非线荷载条件下，声发射有效定位事件震级分布在−4.99～−2.09之间，震级M大于−4.0的声发射事件占36.3%. 有效定位事件累计数分布规律与线荷载条件下一致. 线荷载条件下，声发射有效定位事件的累计频数lgN与相对震级拟合直线方程为：

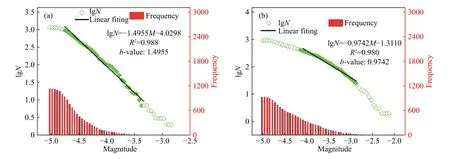
图7 声发射事件频数、累计数与震级 M 的关系. （a）线荷载；（b）非线荷载Fig.7 Relationship between the frequency, cumulative number and magnitude M of AE events:(a) linear load; (b) non-linear load

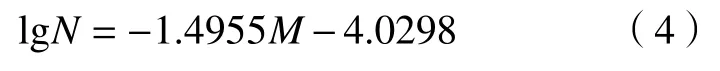
式中，常数a为−4.0298，b值为 1.4955，R2=0.988. 此外，线性荷载条件下另一组砂岩巴西劈裂试验的b值为1.3724[19]，两组试验的结果显示了较好的一致性. 非线荷载条件下，声发射有效定位事件的累计频数lgN与相对震级拟合直线方程为：

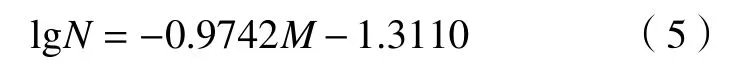
常数a为−1.3110，b值为 0.9742，R2=0.980.

表1给出了线/非线荷载条件下巴西圆盘的声发射特征结果，通过对比可以得出以下结论：相同加载速率下，线荷载较大震级事件较非线荷载少，b值较非线荷载要大. 震级分布结果表明线荷载条件能有效控制大震级声发射事件的产生. 其原因可能是线荷载条件下施加面积较小，在小面积荷载条件下巴西圆盘边缘产生了应力集中，发生了局部剪切破裂而诱发圆盘的整体破裂.

表1 线/非线荷载条件下声发射特征对比Table 1 Comparison of acoustic emission characteristics under linear/non-linear loading

2.3 震源机制反演

采用Knopoff 和Randal[26]提出的矩张量反演方法分析线/非线荷载过程中微裂纹破裂机制，将矩张量分解为各向同性部分（ISO）、纯双力偶（DC）和补偿线性矢量偶极成分（CLVD）. 其中ISO部分可表示理想爆炸源或内缩源，DC成分可代表剪切破裂或者断层的相对错动机制，CLVD成分为补偿体积变化在平行于最大主应力的平面内产生的质点运动[27]，矩张量各分量成分占比采用PISO、PDC和PCLVD表示，公式计算如下：

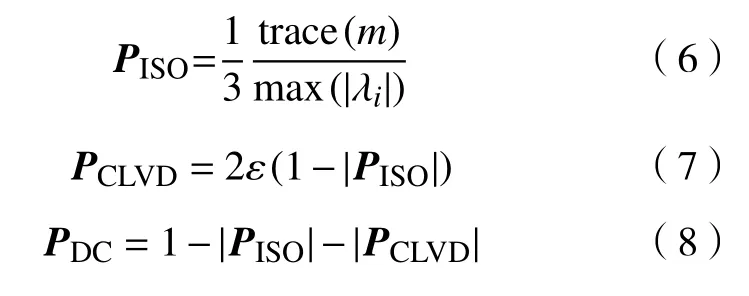
式中，trace(m)为 3×3 矩阵的迹；λi为矩张量的特征值；ε为衡量CLVD成分相对于DC成分大小的参数：

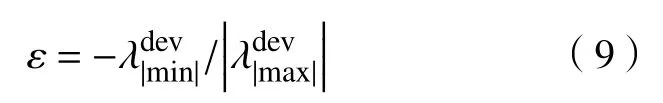
图8（a）给出了线荷载条件下AE事件的矩张量分解的成分比例统计分析结果用以定量分析破裂类型. ISO、DC和CLVD成分比例分别主要分布在−60%～70%、−100%～100%和−100%～100%之间.依据Ohtsu[28]提出的判断破裂类型的方法，张拉破裂、剪切破裂及混合型破裂占比分别为47.76%、24.79%及 27.35%. 图8（b）给出了非线荷载条件下，ISO、DC和CLVD成分分别主要分布在−55%～55%、−100%～100%和−100%～100%之间. 依据Ohtsu的破裂类型的判断方法，张拉破裂、剪切破裂及混合型破裂占比分别为48.92%、23.09%及28.03%.

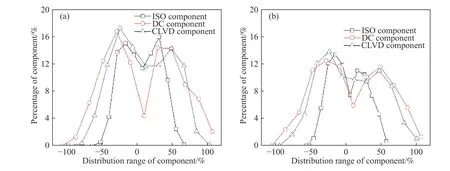
图8 矩张量成分占比. （a）线荷载；（b）非线荷载Fig.8 Percentage of component of moment tensor components for the linear load:(a) linear load; (b) non-linear load

为进一步揭露震源机制，采用沙滩球表示单个震源破裂方位，以便直观地展示三维坐标系下岩石破裂方位（走向、倾角）等震源机制解[29−31]. 从线荷载条件下巴西劈裂试验的有效声发射定位事件选取震级最大的5个事件进行矩张量分解，计算的破裂方位用沙滩球表示，如图9（a）所示. DC成分对于理解试样断裂过程起着重要的作用，DC成分百分比最小为−55.8%，最大为45%. 其中2个的震源机制为剪切破坏（Majority DC），其余3个为非剪切破坏（Majority non-DC）. 非线荷载条件下巴西劈裂试验的最大的5个有效定位事件的分解结果如图9（b）所示. DC成分百分比最小为−87.3%，最大为46.5%. 其中，3个的震源机制为剪切破坏（Majority DC），其余 2个为非剪切破坏（Majority non-DC）.

表2展示了线/非线荷载条件下巴西圆盘的震源机制结果，通过对比分析可以得出如下结论，线/非线荷载条件下巴西劈裂试验微裂纹破裂主要由张拉及剪切两种破裂形式. 值得注意的是，其张拉破裂、剪切破裂所占比例接近，这是前人所没有揭示的. 破裂的机制均可以解释为近似平行于荷载方向上的张拉裂纹的萌生、扩展及贯通.

3 起裂位置及评估抗拉强度的讨论

许多 研 究学 者[8, 11, 32−33]报道 了 岩石 或 类 岩 石材料巴西劈裂试验起裂位置偏离中心的现象，即便对平面加载装置进行了很多改进，如弧形加载夹、垫条加载等，但巴西圆盘起裂位置偏离中心的现象仍然常常发生. 本研究中，线荷载条件下，低孔隙率砂岩圆盘试样的起裂位置位于圆盘中心上方15 mm左右，而非线荷载条件下，起裂位置在圆盘中心下方12 mm左右，两者不同阶段声发射事件发生在不同的位置. 线/非线性条件下，巴西圆盘试样的起裂位置均不在圆盘中心，与二维理论假定存在较大出入. 巴西破裂试验圆盘假定的二维受力条件实际是三维的，并且荷载条件对圆盘起裂位置影响显著，随着荷载接触面积的增大巴西圆盘起裂位置向圆心位置靠近，这与Garcia-Fernandez等[12]的研究结论一致.

线荷载条件下巴西劈裂试验的破裂峰值荷载为 11.10 kN，非线荷载条件下为 15.02 kN. 此外，还分别进行了3组无声发射监测的线荷载条件下的巴西劈裂试验，其峰值荷载的均值为9.96 kN；非线荷载条件下的巴西劈裂试验，其峰值荷载的均值为14.67 kN[19]. 两者的峰值荷载存在差异，非线荷载条件下，巴西劈裂峰值荷载大于线荷载条件，这与Komurlu和Kesimal[34]及Erarslan等[35]的研究结论一致. 本研究中，声发射事件均分布在圆盘非中心位置，也从声发射角度表明两种加载装置的荷载条件并不能保证巴西圆盘中心起裂，荷载接触面积应比ISRM建议的标准巴西破裂试验大，以进一步减弱圆盘与加载装置接触部位的应力集中现象，这与前人[8, 36]的试验观察和数值分析结果一致.因此，由于巴西圆盘非中心起裂，可以推测其峰值荷载计算得到的抗拉强度可能要比真实值低.

4 结论

本文采用声发射监测系统，监测低孔隙率砂岩巴西圆盘在线/非线荷载条件下破坏过程中的声发射事件数量、能量特征、破裂机制等，从声波信号上探索相同加载速率下不同荷载条件试样三维损伤演化及震源机制的异同点，具体结论如下：

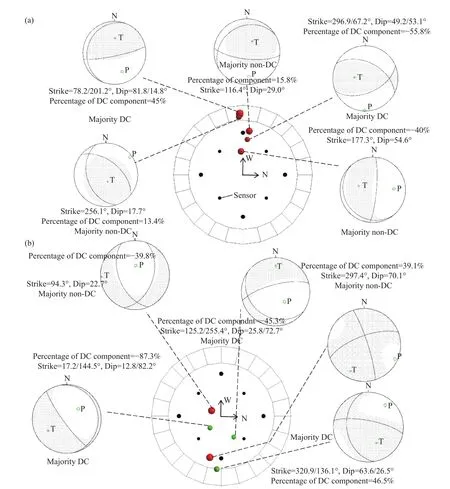
图9 震级最大的 5 个声发射事件震源机制解. （a）线荷载；（b）非线荷载Fig.9 Focal mechanism solutions of the five AE events with the largest magnitude:(a) linear load; (b) non-linear load

表2 线/非线荷载条件下震源机制对比Table 2 Comparison of focal mechanisms under linear/non-linear loads

（1）线/非线荷载条件下，低孔隙率砂岩圆盘试样在相同加载速率下均为非中心起裂，两者不同阶段声发射事件发生在不同的位置. 随着试样荷载的增加，信噪比和平均震级均随之增大，裂纹破裂释放的能量随之增大. 特别是峰值附近，声发射事件异常活跃，声发射累计数及频率呈跳跃式增长.

（2）圆盘所受荷载面积显著影响损伤累计的时间和释放能量的大小. 非线荷载较线荷载条件，其圆盘所受荷载面积逐渐增大，增加了损伤累计的时间和声发射事件的剧烈程度，有效地控制了裂纹的稳定扩展，使得最终贯通发生的脆性破裂更剧烈. 圆盘接触面积的变化，减弱了荷载接触附近区域的应力集中现象，从这个角度来说，非线荷载获取抗拉强度的方法更为合理.

（3）线/非线荷载条件下各向同性部分（ISO）、纯双力偶（DC）和补偿线性矢量偶极成分（CLVD）的频率百分比，以及微裂纹破裂的主要类型所占比例对荷载条件并不敏感，两者破裂的机制均可以解释为近似平行于荷载方向上的张拉裂纹的萌生、扩展及贯通.